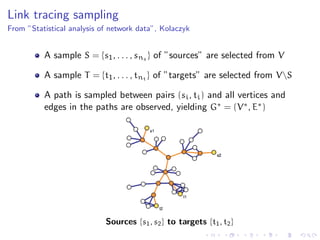
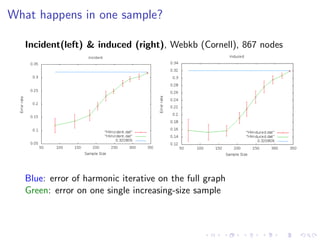
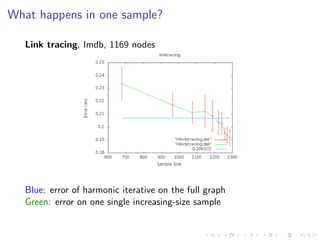
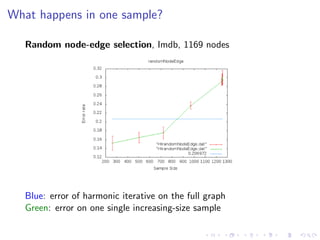
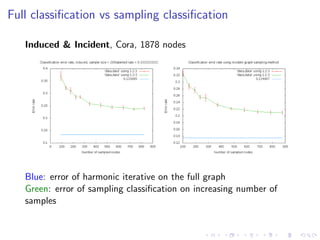
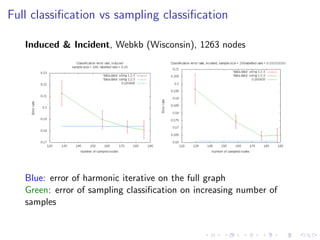
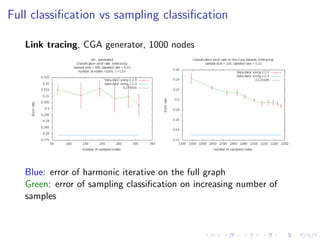
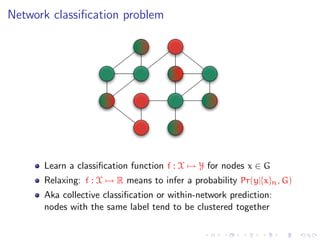
The document discusses the challenges of network classification, particularly the sparsity of labeled nodes and the impact of network structure on model accuracy. It introduces semi-supervised learning methods that leverage both labeled and unlabeled data through graph-based approaches, emphasizing harmonic functions and iterative methods for label propagation. Additionally, it explores sampling techniques to reduce complexity while approximating classifications within large graphs.

1. A discussion on sampling graphs to approximate
network classification functions
(work in progress)
Gemma C Garriga
INRIA
gemma.garriga@inria.fr
22.09.2011

2. Outline
Starting point
Classification in networks
Samples of graphs
Some first experiments

3. Outline
Starting point
Classification in networks
Samples of graphs
Some first experiments

4. Network classification problem
Learn a classification function f : X → Y for nodes x ∈ G
Relaxing: f : X → R means to infer a probability Pr(y|{x}n , G)
Aka collective classification or within-network prediction:
nodes with the same label tend to be clustered together

5. Network classification problem
Challenges
Sparsely labeled: few labeled nodes but many unlabeled nodes
Heterogeneous types of contents, multiple types of links
Network structure (what edges are in the graph) affects the
accuracy of the models
Networks are large size
Related to
Semi-supervised learning based on graphs

6. Semi-supervised learning
Goal
Build a learner f that can label input instances x into different
classes or categories y
Notation
input instance x, label y
learner f : X → Y
labeled data (Xl , Yl ) = {(x1:l , y1:l )}
unlabeled data Xu = {xl+1:n }, available during training
usually l n
Semi-supervised learning
Use both labeled and unlabeled data to build better learners

7. Semi-supervised graph-based methods
Transform vectorial data into a graph
Nodes: labeled and unlabeled Xl ∪ Xu
Edges: weighted edges (xi , xj ) computed from features
Weights represent similarity, e.g. wi,j = exp(−γ||xi − xj ||2 )
Sparsify with: k-nearest neighbor graph, threshold graph (
distance graph) . . .
The general idea is that there will be similiarity implied via all
paths in the graph

8. Semi-supervised graph-based methods
Smoothness assumption
In a weighted graph, nodes that are similar are connected by heavy
edges (high density region) and therefore tend to have the same
label. Density is not uniform
[From Zhu et al. ICML 2003]

9. The harmonic function
Relaxing discrete labels to real values with f : X −→ R that
satisfies:
1 f(xi ) = yi for i = 1 . . . l
2 f minimizes the energy function
wij (f(xi ) − f(xj ))2
ij
3 it is the mean of the associated Gaussian random field
4 the harmonic property means
j∼i wij f(xj )
f(xi ) =
j∼i wij

10. Harmonic solution with iterative method
An iterative method as in self-training:
1 Set f(xi ) = yi for i = 1 . . . l and f(xj ) arbitrary for xj ∈ Xu
2 Repeat until convergence:
j∼i wij f(xj )
Set f(xi ) = wij
j∼i
Keep always f(Xl ) fixed

11. A random walk interpretation on directed graphs
wij
Randomly walk from node i to j with probability
k wik
The harmonic function tells about Pr(hit label 1 | start from i)
[From Zhu’s tutorial at ICML 2007]

12. Harmonic solution with graph Laplacian
Let W be the n × n weight matrix on Xl ∪ Xu
Symmetric and non-negative
n
Let diagonal degree matrix D: Dii = j=1 wij
Graph Laplacian is ∆ = D − W
The energy function can be rewritten:
min wij (f(xi ) − f(xj ))2 = min ft ∆f
f f
ij
Harmonic solution solves fu = −∆uu −1 ∆ul Yl
Complexity of O(n3 )

13. Outline
Starting point
Classification in networks
Samples of graphs
Some first experiments

14. Characteristics of network data
So, can one use semi-supervised learning based on graphs for
networks? Some reflections:
+ The smoothness assumption can be seen as a clustering assumption,
or community structure assumption
Groups of nodes that are similar tend to be more densely
connected between them than with the rest of the network
+ The laplacian matrix could help to integrate both vectorial and
structure of the network
− However, networks have scale free of the degree distributions
Structure of the links influences iterative propagation
− Networks can be very large

15. How to use graph samples
First idea:
1 For i = 1 . . . |samples| do:
ˆ
Extract graph sample Gi G from the full graph
ˆ ˆ
Apply harmonic iterative algorithm to Gi to get f(u), u ∈ Gi
2 ˆ
Average f(u) for u ∈ {Gi } selected in several samples
3 For all nodes v that did appear in any sample do:
Make random walks to k nodes touched by samples
Compute weighted average of the k labels found
1
f(v) = d(v, uj )f(uj )
j={1...k} d(v, uj )
j={1...k}

16. How can samples help?
Samples have less edges than the full graph, so diffusion is different
from the full graph
Subgraphs will be random, so maybe a good behavior on average
The iterative algorithm (or laplacian harmonic) will be applied only
on samples. Complexity is reduced
The nodes not contained in any sample, will be labeled following
the assumptions of the random walk interpretation given by the
harmonic iterative solution
[From Zhu’s tutorial at ICML 2007]

17. How cannot samples help?
It depends on how samples in the graph are extracted. Things
to take into account
Including some labeled points from all classes in the sampled
graph
Extracting a connected subgraph
Sampling on the vectorial data, on the structural edges, or
integrating both in the sampling process (like random walk
sampling)
It is just an approximation, how good is it? can we say
something theoretically? ensemble approaches based on
samples?

18. Going further: sparsify the samples
Finding some sort of ”backbone”
Second idea:
1 For i = 1 . . . |samples| do:
ˆ
Extract graph sample Gi G from the full graph
ˆ ˆ
Apply harmonic iterative algorithm to Gi to obtain f(u), u ∈ Gi
2 ˆ
From S = {Gi } find nodes (or subgraph) U S with |U| = l s.t.
f(U ) = g(f(U))
where U = SU and g is some defined (linear) transformation
3 Label any other node v by k random walks to nodes in the
previous central nodes (or subgraph) U

19. Outline
Starting point
Classification in networks
Samples of graphs
Some first experiments

20. Induced subgraph sampling
From ”Statistical analysis of network data”, Kolaczyk
Sample n vertices without replacement to form
V ∗ = {i1 , . . . , in }
Edges are observed for vertex pairs i, j ∈ V ∗ for which
{i, j} ∈ E, yielding E∗
Selected nodes in yellow, observed edges in orange

21. Incident subgraph sampling
From ”Statistical analysis of network data”, Kolaczyk
Select n edges with random sampling without replacement, E∗
All incident vertices to E∗ are then observed, providing V ∗
Selected edges in yellow, observed nodes in orange

22. Star and snowball sampling
From ”Statistical analysis of network data”, Kolaczyk
∗
Take initial vertex sample V0 without replacement of size n.
Observe all edges incident to i ∈ V0 , yielding E∗
∗
∗
For labeled star sampling we observe also vertices i ∈ VV0 to
∗
which edges in E are incident
For snowball sampling we iterate the process of labeled star
sampling to neighbors up to the k-th wave
1-wave: yellow, 2-wave: orange, 3-wave: red

23. Link tracing sampling
From ”Statistical analysis of network data”, Kolaczyk
A sample S = {s1 , . . . , sns } of ”sources” are selected from V
A sample T = {t1 , . . . , tnt } of ”targets” are selected from VS
A path is sampled between pairs (si , ti ) and all vertices and
edges in the paths are observed, yielding G∗ = (V ∗ , E∗ )
Sources {s1 , s2 } to targets {t1 , t2 }

24. Some other sampling algorithms
Other possible ideas of sampling algorithms for graphs:
Random node selection, random edge selection
Selecting nodes with probability proportional to ”page rank”
weight
Random node neighbor
Random walk sampling
Random jump sampling
Forest fire sampling

25. Some challenges of sampling with labels
Including labels in the samples
Size of the samples
Isolated nodes
Edges of structure or content

26. Outline
Starting point
Classification in networks
Samples of graphs
Some first experiments

27. Experimental set-up
Classification algorithm
In the samples, compute the harmonic function f in iterative
fashion for ≈ 10 iterations
Final classification: for every node u assign label l that has
max value (probability) f(u)
Keep 1/3 of the labels
Datasets
Graph generated data: (1) cluster generator and (2)
community guided attachment generator
Other: Webkb, IMDB, Cora

28. What happens in one sample?
Incident(left) & induced (right), Webkb (Cornell), 867 nodes
Blue: error of harmonic iterative on the full graph
Green: error on one single increasing-size sample

29. What happens in one sample?
Link tracing, Imdb, 1169 nodes
Blue: error of harmonic iterative on the full graph
Green: error on one single increasing-size sample

30. What happens in one sample?
Random node-edge selection, Imdb, 1169 nodes
Blue: error of harmonic iterative on the full graph
Green: error on one single increasing-size sample

31. Full classification vs sampling classification
Induced & Incident, Cora, 1878 nodes
Blue: error of harmonic iterative on the full graph
Green: error of sampling classification on increasing number of
samples

32. Full classification vs sampling classification
Induced & Incident, Webkb (Wisconsin), 1263 nodes
Blue: error of harmonic iterative on the full graph
Green: error of sampling classification on increasing number of
samples

33. Full classification vs sampling classification
Link tracing, CGA generator, 1000 nodes
Blue: error of harmonic iterative on the full graph
Green: error of sampling classification on increasing number of
samples

34. Some discussion
Samples of graphs can serve to avoid high complexity (O(n3 ))
of applying learning algorithm in the full graph
Choice of sampling methods (e.g. snowball is bad for highly
connected graphs, link tracing is useful in highly clustered
graphs)
Approximation of accuracy is reasonable with small number of
samples already
Question of the I/O operations in the graph
Samples of the graph to estimate a distribution?
Ensemble approaches?
Approximation in terms of shortest paths?