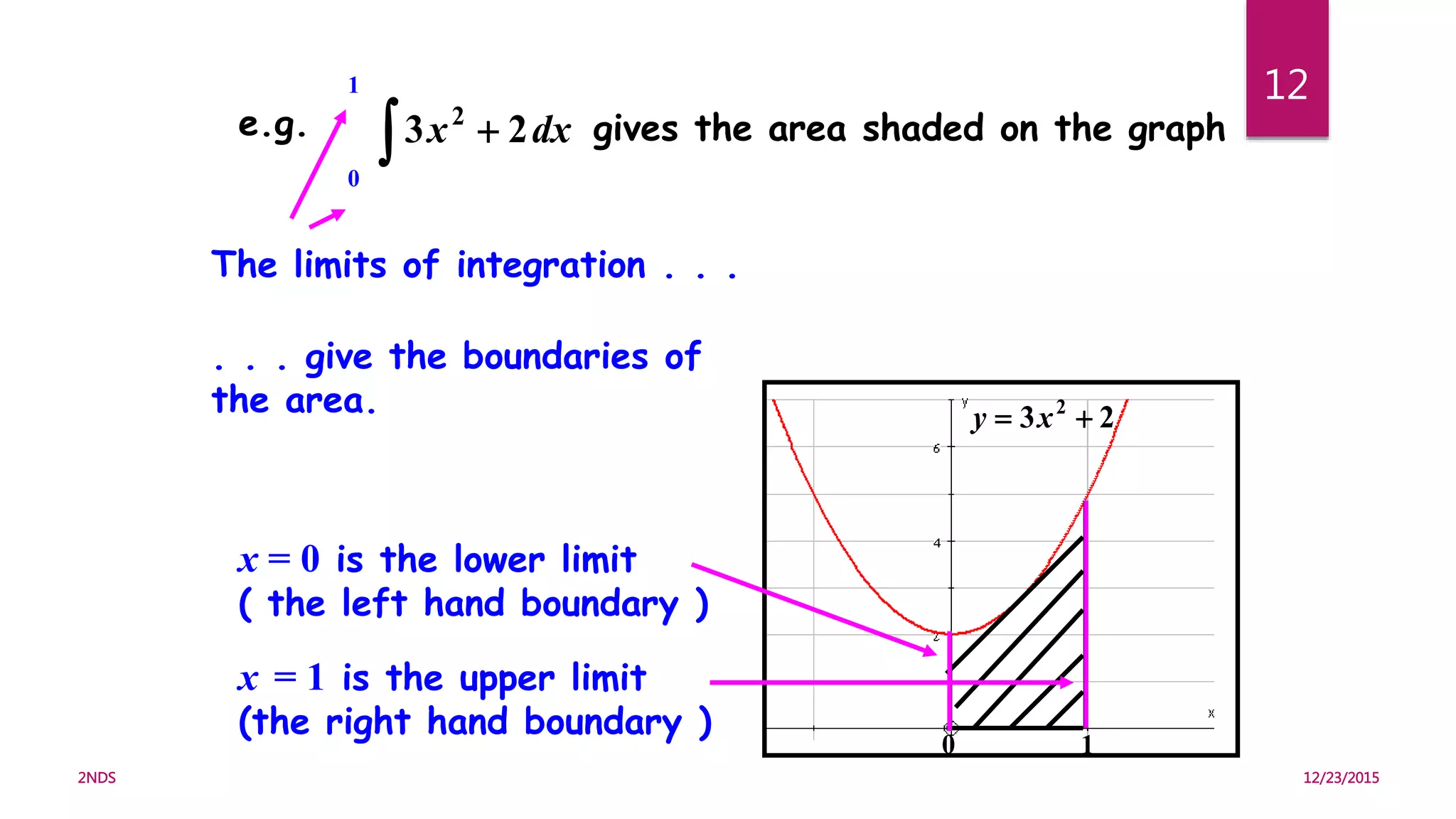
- Calculus involves dividing problems into small pieces to understand change (differential calculus) or combining pieces to find totals (integral calculus). - Newton's Law of Cooling uses differential calculus to model how an object's temperature changes over time as it approaches the temperature of its environment. - Integral calculus can be used to calculate the area under a curve, such as finding the area between a curve and the x-axis given the curve's equation and bounds of integration.

1. Calculus In Real Life
“nothing takes place in the world whose meaning
is not that of some maximum or minimum.”
--leonhard euler
1

2. What is calculus ?
12/23/20152NDS
2
 The word Calculus comes from Latin meaning "small stone",
Because it is like understanding something by looking at small pieces.
 Derived from the Latin “calx” (counter) – ancient Babylonians would use pebbles to represent
units, tens, hundreds, etc, on a primitive abacus.
 Later, defined as measuring varying rates of change.

3. Calculus is everywhere
The differentiation and integration of calculus have many
real-world applications from sports to engineering to astronomy and space travel.
12/23/20152NDS
3

4. Types of Calculus
12/23/20152NDS
4
• Differential Calculus cuts something into small pieces to find how it
changes.
• Integral Calculus joins (integrates) the small pieces together to find how
much there is.

5. Differential Calculus
Newton’s Law of Cooling
 Newton’s observations:
He observed that observed that the temperature of the body is proportional to the difference
between its own temperature and the temperature of the objects in contact with it .
 Formulating:
First order separable DE
 Applying calculus:
𝑑𝑇
𝑑𝑡
= −𝑘(𝑇 − 𝑇𝑒)
Where k is the positive proportionality constant
12/23/20152NDS
5

6. Applications on Newton’s Law of Cooling:
Investigations.
• It can be used to
determine the
time of death.
Computer
manufacturing.
• Processors.
• Cooling systems.
solar water
heater.
calculating the
surface area of
an object.
12/23/20152NDS
6

7. Calculate Time of Death
12/23/20152NDS
7
The police came to a house at 10:23 am were a murder had
taken place. The detective measured the temperature of the
victim’s body and found that it was 26.7℃. Then he used a
thermostat to measure the temperature of the room that
was found to be 20℃ through the last three days. After an
hour he measured the temperature of the body again and
found that the temperature was 25.8℃. Assuming that the
body temperature was normal (37℃), what is the time of
death?

8. Solution
12/23/20152NDS
8
T (t) = Te + (T0 − Te ) e – kt
Let the time at which the death took place be x hours before the arrival
of the police men.
Substitute by the given values
T ( x ) = 26.7 = 20 + (37 − 20) e-kx
T ( x+1) = 25.8 = 20 + (37 − 20) e - k ( x + 1)
Solve the 2 equations simultaneously
0.394= e-kx
0.341= e - k ( x + 1)
By taking the logarithmic function
ln (0.394)= -kx …(1)
ln (0.341)= -k(x+1) …(2)

9. Result
By dividing (1) by (2)
ln(0.394)
ln 0.341
=
−𝑘𝑥
−𝑘 𝑥+1
0.8657 =
𝑥
𝑥+1
Thus x≃7 hours
Therefore the murder took place 7 hours before the arrival of the detective which is at
3:23 pm
12/23/20152NDS
9

10. Computer Processor Manufacture
 A global company such as Intel is willing to produce a new cooling system for their
processors that can cool the processors from a temperature of 50℃ to 27℃ in just half
an hour when the temperature outside is 20℃ but they don’t know what kind of
materials they should use or what the surface area and the geometry of the shape are.
So what should they do ?
 Simply they have to use the general formula of Newton’s law of cooling
 T (t) = Te + (T0 − Te ) e– k
 And by substituting the numbers they get
 27 = 20 + (50 − 20) e-0.5k
 Solving for k we get k =2.9
 so they need a material with k=2.9 (k is a constant that is related to the heat capacity ,
thermodynamics of the material and also the shape and the geometry of the material)
12/23/20152NDS
10

11. It can be used to find an area bounded, in
part, by a curve
Integral Calculus
12/23/20152NDS
11

12. . . . give the boundaries of
the area.
The limits of integration . . .
0 1
23 2
 xy
x = 0 is the lower limit
( the left hand boundary )
x = 1 is the upper limit
(the right hand boundary )
  dxx 23 2
0
1
e.g. gives the area shaded on the graph
12/23/20152NDS
12

13. 0 1
23 2
 xy
the shaded area equals 3
The units are usually unknown in this type of question
 
1
0
2
23 dxxSince
3
1
0



 xx 23

Finding and Area
12/23/20152NDS
13

14. SUMMARY
• the curve ),(xfy 
• the lines x = a and x = b
• the x-axis and
PROVIDED that
the curve lies on, or above, the x-axis between
the values x = a and x = b
 The definite integral or
gives the area between

b
a
dxxf )(

b
a
dxy
12/23/20152NDS
14

15. • Business and politicians often conduct surveys with the help of calculus.
• Investment plans do not pass before mathematicians approves.
• Doctors often use calculus in the estimation of the progression of the illness.
• Global mapping is done with the help of calculus.
• Calculus also used to solve paradoxes.
Calculus in other fields
12/23/20152NDS
15

16. THANK YOU ALL…!!!
12/23/20152NDS
16