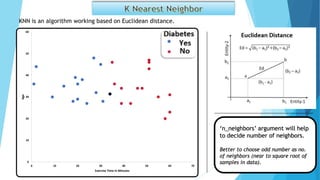
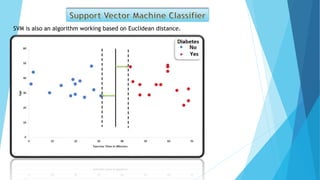
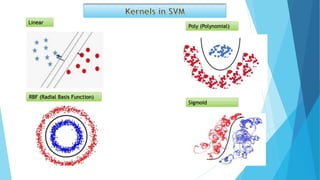
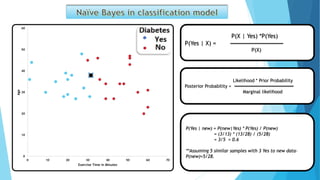
This document discusses several machine learning algorithms and concepts: KNN is a algorithm that uses Euclidean distance to determine the number of nearest neighbors based on the number of samples in the data. SVM and KNN both use Euclidean distance. Bayes' theorem is a formula for calculating conditional probability based on likelihood, prior probability, and posterior probability. An example shows how to apply Bayes' theorem to calculate the probability of a new data point being "Yes" given existing sample data.

2. 0
10
20
30
40
50
60
0 10 20 30 40 50 60 70
Age
Exercise Time in Minutes
‘n_neighbors’ argument will help
to decide number of neighbors.
Better to choose odd number as no.
of neighbors (near to square root of
samples in data).
KNN is an algorithm working based on Euclidean distance.

3. SVM is also an algorithm working based on Euclidean distance.

4. Linear
RBF (Radial Basis Function)
Poly (Polynomial)
Sigmoid

6.  P(A) – the probability of event A.
 P(B) – the probability of event B.
 P(A|B) – P(A), given event B has occurred.
 P(B|A) – P(B), given event A has occurred.
 Is a mathematical formula for determining conditional probability.
 Was named after mathematician Thomas Bayes.

7. Reference: https://www.mathsisfun.com/data/bayes-theorem.html

8. 0
10
20
30
40
50
60
0 10 20 30 40 50 60 70
Age
Exercise Time in Minutes
P(X | Yes) *P(Yes)
P(Yes | X) =
P(X)
Likelihood * Prior Probability
Posterior Probability =
Marginal likelihood
P(Yes | new) = P(new|Yes) * P(Yes) / P(new)
= (3/13) * (13/28) / (5/28)
= 3/5 = 0.6
**Assuming 5 similar samples with 3 Yes to new data-
P(new)=5/28.