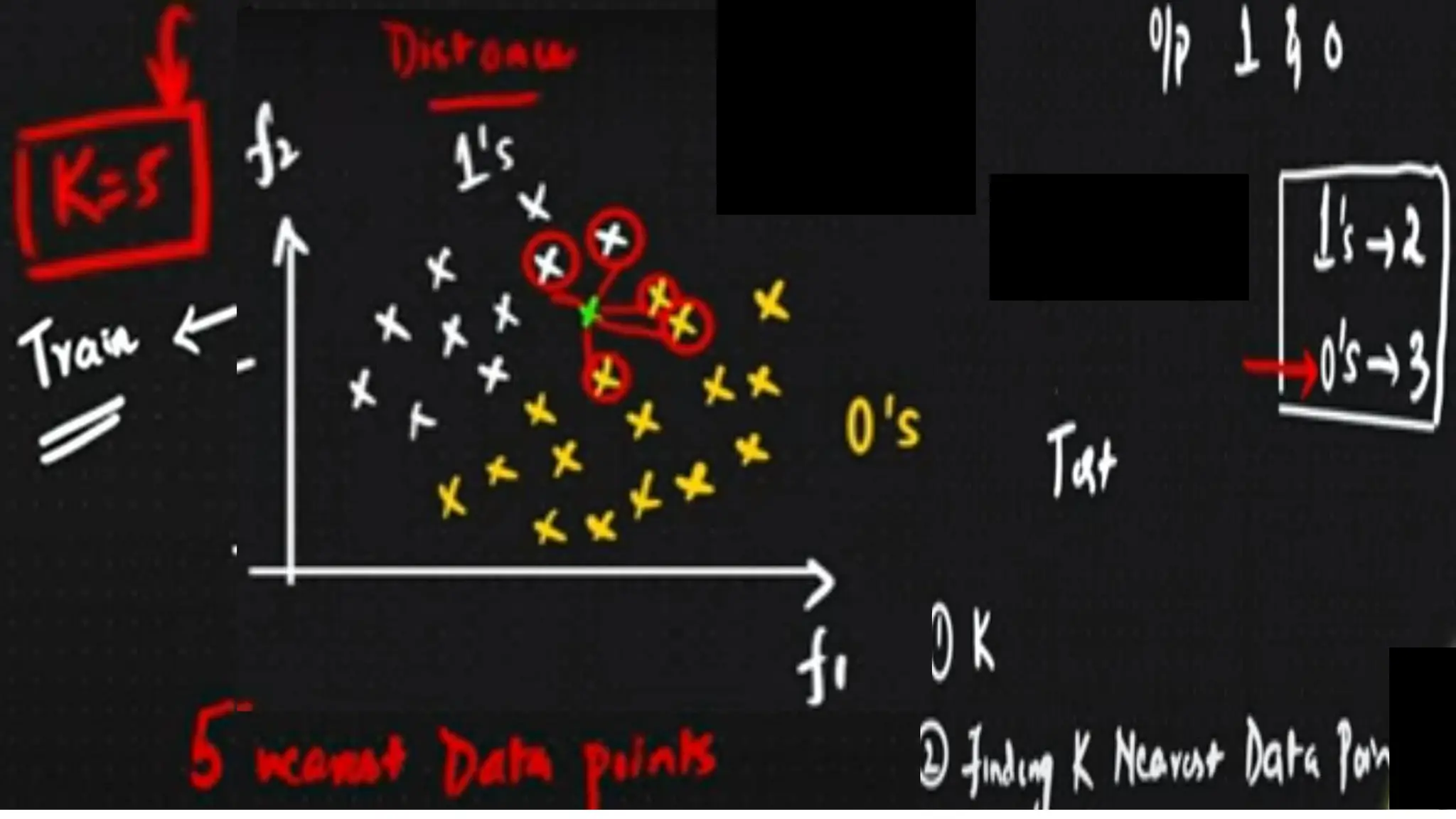
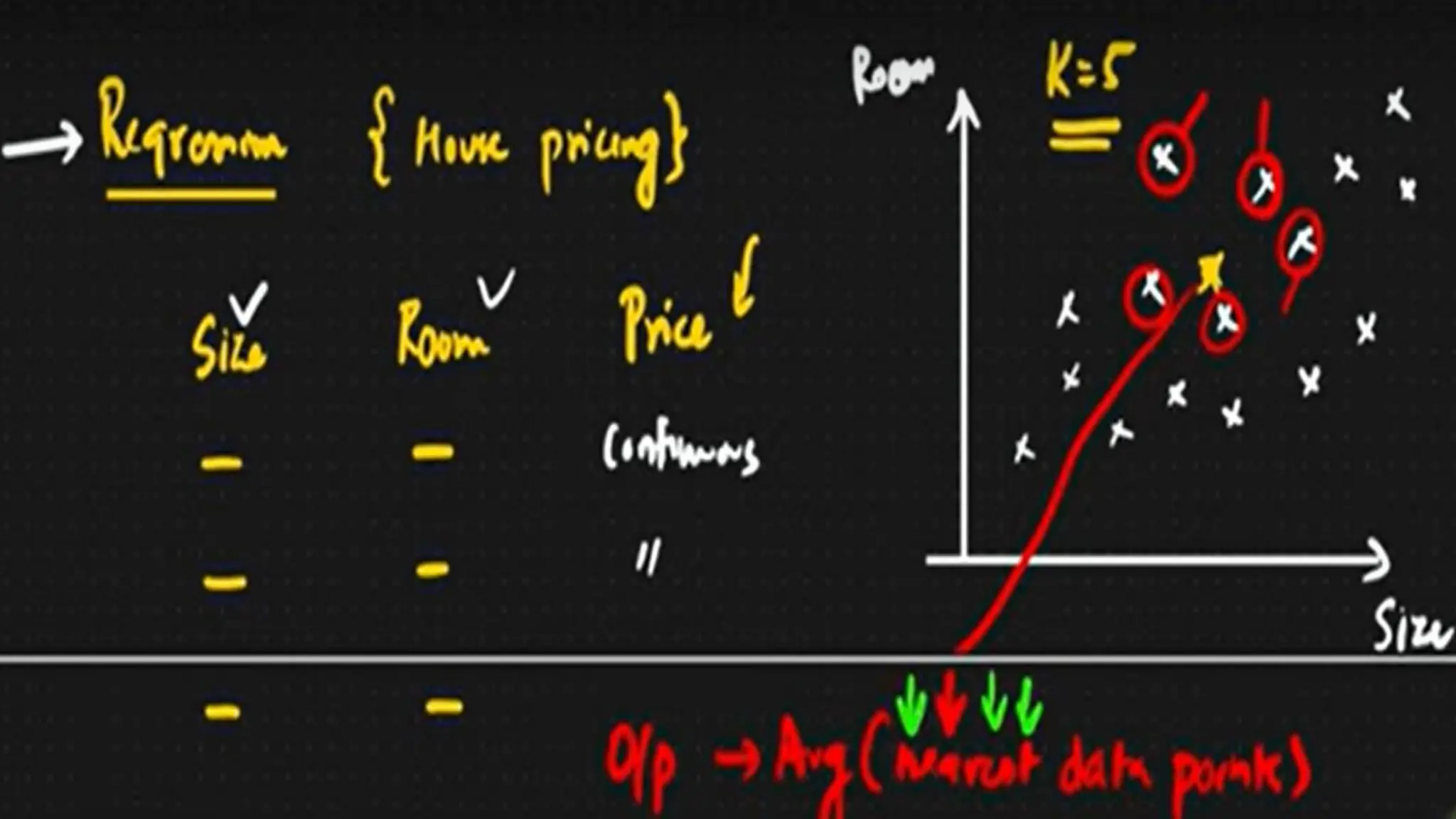
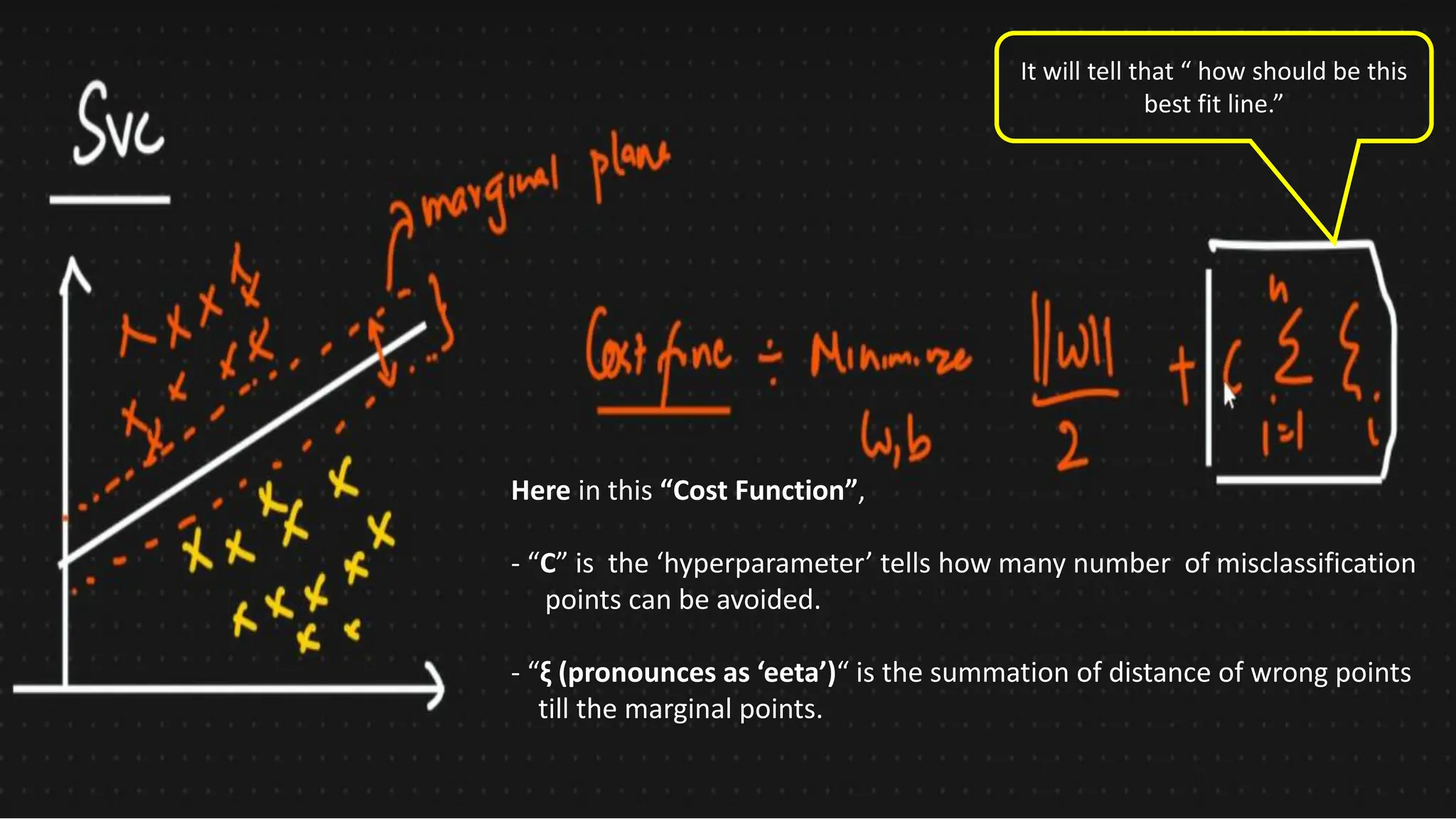
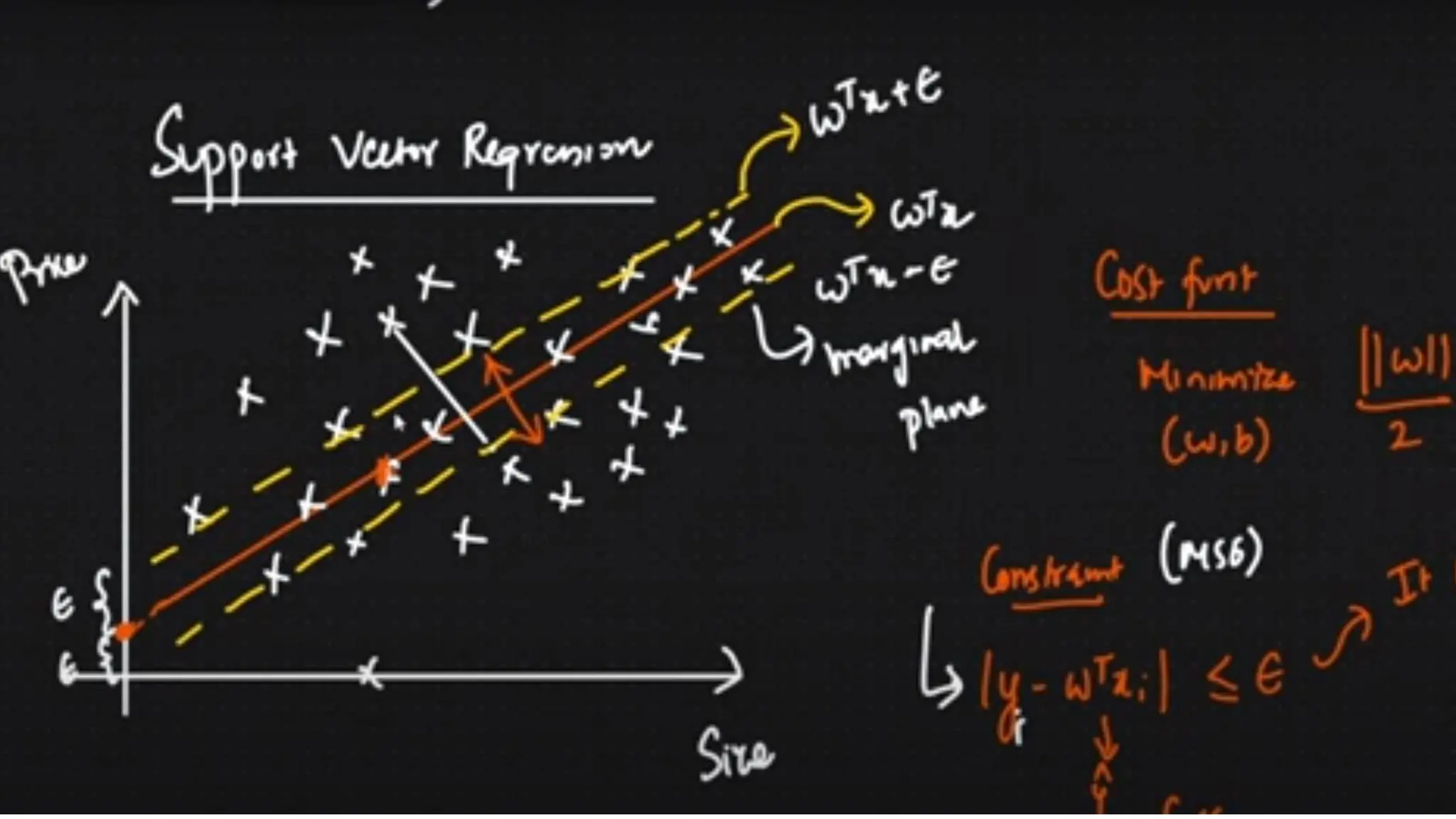
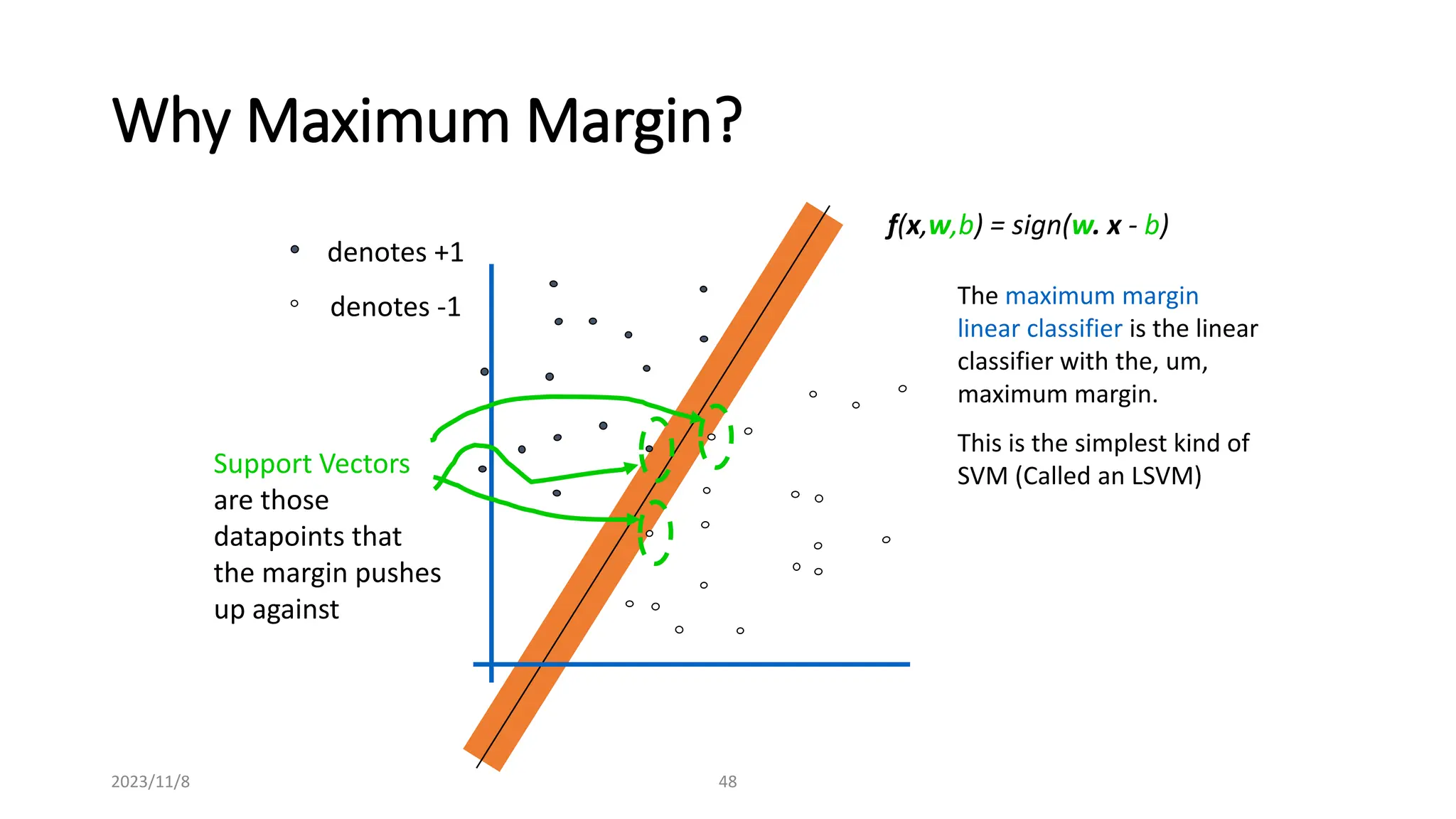
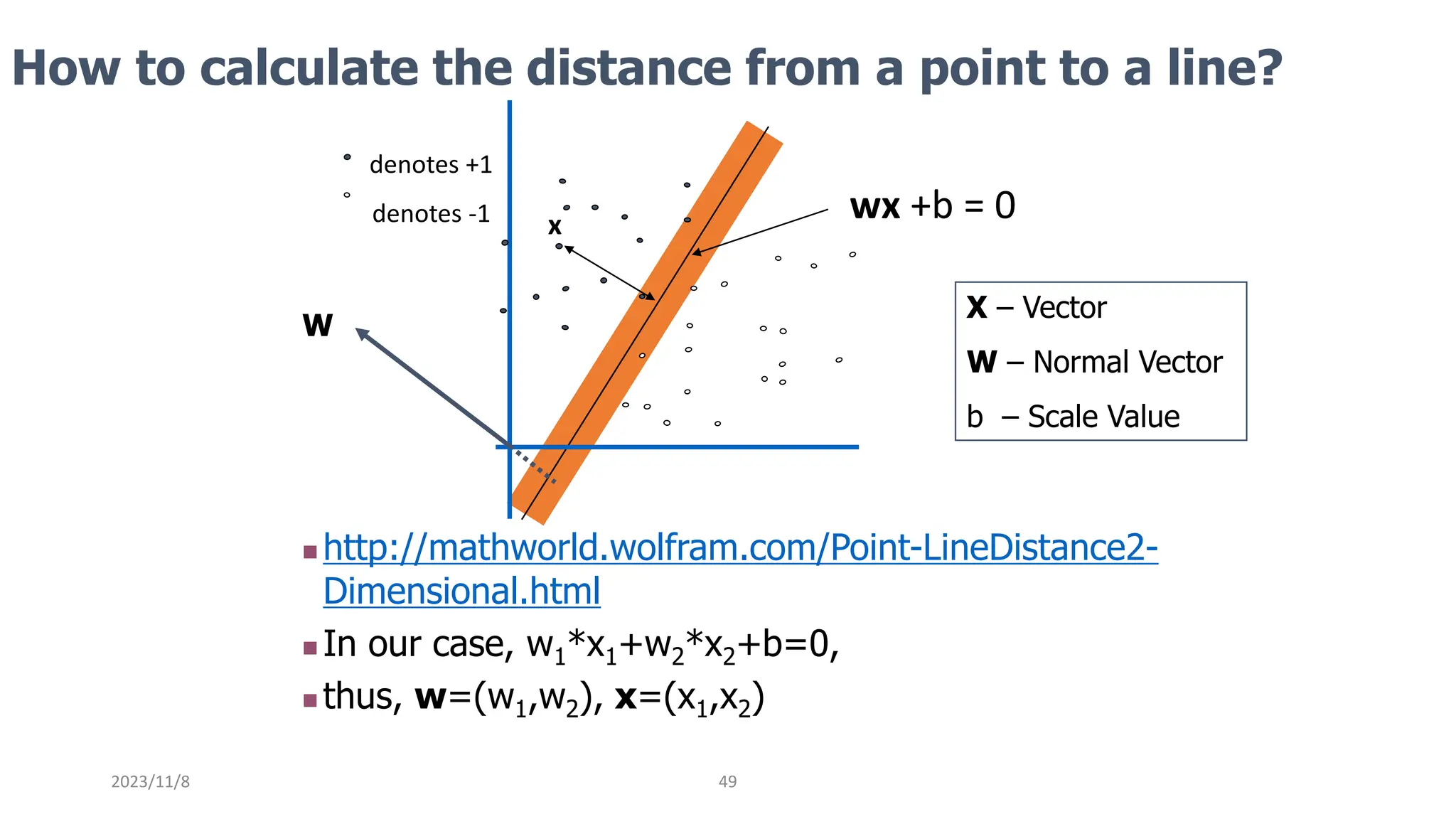
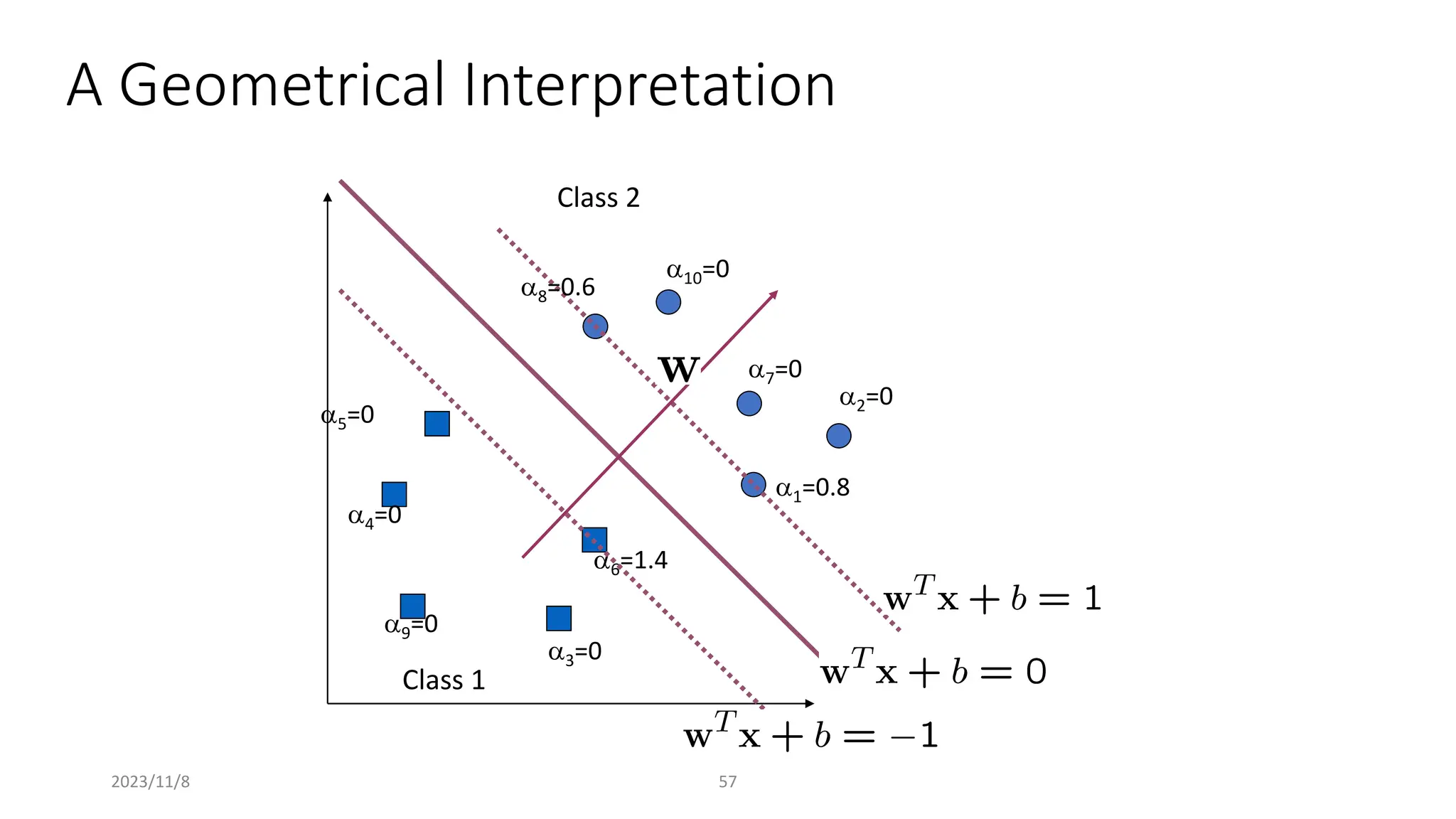
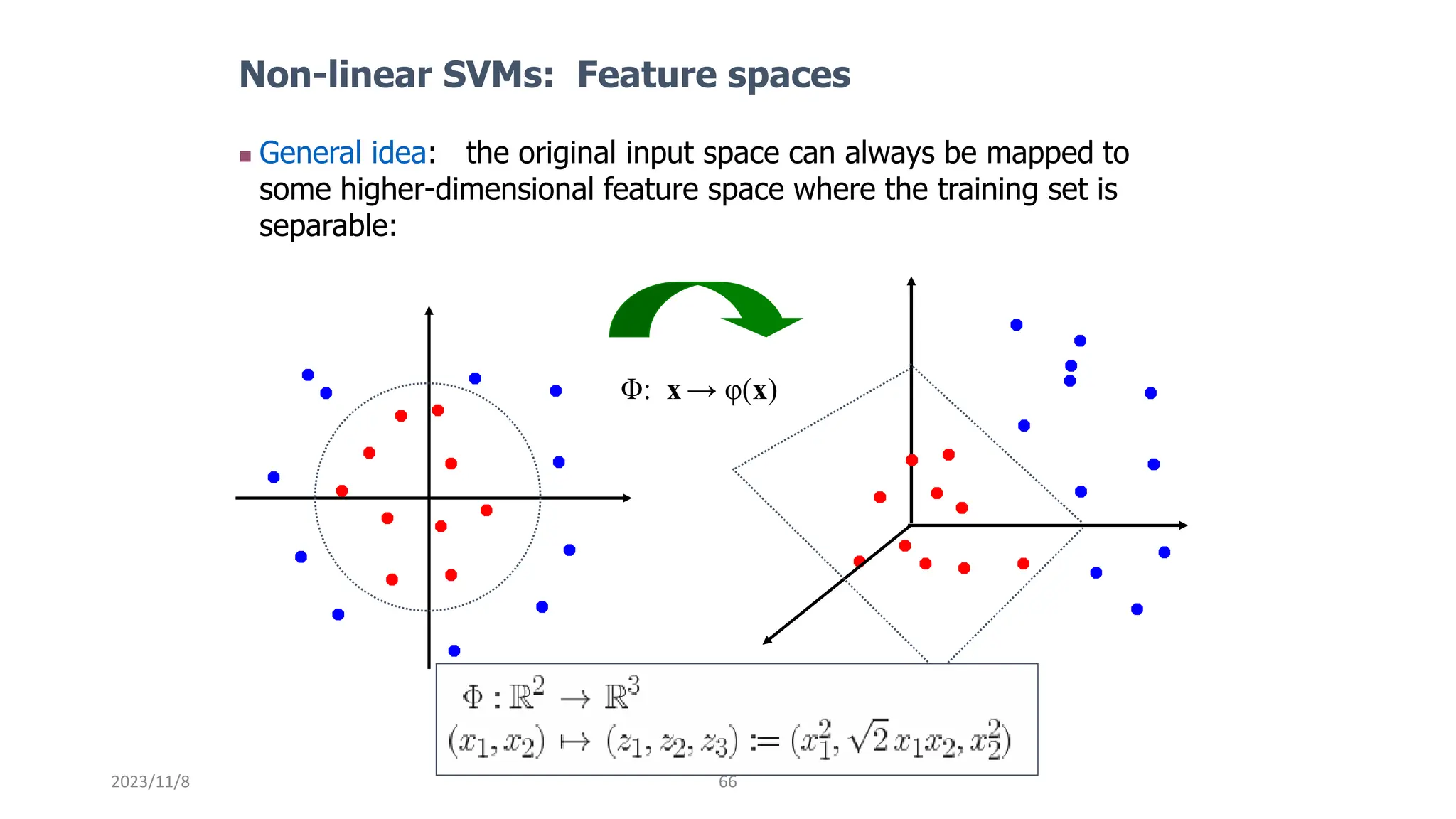
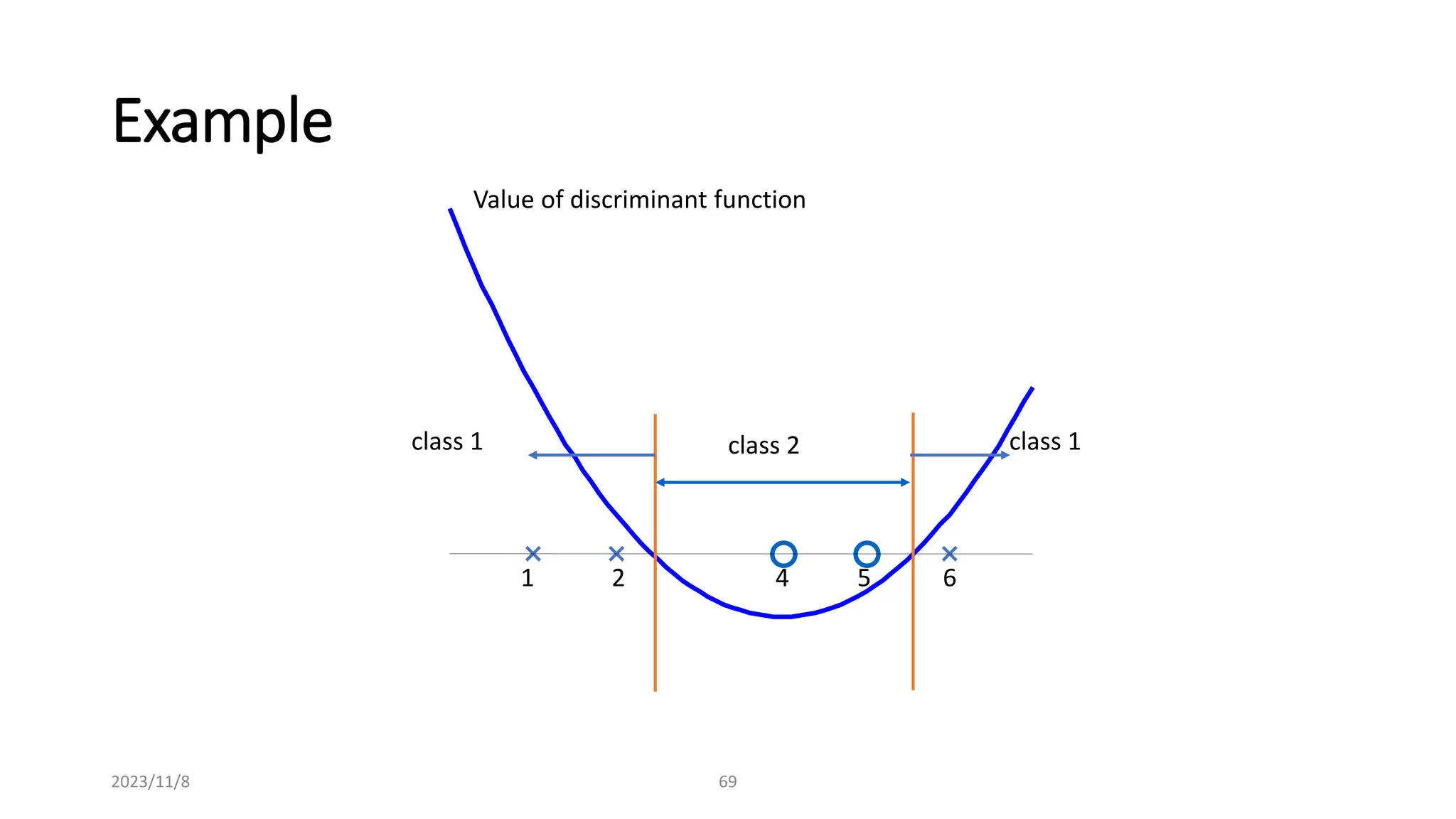
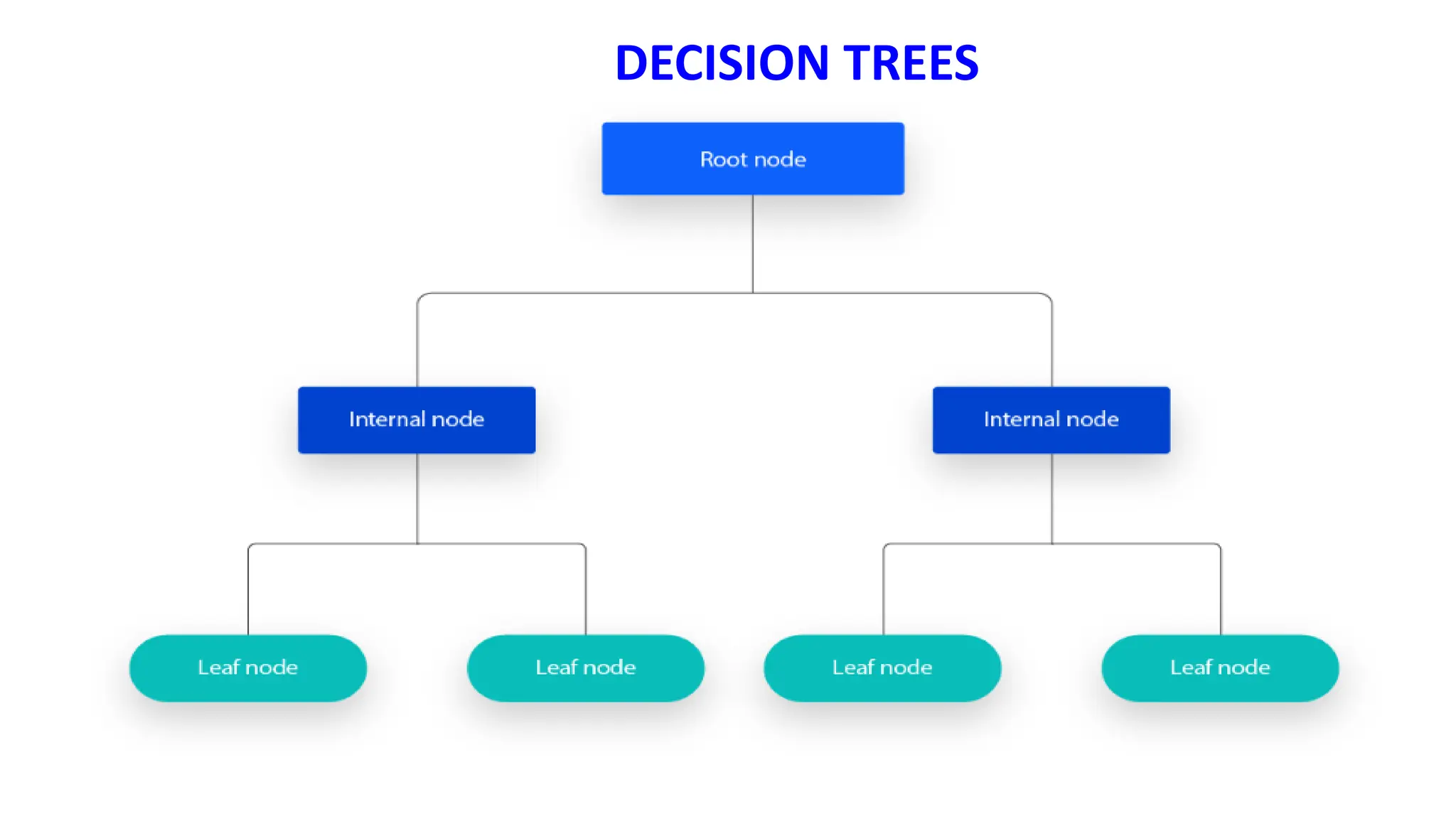
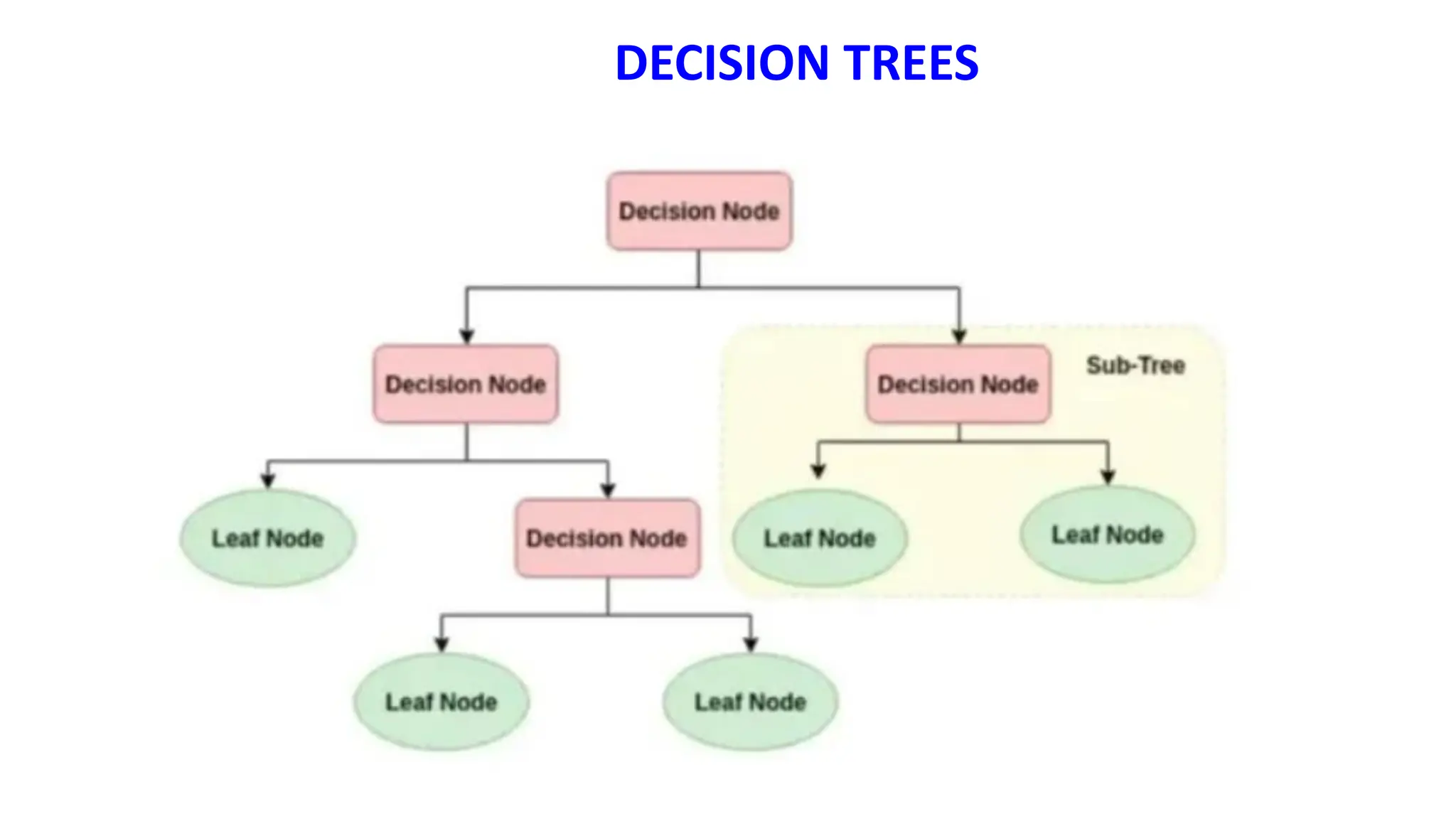
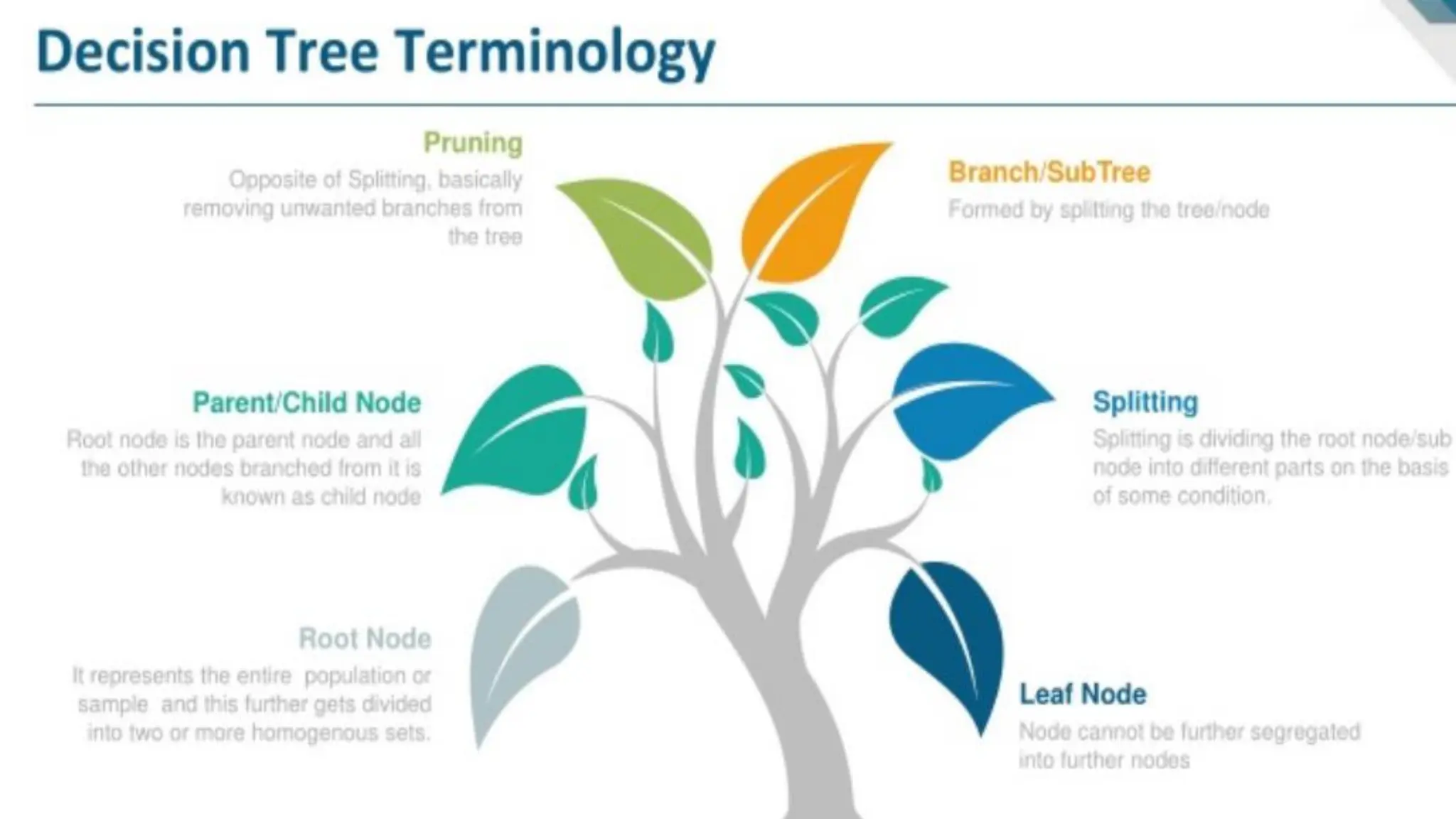
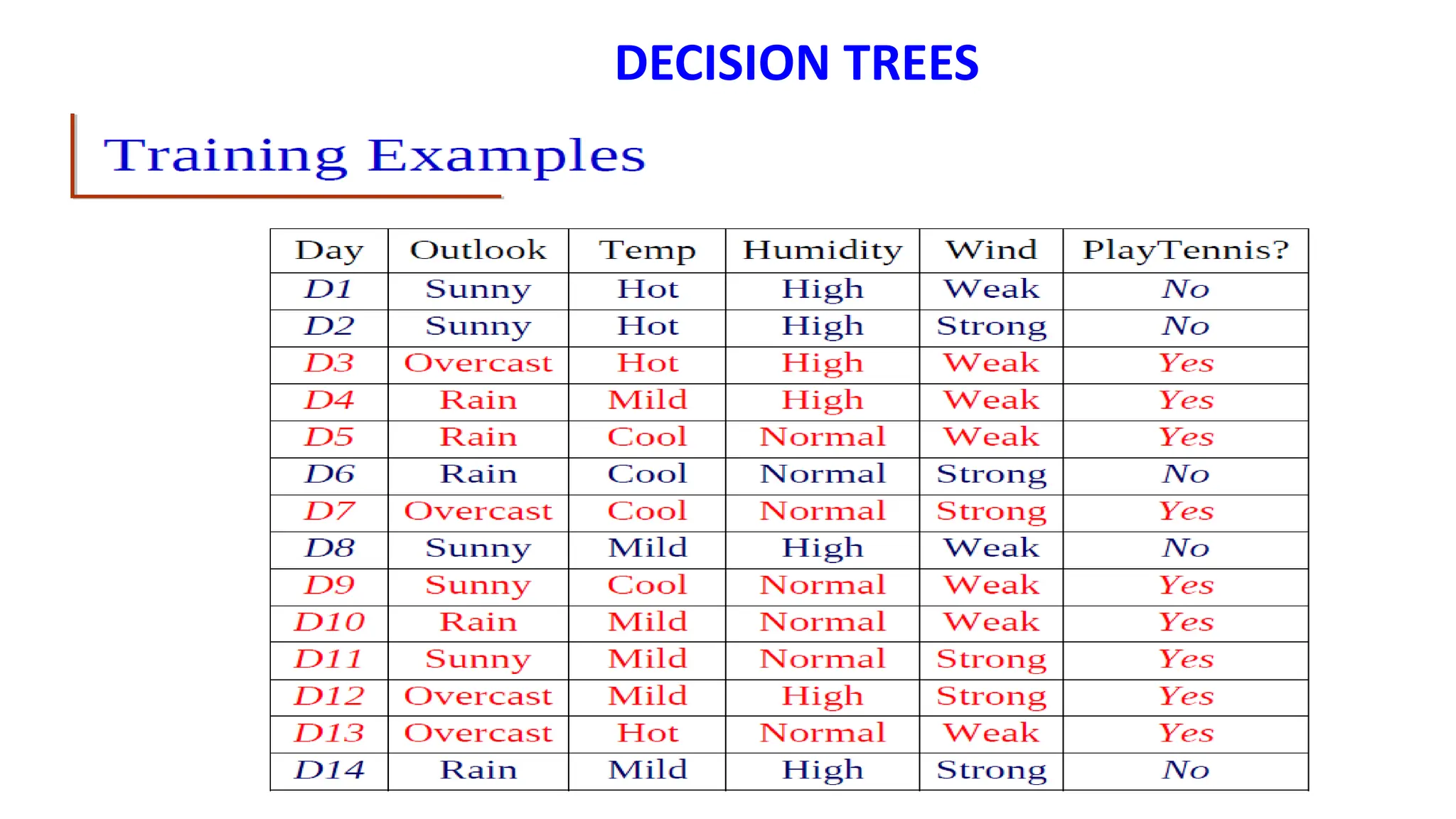
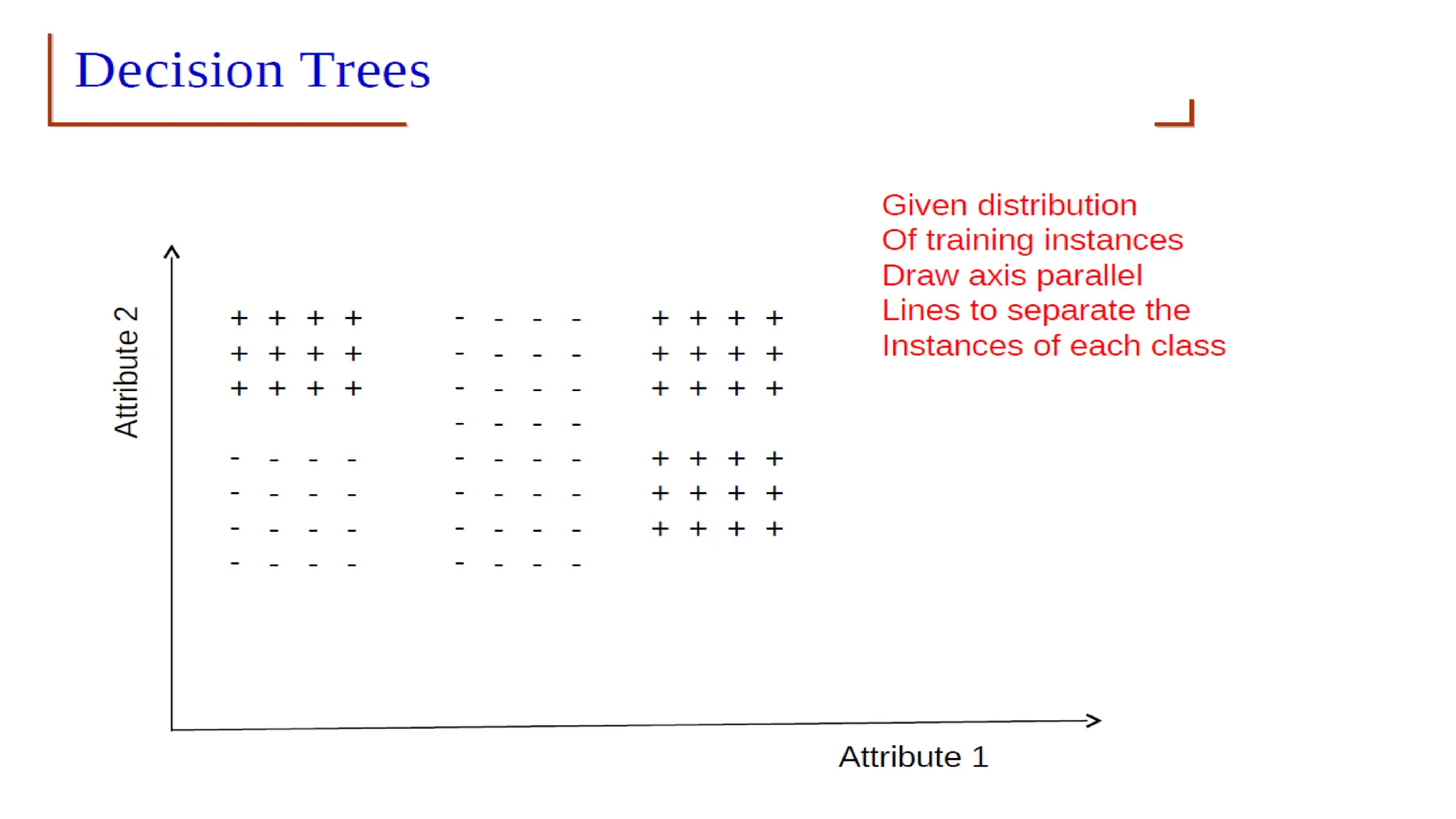
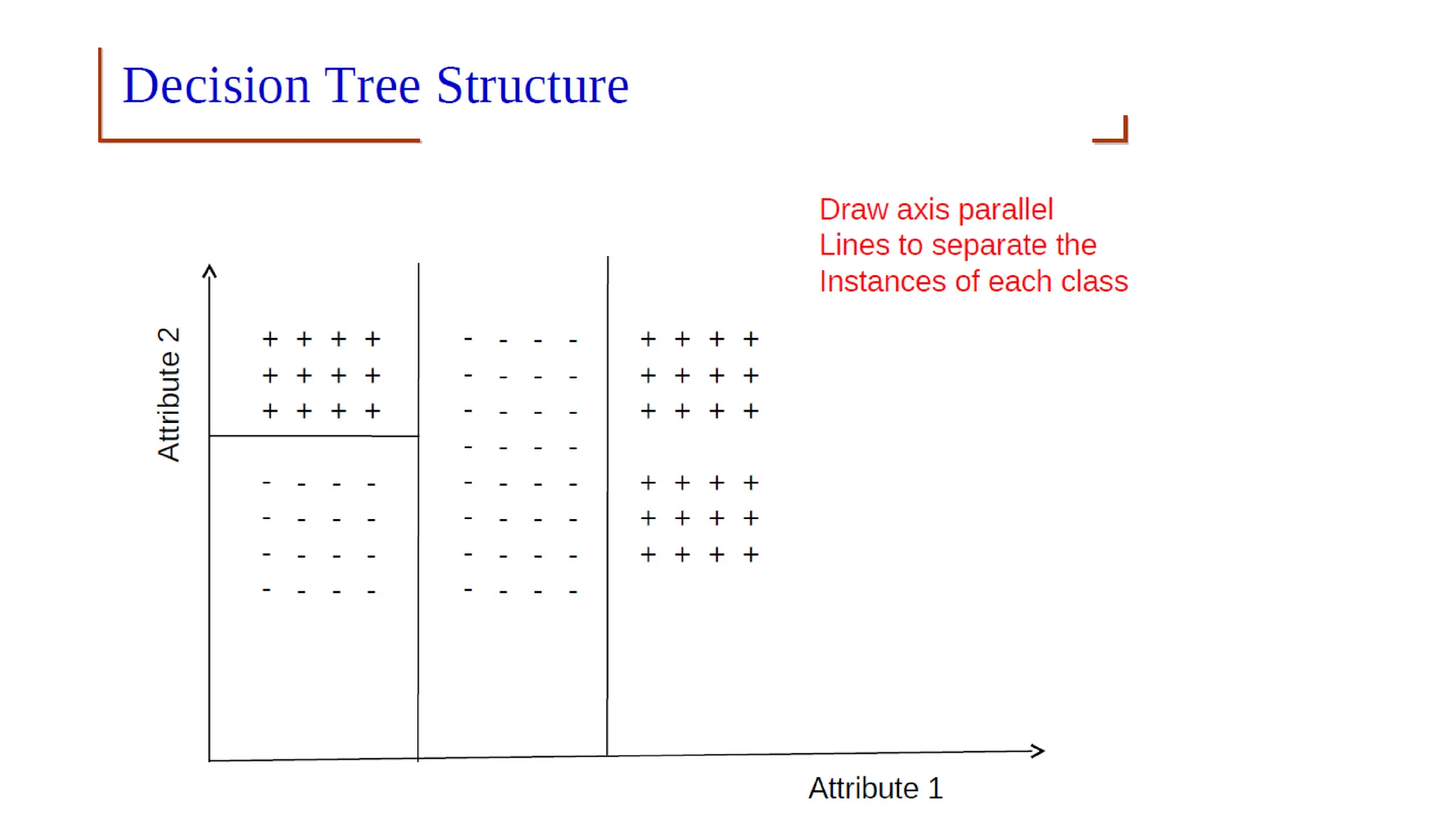
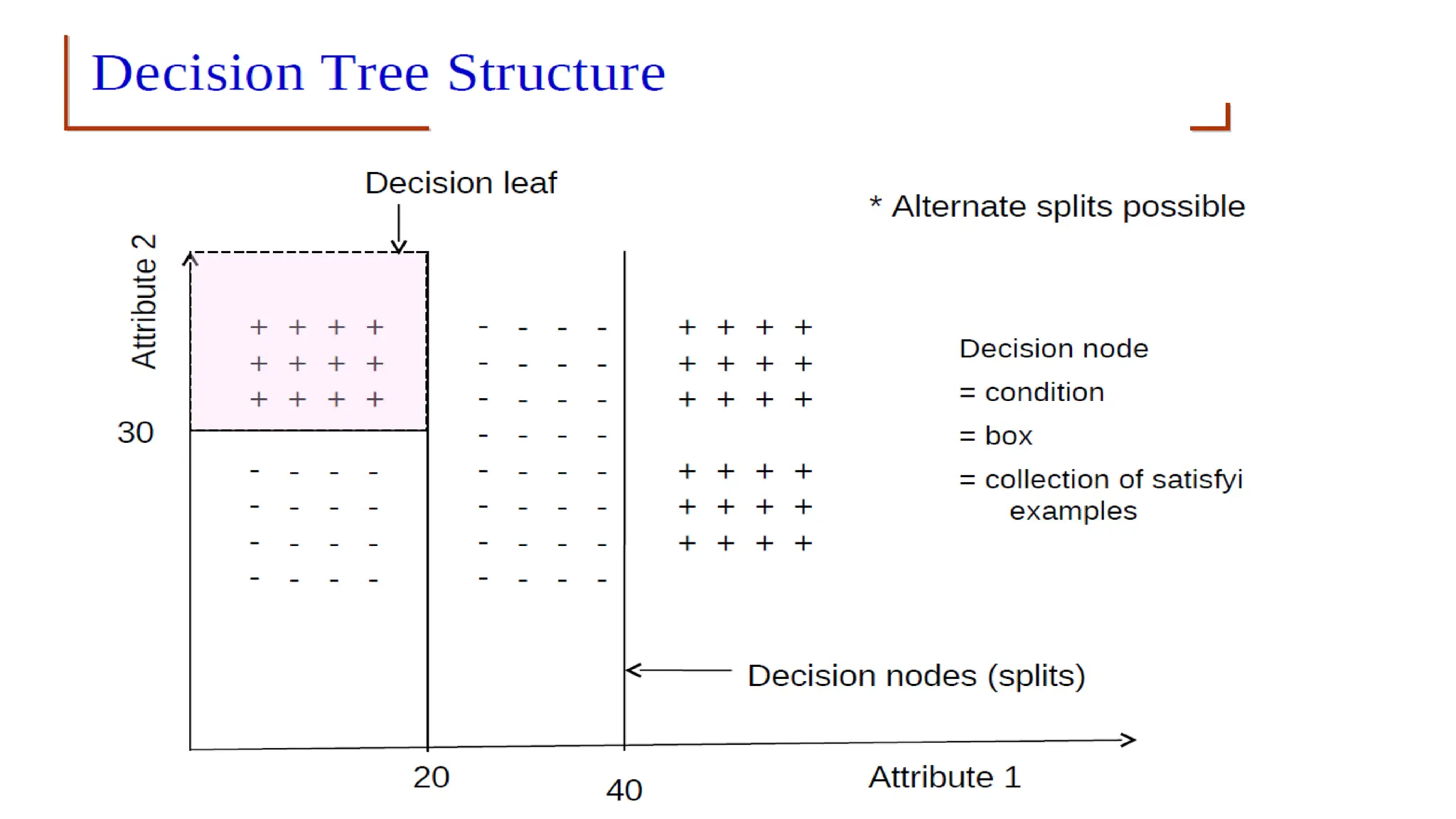
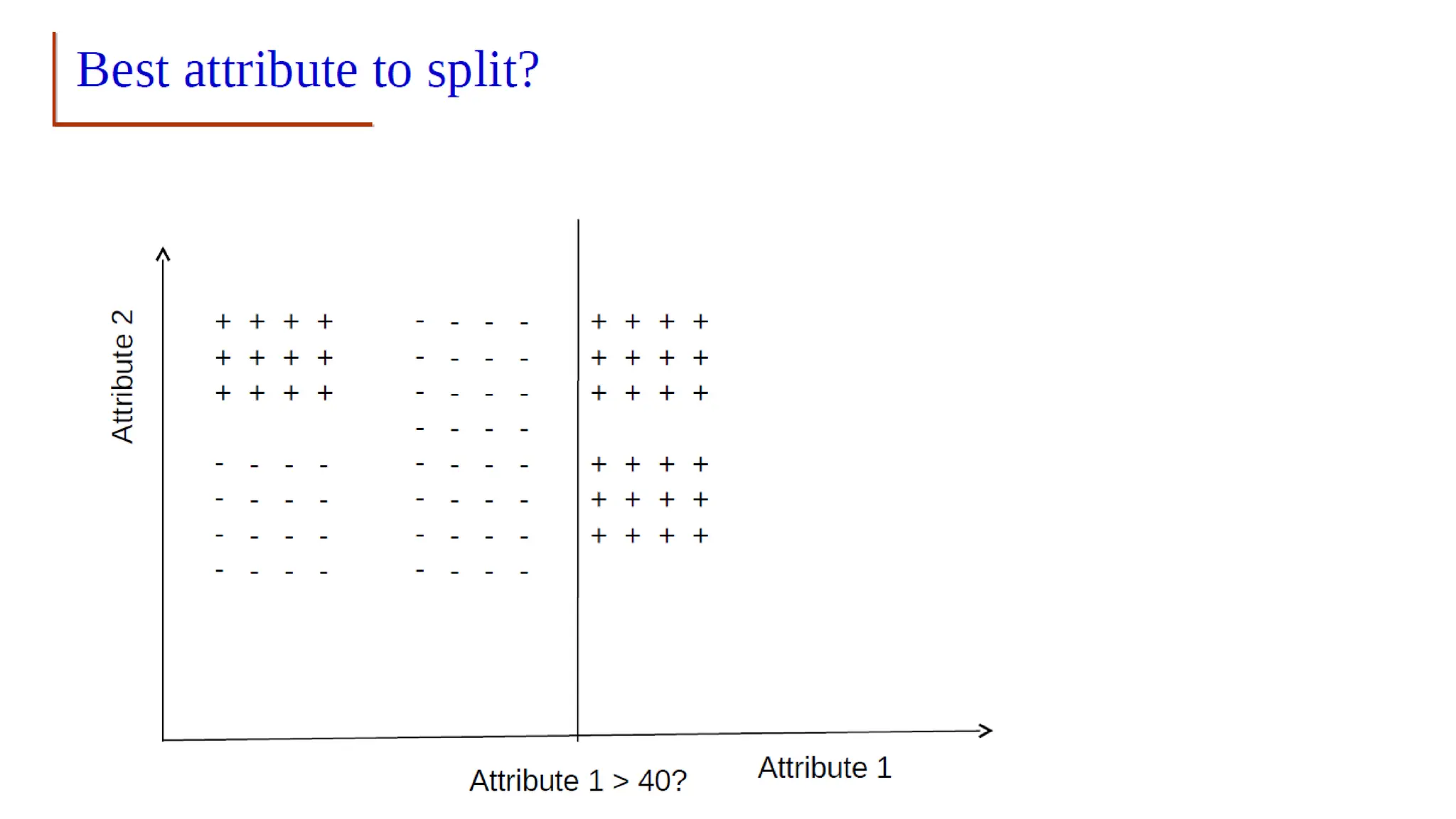
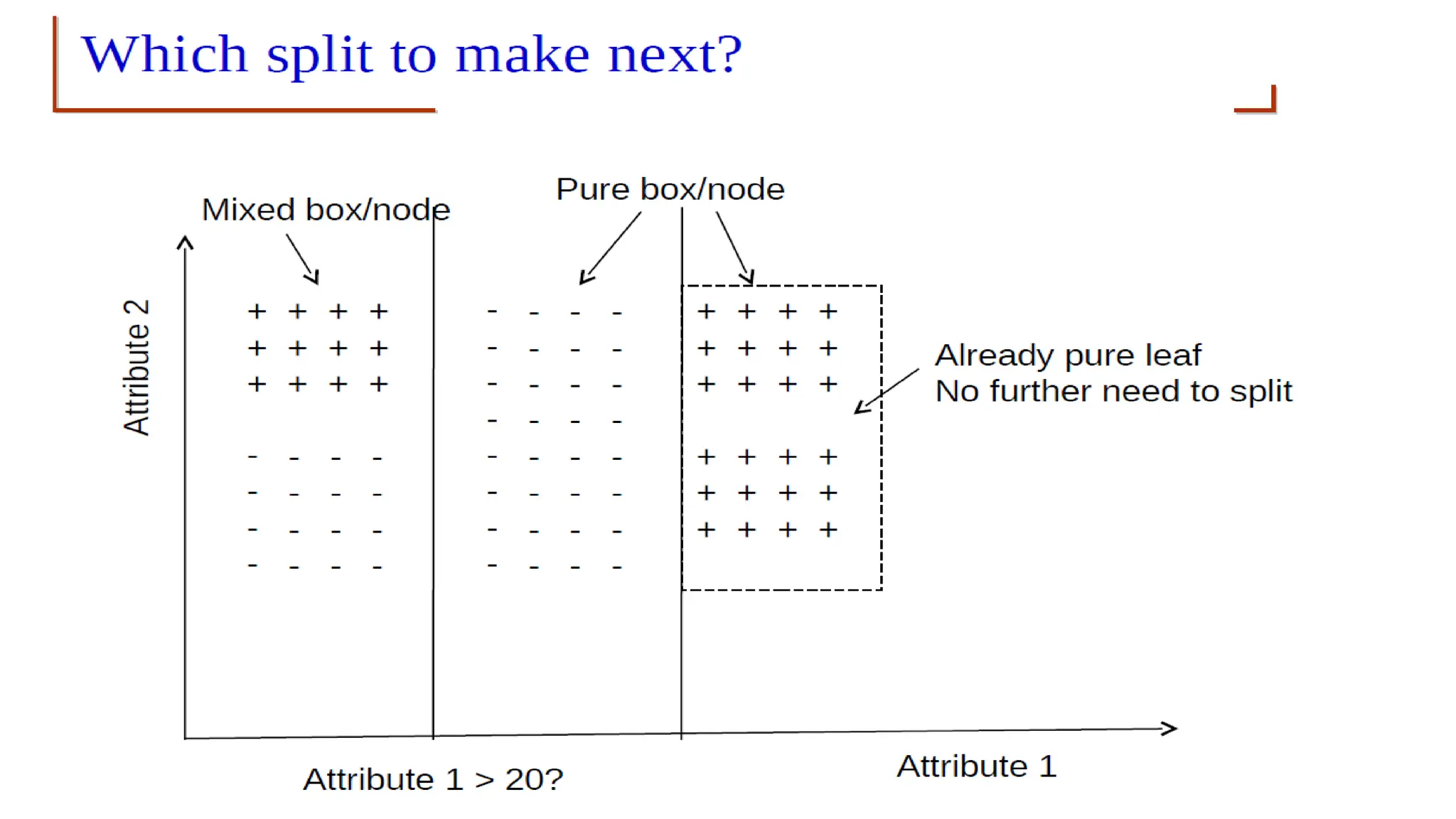
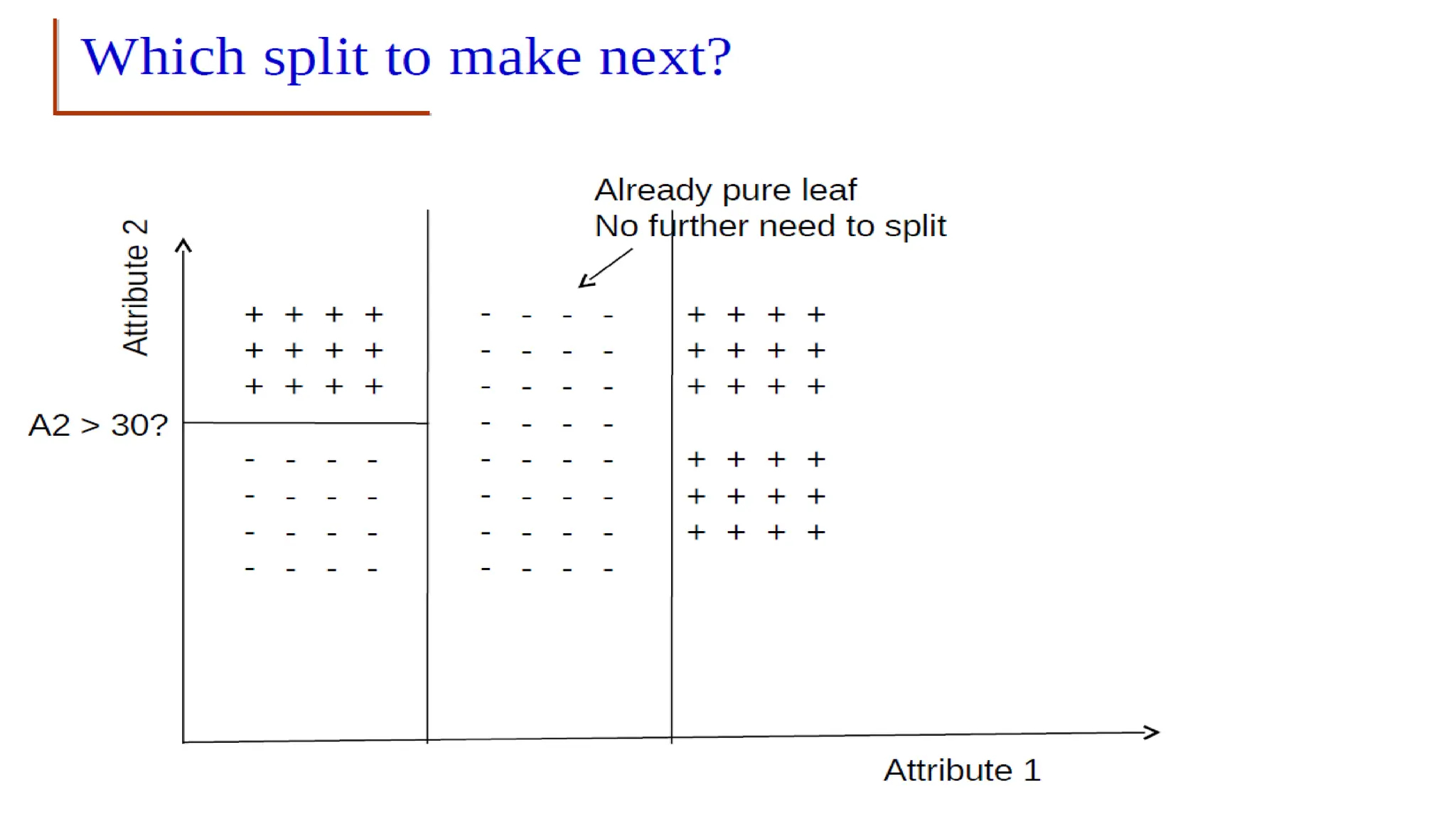
The document covers advanced topics in supervised learning, focusing on the k-nearest neighbors (KNN) algorithm and support vector machines (SVM). KNN is a non-parametric classifier that utilizes proximity for classification or regression based on majority voting and various distance metrics, while SVM is effective for binary and multi-class classification and regression, emphasizing the concept of maximizing the margin between classes. The limitations of KNN include scaling issues and susceptibility to noise, whereas SVM faces challenges with larger datasets and noise but is favored for its high accuracy on cleaner datasets.