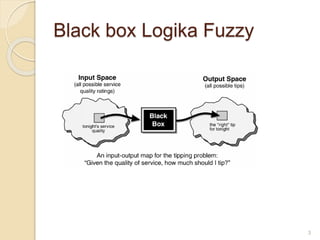
Dokumen ini membahas tentang logika fuzzy dalam kecerdasan buatan, menjelaskan konsep dasar, aplikasi, dan perbandingan dengan logika klasik. Logika fuzzy digunakan untuk menggambarkan ketidakjelasan dan memiliki aplikasi dalam berbagai bidang seperti pengendalian mesin, kedokteran, dan pengambilan keputusan. Metode inferensi fuzzy, termasuk Tsukamoto, digunakan untuk memodelkan dan menghitung hasil keputusan berdasarkan input yang fuzzy.





![Himpunan Crisp (tegas)
Nilai keanggotaan suatu item x dalam suatu himpunan A, ditulis
A[x], memiliki 2 kemungkinan:
◦ Satu (1): berarti bahwa suatu item menjadi anggota dalam suatu
himpunan, dan
◦ Nol (0): berarti bahwa suatu item tidak menjadi anggota dalam suatu
himpunan.
Contoh:
◦ S = {1, 2, 3, 4, 5} adalah semesta pembicaraan
◦ A = {1, 2, 3}
◦ B = {3, 4, 5}
Bisa dikatakan bahwa:
◦ Nilai keanggotaan 2 pada himpunan A, A[2]=1, karena 2 A
◦ Nilai keanggotaan 3 pada himpunan A, A[3]=1, karena 3 A
◦ Nilai keanggotaan 4 pada himpunan A, A[4]=0, karena 4 A
◦ Nilai keanggotaan 2 pada himpunan B, A[2]=0, karena 2 A
◦ Nilai keanggotaan 3 pada himpunan B, A[3]=1, karena 3 B
7](https://image.slidesharecdn.com/ai2011-5-logika-fuzzy1-230623123530-b4c6c712/85/Kecerdasan-Buatan-7-320.jpg)
![Himpunan Crisp (tegas) – Cont’d
Misal variable umur dibagi menjadi 3 katagori :
◦ MUDA umur <35 tahun
◦ PAROBAYA 35 ≤ umur ≤ 55 tahun
◦ TUA umur > 55 tahun
Apabila seseorang berusia 34 tahun, maka ia dikatakan MUDA, MUDA[34]=1
Apabila seseorang berusia 35 tahun, maka ia dikatakan TIDAK MUDA,
MUDA[35]=0
Apabila seseorang berusia 35 tahun, maka ia dikatakan PAROBAYA,
PAROBAYA[35]=1
Apabila seseorang berusia 35 tahun kurang 1 hari, maka ia dikatakan TIDAK
PAROBAYA, PAROBAYA[35-1]=0
Apabila seseorang berusia 55 tahun, maka ia dikatakan TIDAK TUA,
TUA[55]=0
Apabila seseorang berusia 55 tahun lebih ½ hari, maka ia dikatakan TUA,
TUA[55+0.5]=1
Tidak adil bukan ?
8](https://image.slidesharecdn.com/ai2011-5-logika-fuzzy1-230623123530-b4c6c712/85/Kecerdasan-Buatan-8-320.jpg)
![Himpunan Fuzzy
Digunakan untuk mengantisipasi dimana sesorang dapat masuk dalam 2
himpunan yang berbeda.
◦ Misal, MUDA dan PAROBAYA, atau PAROBAYA dan TUA.
Contoh (dari gambar):
◦ Seseorang yang berusia 40 tahun, masuk dalam himpunan MUDA dengan MUDA[40]
=0.25; Tapi juga masuk dalam himpunan PAROBAYA dengan PAROBAYA[40]=0.5
◦ Seseorang yang berusia 50 tahun, masuk dalam himpunan PAROBAYA dengan
PAROBAYA[50]=0.5; Tapi juga masuk dalam himpunan TUA dengan TUA[50]=0.25
Jangkauan nilai keanggotaan setiap item data dalam rentang 0 dan 1:
◦ Jika suatu item x mempunyai nilai keanggotaan fuzzy A[x]=0 maka item tersebut
tidak menjadi anggota himpunan A
◦ Jika suatu item x mempunyai nilai keanggotaan fuzzy A[x]=1 maka item tersebut
menjadi anggota penuh himpunan A
9](https://image.slidesharecdn.com/ai2011-5-logika-fuzzy1-230623123530-b4c6c712/85/Kecerdasan-Buatan-9-320.jpg)

![Himpunan Fuzzy – Cont’d
Himpunan fuzzy memiliki 2 atribut, yaitu :
◦ Linguistik, yaitu penamaan suatu group yang mewakili suatu kondisi, misalnya: MUDA,
PAROBAYA, TUA
◦ Numeris, yaitu ukuran dari suatu variabel seperti : 30,40, 55, 65, dst
Himpunan Semesta
◦ Adalah keseluruhan nilai yang boleh dioperasikan dalam suatu variabel fuzzy.
◦ Contoh:
◦ Semesta untuk variabel umur : [0, ∞]
◦ Semesta untuk variabel berat badan : [1, 150]
◦ Semesta untuk variabel suhu : [0,100].
Domain himpunan fuzzy adalah keseluruhan nilai yang diizinkan dalam Semesta dan
boleh dioperasikan dalam suatu himpunan fuzzy.
◦ Contoh:
◦ MUDA = [0 45], PAROBAYA = [35 55], TUA = [45 +∞]
◦ DINGIN = [0 20], SEJUK = [15 25], NORMAL = [20 30], HANGAT = [25 35], PANAS = [30 40]
11](https://image.slidesharecdn.com/ai2011-5-logika-fuzzy1-230623123530-b4c6c712/85/Kecerdasan-Buatan-11-320.jpg)
![Fungsi Keanggotaan
Fungsi Keanggotaan (Membership Function) adalah suatu kurva yang
menunjukkan pemetaan titik-titik input data (sumbu x) kepada nilai
keanggotaannya (sering juga disebut derajat keanggotaan) yang
mempunyai interval mulai 0 sampai 1.
Menggunakan pendekatan fungsi:
◦ Linear naik
◦ Linear turun
◦ Kurva segitiga
◦ Kurva trapesium
◦ Kurva Sigmoid
◦ Kurva Phi
◦ Kurva Beta
◦ Kurva Gauss
Fungsi Linear naik dan Linear turun
◦ Berupa suatu garis lurus.
◦ Untuk Linear naik: dimulai dari derajat 0 bergerak kekanan menuju ke nilai domain yang
mempunyai derajat keanggotaan lebih tinggi.
◦ Untuk Linear naik: dimulai dari derajat 1 pada sisi kiri bergerak kekanan menuju ke nilai
domain yang mempunyai derajat keanggotaan lebih rendah.
12
Linear naik
b
x
b
x
a
a
b
a
x
a
x
x
,
1
,
)
/(
)
(
,
0
]
[
](https://image.slidesharecdn.com/ai2011-5-logika-fuzzy1-230623123530-b4c6c712/85/Kecerdasan-Buatan-12-320.jpg)
![13
Linear turun
b
x
b
x
a
a
b
x
b
a
x
x
,
0
,
)
/(
)
(
,
1
]
[
Fungsi Kurva segitiga
Merupakan gabungan garis
linear naik dan turun
c
x
b
b
c
x
c
b
x
a
a
b
x
b
c
x
a
x
x
,
)
/(
)
(
,
)
/(
)
(
atau
,
0
]
[
Fungsi Kurva trapesium
Pada dasarnya adalah kurva segitiga,
hanya saja ada beberapa titik ditengah
yang mempunyai nilai keangotaan 1
d
x
c
,
)
/(
)
(
c
x
b
,
1
b
x
a
,
)
/(
)
(
atau
,
0
]
[
c
d
x
d
a
b
a
x
d
x
a
x
x
](https://image.slidesharecdn.com/ai2011-5-logika-fuzzy1-230623123530-b4c6c712/85/Kecerdasan-Buatan-13-320.jpg)
![14
c
x
,
1
c
x
b
,
))
/(
)
((
2
1
b
x
a
,
))
/(
)
((
2
,
0
]
[ 2
2
a
c
x
c
a
c
a
x
a
x
x
Fungsi Kurva sigmoid
Digunakan untuk merepresentasikan kenaikan dan penurunan secara tidak
linear
•Untuk kurva sigmoid pertumbuhan bergerak dari sisi kiri (nilai
keangotaan=0) ke sisi kanan (nilai keanggotaan=1)
•Untuk kurva sigmoid penyusutan bergerak dari sisi kiri (nilai keangotaan=1)
ke sisi kanan (nilai keanggotaan=0)
Kurva sigmoid pertumbuhan
c
x
,
0
c
x
b
,
))
/(
)
((
2
b
x
a
,
))
/(
)
((
2
1
,
1
]
[ 2
2
a
c
x
c
a
c
a
x
a
x
x
Kurva sigmoid penyusutan](https://image.slidesharecdn.com/ai2011-5-logika-fuzzy1-230623123530-b4c6c712/85/Kecerdasan-Buatan-14-320.jpg)

![Operasi Himpunan Fuzzy
Seperti pada himpunan konvensional, ada operasi himpunan juga pada
himpunan fuzzy
◦ Hasil operasi 2 himpunan disebut juga fire strenght atau –predikat.
Ada 3 operator:
◦ AND (interseksi/irisan), dan OR (union/gabungan), NOT (komplemen)
Operator AND
◦ Berhubungan dengan operasi irisan himpunan,
◦ Diperoleh dengan mengambil nilai keanggotaan terkecil antar elemen pada himpunan-
himpunan yang bersangkutan.
◦ Misal: operasi AND nilai keanggotaan himpunan fuzzy A dan B, AB = min(A[x], A[y])
Operator OR
◦ Berhubungan dengan operasi union/gabungan himpunan,
◦ Diperoleh dengan mengambil nilai keanggotaan terbesar antar elemen pada himpunan-
himpunan yang bersangkutan.
◦ Misal: operasi OR nilai keanggotaan himpunan fuzzy A dan B, AB = max(A[x], A[y])
Operator NOT
◦ Berhubungan operasi komplemen pada himpunan.
◦ Misl, operasi NOT pada nilai keanggotaan A[x] menjadi: A[x]c = 1 - A[x]
16](https://image.slidesharecdn.com/ai2011-5-logika-fuzzy1-230623123530-b4c6c712/85/Kecerdasan-Buatan-16-320.jpg)



![20
Ada 3 variabel yang digunakan: PERMINTAAN, PERSEDIAAN, dan
PRODUKSI
PERMINTAAN: 1000 – 5000, x = 4000
PERSEDIAAN: 100 - 600, y = 300
PRODUKSI: 2000 – 7000, z = ?
PERMINTAAN, terdiri dari 2 himpunan fuzzy: TURUN dan NAIK
5000
,
0
5000
1000
,
4000
5000
1000
,
1
]
[
x
x
x
x
x
pmtTURUN
5000
,
1
5000
1000
,
4000
1000
1000
,
0
]
[
x
x
x
x
x
pmtNAIK
Nilai keanggotaan untuk nilai
PERMINTAAN = 4000
pmtTURUN[4000] = (5000-4000)/4000 = 0.25
pmtNAIK[4000] = (4000-1000)/4000 = 0.75
x = 4000](https://image.slidesharecdn.com/ai2011-5-logika-fuzzy1-230623123530-b4c6c712/85/Kecerdasan-Buatan-20-320.jpg)
![21
PERSEDIAAN, terdiri dari 2 himpunan fuzzy: SEDIKIT dan BANYAK
600
,
0
600
100
,
500
600
100
,
1
]
[
y
y
y
y
y
psdSEDIKIT
600
,
1
600
100
,
500
100
100
,
0
]
[
y
y
y
y
y
psdBANYAK
y = 300
psdSEDIKIT[300] = (600-300)/500 = 0.6
psdBANYAK[300] = (300-100)/500 = 0.4](https://image.slidesharecdn.com/ai2011-5-logika-fuzzy1-230623123530-b4c6c712/85/Kecerdasan-Buatan-21-320.jpg)
![22
PRODUKSI, terdiri dari 2 himpunan fuzzy: BERKURANG dan
BERTAMBAH
7000
,
0
7000
2000
,
5000
7000
2000
,
1
]
[
z
z
z
z
z
NG
prdBERKURA
7000
,
1
7000
2000
,
5000
2000
2000
,
0
]
[
z
z
z
z
z
AH
psdBERTAMB
Nilai -predikat dan Z dari setiap aturan
Rule 1
-predikat1 = pmtTURUN psdBANYAK
= min(pmtTURUN[4000]
psdBANYAK[300])
= min(0.25; 0.4)
= 0.25
Dari himpunan produksi barang
BERKURANG,
(7000-z)/5000 = 0.25 z1 = 5750
pmtTURUN = 0.25
pmtNAIK = 0.75
pmtSEDIKIT = 0.6
pmtBANYAK = 0.4
Rule 2
-predikat2 = pmtTURUN psdSEDIKIT
= min(pmtTURUN[4000]
psdSEDIKIT[300])
= min(0.25; 0.6)
= 0.25
Dari himpunan produksi barang
BERKURANG,
(7000-z)/5000 = 0.25 z2 = 5750](https://image.slidesharecdn.com/ai2011-5-logika-fuzzy1-230623123530-b4c6c712/85/Kecerdasan-Buatan-22-320.jpg)
![23
Rule 3
-predikat3 = pmtNAIK psdBANYAK
= min(pmtNAIK[4000]
psdBANYAK[300])
= min(0.75; 0.4)
= 0.4
Dari himpunan produksi barang
BERTAMBAH,
(z-2000)/5000 = 0.4 z3 = 4000
Rule 4
-predikat4 = pmtNAIK psdBANYAK
= min(pmtNAIK[4000]
psdBANYAK[300])
= min(0.75; 0.6)
= 0.6
Dari himpunan produksi barang
BERTAMBAH,
(z-2000)/5000 = 0.6 z4 = 5000
Menghitung z akhir dengan merata-rata semua z berbobot:
4
3
2
1
4
4
3
3
2
2
1
1
*
*
*
*
pred
pred
pred
pred
z
pred
z
pred
z
pred
z
pred
z
4983
5
.
1
7457
6
.
0
4
.
0
25
.
0
25
.
0
500
*
6
.
0
4000
*
4
.
0
5750
*
25
.
0
5750
*
25
.
0
z
Jadi, jumlah makanan jenis ABC yang harus diproduksi sebanyak
4983 kemasan.
Nilai -predikat dan Z dari setiap aturan](https://image.slidesharecdn.com/ai2011-5-logika-fuzzy1-230623123530-b4c6c712/85/Kecerdasan-Buatan-23-320.jpg)




![28
Ada 3 variabel yang digunakan: PERMINTAAN, PERSEDIAAN, dan
PRODUKSI
PERMINTAAN: 1000 – 5000, x = 4000
PERSEDIAAN: 100 - 600, y = 300
PRODUKSI: 2000 – 7000, z = ?
PERMINTAAN, terdiri dari 2 himpunan fuzzy: TURUN dan NAIK
5000
,
0
5000
1000
,
4000
5000
1000
,
1
]
[
x
x
x
x
x
pmtTURUN
5000
,
1
5000
1000
,
4000
1000
1000
,
0
]
[
x
x
x
x
x
pmtNAIK
Nilai keanggotaan untuk nilai
PERMINTAAN = 4000
pmtTURUN[4000] = (5000-4000)/4000 = 0.25
pmtNAIK[4000] = (4000-1000)/4000 = 0.75
x = 4000](https://image.slidesharecdn.com/ai2011-5-logika-fuzzy1-230623123530-b4c6c712/85/Kecerdasan-Buatan-28-320.jpg)
![29
PERSEDIAAN, terdiri dari 2 himpunan fuzzy: SEDIKIT dan BANYAK
600
,
0
600
100
,
500
600
100
,
1
]
[
y
y
y
y
y
psdSEDIKIT
600
,
1
600
100
,
500
100
100
,
0
]
[
y
y
y
y
y
psdBANYAK
y = 300
psdSEDIKIT[300] = (600-300)/500 = 0.6
psdBANYAK[300] = (300-100)/500 = 0.4](https://image.slidesharecdn.com/ai2011-5-logika-fuzzy1-230623123530-b4c6c712/85/Kecerdasan-Buatan-29-320.jpg)
![30
PRODUKSI, tidak mempunyai himpunan fuzzy.
Nilai permintaan = 4000 Jumlah persediaan = 300
Nilai -predikat dan Z dari setiap aturan
Rule 1
-predikat1 = pmtTURUN psdBANYAK
= min(pmtTURUN[4000]
psdBANYAK[300])
= min(0.25; 0.4)
= 0.25
Dari bagian konsekuen Rule 1
z1 = permintaan – persediaan
= 4000 – 300 = 3700
Rule 2
-predikat2 = pmtTURUN psdSEDIKIT
= min(pmtTURUN[4000]
psdSEDIKIT[300])
= min(0.25; 0.6)
= 0.25
Dari bagian konsekuen Rule 2
z2 = permintaan
= 4000
Rule 3
-predikat3 = pmtNAIK psdBANYAK
= min(pmtNAIK[4000]
psdBANYAK[300])
= min(0.75; 0.4)
= 0.4
Dari bagian konsekuen Rule 3
z3 = permintaan
= 4000
Rule 4
-predikat4 = pmtNAIK psdBANYAK
= min(pmtNAIK[4000]
psdBANYAK[300])
= min(0.75; 0.6)
= 0.6
Dari bagian konsekuen Rule 2
z2 = 1.25*permintaan - persediaan
= 1.25 * 4000 – 300 = 4700
Menghitung z akhir dengan merata-rata semua z berbobot:
4
3
2
1
4
4
3
3
2
2
1
1
*
*
*
*
pred
pred
pred
pred
z
pred
z
pred
z
pred
z
pred
z
4230
5
.
1
6345
6
.
0
4
.
0
25
.
0
25
.
0
4700
*
6
.
0
4000
*
4
.
0
4000
*
25
.
0
3700
*
25
.
0
z
Jadi, jumlah makanan
jenis ABC yang harus
diproduksi sebanyak
4230 kemasan.](https://image.slidesharecdn.com/ai2011-5-logika-fuzzy1-230623123530-b4c6c712/85/Kecerdasan-Buatan-30-320.jpg)



![Metode Komposisi Aturan
MAX
◦ Solusi himpunan diperoleh dengan cara mengambil nilai maksimum
aturan, kemudian menggunakannya untuk memodifikasi daerah fuzzy,
kemudian menerapkannya ke output dengan operator OR. Dirumuskan:
◦ sf[xi] max(sf[xi], kf[xi])
◦ Dimana: sf[xi] adalah nilai keanggotaan solusi fuzzy sampai aturan ke-i
◦ kf[xi] adalah nilai keanggotaan konsekuen fuzzy sampai aturan ke-i
Additive (sum)
◦ Solusi fuzzy diperoleh dengan melakukan bounded-sum pada semua
output daerah fuzzy. Dirumuskan:
◦ sf[xi] min(1, sf[xi]+ kf[xi])
Probabilistik OR (probor)
◦ Solusi fuzzy diperoleh dengan cara melakukan product terhadap semua
output daerah fuzzy. Dirumuskan:
◦ sf[xi] (sf[xi] + kf[xi]) - (sf[xi] * kf[xi])
34](https://image.slidesharecdn.com/ai2011-5-logika-fuzzy1-230623123530-b4c6c712/85/Kecerdasan-Buatan-34-320.jpg)
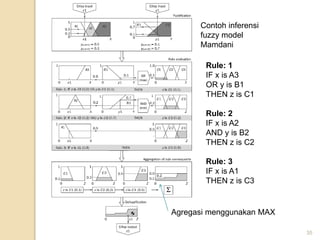


![38
Ada 3 variabel yang digunakan: PERMINTAAN, PERSEDIAAN, dan
PRODUKSI
PERMINTAAN: 1000 – 5000, x = 4000
PERSEDIAAN: 100 - 600, y = 300
PRODUKSI: 2000 – 7000, z = ?
PERMINTAAN, terdiri dari 2 himpunan fuzzy: TURUN dan NAIK
5000
,
0
5000
1000
,
4000
5000
1000
,
1
]
[
x
x
x
x
x
pmtTURUN
5000
,
1
5000
1000
,
4000
1000
1000
,
0
]
[
x
x
x
x
x
pmtNAIK
Nilai keanggotaan untuk nilai
PERMINTAAN = 4000
pmtTURUN[4000] = (5000-4000)/4000 = 0.25
pmtNAIK[4000] = (4000-1000)/4000 = 0.75
x = 4000
1
Pembentukan himpunan fuzzy](https://image.slidesharecdn.com/ai2011-5-logika-fuzzy1-230623123530-b4c6c712/85/Kecerdasan-Buatan-38-320.jpg)
![39
PERSEDIAAN, terdiri dari 2 himpunan fuzzy: SEDIKIT dan BANYAK
600
,
0
600
100
,
500
600
100
,
1
]
[
y
y
y
y
y
psdSEDIKIT
600
,
1
600
100
,
500
100
100
,
0
]
[
y
y
y
y
y
psdBANYAK
y = 300
psdSEDIKIT[300] = (600-300)/500 = 0.6
psdBANYAK[300] = (300-100)/500 = 0.4
1
Pembentukan himpunan fuzzy](https://image.slidesharecdn.com/ai2011-5-logika-fuzzy1-230623123530-b4c6c712/85/Kecerdasan-Buatan-39-320.jpg)
![40
Nilai -predikat dan Z dari setiap aturan
Rule 1
IF permintaan TURUN and persediaan BANYAK THEN produksi barang BERKURANG
-predikat1 = pmtTURUN psdBANYAK
= min(pmtTURUN[4000] psdBANYAK[300])
= min(0.25; 0.4)
= 0.25
pmtTURUN = 0.25
pmtNAIK = 0.75
pmtSEDIKIT = 0.6
pmtBANYAK = 0.4
Rule 2
IF permintaan TURUN and persediaan SEDIKIT THEN produksi barang BERKURANG
-predikat2 = pmtTURUN psdSEDIKIT
= min(pmtTURUN[4000] psdSEDIKIT[300])
= min(0.25; 0.6)
= 0.25
2](https://image.slidesharecdn.com/ai2011-5-logika-fuzzy1-230623123530-b4c6c712/85/Kecerdasan-Buatan-40-320.jpg)
![41
Rule 3
IF permintaan NAIK and persediaan BANYAK THEN produksi barang BERTAMBAH
-predikat3 = pmtNAIK psdBANYAK
= min(pmtNAIK[4000] psdBANYAK[300])
= min(0.75; 0.4)
= 0.4
Rule 4
IF permintaan NAIK and persediaan SEDIKIT THEN produksi barang BERTAMBAH
-predikat4 = pmtNAIK psdBANYAK
= min(pmtNAIK[4000] psdBANYAK[300])
= min(0.75; 0.6)
= 0.6
Nilai -predikat dan Z dari setiap aturan
pmtTURUN = 0.25
pmtNAIK = 0.75
pmtSEDIKIT = 0.6
pmtBANYAK = 0.4
2
Penerapan fungsi implikasi](https://image.slidesharecdn.com/ai2011-5-logika-fuzzy1-230623123530-b4c6c712/85/Kecerdasan-Buatan-41-320.jpg)
![42
Komposisi antar aturan
3
MAX
=
Daerah himpunan fuzzy terbagi 3: A1, A2, dan A3.
Mencari nilai a1, dan a2
(a – prod_minimal)/interval_prod = nilai_keanggotaan
(a1 – 2000)/5000 = 0.25 a1 = 3250
(a2 – 2000)/5000 = 0.6 a2 = 5000
Fungsi keanggotaan hasil komposisi:
5000
,
6
.
0
5000
3250
,
5000
/
)
2000
(
3250
,
25
.
0
]
[
z
z
z
z
z
](https://image.slidesharecdn.com/ai2011-5-logika-fuzzy1-230623123530-b4c6c712/85/Kecerdasan-Buatan-42-320.jpg)
![43
Defuzzifikasi / Menghitung z akhir
4
5000
,
6
.
0
5000
3250
,
5000
/
)
2000
(
3250
,
25
.
0
]
[
z
z
z
z
z
Menghitung z* menggunakan metode Centroid kontinyu
Moment
Daerah A2
Daerah A1 Daerah A3
Luas
1320312.5
M1
z
*
0.125
M1
dz
(0.25)z
M1
3250
0
2
3250
0
5
3187515.62
M2
0.2z
-
0.000067z
M2
dz
0.4z)
-
(0.0002z
M2
dz
z
5000
2000)
-
(z
M2
5000
3250
2
3
5000
3250
2
5000
3250
7200000
M3
z
*
0.3
M3
dz
(0.6)z
M3
7000
5000
2
7000
5000
812.5
A1
0
*
0.25
-
3250
*
0.25
A1
z
*
0.25
A1
dz
0.25
A1
3250
0
3250
0
743.75
A2
3250)
*
0.4
-
/10000
(3250
-
5000)
*
0.4
-
/10000
5000
(
A2
0.4z
-
/10000
z
A2
dz
0.4)
-
(z/5000
A2
zd
5000
2000)
-
(z
A2
2
2
5000
3250
2
5000
3250
5000
3250
200
1
A3
z
*
0.6
A3
dz
(0.6)
A3
7000
5000
7000
5000
](https://image.slidesharecdn.com/ai2011-5-logika-fuzzy1-230623123530-b4c6c712/85/Kecerdasan-Buatan-43-320.jpg)


