The document discusses Rudolf Kalman and his development of the Kalman filter, a mathematical method widely used in fields such as electrical engineering, mechanical engineering, and communications. It provides background on Kalman, an overview of the Kalman filter and how it works, and examples of its applications, notably in enabling the Apollo 11 moon landing through its use in the spacecraft's guidance system. The Kalman filter provides an efficient recursive solution to problems of discrete-time data filtering and estimation in dynamic systems with random noise.

1. Kalman Filters basics Tim Mazumdar BR Karthikeyan

2. The immortal one Hungarian-born U.S. scientist and professor Rudolf Emil Kalman (born 1930) is widely regarded as the creator of modern control theory and system theory. His research reshaped the field of control engineering. His most widely known accomplishment is his development of the Kalman filter, a mathematical method now widely used in of EE, ME and Communication. He was born in Budapest, Hungary, on May 19, 1930, the son of an electrical engineer. He immigrated to the United States in 1943, and studied EE at MIT. Kalman received his BSEE, MIT 1953 and his MSEE in 1954,. He got his PhD(1957) under John R. Ragazinni at Columbia. The original paper on Kalman filtering was entitled “A New Approach to Linear Filtering and Prediction Problems,” ASME—Transactions March 1960.

3. In Dedication to the man who taught K filtering Professor Uday B. Desai –respected academic, Professor at IIT, Bombay Father of Orthogonal Filters, the Desai-Weinert Smoother, the Robust Recursive Least Squares algorithm and about 100 other major innovations B Tech , IIT B- 1969-1974 PhD Johns Hopkins University – 1979. Currently Director IIT, Hyderabad

4. Objective Why Kalman filter? -background of the Kalman filter What is an innovations sequence and how it is generated the geometric idea behind innovations sequences Derivation of the Discrete Time Kalman Filter from first principles Prediction , Filtering, Smoothing and system identification How to build Practical Kalman filter Concepts – Kalman Gain, Process noise, Measurement noise, A-priori and a-posteriori measurement errors Example Kalman filters – some test cases Fast Kalman filters and Extended Kalman filters

5. Objectives Mathematical relationship between the K filter and RLS algorithms- Kalman filter as the underlying mathematical basis for RLS The Algebraic Riccati Equation and solving the ARE Apollo 11 Sextant

6. Definitions Linear Estimator Measurement noise – Noise added to a internal state variable to form a set of noisy observations. The idea is that the Kalman filter Estimation – Estimation of a state in the presence of process and measurement noise is the problem addressed by the K filter. It allows us to estimate the state of dynamic systems with certain types of random behavior using statistical moments e.g. mean. The K filter tracks the probability distribution of its estimation errors Kalman vs Weiner filters – Kalman filter is recursive in nature and updates the filter parameters upon receipt of every sample of obsrevation. Wiener requires the full set of observations to work. LQG – Linear quadratic Gaussian estimation problem. The estimator is linear function of observations. The estimate error is of quadratic form and the noise is Gaussian in amplitude

7. The Principle of Orthogonality Let x and z be two random variables and be an estimator for x. In estimation problems one tries to come up with a constant alpha that minimizes the expectation of the MSE. This gives rise to the principle The optimal estimate is a weighted function generally expressed as and estimate of x given that z is a set of observations. The other name is “Minimum variance unbiased estimator. The minimization of variance is due to the square nature of J and the unbiased estimate is due to the fact that J=E(…) =0 <..> stands for inner product in a Abstract vector space.

8. Elaboration of orthogonality Orthogonality is best explained geometrically in the context of estimation. Let z be a vector of observations and let the estimator be a linear function of z. That is in formal terms we are required to minimize In estimation the error is minimal is x- a1z is orthogonal to z. Perpendicular to the observations – as shown in the diagram below.

9. Controllability and Observability Kalman gave us some deep insights into the concepts of controllability and observability. A system is said to be controllable is there exists a set of control signal inputs uk defined over 0<=k<=N that can make the system transition from state x0 to state xN in N sampling instants, where N is a positive integer. For a state variable model this can be formally expressed as ollows. The defintion of observaility implies by using only the H matrix or its inverse it is possible to determine the system state at any time by using x = inv(H)*Y. This implies the observability matrix has a rank of N. this is formally expressed as

10. Kailath’s original 1970 definition of innovations process Given a stochastic process, its innovations process will be defined as a white Gaussian noise process obtained from the original process by a causally invertible transformation. What is a Causally invertible transformation- A casually invertible transformation is a mathematical operation that allows one to transform the white Gaussian noise process back to the original stochastic process. Smoother – A Smoother is a form of optimal filter which predicts the state of a system at t = kT with samples from before (like (k-1)T, (k-2)T … ) and after ( like (k+1)T, (k+2)T , …. Fixed interval smoother – a popular form of Kalman filter or smoother which uses all the observations of a fixed length interval to estimate the system state at all times during at interval. Mostly operate on a off-line basis. Fixed- point smoothers – Estimate the system state at (k-m)T using all observations up to current time.

11. Recursive nature of the Kalman Filter The Kalman filter is a set of mathematical equations that provides an efficient recursive computational solution to discrete time data filtering problems. The K filter removes extraneous &quot;noise&quot; from a given stream of data. Kalman’s greatest contribution was that he came up with two sets of algebraic equations that solve real-time problems. His solution to the discrete-time problem led him to tackle the continuous-time problem. He developed the continuous-time version of the K. filter with Richard Bucy (1960 – 1961) and published the all-important paper that describes a way to recursively find solutions to the discrete-data linear filtering problem.

12. What made the Kalman filter so celebrated in Media Kalman’s original work was funded by Air Force Office of Scientific Research (AFOSR) as it related to space vehicles. The AFOSR sponsored the research done at RIAS by Kalman and Bucy. Kalman and Bucy's work revolutionized the field of estimation and had an enormous impact on the design and development of precise navigation systems. The Kalman filter was a major breakthrough in guidance technology. In fact the original paper is the 25 th most quoted Paper in all of EE. It was the basis of the Apollo Guidance system and it enabled the first moon landing. It was the core of a memo written by Donald Fraser in 1965 for Apollo Guidance systems “ Recursive filtering applied to system identification” and used by James Potter . It is debatable whether the moon landings were possible without the Kalman Filter. Stanley F. Schmidt had a key role in the proselytizing NASA on the K filter. Smith convinced his colleagues to study and use the K filter for the Apollo missions. He also wrote the first code. The Kalman filter solved two problems that NASA wanted to solve . DATA FUSION PROBLEM – where RADAR data is combined With inertial navigation sensor data. DATA REJECTION PROBLEM – data outliers Need to be rejected for the spacecraft to continue in its proper trajectory.

13. STRUCTURE OF THE GOVERNING KALMAN FILTER EQUATIONS STATE EQUATION STATE NOISE MEASUREMENT EQUATION MEASUREMENT NOISE

14. KALMAN FILTER IN TERMS OF PROBABILITY, STATISTICS, AND RANDOM PROCESS UP ARROW: TIME INDEPENDENT; DOWN ARROW: TIME DEPENDENT; RIGHT ARROW: DIRECT PROBLEM; LEFT ARROW: INVERSE PROBLEM. STATISTICS PROBABILITY SEQUENTIAL STATISTICAL ANALYSIS OF RANDOM PROCESS IS THE KALMAN FILTER RANDOM PROCESS

15. THE WAY KALMAN FILTER WORKS THE KALMAN FILTER DOES MANY THINGS AND CAN BE INTERPRETED IN MANY WAYS AS SHOWN IN THE NEXT SET OF SLIDES STATE EQUATION (IMPROVED QUAL + QUAN) STATE NOISE (EFFECT IS SUPRESSED) MEASUREMENT EQUATION (IMPROVED QUAL + QUAN) MEASUREMENT NOISE

16. MANY THINGS WHICH KALMAN FILTER DOES-1 (FROM AIAA-2000-4319) FILTERS THE NOISES ESTIMATES THE STATES ESTIMATES PARAMETERS IDENTIFIES QUALITATIVELY THE STATE AND THE MEASUREMENT MODELS ESTIMATES QUANTITATIVELY THE PARAMETERS IN THE ABOVE MODELS FUSES/INTEGRATES THE DATA FROM DIFFERENT MEASUREMENT SOURCES – DATA FUSION FILTERS OUTLIERS IN MEASUREMENT ASSIMILATES THE DATA FROM DIFFERENT SOURCES AND IMPROVES BOTH THE STATE AND MEASUREMENT MODELS HISTORICALLY KALMAN FILTER HAS BEEN EVOLVED TO DO THE ABOVE TASKS WHICH ARE INCREASINGLY MORE INVOLVED

17. MANY THINGS WHICH KALMAN FILTER DOES-2 (FROM AIAA-2000-4319) UNOBSERVABLES FROM OBSERVABLES EXPANSION OF THE SCENARIO ESTIMATIMATION OF UNMODELLABLE INPUTS BY MODELLING AS NOISE PROBABILISTIC MIXING HANDLING DETERMINISTIC ERRORS BY NOISE ADDITION HANDLING NUMERICAL ERRORS AS NOISE ADDITION IT IS A STOCHASTIC CORRECTIVE PROCESS REVERSING AN IRREVERSIBLE PROCESS MANY MORE INTERPRETATIONS ARE POSSIBLE

18. DEFINITION OF KALMAN FILTER The Kalman filter assimilates the measurement information with uncertain system and measurement models based on probabilistic weighted linear addition of the predicted state and the measurement data to adapt both the state and measurement models in a statistically consistent way. Another interpretation is the Kalman filter (KF) is an expanding knowledge front by assimilating newer information in a meaningful way.

19. Mathematics of the Kalman filter- Bishop’s approach

20. Bishop and Welch - Kalman The state variable model for the Kalman filter. Insert equations 9 through 13 here : The first task during the measurement update is to compute the Kalman gain, The next step is to actually measure the process to obtain , and then to generate an a posteriori state estimate by incorporating the measurement as in (12). The final step is to obtain an a posteriori error covariance estimate via (1.13). The difference between the Kalman and Weiner filters is that the Kalman filter is recursive And at each time step the Kalman gain is computed.

21. Complete update of Kalman filter Each step require solving 5 equations. Nevertheless in modern day processors It is possible to solve the K filter equations either in SW as embedded code or in HW. There have been K filters designed for Systolic array based computation one of which we Will review in this session. Sorenson 1971- the quantity zk –Hxk is known in Kalman filtering as “residual”.

22. One way of looking at a single cycle of computation Time update projects the current estimate of state ahead in time. Measurement update updates the projected estimate by an additional observation at time k.

23. Some Process related definitions Stationary- If the mean and standard deviation are indepepent of the origin then a process is said to be stationary in the wide sense. Much of communication theory relies on the mathematics of stationary processes Ergodic – If the PD of its values at a single time instant over the ensemble of sample functions equals the PD over all time values of randomly chosen member functions. Ergodicity and Stationarity are independent characteristics.

24. 3 types of Estimation Filtering- filtering uses previous as well as the current observation to estimate the state if a linear system Prediction- Prediction uses previous observations to predict the state of a linear system in future time instants Smoothing- Use observations from the future and previous observations to estimate the state of a dynamical system Unbiased estimator – The K filter computes the conditional mean and variance of the PDF of the state vector of a linear system. The process noise and measurement noise must be white Gaussian. In case of a continuous time Kalman filter the conditional mean is propagated as a linear Differential equation or a L. Difference equation. The variance is propagated by a second order differential equation or its difference equation equivalent.

25. Setting up the plant >> A = [ 1.1269 -0.4940 0.1129; 1 0 0 ; 0 1 0 ]; >> A A = 1.1269 -0.4940 0.1129 1.0000 0 0 0 1.0000 0 >> B = [ -0.3832; 0.5919; 0.5191]; >> C = [ 1 0 0]; >> Bp = B'; >> Bp Bp = -0.3832 0.5919 0.5191 >> Plant = ss(A,[B B],C,0,-1,'inputname',{'u' 'w'}, 'outputname‘’,'y1‘,’y2’}); Q = 1; R = 1; [kalmf,L,P,K] = kalman(Plant,Q,R); >> K K = 0.3798 0.0817 -0.2570 K is really the Kalman gain

26. One we find the Kalman gain The inputs are process noise and output observations the outputs are state estimates x(n) and the estimate of the next observation. kalmf u yv ye Xhat(n) Compute the first output of the kalmf function kalmf = kalmf(1,:); Kalmf

27. Kalman filter outputs a = x1_e x2_e x3_e x1_e 0.7683 -0.494 0.1129 x2_e 0.6202 0 0 x3_e -0.081732 1 0 b = u y x1_e -0.3832 0.3586 x2_e 0.5919 0.3798 x3_e 0.5191 0.08173 c = x1_e x2_e x3_e y_e 0.6202 0 0 d = u y y_e 0 0.3798

28. Beginnings- Discrete time State variable model

29. Discrete Kalman filter Time update equations

30. Discrete Kalman filter Time update equations

31. When does Kalman gain converge quickly? The Kalman gain converges quickly when both the process noise covariance and error noise covariance are constant. (Q and R are Constant) One approach is to run the n filter off-line to estimate the degree of perturbation due to Q and R and arrive at an estimate of the Kalman gain . This is known as Grewal’s method(1993) When does the word recursive imply? Recursive implies does not imply all previous observations are stored and required to be processed every time a new data sample is received. This non requirement of storage Implies that the K filter requires computation than a Weiner filter

32. What are the 3 underlying assumptions of the K filter The Kalman filter is essentially an optimal data processing algorithm . It combines all available measurement data , prior knowledge of the system and measurement sensors to produce an estimate of the system state in such a way that error is minimized statistically as the iterations progress. the assumption of linearity- Linear system analysis is standard and well understood and can be extended to non-linear system through linearization techniques. The assumption of whiteness of measurement and process noise – Whiteness implies the noise samples are not correlated in time. Simply if you know the noise value now it will not do you any good at another point in time. In real life white noise will have infinite energy as its PSD is flat and so it cannot exists. White noise can be approximated by real wideband noise and without white noise the mathematics of the Kalman filter is not tractable.

33. Whiteness

34. Continued 3. the assumption of Gaussian nature of noise - When a number of non-Gaussian RVs are added the result tends to Gaussian in the limit when the number of RVs tends to infinity. This is known as the strong form of the Central Limit theorem. While “whiteness” of measurement noise and process noise has to do with the PSD of noise , Gaussian nature implies the PDF of noise assumes a bell shaped curve for the range of amplitudes. Gaussian nature is independent of whiteness in fact it imposes and additional constraint on the noise. . Gaussian nature makes the mathematics more tractable as Gaussian PDF implies the first and second order conditional densities completely determine the observation and process noise.

35. What is the Riccati equation The ARE or algebraic Riccati equation is due to Jacopo Riccati in its continuous form. The Riccati equation occurs in Linear Quadratic Gaussian estimation theory. This is the original context under which the Riccati equation arises in control theory. There are two forms of the ARE – one for continuous time systems and Another for discrete time systems. We demonstrate both here so that the student has some understanding Of the near central importance of the ARE in both communication and Control.

36. The Discrete Algebraic Riccati equation The DARE is more applicable for discrete time control systems. The Riccati equations perform 3 things Allow prediction of the statistical performance of the estimator before the estimator is actually deployed ( a-priori). Allow computation of the optimal gain – or Kalman gain. for the simplest cases the Riccati equations can be solved analytically but usually there are robust numerical techniques to solve the Riccati equations - Laub’s method

37. Development of the Kalman Filter equations this development follows Monson Hayes it’s a lot less complicated. Next we need to define the Q and R matrices which are co variances of the process Noise and the measurement noise.

38. Expressions for Process noise and Measurement noise Process noise is the noise term added to the state estimation equation and Measurement noise is the noise term added to the output equation. Where the Hermitian conjugate of the noise vector really boils down to a simple Transpose. One objective is to derive the optimum Kalman Gain that minimizes MSE estimation error . We define the best possible Linear estimate based on observation y(i), given that the Observations are from 1,2,3,…n-1. We define the 2 error seqeunces.

39. The all important P matrix or error covariance matrix For each n , xhat(n-1|n-1) and P(n-1|n-1) are available. When a new observation y(n) occurs the new estimate for the state vector must be Computed and also the error covariance matrix P(n|n-1) is “propagated” To P(n|n). The evolution of the state vector follows the state variable model

40. Equations related a-priori and a-posteriori error

41. Step 2 : Incorporation of new measurement

42. Expression for updated estimate The next big conceptual jump the uncorrelated nature of the process noise And the measurement noise. E(v(n)w(n))= 0 ;E(v(n)x(n))= AE(v(n)E(x(n))+E(v(n)w(n))=0 This implies v(n) and x(n) are uncorrelated.

43. Error covariance matrix propagation Now we take the derivative of the error covariance matrix wrt. Kalman Gain

44. Final Expression for optimal gain

45. Closure: Plugging the optimal gain into error covariance For the final expression we plug the optimal Kalman gain value Into the error propagation covariance equation

46. Time and measurement updates for the continuous time Kalman filter The continuous time model of a linear stochastic system can be expressed as Follows.

47. Matlab Examples

48. This example directly applies K equations %Define the length of the simulation. nlen=20; %Define the system. Change these % to change the system. a=1; h=3; %Define the noise covariances. Q=0.01; R=2; % Preallocate memory for all arrays x=zeros(1,nlen); z=zeros(1,nlen); xapriori=zeros(1,nlen); xaposteriori=zeros(1,nlen); residual=zeros(1,nlen); papriori=ones(1,nlen); paposteriori=ones(1,nlen); k=zeros(1,nlen); % Calculate the process and measurement noise. w1=randn(1,nlen);v1=randn(1,nlen); w=w1*sqrt(Q); v=v1*sqrt(R); %Initial condition on the state, x. x_0=1.0; %Initial guesses for state and a posteriori covariance. xaposteriori_0=1.5; paposteriori_0=1; %Calculate the state and the output x(1)=a*x_0+w(1); z(1)=h*x(1)+v(1); %Predictor equations xapriori(1)=a*xaposteriori_0; residual(1)=z(1)-h*xapriori(1); papriori(1)=a*a*paposteriori_0+Q; %Corrector equations k(1)=h*papriori(1)/(h*h*papriori(1)+R); paposteriori(1)=papriori(1)*(1-h*k(1)); xaposteriori(1)=xapriori(1)+k(1)*residual(1);

49. This example directly applies K equations %Calculate the rest of the values. for j=2:nlen, %Calculate the state and the output x(j)=a*x(j-1)+w(j); z(j)=h*x(j)+v(j); %Predictor equations xapriori(j)=a*xaposteriori(j-1); residual(j)=z(j)-h*xapriori(j); papriori(j)=a*a*paposteriori(j-1)+Q; %Corrector equations k(j)=h*papriori(j)/(h*h*papriori(j)+R); paposteriori(j)=papriori(j)*(1-h*k(j)); xaposteriori(j)=xapriori(j)+k(j)*residual(j); end j=1:nlen; subplot(221); %Plot states and state estimates h1=stem(j+0.25,xapriori,'b'); hold on h2=stem(j+0.5,xaposteriori,'g'); h3=stem(j,x,'r'); hold off %Make nice formatting. legend([h1(1) h2(1) h3(1)],'a priori','a posteriori','exact'); title('State with a priori and a posteriori elements'); ylabel('State, x'); xlim=[0 length(j)+1]; set(gca,'XLim',xlim); subplot(223); %Plot errors h1=stem(j,x-xapriori,'b'); hold on h2=stem(j,x-xaposteriori,'g'); hold off legend([h1(1) h2(1)],'a priori','a posteriori'); title('Actual a priori and a posteriori error'); ylabel('Errors'); set(gca,'XLim',xlim); %Set limits the same as first graph

50. This example directly applies K equations %Plot errors subplot(223); h1=stem(j,x-xapriori,'b'); hold on h2=stem(j,x-xaposteriori,'g'); hold off legend([h1(1) h2(1)],'a priori','a posteriori'); title('Actual a priori and a posteriori error'); ylabel('Errors'); set(gca,'XLim',xlim); %Set limits the same as first graph %Plot kalman gain, k subplot(224); h1=stem(j,k,'b'); legend([h1(1)],'kalman gain'); title('Kalman gain'); ylabel('Kalman gain, k'); set(gca,'XLim',xlim); %Set limits the same as first graph

51. Curves for 1-D Kalman Filter

52. Another simple K filter for position

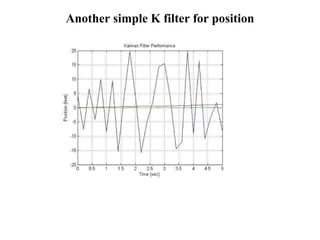
53. Kalman demo 1 duration=5; dt=0.2; [pos,posmeas,poshat]= kalman_demo1(duration,dt); Kalman_demo1 function is available from the instructor

54. A 4x4 Kalman filter example This example includes a 4x4 estimator for a movement of a point in 2 –dimensional Plane starting from (10,10) . Consider a particle moving in the plane at constant velocity subject to random perturbations in its trajectory. The new position (x1, x2) is the old position plus the velocity (dx1, dx2) plus noise w. [ x1(t) ] = [1 0 1 0] [ x1(t-1) ] + [ wx1 ] [ x2(t) ] [0 1 0 1] [ x2(t-1) ] +[ wx2 ] [ dx1(t) ] [0 0 1 0] [ dx1(t-1) ] +[ wdx1 ] [ dx2(t) ] [0 0 0 1] [ dx2(t-1) ]+ [ wdx2 ] We assume we only observe the position of the particle. [ y1(t) ] = [1 0 0 0] [ x1(t) ] + [ vx1 ] [ y2(t) ] [0 1 0 0] [ x2(t) ]+ [ vx2 ] [ dx1(t) ] [ dx2(t) ] Plant = ss(A,[B B],C,0,-1,'inputname',{'u' 'w'}, 'outputname‘’,'y1‘,’y2’}); [x,y] = sample_lds(F, H, Q, R, initx, T); [xfilt, Vfilt, VVfilt, loglik] = kalman_filter(y, F, H, Q, R, initx, initV);

55. >> F = [1 0 1 0; 0 1 0 1; 0 0 1 0; 0 0 0 1]; H = [1 0 0 0; 0 1 0 0]; Q = 0.1*eye(ss); R = 1*eye(os); >> F F =1 0 1 0 0 1 0 1 0 0 1 0 0 0 0 1

56. Kalman Filter “Covariance” Demo2 Another example of a Kalman filter with 3 axis position estimation. It also shows how the variance of the estimation error propagates between time steps and decreases as each measurement is processed. F = H = 0 1 0 1 0 0 0 0 1 0 0 0

57. “ Simon” the 3 rd Kalman example Position estimation of a vehicle is performed. The state consists of vehicle position and Velocity. Input u is “acceleration” and output “y” is the measured position Velocity at one time step from current = Current velocity + command acceleration* Kalman filter timing interval. .

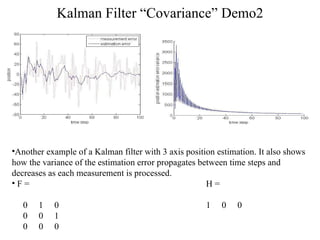
58. Building the F, H, G matrices T =.0.1sec; F= H = [ 1 0]; A = [ 1 0.1; 0 1]; B = [ 0.005; 0.1]; C = [ 1 0]; Xinit = [0;0];x = Xinit; xhat= Xinit; % Initital state estimate R = measnoise^2; % R matrix Sw = accelnoise^2*[ 1 0 ; 0 1]; % Q matrix P = Sw; % Defintion Position vector and Poistion estimated vectors pos = []; poshat = []; posmeas= []; vel = []; velhat = []; duration = 10;

59. Kalman Position Tracker for t = 0:dt:duration u = 1; % Simulate the Linear system Processnoise = accelnoise*[(dt^2/2)*randn; dt*randn]; x = A*x + B*u + Processnoise; % Simulate the obserbvation equation y = C*x + measnoise; % Update the state Estimate xhat = A*xhat +B*u; % Form the Innovation Vector Inno_vec = y - C*xhat; % Write the equation for Compuation of th Covariance of Innovations % Process S = C*P*C' + Sz; % Use the computed Covariance of Innovation to comnpute the Kalaman Gain% Gain K = A*P*C'*inv(S); % Update the State Estimate xhat = xhat + K*Inno_vec; % Compute the covariance of the EStimation Error P = A*P*A' -A*P*C'*inv(S)*C*P*A' + Sw; pos = [pos; x(1)]; posmeas = [posmeas; y]; poshat = [poshat; xhat(1)]; vel = [vel; x(2)]; velhat = [velhat; xhat(2)]; End close all; t = [0:dt:duration]; figure(1); Sw = 0.5*accelnoise^2*[ 1 0 ; 0 1]; % Q matrix P = Sw; plot(t,pos','b', t,posmeas','g',t,poshat','r');

60. Tracking error at two values of process noise This example is run for two different values of Process noise . The difference between The two estimates is telling. The second estimate of the position is much closer to the noisy measurement.

61. What are the key issues in implementation Verhaegen and Van Dooren proved in a legendary paper that the effectiveness of the K filter is dependent on the numerical accuracy with which the error covariance Matrix Or the P(n|n-1) matrix is represented. Loss of symmetry of the error Covariance matrix leads to seriosu issues with the implementation of the K. Filter. Numerical stability is exacerbated by due to the fact that the Riccatti Equation solution can get into trouble due to roundoff errors and the eignevalues Of the error covariance matrix can lead to a blowout of its condition number that is The ratio of the largest and smallest eignevalues. There many approaches to making the K filter more stable. No suprisingly one Approach – the Potter-Stern approach where P is not propagated but its Cholesky Transpose. P = CC’ Where C is propagated. Other approaches that have been tried is the QR decomposition and Bierman and Kailaths approaches. The most well known approach is called Square – root filters Which are reformulated K filters with better numerical stability

62. Equations to explain stability

63. A second way to write the propagated K filter error The Error covariance matrix can be distorted in two ways. Both of these ways are documented well by Sorenson (1971) and Verhaegen(1999). One is when Pk looses its symmetry its better to propagate a symmetric version of Pk. Pk Can loose its symmetry due to numerical errors as the Kalman filter processes. The Second type of numerical problem is when the error covariance matrix becomes too small thereby reducing the Kalman gain. Reduced Kalman gain implies newer Samples are given too little weight. This happens when the plant noise is very low.

64. Comparison of continuous time and discrete time Kalman filter equations

65. How do we relate the A.. F matrices? The best way is to use first order approximations to arrive at the difference from the Differential equations. The steps are not shown here but the final expressions are ,

66. Computational complexity of the Kalman filter It depends on the number of states in the state vector and the number of observations whichever is bigger. If the number of states is n and the number of observations is m the computational complexity can be very simply expressed as O(max(n^3,m^3)). This cubic relationship shows that the Kalman filter is really pretty computationally Complex- esp. compared to LMS or Fast LMS or even RLS.

67. Exactly what was Kalman’s contribution The two most significant contributions that the Kalman filter makes are as follows: The Kalman filter equations are very suitable for implementation by a digital computer. This is what led to its adoption as a core engine in the Apollo program. The user of a Kalman filter today just needs to know basic matrix operations without having any understanding of the underlying theory. Its is very easy to modify the Kalman filter Equations so that matrix inversion is avoided. It is especially so for (I-KC)^-1 In contrast the Weiner filter requires inversion of matrix and spectral factorization. The recursive nature of the Kalman filter and the fact that the update requires only one additional sample also helped in its adoption Kalman’s work triggered a whole flurry of theoretical work to design different types of Kalman filters suited for non-linear ( EKF or extended Kalman filtering) and even non-Gaussian noise situations. Kalman recognized the theoretical importance Of his work and capitalized on it. It was his state variable framework which gave rise To the additional theoretical work done on the Kalman filter

68. DKF and EKF DKF- Discrete Kalman Filter , this is the form in which Kalman invented the filter. Primarily applicable to linear state models it has been proven in practice for the last 50 years. DKF is a robust state estimator with separate models for process and measurement noise. It has been 3 assumptions of Maybeck, whiteness of process & measurement noise, Gaussianess or process noise and measurement noise and linear state equation. DKF is applicable to practically all forms of linear signal processing. EKF or Extended Kalman filter which is suited for non-linear state models. EKF has many flavors- in fact each author has come up with her/his interpretation of EKF EKF performance is mixed. It does not work very well if the process and measurement Noise differs from Gaussian.

69. 3 dimensional position tracking -an example

70. Full Form of A Matrix

71. How the matrix elements are derived

72. How the matrix elements are derived- Y axis This gives the second row of the A Matrix

73. Row 4 of the A matrix

74. Kalman filter for a second order system

75. Restructuring the DKF equations for HW implementation Reduces number of matrix multiplications by a quarter

76. THANKS

77. On Linear prediction for communications Mazumdar and Kadambi