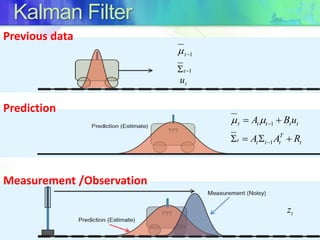
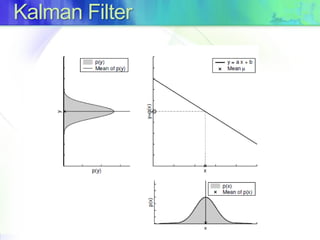
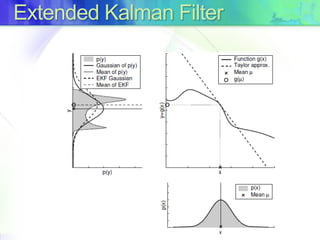
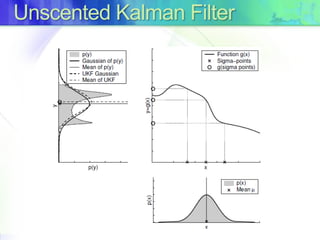
The document discusses Kalman filters and their applications in tracking and data prediction. It provides an overview of the basic Kalman filter, which works optimally for linear models. It then describes the extended Kalman filter (EKF) which uses Taylor series linearization to apply the Kalman filter to nonlinear systems. Finally, it introduces the unscented Kalman filter (UKF) which uses the unscented transform for better linearization compared to the EKF when nonlinearities are large.

1. Prepared by
Mohamed Attia Aref
mattia@eng.suez.edu.eg
May 2015

2. Objectives
Objectives
Applications
Basic Idea
Kalman
Algorithm
Extension
to
nonlinear
Extended
Kalman
Filter (EKF)
Unscented
Kalman
Filter
(UKF)

3. Kalman Filter Applications
•The Kalman filter has been used as an optimal solution to
many tracking and data prediction applications.

4. Kalman Filter (KF)
•Prof. Rudolf Kalman
(Born 1930 in Hungary)
•Developed filter in 1960/61
•The purpose of a Kalman filter is to estimate the state of
a system by processing all available measurements,
regardless of their precision.
•It works optimally for linear models and Gaussian
distributions.

5. Kalman Filter
The Kalman filter algorithm involves two stages:
1. Prediction
2. Measurement
tttttt uBxAx  1
tttt xCz 

6. Kalman Filter
t
The state transition matrix which applies the effect of each system
state parameter at time t-1 on the system state at time t without
controls or noise.
tA
The control input matrix which applies the effect of each control
input parameter in the vector ut on the state vector xt .tB
The transformation matrix that maps the state vector xt
parameters into the measurement domain zt .tC
t
Random variables representing the process and measurement
noise that are assumed to be independent and normally
distributed with covariance Rt and Qt respectively.
The state vector containing the terms of interest for the system
(e.g., position, velocity, heading) at time t
The vector containing any control inputs (steering angle, braking
force).
The vector of measurements.
tx
tu
tz

7. Kalman Filter

8. Kalman Filter
ttttt uBA  1
t
T
tttt RAA  1
1t
1t
tu
Prediction
Measurement /Observation
Previous data
tz

9. Kalman Filter
Measurement update/correction
)( tttttt CzK  
tttt CKI  )(
1
)( 
 t
T
ttt
T
ttt QCCCK Kalman gain
1
)0( 
 T
ttt
T
ttt CCCK
1111
)( 
 ttt
T
t
T
tt CCCC
tttttttttttt CCzCCzC  111
)( 

tttttt zCzC 11 
 
0tQAt :

10. Kalman Filter
Kalman filter algorithm

11. Kalman Filter
Most realistic problems involve nonlinear
functions

12. Kalman Filter

13. Kalman Filter

14. Kalman Filter
•The non-linear functions lead to non-Gaussian
distributions.
•Kalman filter is not applicable anymore!
Solution?
Local Linearization

15. Prediction:
Correction:
Extended Kalman Filter (EKF)
)(),(),(
)(
),(
),(),(
1111
11
1
1
11










ttttttt
tt
t
tt
tttt
xGugxug
x
x
ug
ugxug




)()()(
)(
)(
)()(
ttttt
tt
t
t
tt
xHhxh
x
x
h
hxh









Linearization using Taylor Series Expansion
Linear functions
(Jacobian matrices)

16. Extended Kalman Filter

17. Extended Kalman Filter
Extended Kalman filter algorithm

18. Extended Kalman Filter
• Not optimal!
• Can diverge if nonlinearities are large!
better way to do linearization?
Unscented Transform (UT)

19. Unscented Kalman Filter (UKF)

20. Unscented Kalman Filter

21. Unscented Kalman Filter

22. Unscented Kalman Filter

23. Unscented Kalman Filter
  ni
n
wwn
n
w
n
w
i
c
i
mi
i
cm
2,...,1for
)(2
1
)(
)1( 2000
















Sigma points Weights

24. Unscented Kalman Filter

25. Unscented Kalman Filter

26. Unscented Kalman Filter
Unscented Kalman filter algorithm

27. Unscented Kalman Filter

29. References
1. S. Thrun, W. Burgard,“Probabilistic Robotics”, Chapter 3.
2. Julier and Uhlmann,“A New Extension of the Kalman Filter
to Nonlinear Systems”, 1995.
3. Ramsey Faragher, “Understanding the Basis of the
Kalman Filter Via a Simple and Intuitive Derivation”, IEEE
SIGNAL PROCESSING MAGAZINE, Sept.2012.
4. Cyrill Stachniss, “Robot Mapping lectures”, Uni. Freiburg,
WS 2013/14 .