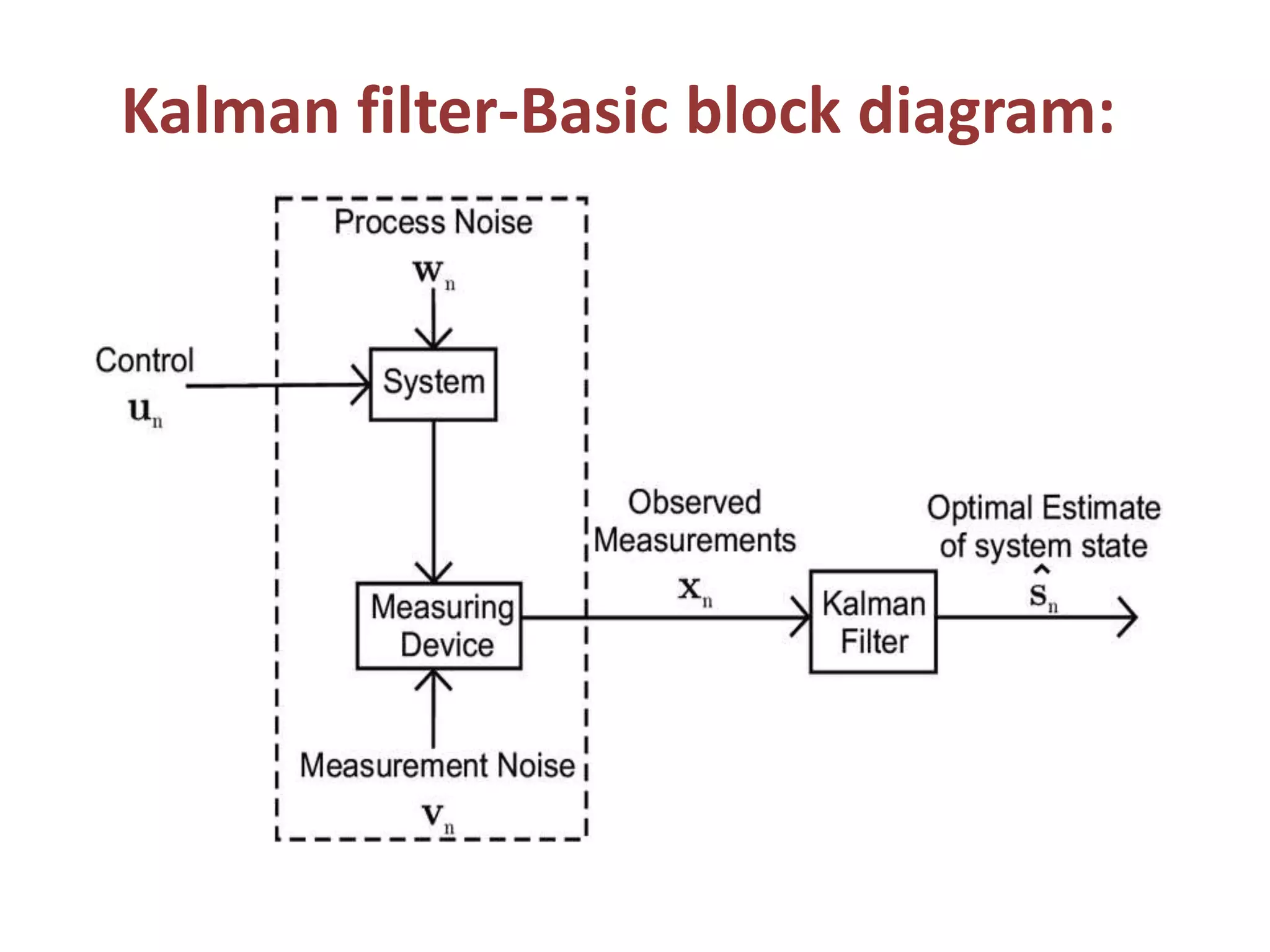
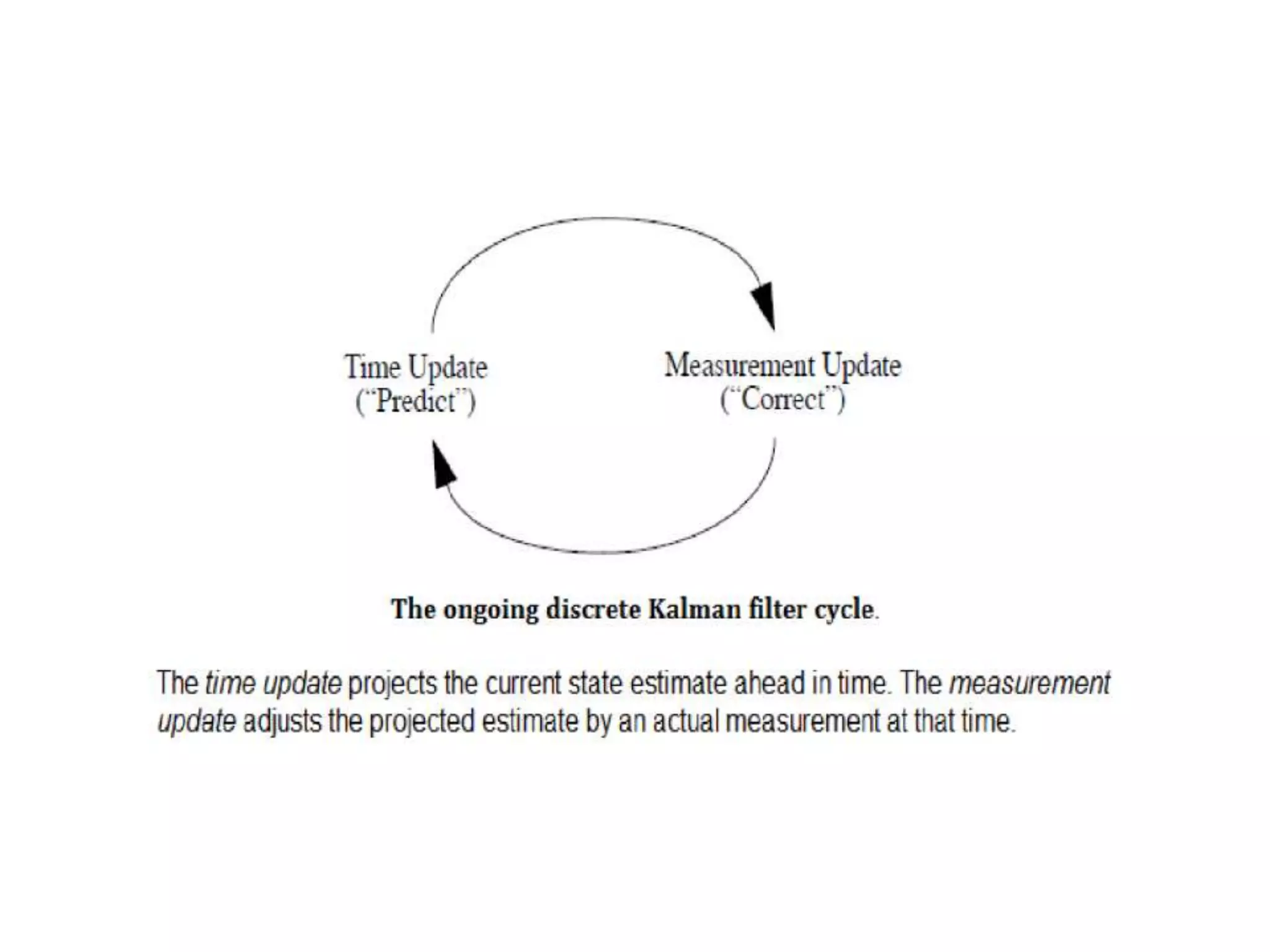
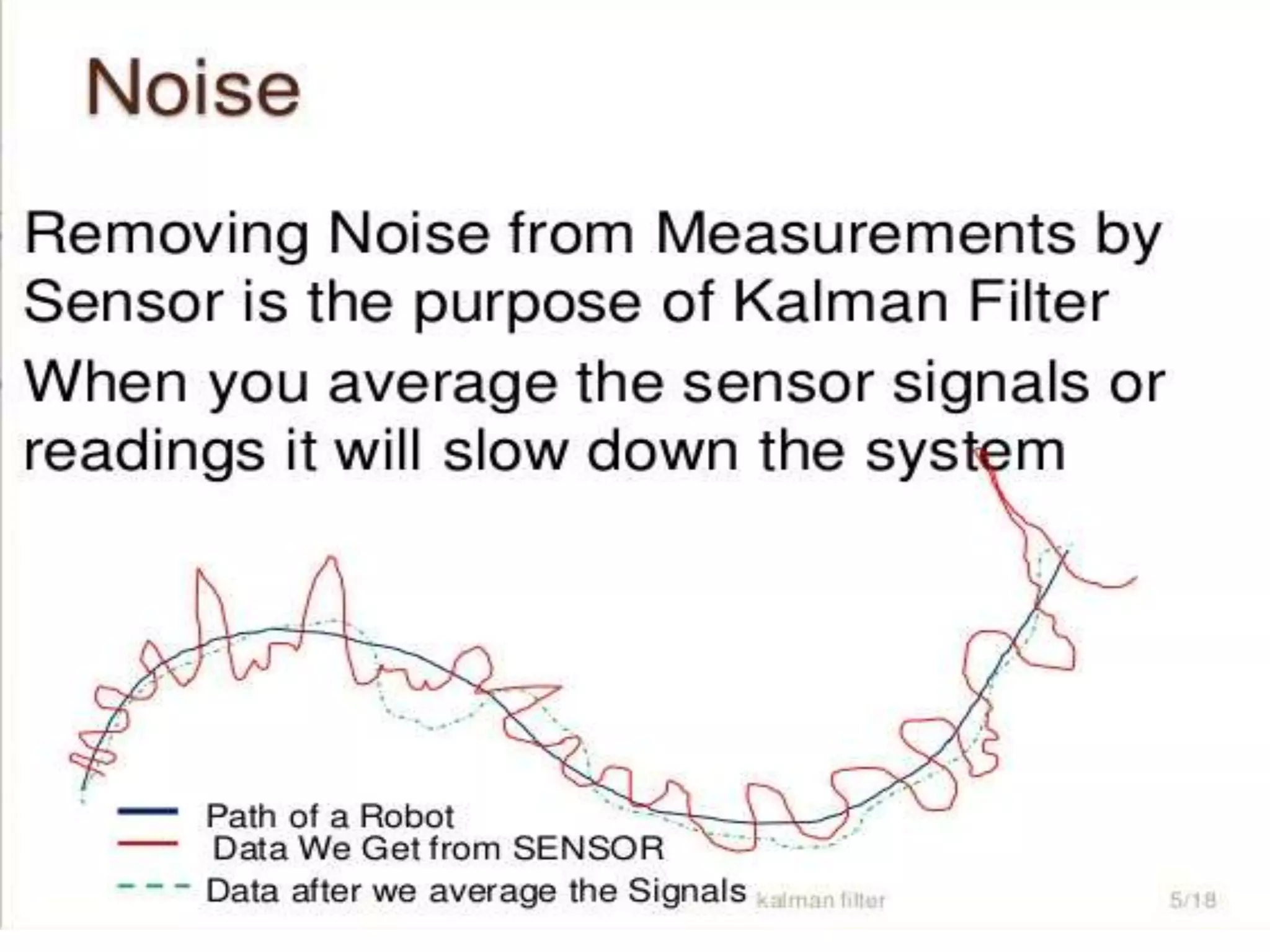
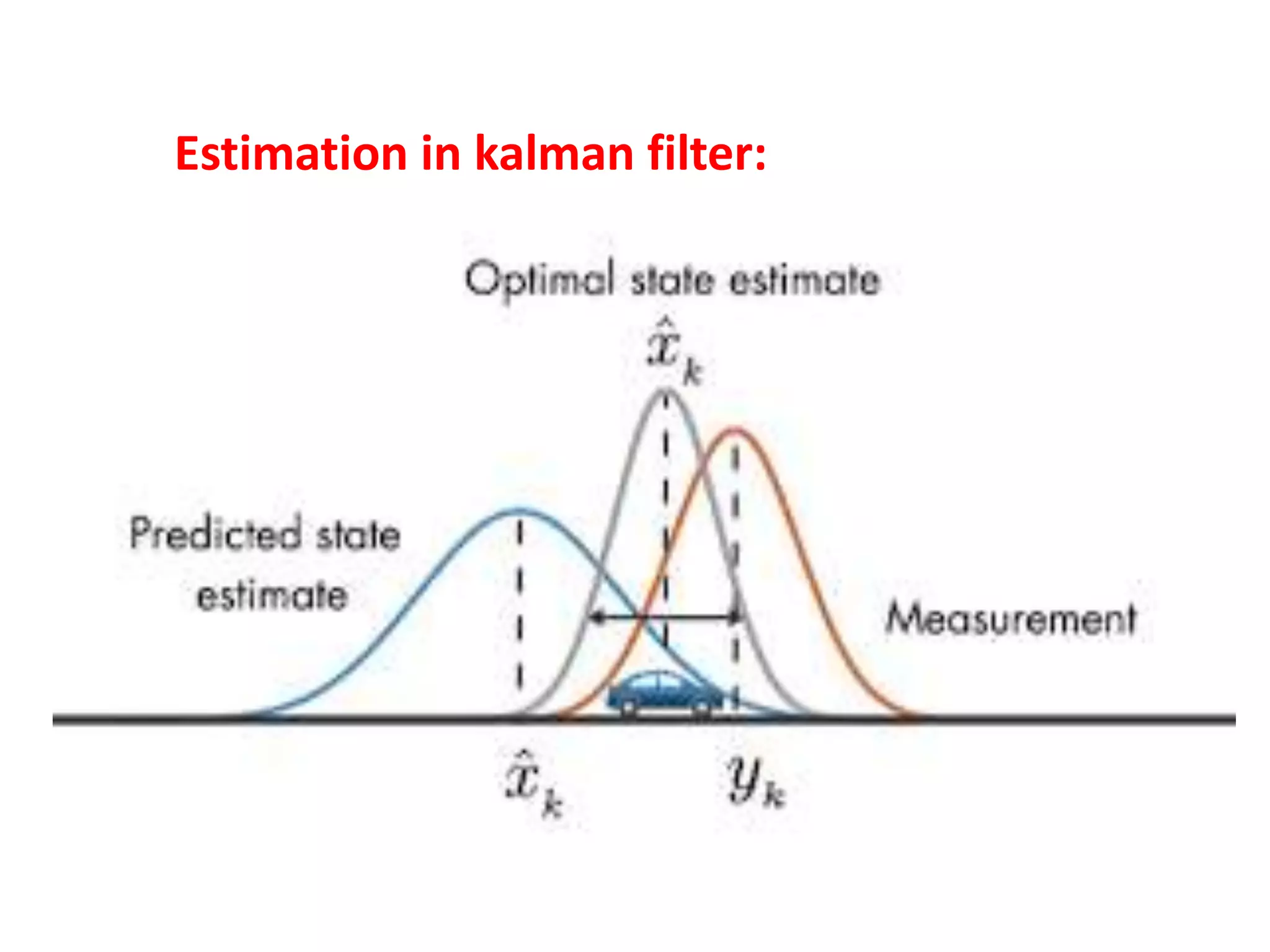
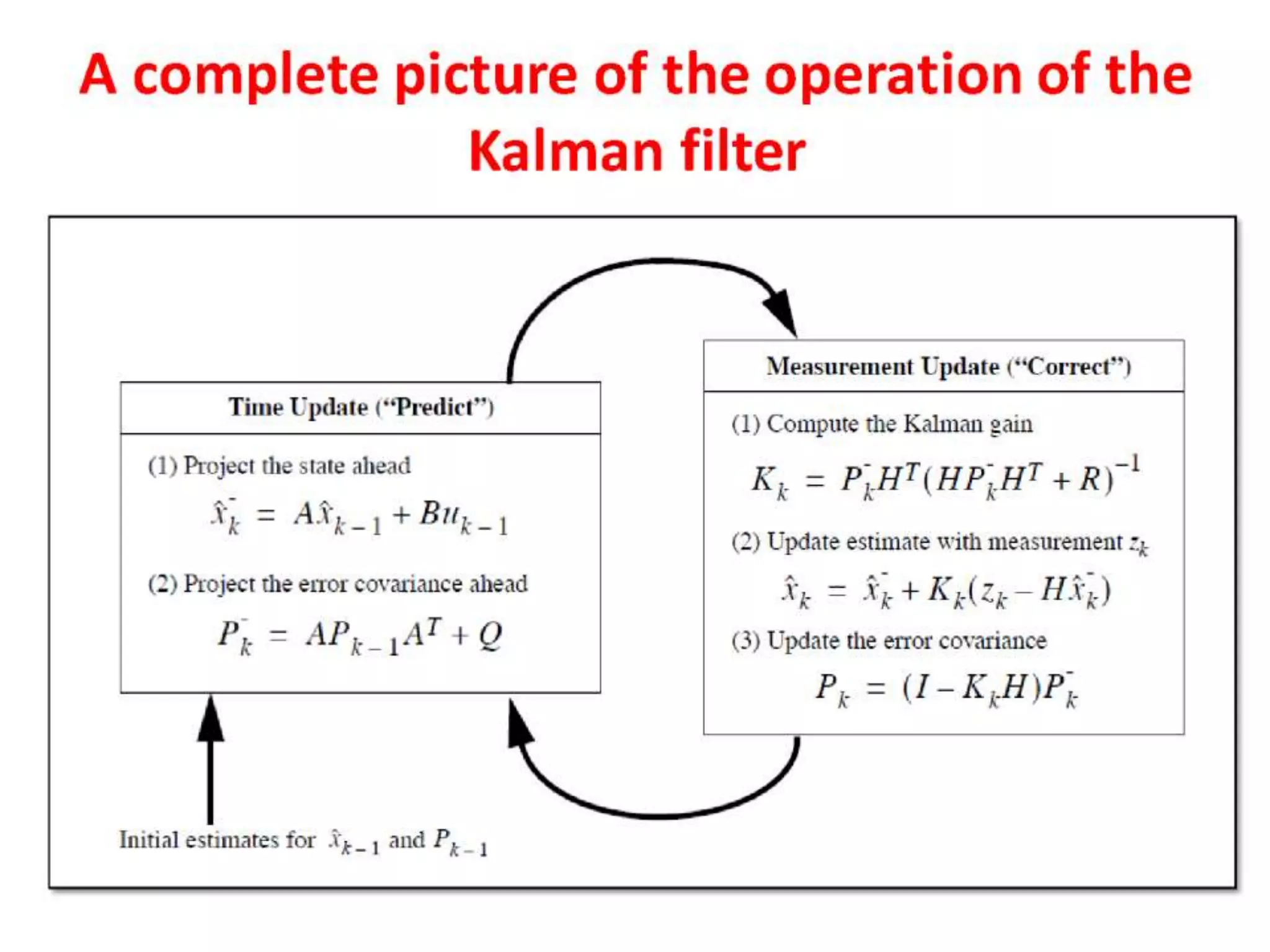
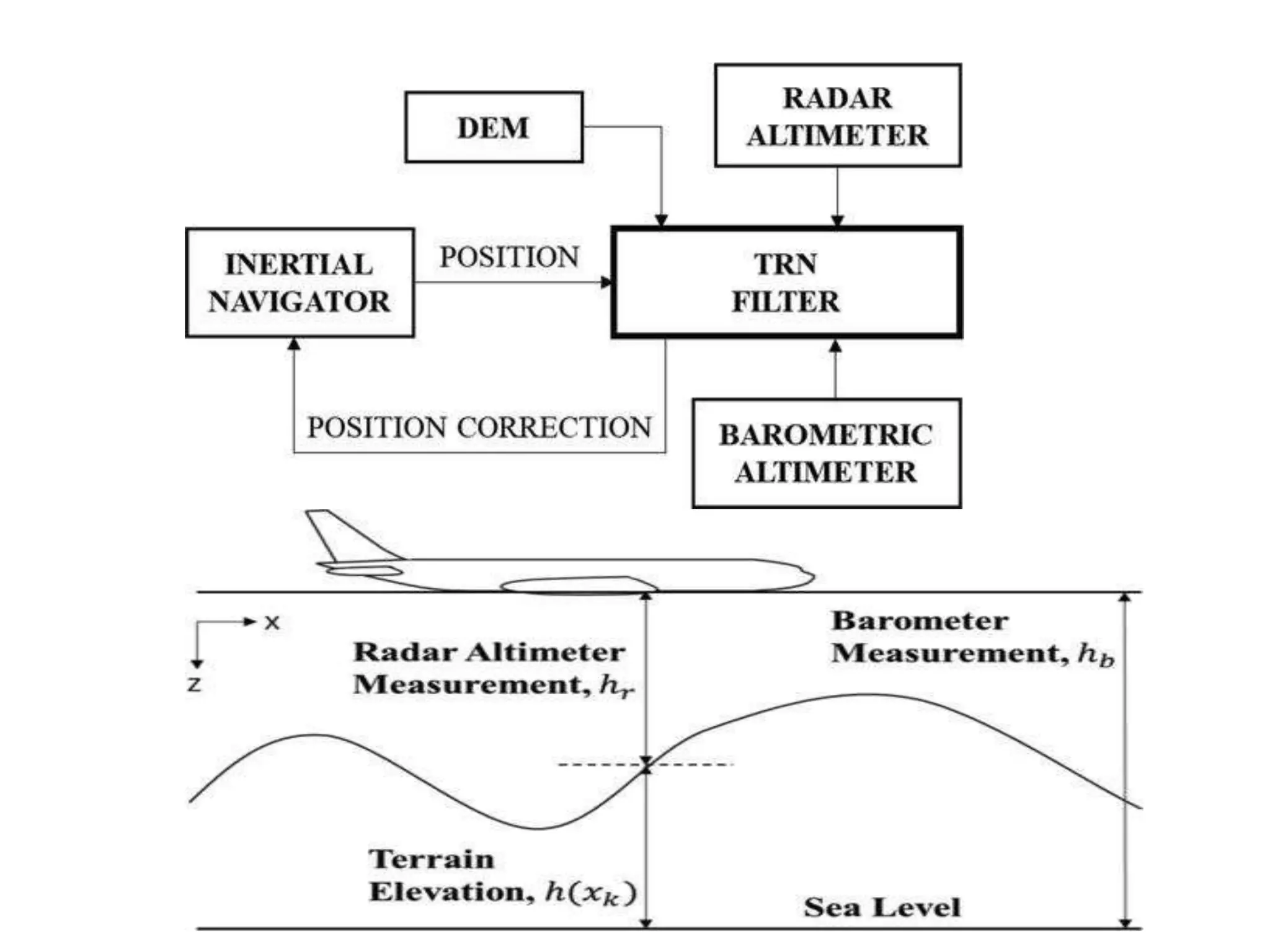
The document discusses the development and theory of Kalman filtering, an algorithm that provides more accurate estimates of unknown variables through a series of measurements over time despite statistical noise. It covers its background, including Rudolf Kalman's contributions and the mathematical models behind the filtering process. Additionally, it highlights several applications of Kalman filters, such as image processing, GPS tracking, and terrain-referenced navigation.

1. KALMAN FILTERING &
ITS APPLICATIONS
PREPARED BY:
Y.MADHAVASAI
17A51A04B8

2. Rudolf Kalman was born in Hungary on 19 May 1930.
He completed his Master's degree in Electrical
Engineering from Madras institute of technology in
1953-54 respectively.
 He left M.I.T. and continued his studies at Columbia
University where he received his ScD. in 1957 under
the direction of Professor J. R. Ragazzini.
Based on recursive Bayesian he developed a filter in
two years time period i.e., from 1960-61.
Rudolf e kalman

3.  In statistics and control theory, Kalman filtering,
also known as linear quadratic estimation (LQE),
 It is an algorithm that uses a series of
measurements observed over time,
containing statistical noise and other inaccuracies
 It produces estimates of unknown variables that
tend to be more accurate than those based on a
single measurement alone, by estimating a joint
probability distribution over the variables for each
timeframe.
 The filter is named after Rudolf E. Kálmán , one of
the primary developers of its theory.

4. Kalman filter-Basic block diagram:

5. • A kalman filter is a more sophisticated
smoothing algorithm that will actually change
in real time as the performance of various
sensors change and become more or less
reliable.
• What you want to do is filter out noise in our
measurements and in our sensors and kalman
filter is one way to do that reliability

6. Kalman filters are used to estimate states
based on linear dynamical systems in state
space format.
The process model defines the evolution of
the state from time k−1 to time k as:
xk=Fxk−1+Buk−1+wk−1
Where, F -state transition matrix
B -control-input matrix
Wk−1 - noise vector assumed to be
zero mean gaussin .

7. The process model is paired with the measurement
model that describes the relationship between the
state and the measurement at the current time step k
as:
zk=Hxk+νk
where zk is the measurement vector,
H is the measurement matrix, and
νk is the measurement noise vector that is
assumed to be zero
NOTE : sometimes the term “measurement” is
called “observation” in different literature

12. Estimation in kalman filter:

14. APPLICATIONS
Image processing
 Terrain-referenced navigation
Gps tracking devices
Computer vision

18.  TERRAIN-REFERENCED NAVIGATION
1)Terrain-referenced navigation (TRN), also known as
terrain-aided navigation (TAN)
2)it provides positioning data by comparing terrain
measurements with a digital elevation model (DEM)
stored on an on-board computer of an aircraft.
3)It also known as terrain-aided navigation (TAN),

20. Gps tracking devices