Ism et chapter_6

1
6. sec 2t tan 2t dt = sec 2t + c
2

7. (x2 + 4)2 dx = (x4 + 8x2 + 16)dx
x5 8
= + x3 + 16x + c
5 3
Chapter 6
8. x(x2 + 4)2 dx = (x5 + 8x3 + 16x)dx
x6
= + 2x4 + 8x2 + c
Integration 3
6
3 x
9. dx = tan−1 + c
Techniques 16 + x2
2
4
1
4

10. 2
dx = tan−1 x + c
4 + 4x 2
1
11. √ dx
3 − 2x − x2
6.1 Review of Formulas 1 x+1
= dx = arcsin +c
and Techniques 4 − (x + 1)2 2

1 ax x+1
1. eax dx = e + c, for a = 0. 12. √ dx
a 3 − 2x − x2
1 −2(x + 1)
=− dx
1 2 4 − (x + 1)2
2. cos(ax)dx = sin(ax) + c, for a = 0.
a 1
= − · 2[4 − (x + 1)2 ]1/2 + C
2
1 1 1
3. √ dx = dx = − 4 − (x + 1)2 + c
a2 − x2 x 2 a
1− a 4
x 1 13. dx
Let u = , du = dx. 5 + 2x + x2
a a 1 x+1
1 =4 dx = 2 tan−1 +c
= √ du = sin−1 (u) + c 4 + (x + 1)2 2
1 − u2
−1 x
= sin + c, a > 0. 4x + 4
a 14. dx
5 + 2x + x2
b 2(x + 1)
4. √ dx =2 dx = 2 ln | 4 + (x + 1)2 | + c
|x| x2 − a2 4 + (x + 1)2
b 1 4t
= dx 15. dt
x 2 a 5 + 2t + t2
|x| a −1
4t + 4 4
x 1 = dt − dt
Let u = , du = dx and |au| = |x| . 5 + 2t + t2 5 + 2t + t2
a a t+1
b = 2 ln 4 + (t + 1)
2
− 2tan−1 +c
= √ du 2
|au| u2 − 1
b 1 t+1 2 (t + 1)
= √ du 16. dt = dt
|a| |u| u2 − 1 t2 + 2t + 4 2
(t + 1) + 3
b 1
= sec−1 (u) + c 2
= ln (t + 1) + 3 + c
|a| 2
b x
= sec−1 + c, a > 0. 17.
1
e3−2x dx = − e3−2x + c
|a| a 2
1 3
5. sin(6t)dt = − cos(6t) + c 18. 3e−6x dx = − e−6x + c
6 6

360

6.1. REVIEW OF FORMULAS AND TECHNIQUES 361

2 −1/3 30. Let u = ex , du = ex dx
19. Let u = 1 + x2/3 , du = x dx
3 ex 1
4 3 √ dx = √ du
dx = 4 u−1 du 1 − e2x 1 − u2
x1/3 (1 + x2/3 ) 2
= sin−1 u + C = sin−1 ex + c
2/3
= 6 ln |u| + C = 6 ln |1 + x |+c
31. Let u = x2 , du = 2xdx
3 x 1 1
20. Let u = 1 + x3/4 , du = x−1/4 dx √ dx = √ du
4 1 − x4 2 1 − u2
2 2
dx = dx 1 1
x1/4 + x x1/4 (1 + x3/4 ) = sin−1 u + C = sin−1 x2 + c
4 8 2 2
=2 u−1 du = ln |u| + C
3 3 32. Let u = 1 − x4 , du = −4x3 dx
8 2x3 1
= ln |1 + x3/4 | + c √ dx = − u−1/2 du
3 1−x 4 2
√ 1 = −u1/2 + C = −(1 − x4 )1/2 + c
21. Let u = x, du = √ dx
√ 2 x
sin x 1+x
√ dx = 2 sin udu 33. dx
x 1 + x2
√ 1 1 2x
= −2 cos u + C = −2 cos x + c = dx + dx
1 + x2 2 1 + x2
1 1 1
22. Let u = , du = − 2 dx = tan−1 x + ln |1 + x2 | + c
x x 2
cos(1/x)
dx = − cos udu 1
x2 34. √ dx
1 x+x
= − sin u + C = − sin + c
x 1
= x−1/2 · dx
23. Let u = sin x, du = cos xdx 1 + x1/2
π 0
= 2 ln | 1 + x1/2 | + c
cos xesin x dx = eu du = 0
0 0
ln x2 1
2 35. dx = 2 ln x dx
24. Let u = tan x, du = sec xdx x x
π/2 1 1
sec2 xetan x dx = eu du Let u = ln x, du = dx.
x
0 0
2
u
1
=2 u du = u2 + c = (ln x) + c
=e =e−1
0
3 3 3
0 x3 26
25. sec x tan xdx 36. e2 ln x dx = x2 dx = =
−π/4 1 1 3 1 3
0 √ 4
= sec x =1− 2 √
−π/4 37. x x − 3dx
3
π/2 4 √
π/2
26. csc2 xdx = − cot x =1 = (x − 3 + 3) x − 3dx
π/4 π/4 3
4 4
3 2 = (x − 3)3/2 dx + 3 (x − 3)1/2 dx
27. Let u = x , du = 3x dx 3 3
x2 1 1 2
4
2
4
12
dx = du = (x − 3)5/2 + 3 · (x − 3)3/2 =
1 + x6 3 1 + u2 5 3 5
3 3
1 1
= tan−1 u + C = tan−1 x3 + c 1
3 3 38. x(x − 3)2 dx
0
x5 1 1
28. dx = ln(1 + x6 ) + c = (x3 − 6x2 + 9x)dx
1 + x6 6
0
1
1 x x4 9 11
29. √ dx = sin−1 + c = − 2x3 + x2 =
4−x 2 2 4 2 0 4

362 CHAPTER 6. INTEGRATION TECHNIQUES

4 2
x2 + 1
39. √ dx 47. f (x)dx
1 x 0
4 4 1 2
x x2
= x3/2 dx + x−1/2 dx = 2+1
dx + dx
1 1 0 x 1 x2 + 1
1 2
4 1 1
2 5/2 4 72 = ln |x2 + 1| + 1− 2 dx
= x + 2x1/2 = 2 0 1 x +1
5 1 1 5 1 2
= ln 2 + (x − arctan x)
0 0
2 1
2 1 −x2 e−4 − 1 ln 2 π
40. xe−x dx = − e = = + 1 + − arctan 2
−2 2 −2 2 2 4
4x + 1
5 5 x 48. dx
41. dx = √ arctan √ + c 2x2 + 4x + 10
3 + x2 3 3
5 4x + 4 3
dx: N/A = 2 + 4x + 10
dx − 2 + 4x + 10
dx
3 + x3 2x 2x
3 1
= ln |2x2 + 4x + 10| − dx
1 2 (x + 1)2 + 4
42. sin(3x)dx = sin(3x)3dx
3 3 x+1
Let u = 3x, du = 3dx. = ln |2x2 + 4x + 10| − tan−1 +c
1 1 4 2
= (sin u)du = − cos u + c
3 3 1
1 49. dx = tan−1 (x) + c.
= − cos(3x) + c. (1 + x2 )
3 x 1 2x
2)
dx = dx
(1 + x 2 (1 + x2 )
sin3 xdx = (sin2 x) sin xdx 1
= ln 1 + x2 + c.
2
= (1 − cos2 x)sin xdx x2 x2 + 1 − 1
dx = dx
Let u = cos x, du = − sin xdx. (1 + x2 ) (1 + x2 )
2
= 1 − u2 (−du) = u2 du − du x +1 1
= 2 + 1)
dx − dx
(x (1 + x2 )
u3 cos3 x 1
= −u= − cos x. = dx − dx
3 3 (1 + x2 )
= x − tan−1 (x) + c.
43. ln xdx: N/A x3 1 x2
2)
dx = 2xdx
Substituting u = ln x, (1 + x 2 (1 + x2 )
ln x 1
dx = ln2 x + c Let u = x2 , du = 2xdx.
2x 4 1 u 1 u+1−1
= du = du
2 1+u 2 1+u
44. Substituting u = x4 1 u+1 1
= du − du
x3 1 2 1+u 1+u
dx = arctan x4 + c
1 + x8 4 1 1
= du − du
x4 2 1+u
dx: N/A 1
1 + x8 = (u − ln (1 + u)) + c
2
1 1
45. e−x dx: N/A
2
= x2 − ln 1 + x2 + c.
2 2
Substituting u = −x2 Hence we can generalize this as follows,
2 1 2 xn
xe−x dx = − e−x + c 1 + x2
dx
2
1 xn−2
= xn−1 − dx
46. sec xdx: N/A n−1 1 + x2
x 1 1
sec2 xdx = tan x + c 50. dx = 2xdx
1 + x4 2 1 + x4

6.2. INTEGRATION BY PARTS 363

Let u = x2 , du = 2xdx. 1 2x 1 2x
xe2x dx =xe − e dx
1 1 1 2 2
= du = tan−1 (u) + c 1 1
2 1 + u2 2 = xe2x − e2x + c.
1 2 4
= tan−1 x2 + c.
2 4. Let u = ln x, dv = x dx
x3 1 1 1 x2
4
dx = 4x3 dx du = dx and v = .
1+x 4 1 + x4 x 2
Let u = 1 + x4 , du = 4x3 . 1 1
x ln x dx = x2 ln x − x dx
1 1 1 2 2
= du = ln (u) + c 1 1
4 u 4 = x2 ln x − x2 + c.
1 2 4
= ln 1 + x4 + c.
4 5. Let u = ln x, dv = x2 dx
x5 1 1
dx du = dx, v = x3 .
1 + x4 x 3
1 x4 2 1 3 1 3 1
= 2xdx x ln xdx = x ln x − x · dx
2 1 + x4 3 3 x
Let u = x2 , du = 2xdx. 1 3 1
= x ln x − x2 dx
1 u2 1 u2 + 1 − 1 3 3
= du = du 1 1
2 1+u 2 2 1 + u2 = x3 ln x − x3 + c.
1 u2 + 1 1 3 9
= du − du
2 1 + u2 1 + u2 1
6. Let u = ln x, du = dx.
1 1 x
= du − du ln x u2 1
2 1 + u2 dx = udu = + c = (ln x)2 + c.
1 x 2 2
= u − tan−1 (u) + c
2
1 2 7. Let u = x2 , dv = e−3x dx
= x − tan−1 x2 + c. 1
2 du = 2xdx, v = − e−3x
Hence we can generalize this as follows, 3
x4n+1 1 x2n−2 x4(n−1)+1 I = x2 e−3x dx
dx = − dx
1 + x4 2 n−1 1 + x4 1 1
and = − x2 e−3x − − e−3x · 2xdx
3 3
x4n+3 1 x2n x4(n−1)+3 1 2
dx = − dx = − x2 e−3x + xe−3x dx
1+x 4 4 n 1 + x4 3 3
Let u = x, dv = e−3x dx
1
6.2 Integration by Parts du = dx, v = − e−3x
3
1
I = − x2 e−3x
1. Let u = x, dv = cos xdx 3
du = dx, v = sin x. 2 1 1
+ − xe−3x − − e−3x dx
x cos xdx = x sin x − sin xdx 3 3 3
1 2 2
= x sin x + cos x + c = − x2 e−3x − xe−3x + e−3x dx
3 9 9
1 2 2 −3x
2. Let u = x, dv = sin 4xdx = − x2 e−3x − xe−3x − e +c
1 3 9 27
du = dx, v = − cos 4x
4 8. Let u = x3 , du = 3x2 dx.
3 1 1
x sin 4x dx x2 ex dx = eu dx = eu + c
3 3
1 1 1 x3
= − x cos 4x − − cos 4x dx = e + c.
4 4 3
1 1
= − x cos 4x + sin 4x + c.
4 16 9. Let I = ex sin 4xdx
3. Let u = x, dv = e2x dx u = ex , dv = sin 4xdx
1 1
du = dx, v = e2x . du = ex dx, v = − cos 4x
2 4


1 1 1
I = − ex cos 4x − − cos 4x ex dx du = cos xdx v = − cos 2x
4 4 2
1 x 1 1 1 1
= − e cos 4x + x
e cos 4xdx I = cos x sin 2x + − cos 2x sin x
4 4 2 2 2
1
Use integration by parts again, this time let − − cos 2x cos xdx
u = ex , dv = cos 4xdx 2
1 1 1 1
du = ex dx, v = sin 4x = cos x sin 2x − cos 2x sin x + Idx
4 2 4 4
1 x
I = − e cos 4x So,
4 3 1 1
1 1 x 1 I = cos x sin 2x − cos 2x sin x + c1
+ e sin 4x − (sin 4x)ex dx 4 2 4
4 4 4
1 1 1 2 1
I = − ex cos 4x + ex sin 4x − I I = cos x sin 2x − cos 2x sin x + c
4 16 16 3 3
So,
17 1 1 12. Here we use the trigonometric identity:
I = − ex cos 4x + ex sin 4x + c1 sin 2x = 2 sin x cos x.
16 4 16
4 1 We then make the substitution
I = − ex cos 4x + ex sin 4x + c
17 17 u = sin x, du = cos x dx.
10. Let, u = e2x , dv = cos x dx so that, sin x sin 2x dx = 2 sin2 x cos x dx
du = 2e2x dx and v = sin x.
e2x cos x dx 2 3 2
= 2u2 du = u + c = sin3 x + c
3 3
= e2x sin x − 2 e2x sin x dx This integral can also be done by parts, twice.
If this is done, an equivalent answer is ob-
Let, u = e2x , dv = sin x dx so that, tained:
du = 2e2x dx and v = − cos x. 1 2
cos x sin 2x − cos 2x sin x + c
e2x sin x dx 3 3
13. Let u = x, dv = sec2 xdx
2x 2x
= −e cos x + 2 e cos x dx du = dx, v = tan x

e2x cos x dx x sec2 xdx = x tan x − tan xdx
sin x
= e2x sin x + 2e2x cos x − 4 e2x cos x dx = x tan x − dx
cos x
Now we notice that the integral on both of Let u = cos x, du = − sin xdx
1
these is the same, so we bring them to one side x sec2 xdx = x tan x + du
of the equation. u
= x tan x + ln |u| + c
5 e2x cos x dx = x tan x + ln |cos x| + c

= e2x sin x + 2e2x cos x + c1 14. Let u = (ln x)2 , dv = dx
ln x
e2x cos x dx du = 2 dx, v = x
x
1 2x 2
= e sin x + e2x cos x + c I = (ln x)2 dx
5 5
ln x
= x(ln x)2 − x·2 dx
11. Let I = cos x cos 2xdx x
and u = cos x, dv = cos 2xdx = x(ln x)2 − 2 ln xdx
1
du = sin xdx, v = sin 2x Integration by parts again,
2 1
1 1 u = ln x, dv = dxdu = dx, v = x
I = cos x sin 2x − sin 2x(− sin x)dx x
2 2 1
2
1 1 I = x(ln x) − 2 x ln x − x · dx
= cos x sin 2x + sin x sin 2xdx x
2 2
Let,u = sin x, dv = sin 2xdx = x(ln x)2 − 2x ln x + 2 dx


= x(ln x)2 − 2x ln x + 2x + c 20. Let u = 2x, dv = cos x dx
duπ= 2 dxandv = sin x. π
2
15. Let u = x2 , dv = xex dx so that, du = 2x dx 2x cos xdx = 2x sin x|0 − 2
π
sin xdx
1 2 0 0
and v = ex (v is obtained using substitu- = (2x sin x +
π
2 cos x)|0 = −4.
2
tion).
2 1 2 2 1
x3 ex dx = x2 ex − xex dx 21. x2 cos πxdx
2
0
1 2 1 2
= x2 ex − ex + c Let u = x2 , dv = cos πxdx,
2 2 sin πx
du = 2xdx, v = .
π
x 1 1 1
16. Let u = x2 , dv = dx sin πx sin πx
3/2 x2 cos πxdx = x2 − 2xdx
(4 + x2 ) 0 π 0 0 π
1 2 1
du = 2xdx, v = − √ = (0 − 0) − x sin (πx) dx
4 + x2 π 0
3 1
x x 2
3/2
dx = x2 3/2
dx =− x sin (πx) dx
(4 + x2 ) (4 + x2 ) π 0
x2 1 Let u = x, dv = sin(πx)dx,
= −√ + √ 2xdx cos(πx)
4+x 2 4 + x2 du = dx, v = − .
x2 π
1
=− + 2 (4 + x2 ) + c. 2
(4 + x2 ) − xsin(πx)dx
π 0
1 1
17. Let u = ln(sin x), dv = cos xdx 2 x cos(πx) cos(πx)
=− − − − dx
1 π π 0 0 π
du = · cos xdx, v = sin x 1
sin x 2 cos π 1 sin(πx)
=− (− − 0) +
I = cos x ln(sin x)dx π π π π 0
= sin x ln(sin x) 2 1 1 2
1 =− + (0 − 0) = − 2
− sin x · · cos xdx π π π π
sin x
1
= sin x ln(sin x) − cos xdx
22. x2 e3x dx
= sin x ln(sin x) − sin x + c 0
Let u = x2 , dv = e3x dx,
e3x
18. This is a substitution u = x2 . du = 2xdx, v = .
1 3
x sin x2 dx = sin udu 1
x2 e3x
1 1 3x
e
2 x2 e3x dx = − 2xdx
1 1 3 0 3
= − cos u + c = − cos x2 + c. 0 0
2 2 1 3 2 1 3x
= e −0 − xe dx.
19. Let u = x, dv = sin 2xdx 3 3 0
1 Let u = x, dv = e3x dx,
du = dx, v = − cos 2x e3x
2 dv = dx, v = .
1
3
x sin 2xdx e3 2 1 3x
0 − xe dx
1
1
1
1 3 3 0
= − x cos 2x − − cos 2x dx e3 2 e3x
1 1 3x
e
2 0 0 2 = − x − dx
1 1 1 3 3 3 0 0 3
= − (1 cos 2 − 0 cos 0) + cos 2xdx 1
2 2 0 e3 2 e3 e3x
1 = − − dx
1 1 1 3 3 3 0 3
= − cos 2 + sin 2x 3 1
2 2 2 0 e 2 e3 e3x
1 1 = − −
= − cos 2 + (sin 2 − sin 0) 3 3 3 9 0
2 4 e 3
2 e3 1 3
1 1 = − − e −1
= − cos 2 + sin 2 3 3 3 9
2 4


e3 2e3 2 3 x cos (ax) sin (ax)
= − + e −1 =− + + c, a = 0.
3 9 27 a a2
e3 2e3 2e3 2 5e3 2
= − + − = −
3 9 27 27 27 27 27. (xn ) (ln x) dx = (ln x) (xn ) dx
10
Let u = ln x, dv = xn dx,
23. ln 2xdx 1 xn+1
1 du = dx, v = .
Let u = ln 2x, dv = dx x (n + 1)
1
du = dx, v = x. (ln x)(xn ) dx
x
10 10
10 1 xn+1 xn+1 dx
ln (2x)dx = x ln (2x)|1 − x dx = (ln x) −
1 1 x (n + 1) (n + 1) x
10
= (10 ln(20) − ln 2) − dx xn+1 (ln x) xn
= − dx
1
10
(n + 1) (n + 1)
= (10 ln(20) − ln 2) − [x]1 x n+1
(ln x) x n+1
= (10 ln(20) − ln 2) − (10 − 1) = − 2 + c, n = −1.
(n + 1) (n + 1)
= (10 ln(20) − ln 2) − 9.

24. Let, u = ln x, dv = x dx
28. (sin ax) (cos bx) dx
1 x2
du = dx, v = .
x 2 Let u = sin ax, dv = (cos bx) dx
2 2 2 sin bx
1 1 du = a (cos ax) dx, v = .
x ln xdx = x2 ln x − xdx b
1 2 1 1 2
2
1 2 1 3 sin ax cos bx dx
= x ln x − x2 = 2 ln 2 − .
2 4 1 4 sin bx sin bx
= (sin ax) − a (cos ax) dx
b b
25. x2 eax dx (sin ax) (sin bx) a
= − (cos ax) (sin bx) dx
b b
Let u = x2 , dv = eax dx, Let u = cos ax, dv = sin bxdx,
eax cos bx
du = 2xdx, v = . du = −a (sin ax) dx, v = − .
aax b
e eax
x2 eax dx = x2 − 2xdx sin ax sin bx a
a a − cos ax sin bx dx
b b
x2 eax 2 sin ax sin bx a − cos bx
= − xeax dx. = − cos ax
a a b b b
Let u = x, dv = eax dx,
eax − cos bx
dv = dx, v = . − (− sin ax) adx
a b
2 ax
x e 2 sin ax sin bx a − cos ax cos bx
− xeax dx = −
a a b b b
x2 eax 2 eax eax a
= − x − dx − cos bx sin ax dx
a a a a b
x2 eax 2 xeax eax sin ax sin bx a cos ax cos bx
= − − 2 +c = +
a a a a b b2
a 2
x2 eax 2xeax 2eax + sin ax cos bx dx
= − + 3 + c, a = 0. b
a a2 a
sin ax cos bx dx
26. x sin (ax) dx sin ax sin bx a cos ax cos bx
= +
Let u = x, dv = sin axdx, b b2
cos ax a 2
du = dx, v = − . + sin ax cos bx dx
a b
a 2
xsin (ax) dx sin ax cos bx dx − sin ax cos bx dx
b
− cos (ax) cos (ax) sin ax sin bx a cos ax cos bx
=x − − dx = +
a a b b2


a2
1− sin ax cos bx dx + (n − 1) sinn xdx
b2
sin ax sin bx a cos ax cos bx n sinn xdx
= +
b b2
= − sinn−1 x cos x
sin ax cos bx dx
− (n − 1) sinn−2 xdx
b2 sin ax sin bx a cos ax cos bx
= + 1
b2 − a2 b b2 sinn xdx = − sinn−1 x cos x
n
sin ax cos bx dx n−1
− sinn−2 xdx
1 n
= 2 − a2
(b sin ax sin bx + a cos ax cos bx) ,
b
a = 0 b = 0. 31. x3 ex dx = ex (x3 − 3x2 + 6x − 6) + c
29. Letu = cosn−1 x, dv = cos xdx
du = (n − 1)(cosn−2 x)(− sin x)dx, v = sin x 32. cos5 xdx
cosn xdx 1 4
= cos4 sin x + cos3 xdx
= sin x cos n−1
x 5 5
1
− (sin x)(n − 1)(cosn−2 x)(− sin x)dx = cos4 sin x
5
= sin x cosn−1 x 4 1 2
+ cos2 x sin x + cos xdx
5 3 3
+ (n − 1)(cosn−2 x)(sin2 x)dx 1 4
= cos4 sin x + cos2 x sin x
= sin x cosn−1 x 5 15
8
+ (n − 1)(cosn−2 x)(1 − cos2 x)dx + sin x + c
15
= sin x cosn−1 x
+ (n − 1)(cosn−2 x − cosn x)dx 33. cos3 xdx
1 2
Thus, cosn xdx = cos2 x sin x + cos xdx
3 3
1 2
= sin x cosn−1 x + (n − 1) cosn−2 xdx = cos2 x sin x + sin x + c
3 3
− (n − 1) cosn xdx. 34. sin4 xdx
n cosn xdx = sin x cosn−1 x 1
= − sin3 x cos x +
3
sin2 xdx
4 4
+ (n − 1) cosn−2 xdx 1 3 1 1
= − sin3 x cos x + x − sin 2x
4 4 2 4
cosn xdx
1
1 n−1 35. x4 ex dx
= sin x cosn−1 x + cos n−2
xdx 0
n n 1
= ex (x4 − 4x3 + 12x2 − 24x + 24) 0
30. Let u = sinn−1 x, dv = sin x dx = 9e − 24
du = (n − 1) sinn−2 x cos x, v = − cos x.
sinn xdx 36. Using the work done in Exercise 34,
π/2

= − sinn−1 x cos x sin4 xdx
0
+ (n − 1) cos2 x sinn−2 xdx 1 3 3
π/2
= − sin3 x cos x + x − sin 2x
= − sinn−1 x cos x 4 8 16 0
3π
+ (n − 1) (1 − sin2 x) sinn−2 xdx =
16
= − sinn−1 x cos x π/2
− (n − 1) sinn−2 xdx 37. sin5 xdx
0


π/2 π/2
1 4 π/2 3
= − sin4 x cos x + sin xdx cosm xdx
5 0 5 0 0
1
π/2 (n − 1)(n − 3)(n − 5) · · · 2
= − sin4 x cos x = .
5 n(n − 2)(n − 4) · · · 3
0
π/2
4 1 2 41. Let u = cos−1 x, dv = dx
+ − sin2 x cos x − cos x 1
5 3 3 0 du = − √ dx, v = x
(Using Exercise 30) 1 − x2
1 π π cos−1 xdx
=− sin4 cos − sin4 0 cos 0 I=
5 2 2
4 1 2 π π 2 π 1
+ − sin cos − cos = x cos−1 x − x −√ dx
5 3 2 2 3 2 1 − x2
8 x
= = x cos−1 x + dx √
15 1 − x2
Substituting u = 1 − x2 , du = −2xdx
38. Here we will again use the work we did in Ex-
1 1
ercise 34. I = x cos−1 x + √ − du
u 2
sin6 xdx 1
= x cos1 x − u−1/2 du
1 5 2
= − sin5 x cos x + sin4 xdx 1
6 6 = x cos−1 x − · 2u1/2 + c
1 2
= − sin5 x cos x = x cos−1 x − 1 − x2 + c
6
5 1 3 3
+ − sin3 x cos x + x − sin 2x + c 42. Let u = tan−1 x, dv = dx
6 4 8 16 1
1 5 du = dx, v = x
= − sin5 x cos x − sin3 x cos x 1 + x2
6 24 x
15
+ x−
15
sin 2x + c I= tan−1 xdx = x tan−1 x − dx
48 96 1 + x2
Substituting u = 1 + x2 ,
We now just have to plug in the endpoints: 1
π/2 I = x tan−1 x − ln(1 + x2 ) + c.
sin6 xdx 2
0 √ 1
1 5 43. Substituting u = x, du = √ dx
= − sin5 x cos x − sin3 x cos x 2 x
6 24 √
π/2 I = sin xdx = 2 u sin udu
15 15
+ x− sin 2x
48 96 0 = 2(−u cos u + sin u) + c
√ √ √
15π = 2(− x cos x + sin x) + c
=
96 √
44. Substituting w = x
39. m even : 1 1
π/2 dw = √ dx = dx
sinm xdx 2 x 2w
√
x
0
(m − 1)(m − 3) . . . 1 π I= e dx = 2wew dx
= · Next, using integration by parts
m(m − 2) . . . 2 2
m odd: u = 2w, dv = ew dw
π/2
du = 2dw, v = ew
sinm xdx
0 I = 2wew − 2 ew dw
(m − 1)(m − 3) . . . 2 √ √ √
=
m(m − 2) . . . 3 = 2wew − 2ew + c = 2 xe x − 2e x + c

40. m even: 45. Let u = sin(ln x), dv = dx
π/2 dx
cosm xdx du = cos(ln x) , v = x
0
x
π(n − 1)(n − 3)(n − 5) · · · 1 I = sin(ln x)dx
=
2n(n − 2)(n − 4) · · · 2
m odd: = x sin(ln x) − cos(ln x)dx


Integration by parts again, = 3 u2 eu − 2 ueu du
u = cos(ln x), dv = dx
dx
du = − sin(ln x) , v = x = 3u2 eu − 6 ueu − eu du
x
cos(ln x)dx = 3u2 eu − 6ueu + 6eu + c
8 √ 2
3 x
Hence e dx = 3u2 eu du
= x cos(ln x) + sin(ln x)dx 0 0
2
I = x sin(ln x) − x cos(ln x) − I = 3u e − 6ueu + 6e
2 u u
0
= 6e2 − 6
2I = x sin(ln x) − x cos(ln x) + c1
1 1 50. Let u = tan−1 x, dv = xdx
I = x sin(ln x) − x cos(ln x) + c dx x2
2 2 du = , v=
1 + x2 2
46. Let u = 4 + x2 , du = 2xdx I= x tan−1 xdx
I= x ln(4 + x2 )dx x2 1 x2
= tan−1 x − dx
1 1 2 2 1 + x2
= ln udu = (u ln u − u) + C x2
2 2 = tan−1 x
1 2
= [(4 + x ) ln(4 + x2 ) − 4 − x2 ] + c
2
1 1
2 − 1dx − dx
2 1 + x2
47. Let u = e2x , du = 2e2x dx x2 1
1 = tan−1 x − x − tan−1 x + C
I = e6x sin(e2x )dx = u2 sin udu 2 2
2 −1 x
2
x 1
Let v = u2 , dw = sin udu = tan x − + tan−1 x + c
2 2 2
dv = 2udu, w = − cos u 1
1 Hence x tan−1 xdx
I= −u2 cos u + 2 u cos udu 0
2 x2 x 1
1
π 1
1 = tan−1 x − + tan−1 x = −
= − u2 cos u + u cos udu 2 2 2 0 4 2
2
1 2 51. n times. Each integration reduces the power of
= − u cos u + (u sin u + cos u) + c
2 x by 1.
1
= − e4x cos(e2x ) + e2x sin(e2x )
2 52. 1 time. The first integration by parts gets rid
+ cos(e2x ) + c of the ln x and turns the integrand into a sim-
ple integral. See, for example, Problem 4.
√ 1 −2/3
48. Let u = 3
x = x1/3 , du = x dx, 53. (a) As the given problem, x sin x2 dx can
3 be simplified by substituting x2 = u, we
3u2 du = dx
can solve the example using substitution
I = cos x1/3 dx = 3 u2 cos udu method.
Let v = u2 , dw = cos udu (b) As the given integral, x2 sin x dx can not
dv = 2udu, w = sin u be simplified by substitution method and
I = 3 u2 sin u − 2 u sin udu can be solved using method of integration
by parts.
= 3u2 sin u − 6 u sin udu (c) As the integral, x ln x dx can not be sim-
plified by substitution and can be solved
= 3u2 sin u − 6 −u cos u + cos udu using the method of integration by parts.
3 ln x
= 3u sin u + 6u√ u −√ sin u + c √
√ cos 6 (d) As the given problem, dx can be
= 3x sin 3 x + 6 3 x cos 3 x − 6 sin 3 x + c x
simplified by substituting , ln x = u we
√ 1 −2/3 can solve the example by substitution
49. Let u = 3
x = x1/3 , du = x dx, method.
3
3u2 du = dx
√
3 54. (a) As this integral, x3 e4x dx can not be
I = e x dx = 3 u2 eu du simplified by substitution method and can


be solved by using the method of integra- 59.
tion by parts. e2x
4 4 2x
(b) As the given problem, x3 ex dx can be x e /2 +
simplified by substituting x4 = u, we can 4x3 e2x /4 −
solve the example using the substitution 12x2 e2x /8 +
2x
method. 24x e /16 −
4 24 e2x /32 +
(c) As the given problem, x−2 e x dx can be
1
simplified by substituting = u, we can x4 e2x dx
x
solve the example using the substitution x4 3x2 3x 3
= − x3 + − + e2x + c
method. 2 2 2 4
(d) As this integral, x2 e−4x dx can not be 60.
simplified by substitution and can be cos 2x
solved by using the method of integration x 5
sin 2x/2 +
by parts.
5x4 − cos 2x/4 −
55. First column: each row is the derivative of the 20x3 − sin 2x/8 +
previous row; Second column: each row is the 60x2 cos 2x/16 −
antiderivative of the previous row. 120x sin 2x/32 +
120 − cos 2x/64 −
56.
sin x
4 x5 cos 2xdx
x − cos x +
4x3 − sin x − 1 5 5
= x sin 2x + x4 cos 2x
12x2 cos x + 2 4
24x sin x − 20 60
− x3 sin 2x − x2 cos 2x
24 − cos x + 8 16
120 120
x4 sin xdx + x sin 2x + cos 2x + c
32 64
= −x4 cos x + 4x3 sin x + 12x2 cos x 61.
− 24x sin x − 24 cos x + c e−3x
3 −3x
57. x −e /3 +
cos x 3x2 e−3x /9 −
x4 sin x + 6x −e−3x /27 +
4x3 − cos x − 6 e−3x /81 −
12x2 − sin x +
x3 e−3x dx
24x cos x −
24 sin x + x3 x2 2x 2
= − − − − e−3x + c
3 3 9 27
x4 cos xdx
62.
= x4 sin x + 4x3 cos x − 12x2 sin x x2
− 24x cos x + 24 sin x + c ln x x3 /3 +
−1
58. x x4 /12 +
ex −x −2
x5 /60 +
4
x ex + The table will never terminate.
4x3 ex −
12x2 ex + 63. (a) Use the identity
24x ex − cos A cos B
1
24 ex + = [cos(A − B) + cos(A + B)]
2
x4 ex dx This identity gives
π
4 3 2
= (x − 4x + 12x − 24x + 24)e + c x cos(mx) cos(nx)dx
−π


π nπ
1 1
= [cos((m − n)x) = cos2 udu
−π 2 n −nπ
+ cos((m + n)x)]dx nπ
1 1 1
1 sin((m − n)x) = u + cos(2u) =π
= n 2 4 −nπ
2 m−n π
π And then sin2 (nx)dx
sin((m + n)x) −π
+ π
m+n −π = (1 − cos2 (nx))dx
=0 −π
π π
It is important that m = n because oth- = dx − cos2 (nx)dx
erwise cos((m − n)x) = cos 0 = 1 −π −π

(b) Use the identity = 2π − π = π
sin A sin B
1 65. The only mistake is the misunderstanding of
= [cos(A − B) − cos(A + B)]
2 antiderivatives. In this problem, ex e−x dx
This identity gives
π is understood as a group of antiderivatives of
sin(mx) sin(nx)dx ex e−x , not a ﬁxed function. So the subtraction
−π
π
1 by ex e−x dx on both sides of
= [cos((m − n)x)
−π 2
ex e−x dx = −1 + ex e−x dx
− cos((m + n)x)]dx
1 sin((m − n)x) does not make sense.
= π √ π
2 m−n
π
66. V = π (x sin x)2 dx = π x2 sin xdx
sin((m + n)x) 0 0
−
m+n −π
Using integration by parts twice we get
=0 x2 sin xdx
It is important that m = n because oth-
erwise cos((m − n)x) = cos 0 = 1 = −x2 cos x + 2 x cos xdx

64. (a) Use the identity = −x2 cos x + 2(x sin x − sin xdx)
cos A sin B = −x2 cos x + 2x sin x + 2 cos x + c
1
= [sin(B + A) − sin(B − A)] Hence,
2 π
This identity gives V = (−x2 cos x + 2x sin x + 2 cos x) 0
π = π 2 − 4 ≈ 5.87
cos(mx) sin(nx) dx
−π
π
1 67. Let u = ln x, dv = ex dx
= [sin((n + m)x) dx
−π 2 du = , v = ex
x
− sin((n − m)x)] dx ex
ex ln xdx = ex ln x − dx
1 cos((n + m)x) x
= − ex
2 n+m ex ln xdx + dx = ex ln x + C
π x
cos((n − m)x) Hence,
+
n−m 1
−π ex ln x + dx = ex ln x + c
=0 x
(b) We have seen that 68. We can guess the formula:
1 1
cos2 xdx = x + cos(2x) + c ex (f (x) + f (x))dx = ex f (x) + c
2 4
Hence by letting u = nx: and prove it by taking the derivative:
π
cos2 (nx)dx d x
(e f (x)) = ex f (x) + ex f (x)
−π dx


b
= ex (f (x) + f (x)) + f (x) (b − x) dx
a
1 b
69. Consider, f (x)g (x) dx Consider x sin (b − x) dx
0 0
Choose u = g (x) and dv = f (x)dx, b b

so that du = g (x) dx and , v = f (x) . = (b − x) sin xdx = (sin x) (b − x) dx
0 0
Hence, we have Now, consider
1
g (x)f (x)dx f (x) = x − sin x ⇒ f (x) = 1 − cos x
0 and f (x) = sin x.
1
1
= g (x) f (x)|0 − f (x)g (x) dx Therefore, using
0 f (b) = f (a) + f (a) (b − a)
= (g (1) f (1) − g (0) f (0)) b
1 + f (x) (b − x) dx,
− g (x)f (x) dx a
0 we get
From the given data. b − sin b = 0 − sin 0 + f (0) (b − 0)
1
b
= (0 − 0) − g (x)f (x) dx. + (sin x) (b − x) dx
0
0
Choose, u = g (x) and dv = f (x)dx, b
so that,du = g (x) dx and v = f (x) . ⇒ |sin b − b| = x sin (b − x) dx .
0
Hence, we have
1 Further,
− g (x)f (x) dx b b
0 |sin b − b| = x sin (b − x) dx ≤ xdx ,
1 0 0
1
=− g (x) f (x)|0 − f (x) g (x) dx as sin (b − x) ≤ 1.
0
= − {(g (1) f (1) − g (0) f (0) ) b2
Thus, |sin b − b| ≤ .
1 2
− f (x) g (x) dx Therefore the error in the approximation
0 1
From the given data. sin x ≈ x is at most x2 .
1 2
= − (0 − 0 ) − f (x) g (x) dx
1
0
6.3 Trigonometric
= f (x) g (x) dx.
0
Techniques of
70. Consider, Integration
b b
f (x) (b − x) dx = (b − x) f (x) dx 1. Let u = sin x, du = cos xdx
a a
Choose u = (b − x) and dv = f (x) dx, cos x sin4 xdx = u4 du
so that du = −dx and v = f (x) . 1 5 1
= u + c = sin5 x + c
Hence, we have: 5 5
b
(b − x)f (x) dx 2. Let u = sin x, du = cos xdx
a
b cos3 x sin4 xdx = (1 − u2 )u4 du
b
= (b − x) f (x)|a + f (x) dx
a u5 u7
b = − +c
5 7
= (0 − [(b − a) f (a)]) + f (x) dx sin x sin7 x
5
a
b
= − +c
= − [(b − a) f (a)] + f (x)|a 5 7
= − [(b − a) f (a)] + f (b) − f (a) 3. Let u = sin 2x, du = 2 cos 2xdx.
b π/4
f (x) (b − x) dx cos 2xsin3 2xdx
a 0
= − [(b − a) f (a)] + f (b) − f (a) 1 1
1 1 u4 1
= u3 du = =
f (b) = f (a) + (b − a) f (a) 2 0 2 4 0 8

6.3. TRIGONOMETRIC TECHNIQUES OF INTEGRATION 373

4. Let u = cos 3x, du = −3 sin xdx. =− cot x(1 + cot2 x) · csc2 xdx
π/3
cos3 3x sin3 3x dx u2 u4
π/4 =− (u + u3 )du = − − +C
−1 2 4
1
=− √ u
3
1− u2 du cot2 x cot4
3 −1/ 2 =− − +c
2 4
4 6 −1
1 u u
=− − 11. Let u = x2 + 1, so that du = 2xdx.
3 4 6 −1
√
2
1 3 7 1 xtan3 x2 + 1 sec x2 + 1 dx
=− − =−
3 16 48 72 1
= tan3 u (sec u) du
5. Let u = cos x, du = − sin xdx 2
π/2 0 1
= sec2 u − 1 tan u (sec u) du
cos2 x sin xdx = u2 (−du) 2
0 1 Let sec u = t, dt = tan u sec udu
0
1 1 1 1 t3
= − u3 = = t2 − 1 dt = −t +c
3 1 3 2 2 3
1 sec3 u
6. Let u = cos x, du = − sin xdx = − sec u + c
0 1 2 3
cos3 x sin xdx = − u3 du = −1 1 1
−π/2 0 = sec3 x2 + 1 − sec x2 + 1 + c.
6 2

7. cos2 (x + 1) dx 12. Let u = 2x + 1, so that du = 2dx.
1 tan (2x + 1) .sec3 (2x + 1) dx
= (1 + cos 2 (x + 1))dx
2 1
1 1 = tan u. sec u.sec2 udu
= x + (sin 2 (x + 1)) + c. 2
2 4 1
= sec2 utan u sec udu
8. Let u = x − 3, du = dx 2
Let t = sec u, so that dt = tan u sec udu.
sin4 (x − 3)dx = sin4 udu 1 1 t3
= t2 dt = +c
2 2 2 3
= sin2 u du
1 sec3 u 1
(1 − cos 2u) (1 − cos 2u) = + c = sec3 (2x + 1) + c.
= × du 2 3 6
2 2
1 13. Let u = cot x, du = −csc2 x dx
= 1 − 2 cos 2u + cos2 2u
4
1 1 cot2 x csc4 xdx = cot2 x 1 + cot2 x csc2 xdx
= 1 − 2 cos 2u + (1 + cos 4u) du
4 2
=− u2 1 + u2 du
3 1 1
= u − sin 2u + cos 4u + c u3 u5
8 4 32 =− − +c
3 1 3 5
3 5
= (x − 3) − sin 2 (x − 3) (cot x) (cot x)
8 4 =− − + c.
1 3 5
+ cos 4 (x − 3) + c.
32
14. Let u = cot x, du = −csc2 x dx.
9. Let u = sec x, du = sec x tan xdx
3
cot2 x csc2 xdx = − u2 du
tan x sec xdx
u3 cot3 x
2
=− +c= + c.
= tan x sec x sec xdx 3 3
1 3 1 15. Let u = tan x, du = sec2 xdx
= u2 du = u + c = sec3 x + c π/4
3 3
tan4 x sec4 xdx
2
10. Let u = cot x, du = − csc xdx 0
π/4
cot x csc4 xdx = tan4 x sec2 x sec2 xdx
0


π/4 π π
21. Let x = 3 sin θ, − < θ <
= tan4 x(1 + tan2 x) sec2 xdx 2 2
0 dx = 3 cos θ dθ
1 1 3 cos θ
= u4 (1 + u2 ) du √ dx = dθ
0 x 2 9 − x2 9 sin2 θ · 3 cos θ
1
u5 u7
1
12 1 1
= (u4 + u6 )du = + = = csc2 θdθ = − cot θ + C
5 7 35 9 9
0 0
By drawing a diagram, √ see that if
we
16. Let u = tan x, du = sec2 xdx. 9 − x2
π/4 x = sin θ, then cot θ = .
x
tan4 x sec2 xdx √
π/4 9 − x2
1 1 Thus the integral = − +c
u5 2 9x
= u4 du = = π π
−1 5 −1 5 22. Let x = 4 sin θ, − < θ < ,
2 2
dx = 4 cos θdθ
17. cos2 x sin2 xdx 1 cos θ
√ dx = dθ
1 1 x 2 16 − x2 16 sin2 θ cos θ
= (1 + cos 2x) · (1 − cos 2x)dx 1 1
2 2 = csc2 θdθ = − cot θ + c
1 16 √ 16
= (1 − cos2 2x)dx 16 − x2
4 =− +c
1 1 16x
= 1 − (1 + cos 4x) dx
4 2 23. Let x = 4sinθ, so that dx = 4 cos θdθ.
1 1 1 x2 16sin2 θ 4 cos θ
= x − sin 4x + c √ dx = dθ
4 2 8 16 − x2 2
1 1 16 − (4 sin θ)
= x− sin 4x + c sin2 θ cos θ
8 32 = 64 dθ
16 − 16sin2 θ
18. (cos2 x + sin2 x)dx = 1dx = x + c sin2 θ cos θ
= 64 dθ
19. Let u = cosx, du = − sin xdx 4 1 − sin2 θ
0 √ sin2 θ cos θ
cos x sin3 xdx = 16 dθ = 16 sin2 θdθ
−π/3 cos θ
0 √ 1 − cos 2θ
= cos x(1 − cos2 x) sin xdx = 16 dθ
2
−π/3
1 √
=8 dθ − (cos 2θ) dθ
= u(1 − u2 )(−du)
1/2 sin 2θ
1 =8 θ− +c
= (u 5/2
−u 1/2
)du 2
x x
1/2
1
= 8sin−1 − 4 sin 2sin−1 + c.
2 7/2 2 3/2 25 √ 8 4 √ 4
= u − u = 2− −1 x x 16 − x2
7 3 1/2 168 21 = 8sin − +c
4 2
20. Let u = cot x, du = − csc2 xdx 24. Let x = 3 sin θ, so that dx = 3 cos θdθ.
π/2 x3
cot2 x csc4 xdx √ dx
π/4 9 − x2
π/2 27 sin3 θ
= cot2 x csc2 x csc2 xdx = (3 cos θ) dθ
2
π/4 9 − (3 sin θ)
π/2
= cot2 x(1 + cot2 x) csc2 xdx sin3 θ
= 81 (cos θ) dθ
π/4
0
9 − 9sin2 θ
=− u2 (1 + u2 )du sin3 θ
= 81 cos θdθ = 27 sin3 θdθ
1 3 cos θ
0
u3 u5 1 1 8 3 sin θ − sin 3θ
=− + = + = = 27 dθ
3 5 1 3 5 15 4


27 Putting all these together and using
= 3 sin θdθ − sin 3θdθ √
4 x x2 − 9
27 cos 3θ sec θ = , tan θ = :
= −3 cos θ + +c 3 3
2
4 3 x
27 x
√ dx = 9 sec3 θ dθ
= −3 cos sin−1 x2 − 9
4 3 9 9
= sec θ tan θ + sec θ dθ
cos sin−1 x 3 2 2
+ + c. 9 9
3 = sec θ tan θ + ln | sec θ + tan θ| + c
2 √ 2
25. This is the area of a quarter of a circle of radius 9 x x2 − 9
2, =
2
2 3 3
√
4 − x2 dx = π 9 x x2 − 9
0 + ln + +c
2 3 3
26. Let u = 4 − x2 , du = −2xdx √ √
1
x 3
du x x2 − 9 9 x + x2 − 9
√ dx = − √ = + ln +c
4−x 2 2 u 2 2 3
0 4
3 √
= −u1/2 = 2 − 3 28. Let u = x2 − 1, du = 2xdx
4

27. Let x = 3 sec θ, dx = 3 sec θ tan θdθ. x3 x2 − 1dx
x2 1
I= √ dx
x2 − 9 = x2 x2 − 1(2x)dx
2
27 sec2 θ sec θ tan θ 1 √
= √ dθ = (u + 1) udu
9 sec2 θ − 9 2
= 9 sec3 θdθ 1
= u3/2 + u1/2 du
2
Use integration by parts. 1 2u5/2 2u3/2
Let u = sec θ and dv = sec2 θdθ. This gives = + +c
2 5 3
sec3 θdθ 1 2 1
= (x − 1)5/2 + (x2 − 1)3/2 + c
5 3
= sec θ tan θ − sec θ tan2 θdθ
29. Let x = 2 sec θ, dx = 2 sec θ tan θdθ
= sec θ tan θ − sec θ(sec2 θ − 1)dθ 2 4 sec θ tan θ
√ dx = dθ
x 2−4 2 tan θ
= sec θ tan θ + sec θdθ − sec3 θdθ =2 sec θdθ
= 2 ln |2 sec θ + 2 tan θ| + c
2 sec3 θdθ
= 2 ln x + x2 − 4 + c
= sec θ tan θ + sec θdθ
30. Let x = 2 sec θ, dx = 2 sec θ tan θdθ
sec3 θdθ x 4 sec2 θ tan θ
√ dx = dθ
1 1 x2 − 4 2 tan θ
= sec θ tan θ + sec θ dθ
2 2 =2 sec2 θdθ = 2 tan θ + C = x2 − 4 + c

This leaves us to compute sec θdθ. √ √
4x2 − 9 4x2 − 9
For this notice if u = sec θ + tan θ then 31. dx = 4xdx
x 4x2
du = sec θ tan θ + sec2 θ.
Let u = 4x2 − 9,
sec θdθ 1 1
du = √ 8xdx = 8xdx
sec θ(sec θ + tan θ) 2 4x2 − 9 2u
= dθ or udu = 4xdx.
sec θ + tan θ
1 Hence, we have
= du = ln |u| + c √
u 4x2 − 9
= ln | sec θ + tan θ| + c dx
x


u u2 √ √
= udu = du = (16 2 tan3 θ)(2 2 sec θ)dθ
u2
+9 u2+9
2
u +9−9 9 = 64 tan3 θ sec θ dθ
= du = du − du
u2 + 9 u2 + 9
u
= u − 9tan−1 +c = 64 (sec2 θ − 1)(sec θ tan θ dθ)
3 √
4x2 − 9 64 3
= 4x 2 − 9 − 9tan−1 + c. = 64 (u2 − 1)du = u − 64u + c
3 3
64
= sec3 θ − 64 sec θ + c
32. Let√ = 2 sec θ, dx = 2 tan θ sec θdθ.
x 3
√ 3 √
x2 − 4 64 8 + x2 8 + x2
dx = √ − 64 √ +c
√x2 3 2 2 2 2
4sec2 θ − 4 √
= (2 tan θ sec θ) dθ 2 2 √
4sec2 θ = (8 + x2 )3/2 − 16 2(8 + x2 )1/2 + c
2 tan θ 3
= (2 tan θ sec θ) dθ
4sec2 θ 35. Let x = 4 tan θ, dx = 4 sec2 θdθ
2
tan θ sec2 θ − 1
= dθ = dθ 16 + x2 dx
sec θ sec θ
1
= sec θdθ − dθ = 16 + 16 tan2 θ · 4 sec2 θdθ
sec θ
= sec θdθ − cos θdθ = 16 sec3 θdθ
= ln |sec θ + tan θ| − sin θ + c 1 1
x x = 16 sec θ tan θ + sec θdθ
= ln sec sec−1 + tan sec−1 2 2
2 2
x = 8 sec θ tan θ + 8 sec θdθ
− sin sec−1 +c
2
x x = 8 sec θ tan θ + 8 ln |sec θ + tan θ| + c
= ln + tan sec−1 1
2 2 = x 16 + x2
x
− sin sec−1 + c. 2
2 1 x
+ 8 ln 16 + x2 + +c
4 4
33. Let x = 3 tan θ, dx = 3 sec2 θdθ
x2 36. Let x = 2 tan θ, dx = 2 sec2 θdθ
√ dx
9 + x2 1 2 sec2 θ
27 tan2 θ sec2 θ √ dx = dθ
= √ dθ 4 + x2 2 sec θ
9 + 9 tan2 θ = sec θdθ = ln | sec θ + tan θ| + c
= 9 tan2 θ sec θdθ √
x + 4 + x2
= ln +c
=9 (sec2 θ − 1) sec θdθ 2

=9 sec3 θdθ − 9 sec θdθ 37. Let u = x2 + 8, du = 2xdx
1
9 9 1 9 1/2
= sec θ tan θ − ln | sec θ + tan θ| + c x x2 + 8dx = u du
2 √ 2 0 2√ 8
9
9 9 + x2 x 1 27 − 16 2
= = u3/2 =
2 3 3 3 8 3
√
9 9 + x2 x 38. Let x = 3 tan θ, dx = 3 sec2 θ dθ
− ln + +c
2 3 3 I= x2 x2 + 9dx
√ √
x 9 + x2 9 x + 9 + x2
= − ln +c = 27 tan2 θ sec2 θ 9 tan2 θ + 9dx
2 2 3
√ √ = 81 tan2 θ sec3 θdx
34. Let x = 2 2 tan θ, dx = 2 2 sec2 θdθ
x3 8 + x2 dx = 81 (sec2 θ − 1) sec3 θdx


√ √
= 81 (sec5 θ − sec3 θ)dx 17 13 81 2 + 13
= − ln
4 8 3
To compute sec5 θ dθ, we use integration by
39. Let x = tan θ, dx = sec2 θdθ.
parts with u = sec3 θ and dv = sec2 θdθ. x3 tan3 θ
√ dx = sec2 θdθ
sec5 θ dθ 1 + x2 sec θ

= sec3 θ tan θ − 3 sec3 θ tan2 θdθ = tan2 θ (tan θ sec θ) dθ
Let t = sec θ, dt = tan θ sec θdθ.
= sec3 θ tan θ −3 sec3 θ(sec2 θ − 1)dθ
= sec2 θ − 1 tan θ sec θdθ
= sec3 θ tan θ − 3 (sec5 θ − sec3 θ)dθ t3
= t2 − 1 dt = −t +c
3
4 sec5 θdθ sec3 θ
= − sec θ + c
3
= sec3 θ tan θ + 3 sec3 θdθ sec5 θdθ
sec3 tan−1 x
1 3 = − sec tan−1 x + c.
= sec3 θ tan θ + sec3 θdθ 3
4 4
40. Let x = 2 tan θ, dθ = 2sec2 θ dθ.
3
To compute sec θdθ and sec θ dθ, see Ex- x+1
ercise 27. √ dx
4 + x2
Putting all this together gives: 2 tan θ + 1
= √ 2sec2 θdθ
I = 81 (sec5 θ − sec3 θ)dx 4 + 4tan2 θ
81 243 2 tan θ + 1
= sec3 θ tan θ + sec3 θdθ = 2sec2 θ dθ
4 4 2 sec θ

− 81 sec3 θdθ = (2 tan θ + 1) (sec θ) dθ

81 81 =2 sec θ tan θdθ + sec θdθ
= sec3 θ tan θ − sec3 θdθ
4 4
81 81 = 2 sec θ + ln |sec θ + tan θ| + c
= sec3 θ tan θ − sec θ tan θ x x
4 8 = 2 sec tan−1 + ln sec tan−1
81 2 2
− ln | sec θ + tan θ| + c x
8 + tan tan−1 +c
2
x
We don’t worry about the result being in terms = 2 sec tan−1
2
of x since this is a deﬁnite integral. Our lim- −1 x x
+ ln sec tan + + c.
its of integration are x = 0 and x = 2. In 2 2
terms of θ this means the limits of integration x
2 41. √ dx
correspond to θ = 0 and tan θ = . x 2 + 4x
3 1 2x + 4 − 4
2
= √ dx
2 x2 + 4x
x2 x2 + 9dx 1 2x + 4 1 4
0 = √ dx − √ dx
81 81 2 x2 + 4x 2 x2 + 4x
= sec3 θ tan θ − sec θ tan θ Let u = x2 + 4x, du = (2x + 4) dx.
4 8
x=2 1 du 1 4
81 = √ − √ dx
− ln | sec θ + tan θ| 2 u 2 x2 + 4x − 4 + 4
 8 x=0 1 4
√ 3 √ = u1/2 − dx
81 13 2 81 13 2 2 2
= − (x + 2) − 4
4 3 3 8 3 3
= (x2 + 4x)
√
81 13 2 − 2 log x2 + 4x +
2
(x + 2) − 4 + c.
− ln +
8 3 3
81 81 81 2 2
− (1)(0) − (1)(0) − ln |1 + 0| 42. √ dx = √ dx
4 8 8 x2 − 6x x2 − 6x + 9 − 9


2 2
= dx = dx
2 2
(x − 3) − 9 4 − (x − 2)
Let u = x − 3, du = dx. Let u = x − 2, du = dx.
2 2
= √ du = √ du
u2 − 9 4 − u2
Let u = 3 sec θ, du = 3 sec θ tan θdθ. Let u = 2 sin θ, du = 2 cos dθ.
2 2
= 3 sec θ tan θdθ = 2 cos θdθ
2 2
(3 sec θ) − 9 4 − (2 sin θ)
1 1
=2 √ sec θ tan θdθ =2 cos θdθ
2θ − 1
sec 1 − sin2 θ
1 1
=2 sec θ tan θdθ =2 cos θdθ = 2 dθ = 2θ + c
tan θ cos θ
=2 sec θdθ = 2 ln |sec θ + tan θ| + c u x−2
= 2sin−1 + c = 2sin−1 + c.
u 2 2
= 2 ln sec sec−1
3 45. Using u = tan x, gives
−1 u
+ tan sec +c tan x sec4 xdx
3
u −1 u
= 2 ln + tan sec +c
3 3 = tan x(1 + tan2 x) sec2 xdx
x−3
= 2 ln
3 = u(1 + u2 )du = (u + u3 )du
x−3
+ tan sec−1 + c. 1 2 1 4
3 = u + u +c
2 4
x 1 1
43. √ dx = tan2 x + tan4 x + c
10 + 2x + x2 2 4
x Using u = sec x, gives
= √ dx
9 + 1 + 2x + x2
x tan x sec4 xdx
= dx
2
(x + 1) + 9 = tan x sec x sec3 xdx
x+1−1 1 4 1
= dx = u3 du = u + c = sec4 x + c
2 4 4
(x + 1) + 9
x+1 1 46. Using u = tan x gives
= dx − dx
2
(x + 1) + 9
2
(x + 1) + 9 tan3 x sec4 xdx = u3 (u2 + 1)du
Let u = x + 1, du = dx. u6 u4
u 1 = + + c1
= √ du− √ du 6 4
u 2+9 u2+9
tan6 x tan4 x
= + + c2
1 2u 1 6 4
= √ du− √ du
2 u 2+9 u 2 + 32 Using u = sec x gives
Let t = u2 + 9, dt = 2udu. tan3 x sec4 xdx = (u2 − 1)u3 du
1 dt u6 u4 sec6 x sec4 x
= √ dt− log u + u2 + 32 + c = − = −
2 t 6 4 6 4
√
2 3 2
= t − log u + u2 + 32 + c (tan x + 1) (tan x + 1)2
= −
6 4
= u2 + 9 − log u + u2 + 9 + c tan6 x tan4 x 1
= + − + c1
=
2
(x + 1) + 9 6 4 12
6 4
tan x tan x
2 = + + c2
− log (x + 1) + (x + 1) + 9 + c. 6 4

2 2 47. (a) This is using integration by parts followed
44. √ dx = √ dx by substitution
4x − x2 4 − 4 + 4x − x2


u = secn−2 x, dv = sec2 xdx = − ln |csc x + cot x| + c.
du = (n − 2) secn−2 x tan xdx, v = tan x = ln |csc x − cot x| + c.
I= secn xdx = secn−2 x tan x csc3 xdx = csc x.csc2 xdx
− (n − 2) secn−2 (sec2 x − 1)dx u = csc x, dv = csc2 xdx
du = − csc x. cot x, v = − cot x
= secn−2 x tan x
csc3 xdx
− (n − 2) (secn x − secn−2 x)dx
= − csc x. cot x
= secn−2 x tan x − (n − 2)I
− (− cot x) (− csc x. cot x)dx
+ (n − 2) secn−2 xdx (n − 1)I
= − csc x cot x − csc x.cot2 x dx
n−2 n−2
= sec x tan x + (n − 2) sec xdx
sec n−2
x tan x n − 2 = − csc x cot x − csc x. csc2 x − 1 dx
n−2
I= + sec xdx
n−1 n−1
= − csc x cot x − csc3 x dx+ csc xdx
3
(b) sec xdx
2 csc3 xdx = − csc x cot x + csc xdx
1 1
= sec x tan x + sec xdx = − csc x cot x + ln |csc x − cot x| + c
2 2
1 1 csc3 xdx
= sec x tan x + ln | sec x + tan x| + c
2 2 1
4
= (− csc x cot x + ln |csc x − cot x|) + c
(c) sec xdx 2
1 2 1
= sec3 x tan x + sec2 xdx 50. dx
3 3 cos x − 1
1 2 cos x + 1
= sec3 x tan x + tan x + c = dx
3 3 (cos x − 1) (cos x + 1)
cos x + 1
(d) sec5 xdx =− dx
sin2 x
1 3 1 cos x 1
= sec3 x tan x + sec3 xdx =− + dx
4 4 sin x sin x sin x
1 3 =− csc x (cot x + csc x) dx
= sec3 x tan x + sec x tan x
4 8
3
+ ln | sec x + tan x| + c = − csc x cot x − csc2 xdx
8
48. Make the substitution x = a sin θ. = (− csc x cot x) dx + −csc2 x dx
4b a 4b a = csc x + cot x + c and,
a2 − x2 dx = a2 − x2 dx 1
a 0 a 0 dx
4b π/2 cos x + 1
= a cos θ a2 − a2 sin2 θdθ cos x − 1
a 0 = dx
π/2 (cos x − 1) (cos x + 1)
= 4b a cos2 θdθ cos x − 1
0 =− dx
π/2 sin2 x
1 1 1 cos x 1
= 4ab x + sin 2x = abπ =− − dx
2 4 0 sin x sin x sin x
csc x + cot x =− csc x (cot x − csc x) dx
49. csc xdx = csc x dx
csc x + cot x
(csc x) cot x + csc2 x = − csc x cot x + csc2 xdx
= dx
csc x + cot x
Let u = csc x + cot x, = (− csc x cot x) dx − −csc2 x dx
du = − (csc x) cot x − csc2 x. = csc x − cot x + c
1
=− du = − ln |u| + c 51. Using a CAS we get
u


(Ex 3.2) cos4 x sin3 xdx 6.4 Integration of
1 2 Rational Functions
= − sin x2 cos x5 − cos x5 + c
7 35 Using Partial
√
(Ex 3.3) sin x cos5 xdx Fractions
2 4 x−5 x−5
= sin x11/2 − sin x7/2 1. =
11 7 x2 − 1 (x + 1)(x − 1)
2 3/2 A B
+ sin x + c = +
3 x+1 x−1
(Ex 3.5) cos4 xdx x − 5 = A(x − 1) + B(x + 1)
x = −1 : −6 = −2A; A = 3
1 3 3
= cos x3 sin x + cos x sin x + x + c x = 1 : −4 = 2B; B = −2
4 8 8
x−5 3 2
(Ex 3.6) tan3 x sec3 xdx 2−1
= −
x x+1 x−1
sin x4 sin x4 x−5 3 2
= 1/5 + 1/15 dx = − dx
cos x5 cos x3 x 2−1 x+1 x−1
sin x4
− 1/15 − 1/15 sin x2 cos x = 3 ln | x + 1| − 2 ln | x − 1| + c
cos x
− 2/15 cos x + c 5x − 2 5x − 2
2. =
Obviously my CAS used diﬀerent tech- x 2−4 (x + 2)(x − 2)
niques. The answers given by the book A B
= +
are simpler. x+2 x−2

1 2 5x − 2 = A(x − 2) + B(x + 2)
52. (a) − sin2 x cos5 x − cos5 x x = −2 : −12 = −4A; A = 3
7 35
1 2 x = 2 : 8 = 4B; B = 2
= − (1 − cos2 x) cos5 x − cos5 x
7 35 5x − 2 3 2
1 1 = +
= cos7 x − cos5 x x2 − 4 x+2 x−2
7 5
The conclusion is c = 0 5x − 2 3 2
dx = + dx
2 1 x2 − 4 x+2 x−2
(b) − tan x − sec2 x tan x
15 15 = 3 ln | x + 2| + 2 ln | x − 2| + c
1
+ sec4 x tan x
5 6x 6x
2 1 3. =
= − tan x − (1 + tan2 x) tan x x2 − x − 2 (x − 2)(x + 1)
15 15 A B
1 = +
+ (1 + tan2 x)2 tan x x−2 x+1
5
1 1 6x = A(x + 1) + B(x − 2)
= tan3 x + tan5 x x = 2 : 12 = 3A; A = 4
3 5
The conclusion is c = 0 x = −1 : −6 = −3B; B = 2
6x 4 2
= +
x2 − x − 2 x−2 x+1
53. The average power 6x
2π/ω dx
1
= 2π RI 2 cos2 (ωt) dt x 2−x−2

ω 0
4 2
ωRI 2 2π/ω 1 = + dx
= [1 + cos(2ωt)] dt x−2 x+1
2π 0 2 = 4 ln | x − 2| + 2 ln | x + 1| + c
2π/ω
ωRI 2 1
= t+ sin(2ωt) 3x 3x
4π 2ω 0 4. =
2
ωRI 2π 1 4ωπ 1 x2− 3x − 4 (x + 1)(x − 4)
= + sin − 0 = RI 2 A B
4π ω 2ω ω 2 = +
x+1 x−4

6.4. INTEGRATION OF RATIONAL FUNCTIONS USING PARTIAL FRACTIONS 381

4 1
= ln | x| − ln |x + 2| − ln |x + 3| + c
3x = A(x − 4) + B(x + 1) 3 3
3 5x − 23 5x − 23
x = −1 : −3 = −5A; A = 7. =
5 6x2 − 11x − 7 (2x + 1)(3x − 7)
12
x = 3 : 12 = 5B; B = A B
5 = +
2x + 1 3x − 7
3x 3/5 12/5
= + 5x − 23 = A(3x − 7) + B(2x + 1)
x2 − 3x − 4 x+1 x−4
1 51 17
3x x=− :− = − A; A = 3
2 − 3x − 4
dx 2 2 2
x 7 34 17
3/5 12/5 x= :− = B; B = −2
= + dx 3 3 3
x+1 x−4 5x − 23 3 2
2 − 11x − 7
= −
3 12 6x 2x + 1 3x − 7
= ln | x + 1| + ln | x − 4| + c
5 5 5x − 23
dx
−x + 5 −x + 5 6x2 − 11x − 7
5. = 3 2
x3 − x2 − 2x x(x − 2)(x + 1) = − dx
A B C 2x + 1 3x − 7
= + +
x x−2 x+1 3 2
= ln | 2x + 1| − ln | 3x − 7| + c
− x + 5 = A(x − 2)(x + 1) + Bx(x + 1) 2 3
+ cx(x − 2) 3x + 5 3x + 5
5 8. =
x = 0 : 5 = −2A : A = − 5x2 − 4x − 1 (5x + 1)(x − 1)
2 A B
1 = +
x = 2 : 3 = 6B : B = 5x + 1 x − 1
2
x = −1 : 6 = 3C : C = 2 3x + 5 = A(x − 1) + B(5x + 1)
1 22 6 11
−x + 5 5/2 1/2 2 x=− : = − A; A = −
=− + + 5 5 5 3
x3−x 2 − 2x x x−2 x+1 4
−x + 5 x = 1 : 8 = 6B; B =
dx 3
x3 − x2 − 2x 3x + 5 11/3 4/3
5/2 1/2 2 2 − 4x − 1
=− +
= − + + dx 5x 5x + 1 x − 1
x x−2 x+1
3x + 5
5 1 dx
= − ln | x| + ln | x − 2| 5x2 − 4x − 1
2 2 11/3 4/3
+ 2 ln | x + 1| + c = − + dx
5x + 1 x − 1
3x + 8 3x + 8 11 4
6. = =− ln |5x + 1| + ln |x − 1| + c
x3 + 5x2 + 6x x(x + 2)(x + 3)) 15 3
A B C
= + + x−1 x−1
x x+2 x+3 9. 3 =
x + 4x2 + 4x x(x + 2)2
3x + 8 = A(x + 2)(x + 3) + Bx(x + 3) A B C
+ cx(x + 2) = + +
x x + 2 (x + 2)2
4
x = 0 : 8 = 6A; A = x − 1 = A(x + 2)2 + Bx(x + 2) + Cx
3 1
x = −2 : 2 = −2B; B = −1 x = 0 : −1 = 4A; A = −
1 4
x = −3 : −1 = 3C; C = − 3
3 x = −2 : −3 = −2C; C =
2
3x + 8 4/3 1 1/3 1
= − − x = 1 : 0 = 9A + 3B + C; B =
x3 + 5x2 + 6x x x+2 x+3 4
3x + 8 x−1
dx
x 3 + 5x2 + 6x x3 + 4x2 + 4x
4/3 1 1/3 1/4 1/4 3/2
= − − dx =− + +
x x+2 x+3 x x + 2 (x + 2)2


x−1
dx 1
x3 + 4x2 + 4x dx
1/4 1/4 3/2 x3 + 4x
= − + + dx 1 −x
x x + 2 (x + 2)2 = + dx
1 1 3 x x2 + 4
= − ln | x| + ln | x + 2| − +c 1
4 4 2(x + 2) = ln |x| − ln(x2 + 4) + c
2
4x − 5 4x − 5
10. 3 − 3x2
= 2 4x2 − 7x − 17
x x (x − 3) 13.
A B C 6x2 − 11x − 10
= + 2+ 2 1 x − 31
x x x−3 = +
3 3 (2x − 5)(3x + 2)
4x − 5 = Ax(x − 3) + B(x − 3) + Cx2
= (A + C)x2 + (−3A + B)x + (−3B) =
2 1
+
A
+
B
5 7 7 3 3 2x − 5 3x + 2
B = ;A = − ;C =
3 9 9 x − 31 = A(3x + 2) + B(2x − 5)
4x − 5 7/9 5/3 7/9 5 57 19
=− + 2 + x= :− = A, A = −3;
x3 − 3x2 x x x−3 2 2 2
4x − 5 2 95 19
dx x=− :− = − B, B = 5;
x3 − 3x2 3 3 3
4x2 − 7x − 17
7/9 5/3 7/9
= − + 2 + dx 6x2 − 11x − 10
x x x−3 2 1 −3 5
7/9 51 7 = + +
=− |x| − + ln |x − 3| + c 3 3 2x − 5 3x + 2
ln 3x 9 4x2 − 7x − 17
x+2 x+2 dx
11. = 6x2 − 11x − 10
x3 + x x(x2 + 1) 2 1 5/3
= − + dx
A Bx + C 3 2x − 5 3x + 2
= + 2 2 1 5
x x +1 = x − ln | 2x − 5| + ln | 3x + 2| + c
3 2 9
x + 2 = A(x2 + 1) + (Bx + C)x
x3 + x 2x
= Ax2 + A + Bx2 + Cx 14. 2−1
=x+
x (x + 1)(x − 1)
= (A + B)x2 + Cx + A A B
=x+ +
A = 2; C = 1; B = −2 x+1 x−1
2x = A(x − 1) + B(x + 1)
x+2 2 −2x + 1
3+x
= + 2 A=B=1
x x x +1
x+2 2 −2x + 1 x3 + x 1 1
dx = + 2 dx 2−1
=x+ +
x 3+x x x +1 x x+1 x−1
2 2x 1 x3 + x
= − + dx dx
x x2 + 1 x2 + 1 x2 − 1
= 2 ln | x| − ln(x2 + 1) + tan−1 x + c 1 1
= x+ + dx
x+1 x−1
1 1 x2
12. = = + ln |x + 1| + ln |x − 1| + c
x3 + 4x x(x2 + 4) 2
A Bx + C
= + 2 2x + 3 2x + 3
x x +4 15. =
2 x2 + 2x + 1 (x + 1)2
1 = A(x + 1) + (Bx + C)x A B
1 = (A + B)x2 + Cx + A = +
x + 1 (x + 1)2
2x + 3 = A(x + 1) + B
A = 1; B = −1; C = 0
1 1 −x x = −1 : B = 1; A = 2
= + 2
x3 + 4x x x +4


2x + 3 2 1 1 −x + 2
= + = + dx
x2
+ 2x + 1 x + 1 (x + 1)2 x x2 − 2x + 4
2x + 3 1 1 2x − 2 1
dx = − + dx
x2 + 2x + 1 x 2 x2 − 2x + 4 (x − 1)2 + 3
2 1
= + dx 1
x + 1 (x + 1)2 = ln |x| − ln(x2 − 2x + 4)
1 2
= 2 ln | x + 1| − +c
x+1 1 x−1
+ √ tan−1 √ +c
2x 2x 3 3
16. 2 =
x − 6x + 9 (x − 3)2 3x3 + 1
A B 19.
= + x3 − x2 + x − 1
x − 3 (x − 3)2 3x2 − 3x + 4
=3+ 3
2x = A(x − 3) + B x − x2 + x − 1
A = 2; B = 6 3x2 − 3x + 4
=3+ 2
(x + 1)(x − 1)
2x 2 6 Ax + B C
= + =3+ 2 +
x2 − 6x + 9 x − 3 (x − 3)2 x +1 x−1
2x
dx 3x2 − 3x + 4 = (Ax + B)(x − 1) + C(x2 + 1)
x2 − 6x + 9
= Ax2 − Ax + Bx − B + Cx2 + C
2 6
= + dx x = 1 : 4 = 2C; C = 2
x − 3 (x − 3)2 A+c=3:A=1
6
= 2 ln |x − 3| − +c − A + B = −3 : B = −2
x−3
x3 − 4 −2x2 − 2x − 4 3x3 + 1 x−2 2
17. =1+ =3+ 2 +
x3 + 2x2 + 2x x(x2 + 2x + 2) x3− x2 + x − 1 x +1 x−1
A Bx + c 3x3 + 1
=1+ + 2 dx
x x + 2x + 2 x 3 − x2 + x − 1

− 2x2 − 2x − 4 = A(x2 + 2x + 2) + (Bx + c)x x−2 2
= 3+ 2 + dx
= (A + B)x2 + (2A + c)x + 2A x +1 x−1
A = −2; B = 0; C = 2 x 2 2
= 3+ 2 − + dx
x + 1 x2 + 1 x − 1
x3 − 4 1
x3 + 2x2 + 2x = 3x + ln(x2 + 1) − 2 tan−1 x
−2 2 2
=1+ + 2 + 2 ln | x − 1| + c
x x + 2x + 2
x3 − 4 2x4 + 9x2 + x − 4 x2 + x − 4
dx 20. = 2x +
x3 + 2x2 + 2x x3 + 4x x(x2 + 4)
−2 2 A Bx + C
= 1+ + dx = 2x + + 2
x (x + 1)2 + 1 x x +4
= x − 2 ln |x| + 2 tan−1 (x + 1) + c x2 + x − 4 = A(x2 + 4) + (Bx + C)x
4 4 = (A + B)x2 + Cx + 4A
18. = A = −1; B = 2; C = 1
x3 − 2x2 + 4x x(x2 − 2x + 4)
A Bx + C 2x4 + 9x2 + x − 4 1 2x + 1
= + 2 = 2x − + 2
x x − 2x + 4 x 3 + 4x x x +4
4 = A(x2 − 2x + 4) + (Bx + C)x 1 2x 1
= 2x − + 2 + 2
= (A + B)x2 + (−2A + C)x + 4A x x +4 x +4
A = 1; B = −1; C = 2 2x + 9x2 + x − 4
4
dx
x3 + 4x
4 1 −x + 2 1 2x 1
= + 2 = 2x − + 2 + dx
x3 − 2x 2 + 4x x x − 2x + 4 x x + 4 x2 + 4
4 1 x
dx = x2 − ln |x| + ln(x2 + 4) + tan−1 + c
x3 − 2x2 + 4x 2 2


x3 + x + 2 11 2 26. Let u = x2 , du = (2x) dx.
21. =x−2+ +
x2 + 2x − 8 x+4 x−2 x 1 2x
dx = dx
x3 + x + 2 x4 + 1 2 x4 + 1
dx 1 du 1
x2 + 2x − 8 = 2+1
= tan (u) + c
11 2 2 u 2
= x−2+ + dx 1 2
x+4 x−2 = tan x + c.
2
x2
= − 2x + 11 ln | x + 4|
2 4x − 2 −4x + 1 1
+ 2 ln | x − 2| + c 27. = +
16x4 − 1 4x2 + 1 2x + 1
x2 + 1 2/7 37/7 4x − 2
22. =− + dx
x 2 − 5x − 6 x+1 x−6 16x4 − 1
−4x + 1 1
x2 + 1 = 2+1
+ dx
dx 4x 2x + 1
x2 − 5x − 6
2/7 37/7 1 8x 1 1
= − + dx = − + + dx
x+1 x−6 2 4x2 + 1 4x2 + 1 2x + 1
1 1
2 37 = − ln |4x2 + 1| + tan−1 (2x)
= − ln | x + 1| + ln |x − 6| + c 2 2
7 7
1
+ ln |2x + 1| + c
x+4 2 1 3 2
23. = + −
x3+ 3x 2 + 2x x x+2 x+1
3x + 7 13/32 1/32 3x/8 + 7/8
x+4 28. = − −
dx x4 − 16 x−2 x+2 x2 + 4
x3 + 3x2 + 2x
2 1 3 3x + 7
= + − dx dx
x x+2 x+1 x4 − 16
13/32 1/32 3x/8 + 7/8
= 2 ln | x| + ln | x + 2| − 3 ln | x + 1| + c = − − dx
x−2 x+2 x2 + 4
1 1/3 (x + 2)/3 13/32 1/32 3 2x
24. = − = − −
x3 − 1 (x − 1) (x2 + x + 1) x−2 x+2 16 x2 + 4
1
dx 7 1
x3 − 1 − dx
1 1 x+2 8 x2 + 4
= − dx 13 1
3 (x − 1) (x2 + x + 1) = ln |x − 2| − ln |x + 2|
32 32
1 1 1 2x + 4 3 7 x
= − dx − ln(x2 + 4) − tan−1 + c
3 (x − 1) 2 (x2 + x + 1) 16 16 2
1 1 1 2x + 1
= − x3 + x
3 (x − 1) 2 (x2 + x + 1) 29.
1 3 3x2 + 2x + 1
− dx
2 (x2 + x + 1) x 2 1 10x + 2
1 1 1 2x + 1 = − +
= − 3 9 9 3x2 + 2x + 1
3 (x − 1) 2 (x2 + x + 1) x3 + x
dx
1 3 3x2 + 2x + 1
− dx
2 (x + 1/2)2 + 3/4 x 2 1 10x + 2
1 1 = − + dx
= ln |x − 1| − ln x2 + x + 1 3 9 9 3x2 + 2x + 1
3 2 x 2 15 6x + 2
√ 2x + 1 = − + 2 + 2x + 1
− 3tan −1
√ +c 3 9 9 3 3x
3 14 1
− dx
9 3 3(x + 1/3)2 + 2/3
25. Let u = x4 − x, du = 4x3 − 1 dx. x2 2 5
4x3 − 1 du = − x+ ln(3x2 + 2x + 1)
dx = 6 √9 27
x 4−x u 2 2 3x + 1
= ln |u| + c = ln x4 − x + c. − tan−1 √ +c
27 2


x3 − 2x = −x2 cos x + 2 {x sin x + cos x} + c.
30.
2x2 − 3x + 2
x 4 1 21x − 6 34. Let u = x, dv = e2x dx .
= + +
2 3 4 2x2 − 3x + 2 e2x
so that du = dx and v = .
x3 − 2x 2
dx e2x e2x
2x2 − 3x + 2 xe2x dx = x − dx
x 4 1 21x − 6 2 2
= + + dx e2x e2x
2 3 4 2x2 − 3x + 2 =x − +c
x 4 21 4x − 3 2 4
= + + 2 − 3x + 2
2 3 16 2x
39 1 35. Let u = sin2 x − 4 ,
+ dx
32 (x − 3/4)2 + 7/16 so that du = 2 sin x cos x dx.
x2 4 21 sin x cos x 1 du
= + x+ ln(2x2 − 3x + 2) dx =
4 √ 3 16 sin2 x − 4 2 u
39 7 4x − 3 1 1
− tan−1 √ +c = ln |u| + c = ln sin2 x − 4 + c
56 7 2 2
4x2 + 3 3 x−3 36. Let t = ex , dt = ex dx and e3x = t3
31. = + 2 2ex 2
x3 + x2 + x x x +x+1 dx = dt.
e 3x + ex t3 + t
4x2 + 3
dx 2 2t
x 3 + x2 + x = − 2 dt = 2 ln |t| − ln t2 + 1 + c
3 x−3 t t +1
= + dx = 2 ln |ex | − ln e2x + 1 + c
x x2 + x + 1
3 x + 1/2 7/2
= + − dx 4x2 + 2 Ax + B Cx + D
x x2 + x + 1 x2 + x + 1 37. = 2 + 2
1 (x2 + 1)2 x +1 (x + 1)2
= 3 ln | x| + ln | x2 + x + 1|
2 4x2 + 2 = (Ax + B)(x2 + 1) + (Cx + D)
7 −1 2x + 1 = Ax3 + Bx2 + (A + C)x + (B + D)
− √ tan √ +c
3 3 A = 0; B = 4; C = 0; D = −2
4x + 4 1 2 −x − 3
32. = + 2+ 2 4x2 + 2 4 −2
x4 +x 3 + 2x2 x x x +x+2 = 2 +
(x2 + 1)2 x + 1 (x2 + 1)2
4x + 4
dx
x4 + x3 + 2x2 x3 + 2 Ax + B Cx + D
1 2 −x − 3 38. = 2 + 2
= + + 2 dx (x2 + 1)2 x +1 (x + 1)2
x x2 x +x+2
2 1 x3 + 2 = (Ax + B)(x2 + 1) + cx + D
= ln |x| − − ln(x2 + x + 2) = Ax3 + Bx2 + (A + c)x + (B + D)
x 2
5 2x + 1 A = 1; B = 0; C = −1; D = 2
− √ tan−1 √ +c
7 7
x3 + 2 x −x + 2
2
33. Let u = x , dv = (sin x) dx = 2 +
(x2 + 1)2 x + 1 (x2 + 1)2
So that du = (2x) dx and v = − cos x.
4x2 + 3
x2 sin xdx 39.
(x2 + x + 1)2
Ax + B Cx + D
= x2 (− cos x) − (− cos x) (2x) dx = 2 +
x + x + 1 (x2 + x + 1)2
= −x2 cos x + 2 x (cos x) dx 4x2 + 3 = (Ax + B)(x2 + x + 1) + cx + D
= Ax3 + Ax2 + Ax + Bx2 + Bx + B + cx + D
Let u = x, dv = cos xdx,
A=0
so that du = dx and v = sin x.
A+B =4:B =4
x2 sin xdx A + B + c = 0 : C = −4
B + D = 3 : D = −1
= −x2 cos x + 2 x cos xdx


4x2 + 3 To see that the two answers are equivalent,
(x2+ x + 1)2 note that
4 4x + 1 x2 x2 + 1 1
= 2 − 2 ln 2 = − ln 2
= − ln 1 + 2
x + x + 1 (x + x + 1)2 x +1 x x
x4 + x3 x3 − 8x2 − 8 43. (a) Partial fractions
40. 2 + 4)2
=1+
(x (x2 + 4)2
Ax + B Cx + D (b) Substitution method
=1+ 2 + 2
x +4 (x + 4)2 (c) Substitution and Partial fractions.
x3 − 8x2 − 8 = (Ax + B)(x2 + 4) + cx + D (d) Substitution
= Ax3 + Bx2 + (4A + c)x + (4B + D)
A = 1; B = −8; C = −4; D = 24 44. (a) Partial fractions
4 3
x +x x−8 −4x + 24 (b) Substitution and Partial fractions.
2 + 4)2
=1+ 2 + 2
(x x +4 (x + 4)2
(c) Partial fractions
3 2
41. Let u = x + 1, du = 3x dx (d) Partial fractions
3 3x2
dx = dx
x4 + x x3 (x3 + 1) cos x
1 45. sec3 xdx = 2 dx
= du 1 − sin2 x
(u − 1)u
Let u = sin x, so that du = cos xdx.
1 1 cos x dx du
= − du 2 = 2
u−1 u 2
1 − sin x (1 − u2 )
= ln |u − 1| − ln |u| + c 1
= 2 2 du
u−1 (1 − u) (1 + u)
= ln +c
u By partial fractions,
x3 1 1 1 1
= ln +c 2 2 = 4 +
(1 − u) (1 − u)2
x3
+1 (1 − u) (1 + u)
On the other hand, we can let 1 1
1 1 + +
u = , du = − 2 dx (1 + u) (1 + u)2
x x
3 3u2 Hence, sec3 xdx
dx = − du
x 4+x 1 + u3 1 1
= − ln |1 − u| + + ln |1 + u|
= − ln |1 + u3 | + c = − ln |1 + 1/x3 | + c 4 (1 − u)
To see that the two answers are equivalent, 1
− +c
note that (1 + u)
x3 x3 + 1 1 1
ln 3 = − ln = − ln |1 + 1/x3 | = − ln |1 − sin x| +
x +1 x3 4 (1 − sin x)
1
42. Let u = x2 + 1, du = 2xdx + ln |1 + sin x| − +c
(1 + sin x)
2 2x
dx = dx
x3 + x x2 (x2 + 1)
du u−1 6.5 Integration Table
= = ln +c
u(u − 1) u and Computer
x2
= ln 2
x +1
+c Algebra Systems
1 1 x
Let u = , du = − 2 dx 1. dx
x x (2 + 4x)2
2 2u 2 1
dx = − du = + ln | 2 + 4x| + c
x3 + x 1 + u2 16(2 + 4x) 16
1 1 1
= − ln |1 + u2 | + c = − ln 1 + 2 + c = + ln | 2 + 4x| + c
x 8(2 + 4x) 16

6.5. INTEGRATION TABLE AND COMPUTER ALGEBRA SYSTEMS 387

x2 1 3 2 t3
2. dx = t 2t6 − 4 4 − t6 + sin−1 + c
(2 + 4x)2 24 3 2
1 4 1
√
= 2 + 4x − − 4 ln |2 + 4x| + c π 3
64 2 + 4x t8 4 − t6 dt = −
0 9 12
3. Substitute u = 1 + ex
√ √ 8. Substitute u = et √
e2x 1 + ex dx = (u − 1) u du 16 − u2
16 − e2t dt = du
u
= (u3/2 − u1/2 ) du √
4 + 16 − u2
2 5/2 2 3/2 = 16 − u2 − 4 ln +c
= u − u +c u
5 3 √
2 2 2t − 4 ln
4 + 16 − e2t
= (1 + ex )5/2 − (1 + ex )3/2 + c = 16 − e +c
5 3 et
ln 4 √ √
4. Substitute u = ex 16 − e2t dt = − 15 + 4 ln 15 + 4
0
e3x 1 + e2x dx = u2 1 + u2 du
1 9. Substitute u = ex
= u(1 + 2u2 ) 1 + u2 ex 1
8 √ dx = √ du
1 e 2x + 4 u 2+4
− ln |u + 1 + u2 | + c
8 = ln(u + 4 + u2 ) + c
1
= ex (1 + 2e2x ) 1 + e2x = ln(ex + 4 + e2x ) + c
8 ln 2
√
1 ex 2 2+2
− ln |ex + 1 + e2x | + c √ dx = ln √
8 0 e2x + 4 1+ 5
5. Substitute u = 2x
10. Substitute u = x2
√ √
2
x 2 x x4 − 9 1 4 u2 − 9
√ dx √ dx = du
1 + 4x2 3 x2 2 3 u
4
1 u2 1 |u|
= √ du = u2 − 9 − 3 sec−1
8 1 + u2 2 3
1 u √ 3
= − 1 + u2 7 3 −1 4
8 2 = − sec
1 2 2 3
− ln(u + 1 + u2 ) + c
2 11. Substitute u = x − 3
1 √
= x 1 + 4x2 6x − x2
8 dx
1 (x − 3)2
− ln(2x + 1 + 4x2 ) + c (u + 3)(6 − (u + 3))
16 = du
√ u2
6. Substitute u = sin x
cos x 9 − u2
dx = du
2
sin x(3 + 2 sin x) u2
1 1 u
= du =− 9 − u2 − sin−1 + c
u 2 (3 + 2u) u 3
1
2 3 + 2u 1 =− 9 − (x − 3)2
= ln − +c x−3
9 u 2u x−3
2 3 + 2 sin x 1 − sin−1 +c
= − +c 3
9 sin x 3 sin x
12. Substitute u = tan x
7. Substitute u = t3 sec2 x
√ dx
t8 4 − t6 dt tan x 8 tan x − tan2 x
1 1
= u2 4 − u2 du = √ du
3 u 8u − u2
√
1 u 16 u 8u − u2
= 2u2 − 4 4 − u2 + sin−1 +c =− +c
3 8 8 2 4u

√
8 tan x − tan2 x u
=− +c = −2 √ du
4 tan x 1+u
2 √
13. tan6 udu = −2 (u − 2) 1 + u + c
3
1 4 √
= tan5 u − tan4 udu = − (cos x − 2) 1 + cos x + c
5 3
1 1 20. Substitute u = x2
√
= tan5 u − tan3 u − tan2 udu √
5 3 x 1 + 4x2 1 1 + 4u
dx = du
1 1 x4 2 u2
= tan5 u − tan3 u + tan u − u + c. √ √
5 3 1 + 4u 1 + 4u − 1
=− + ln √ +c
2u 1 + 4u + 1
14. csc4 udu √ √
1 + 4x2 1 + 4x2 − 1
1 2 =− + ln √ +c
= − csc2 u cot u + csc2 udu 2x 2
1 + 4x2 + 1
3 3
1 2 21. Substitute u = sin t
= − csc2 u cot u − cot u + c. sin2 t cos t
3 3 dt
15. Substitute u = sin x sin2 t + 4
cos x 1 u2
√ dx = √ du = √ du
sin x 4 + sin x u 4+u u2 + 4
√ u 4
1 4+u−2 = 4 + u2 − ln(u + 4 + u2 ) + c
= √ ln √ +c 2 2
4 4+u+2 1
√ = sin t 4 + sin2 t
1 4 + sin x − 2 2
= ln √ +c
2 4 + sin x + 2 − 2 ln sin t + 4 + sin2 t + c
√
16. Substitute u = x2 22. Substitute u = t
x5 1 u2 √
√ dx = √ du ln t
4+x 2 2 4 + u2 √ dt = 2 ln u du
t √ √ √
1 2 √ = 2u ln u − 2u + c = 2 t ln t − 2 t + c
= (3u2 − 16u + 128) 4 + u + c
2 15 2
23. Substitute u = −
1 x2
= (3x4 − 16x2 + 128) 4 + x2 + c 2
15 e−2/x 1
dx = eu du
17. Substitute u = x2 x3 4
1 1 1 2

x3 cos x2 dx = u cos u du = eu + c = e−2/x + c
2 4 4
1 24. Substitute u = 2x2
= (cos u + u sin u) + c 1
2 2
x3 e2x dx = ueu du
1 1 8
= cos x2 + x2 sin x2 + c 1 1 2
2 2 = (u − 1)eu + c = (2x2 − 1)e2x + c
8 8
18. Substitute u = x2 x
x sin(3x2 ) cos(4x2 ) dx 25. √ dx
4x − x2
1 2−x
= sin(3u) cos(4u) du = − 4x − x2 + 2 cos−1 +c
2 2
1 cos u cos 7u
= − +c 26. e5x cos 3x dx
2 2 14
cos x2 cos 7x2 1
= − +c = (5 cos 3x + 3 sin 3x)e5x + c
4 28 34
19. Substitute u = cos x 27. Substitute u = ex
sin 2x 2 sin x cos x
√ dx = √ dx ex tan−1 (ex )dx = tan−1 u du
1 + cos x 1 + cos x

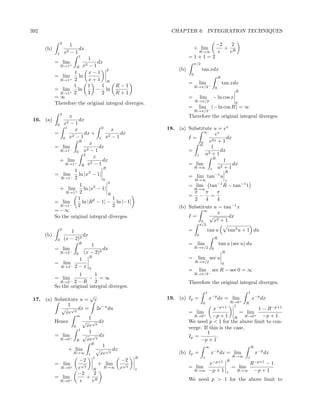
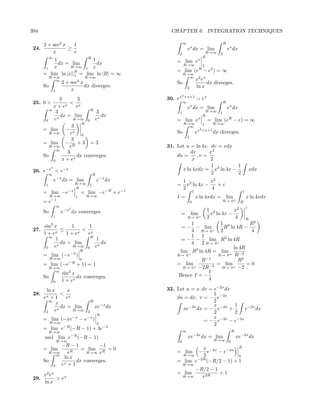
6.6. IMPROPER INTEGRALS 389

1 1 1
= u tan−1 u − ln(1 + u2 ) + c (b) x−4/3 dx = lim+ x−4/3 dx
2 0 R→0 R
1
= ex tan−1 ex − ln(1 + e2x ) + c 1
2 = lim (−3x−1/3 )
R→0+ R
28. Substitute u = 4x −1/3
1 = lim+ (−3)(1 − R )=∞
(ln 4x)3 dx = (ln u)3 dx R→0
4 So the original integral diverges.
1
= u(ln u)3 − 3 (ln u)2 dx ∞ R
4 4. (a) x−4/5 dx = lim x−4/5 dx
1 R→∞
= u(ln u)3 1
R
1
4 = lim 5x1/5
3
− u(ln u)2 − 2u ln u + 2u + c R→∞ 1
4 = lim 5R1/5 − 5 = ∞
= x(ln 4x)3 − 3x(ln u)2 + 6x ln 4x − 6x + c R→∞
So the original integral diverges.
29. Answer depends on CAS used. ∞ R
(b) x−6/5 dx = lim dx
30. Answer depends on CAS used. 1 R→∞ 1
R
−1/5
= lim −5x
31. Any answer is wrong because the integrand is R→∞ 1
undefined for all x = 1. = lim −5R−1/5 + 5 = 5
R→∞
32. Answer depends on CAS used. 1 R
1 1
5. (a) √
dx = lim− √ dx
33. Answer depends on CAS used. 0 1−x R→1 0 1−x
√ R
34. Answer depends on CAS used. = lim − 2 1 − x 0
R→1−
√
35. Answer depends on CAS used. = lim −2( 1 − R − 1) = 2
R→1−
bπ 5
2 R
2
36. Maple gives the result: (b) √dx = lim− √ dx
1 1 5−x R→5 1 5−x
a2 √ R
= lim− − 4 5 − x 1
R→5
37. If the CAS is unable to compute an antideriva- √
tive, f (x) dx is generally printed showing this = lim− −4( 5 − R − 2) = −8
R→5
inability.
1 R
2 2
6. (a) √ dx = lim− √ dx
1 − x2 R→1 1 − x2
6.6 Improper Integrals 0
R
0

= lim− 2 sin−1 x
1. (a) improper, function not defined at x = 0 R→1 0

(b) not improper, function continuous on = lim− 2(sin−1 R − sin−1 0)
R→1
entire interval π
=2 −0 =π
2
(c) not improper, function continuous on
1/2
on entire interval 2
(b) √ dx
0 x 1 − x2
2. (a) improper, interval is infinite 1/2
2
= lim+ dx √
(b) improper, function not defined at x = 0 R→0 R x 1 − x2
√ 1/2
(c) improper, interval is infinite 1 + 1 − x2
= lim −2 ln =∞
1 1 R→0+ x
R
3. (a) x−1/3 dx = lim+ x−1/3 dx Therefore the original integral diverges.
0 R→0 R
1
3 2/3 ∞ R
= lim+ x
R→0 2 R
7. (a) xex dx = lim xex dx
0 R→∞ 0
3 3 R
= lim+ 1 − R2/3 = = lim (xex − ex )
R→0 2 2 R→∞ 0


= lim eR (R − 1) + 1 = ∞ 1
R→∞ Hence, I = −
16
−1 −1
(b) Substitute u = −2x 1 1
∞ −∞ 9. (a) 2
dx = lim dx
1 −∞ x R→−∞ R x2
I= x2 e−2x dx = − u2 eu du −1
1 8 −2 1
= lim −
1 −2 2 u R→−∞ x R
= u e du 1
8 −∞ = 1 + lim =1
−2 R→−∞ R
1
= lim u2 eu du 0
1 R
1
8 R→−∞ R dx = lim+ dx
−2 x 2 R→0 x2
1 −1 −1
= lim (u2 eu − 2ueu + 2eu ) 1
R
8 R→−∞ R = lim+ −
10 −2 1 R 2 R→0 x −1
= e + lim e (−R + 2R − 2)
8 8 R→−∞ 1
= −1 − lim =∞
But, lim e (−R2 + 2R − 2)
R
R→0+ R
R→−∞ So the original integral diverges.
= lim e−R (−R2 − 2R − 2) −1 −1
R→∞ 1 1
−R2 − 2R − 2 (b) √ dx = lim √ dx
= lim −∞
3
x R→−∞ R 3
x
R→∞ eR −1
−2R − 2 −2 3 2/3
= lim = lim R = 0 = lim x
R→∞ e R R→∞ e R→−∞ 2
R
5 3 3
Hence, I = e−2 = + lim R2/3 = ∞
4 2 2 R→−∞
8. (a) Substitute u = 3x
1 ∞ R
I = lim x2 e3x dx 10. (a) cos xdx = lim cos xdx
−∞→1 −∞ R→∞
0 0
3 R
1
= u2 eu du = lim sin x
27 −∞ R→∞ 0
1
3 = lim (sin R − sin 0)
R→∞
= lim (u2 eu − 2ueu + 2eu )
27 R→−∞ R
5 3 1 ∞
= e − lim eR (R2 − 2R + 2) (b) cos xe− sin x dx
27 27 R→−∞
0
But, lim eR (R2 − 2R + 2) R
R→∞
−R 2 = lim cos xe− sin x dx
= lim e (R + 2R + 2) R→∞ 0
R→∞ R
R2 + 2R + 2 = lim −e− sin x
= lim =0 R→∞ 0
R→∞ eR
5 3 = lim −e− sin R + 1
Hence, I = e R→∞
27 So the original integral diverges.
(b) Substitute u = −4x
0 1
I= xe−4x dx 11. (a) ln xdx
−∞ 0
0 1
1
= ueu du = lim+ ln xdx
16 −∞ R→0 R
0 1
1
= lim ueu du = lim (x ln x − x)
16 R→−∞ R R→0+ R
1
0 = lim (−1 − R ln R + R)
= lim (ueu − eu ) R→0+
16 R→−∞ R
ln R
1 1 = −1 − lim+
R R→0 1/R
=− + lim e (R − 1)
16 16 R→−∞ 1/R
R
But, lim e (R − 1) = −1 − lim+
R→0 −1/R2
R→−∞
= lim e−R (−R − 1) = 0 = −1 + lim+ R = −1
R→∞ R→0


π/2 R
2x
(b) sec2 xdx = lim− dx
0 R→1 −4 x2 − 1
R R
= lim 2
sec xdx = lim− ln(x2 − 1) −4
R→1
R→π/2− 0
R = lim− ln(R2 − 1) − ln 15 = ∞
R→1
= lim tan x So the original integral diverges.
R→π/2− 0
= lim tan R − tan 0 = ∞ π
R→π/2−
Therefore the original integral diverges. 14. (a) xsec2 xdx
0
π/2 π/2 π
12. (a) cot xdx = xsec2 xdx + xsec2 xdx
0 0 π/2
π/2 R
cos x = lim (x tan x + ln |cos x|)|0
= lim+ dx R→π/2−
R→0 R sin x + lim (x tan x + ln |cos x|)|R
π
π/2 R→π/2+
= lim+ ln | sin x| =∞
R→0 R
= ln | sin(π/2)| − lim+ ln | sin R| = ∞ So the original integral diverges.
R→0
2
So the original integral diverges. 2
π/2 (b) dx
0 x3 − 1
(b) tan xdx 1
2 2
2
0 = dx + dx
R 3−1 3−1
sin x 0 x 1 x
= lim dx R
2
R→π/2 0 cos x = lim dx
R R→1− 0 x3 − 1
= lim − ln | cos x| 2
2
R→π/2 0 + lim dx
3−1
= lim (− ln | cos R| + ln 1) = ∞ R x
R→1 +

R→π/2
ln x2 + x + 1
So the original integral diverges. = lim− 2 −
R→1 6
3
2 R
13. (a) dx tan−1 2x+1√
0 x2 − 1 3 ln (x − 1) 
3 − √ +
1 1 3 3
= − + dx 0
0 x+1 x−1
R
1 1 ln x2 + x + 1
= lim− − + dx + lim+ 2 −
R→1 x+1 x−1 R→1 6
0
3 R
1 1 tan−1 2x+1
√
+ lim+ − + dx 3 ln (x − 1) 
R→1 R x+1 x−1 − √ +
Both of these integrals behave like 3 3
1 0
1 =∞
lim+ dx
R→0 R x ∞
= lim+ (ln 1 − ln R) 1
R→0 15. (a) 2
dx
1 −∞ 1 + x
= lim ln =∞ 0 ∞
R 1 1
R→0+ = dx + ds dx
So the original integral diverges. −∞ 1 + x2 0 1 + x2
0
4
2x 1
(b) dx = lim dx
2−1 R→−∞ R 1 + x2
1 x R
4
2x 1
= lim+ dx + lim dx
R→1 x2 − 1 R→∞ 0 1 + x2
R
= lim ln(x2 − 1) R
4 = lim tan x|R + lim tan−1 x|R
−1 0
0
R→∞ R→∞
R→1+
= lim (tan−1 0 − tan−1 R)
= lim+ ln 15 − ln(R2 − 1) = ∞ R→−∞
R→1 + lim (tan−1 R − tan−1 0)
1 R→∞
2x π π
dx =0− − + −0=π
−4 x2 − 1 2 2


2 −2 2
1
(b) dx + lim + R
1 x2 − 1 R→∞ e e
1 1 =1+1=2
= lim+ 2−1
dx π/2
R→1 R x
2 (b) tan xdx
1 x−1 0
= lim ln R
R→1+ 2 x+1 R
= lim tan xdx
1 1 1 R−1 R→π/2− 0
= lim ln − ln R
R→1 + 2 3 2 R+1
=∞ = lim − ln cos x
R→π/2−
Therefore the original integral diverges. 0
= lim − (− ln cos R) = ∞
R→π/2
2
x Therefore the original integral diverges.
16. (a) dx
0 x2 − 1
1
x 2
x 18. (a) Substitute u = ex
= dx + dx ∞
2−1 2−1 ex
0 x 1 x I= dx
R
x 0 e2x + 1
∞
= lim− dx 1
R→1 0 x2 − 1 = 2+1
dx
2 1 u
x R
+ lim+ 2−1
dx 1
R→1 R x = lim dx
R R→∞ 1 u2 + 1
1 R
= lim− ln |x2 − 1| = lim tan−1 u
R→1 2 0 R→∞ 1
2
1 2 = lim tan−1 R − tan−1 1
+ lim+ ln |x − 1| R→∞
R→1 2 R π π π
= − =
1 2 1 2 4 4
= lim− ln |R − 1| − ln |−1|
R→1 2 2 (b) Substitute u = tan−1 x
= −∞ ∞
x
So the original integral diverges. I= √ dx
x 2+1
0
π/2
2
1 = tan u tan2 u + 1 du
(b) dx 0
0 (x − 2)2 R
R
1 = lim tan u (sec u) du
= lim− dx R→π/2 0
R→2 0 (x − 2)2 R
R = lim sec u
1 R→π/2
= lim− 0
R→2 2 − x 0
= lim −
sec R − sec 0 = ∞
1 1 R→π/2
= lim − =∞
2−R 2
R→2− Therefore the original integral diverges.
1 1
√ 19. (a) Ip = x−p dx = lim x−p dx
17. (a) Substitute u = x R→0+
0 R
1 1
√ √x dx = 2e−u du x −p+1
1 − R−p+1
xe = lim+ = lim+
∞
1 R→0 −p + 1 R R→0 −p + 1
Hence √ √x dx We need p < 1 for the above limit to con-
0 xe verge. If this is the case,
1
1 1
= lim+ √ √x dx Ip = .
R→0 R xe −p + 1
R
1 ∞ R
+ lim √ √x dx
R→∞ 1 xe (b) Ip = x−p dx = lim x−p dx
1 R 1 R→∞ 1
−2 −2 R
= lim+ √ + lim √ x−p+1 R−p+1 − 1
R→0 e x
R
R→∞ e x
1
= lim = lim
R→∞ −p + 1 1
R→∞ −p + 1
−2 2
= lim+ + R We need p > 1 for the above limit to
R→0 e e


converge.
(b) Case1: If r > 0
(c) There are three cases. Substitute u = rx
0
Case 1: p > −1
∞ R I= xerx dx
xp dx = lim xp dx 0
−∞
0 R→∞ 0 1
p+1 R = lim ueu du
x Rp+1 r2 R→−∞ R
= lim = lim =∞ 1
R→∞ p+1 0
R→∞ p + 1
= 2 lim (ueu − eu )|R
0
∞
r R→−∞
So xp dx diverges. 1 1
−∞ = 2 − 2 lim eR (R − 1)
Case 2: p = −1 r r R→−∞
∞
1 1 1
We have already seen that dx = 2 −0= 2
x r r
−∞ 0
diverges.
So xerx dx converges for r > 0.
Case 3: p < −1 −∞
1 1
p p
x dx = lim x dx Case2: For r ≤ 0,
0 R→0+ R 0
p+1 1 the integral xerx dx diverges.
x
= lim+ −∞
R→0 p + 1 R Therefore, for all r < 0
1 − Rp+1 ∞
the integral 0 xerx dx converges.
= lim+ =∞
R→0 p+1
∞
x x 1
So xp dx diverges. 21. 0 < < 3 = 2
−∞ 1 + x3 x x
∞ R
20. (a) Case1: If r ≥ 0 1 1
2
dx = lim dx
Substitute u = rx. 1 x R→∞ 1 x2
∞
R
I= xerx dx = lim −
1
0 R→∞ x 1
R
1 1
= lim
2 R→∞
ueu du = lim − + 1 = 1
r 0 R→∞ R
1 R ∞
= 2 lim (ueu − eu )|0 x
r R→∞ So dx converges.
1 1 1 1 + x3
= 2 lim eR (R − 1) − 2 = ∞
r R→∞ r
x2 − 2 3x2
∞
rx 22. ≤ 4 = 3x−2
So xe dx diverges for r ≥ 0. x4 + 3 x
0 ∞ R

Case2: For r < 0, 3x−2 dx = lim 3x−2 dx
1 R→∞ 1
Substitute u = −rx
∞ −3
R
−3
I= xerx dx = lim = lim +3=3
R→∞ x 1
R→∞ R
0
−R ∞ 2
1 x −2
= 2 lim ueu du So dx converges.
r R→∞ 0 1 x4 + 3
0
1
= − 2 lim ueu du x x 1
r R→∞ −R 23. > 3/2 = 1/2 > 0
1 0 x3/2 −1 x x
= − 2 lim (ueu − eu )|−R ∞ R
r R→∞
1 1 x−1/2 dx = lim x−1/2 dx
= − 2 lim e−R (−R − 1) − 2 2 R→∞ 2
r R→∞ r √ R
1 1 = lim 2 x
=0− 2 =− 2 R→∞ √ 2 √
r r
= lim (2 R − 2 2) = ∞
R→∞
Therefore, for all r < 0 the integral
∞ ∞
x
xerx dx converges. So dx diverges.
0 2 x3/2 − 1


2 + sec2 x 1 ∞ R
24. ≥ ex dx = lim ex dx
x x 2 R→∞ 2
∞ R R
1 1 = lim ex
dx = lim dx R→∞ 2
1 x R→∞ 1 x
R = lim (eR − e2 ) = ∞
= lim ln |x||1 = lim ln |R| = ∞ R→∞
R→∞ R→∞ ∞
∞ 2 x2 ex
2 + sec x So dx diverges.
So dx diverges. 2 ln x
1 x
2
3 3 30. ex +x+1
> ex
25. 0 < < x ∞ R
x + ex e x
e dx = lim ex dx
∞ R
3 3 1 R→∞ 1
x
dx = lim dx R
0 e R→∞ 0 ex = lim ex = lim (eR − e) = ∞
R R→∞ 1 R→∞
3 ∞
= lim − x So e x2 +x+1
dx diverges.
R→∞ e 0
1
3
= lim − R + 3 = 3
R→∞ e 31. Let u = ln 4x, dv = xdx
∞
3 dx x2
So dx converges. du = ,v =
0 x + ex x 2
1 1
3
26. e−x < e−x x ln 4xdx = x2 ln 4x − xdx
∞ R 2 2
e−x dx = lim e−x dx 1 2 x2
1 R→∞ 1 = x ln 4x − +c
R 2 4
= lim −e−x = lim −e−R + e−1 1 1
R→∞ 1 R→∞ I= x ln 4xdx = lim x ln 4xdx
−1 R→ 0+
=e . 0 R
∞ 1
So
3
e−x dx converges. 1 2 x2
= x ln 4x −
lim +
1 R→ 0 2 4 R
2 1 1 2 R2
sin x 1 1 = − − lim R ln 4R −
27. x
≤ x
< x 4 R→ 0+ 2 4
1+e 1+e e 1 1
∞ R
1 1 =− − lim R2 ln 4R
dx = lim dx 4 2 R→ 0+
0 ex R→∞ 0 ex ln 4R
R lim R2 ln 4R = lim + −2
= lim (−e−x ) R→ 0+ R→ 0 R
R→∞ 0 R−1 R2
= lim (−e−R + 1) = 1 = lim + −3
= lim + =0
R→∞ R→ 0 −2R R→ 0 −2
∞
sin2 x 1
So dx converges. Hence I = −
1 + ex 4
0

ln x x 32. Let u = x, dv = e−2x dx
28. x < x 1
e +1 e du = dx, v = − e−2x
∞
x R 2
dx = lim xe−x dx x 1
ex R→∞ xe−2x dx = − e−2x + e−2x dx
2 2
R
2 2
= lim (−xe−x − e−x ) x
R→∞ = − e−2x − e−2x
2 2
= lim e−R (−R − 1) + 3e−2 ∞ R
R→∞
and lim e −R
(−R − 1) xe−2x dx = lim xe−2x dx
R→∞ 0 R→∞ 0
−R − 1 −1 R
= lim = lim R = 0 x
R→∞ e R R→∞ e = lim − e−2x − e−2x
∞
ln x R→∞ 2 0
So dx converges. = lim e−2R (−R/2 − 1) + 1
2 ex + 1 R→∞
−R/2 − 1
x2 ex = lim +1
29. > ex R→∞ e2R
ln x


−2 Since the graph of the function xe−x is
2
= lim +1=1
R→∞ 2e2R anti-symmetric across the y-axis,
2 0 2 R
33. The volume is ﬁnite:
∞ R
lim xe−x + xe−x =0
1 1 R→∞ −R 0
V =π dx = π lim dx Then we have
1 x2 R→∞ 1 x2 ∞
2
∞
2
1
R e−x dx = 2 x2 e−x dx
= π lim − −∞ −∞
R→∞ x 1 And the conclusion is
√
∞
2 −x2 π
1 x e dx =
= π lim −
+1 =π −∞ 2
R→∞ R
The surface area is inﬁnite:
∞
1 1 40. (a) Since k > 0, we have
∞ ∞
S = 2π 1 + 4 dx sin kx sin kx
1 x x dx = (k) dx
0 x 0 kx
1 1 1 Let u = kx, du = kdx.
1+ 4 > ∞
x x x sin u π
∞ R
= du = .
1 1 0 u 2
and dx = lim dx
1 x R→∞ 1 x (b) Since k < 0 , assume k = −m , where
R m ∞ 0.
> ∞
= lim ln |x| = lim ln R = ∞ sin kx sin (−m) x
R→∞ 1 R→∞ dx = dx
0 x 0 x
∞
∞
34. The integral x3 dx diverges: sin mx
=− dx
−∞
0 x
∞ R ∞
sin mx
x3 dx = lim x3 dx =− (m) dx
0 R→∞ 0 0 mx
R
x4 R4 Let u = mx, so that du = mdx.
= lim = lim =∞ ∞
R→∞ 4
0
R→∞ 4 sin u π
R =− du = − .
0 u 2
The limit lim x3 dx = 0:
R→∞ −R (c) Since k > 0 , we have
R R ∞ ∞
x4 sin2 kx sin2 kx 2
lim x3 dx = lim dx = 2 k dx
R→∞ −R R→∞ 4
−R 0 x2 0 (kx)
4 4 Let u = kx, du = kdx.
R R
= lim − = lim 0 = 0 ∞
sin u π
R→∞ 4 4 R→∞ = kdu = k .
0 u 2
35. True, this statement can be proved using the
integration by parts: (d) Since k < 0, assume k = −m, where
f (x)dx = xf (x) − g(x)dx, m > 0.
∞ ∞
sin2 kx sin2 [(−m) x]
where g(x) is some function related to f (x). dx = dx
0 x2 0 x2
∞
1 sin2 mx
36. False, consider f (x) = = dx
x 0 x2
∞ 2
sin mx 2
37. False, consider f (x) = ln x = 2 m dx
0 (mx)
38. True, this statement is best understood graph- Let u = mx, du = mdx.
∞
ically. sin2 u π kπ
= m du = m = − .
√ 0 u2 2 2
39. (a) Substitute u = kx √
∞ ∞
2 1 2 π x 1
e−kx dx = √ e−u du = √ 41. Since ≈ 4,
−∞ k −∞ k x5 + 1 x
∞ ∞
(b) We use integration by parts x 1
2 dx ≈ dx.
(u = e−x , v = x): 1 x5 + 1 1 x4
∞
2 2 2 1 1
e−x dx = xe−x + 2 x2 e−x dx we have dx converges to - .
1 x4 3


∞ π/2
x
Hence dx also converges. = ln(sin x cos x)dx
1 +1 x5 0
x 1 π/2
Let f (x) = 5 and g(x) = 4 .
x +1 x = [ln(sin(2x)) − ln 2]dx
So that, we have, 0 < f (x) < g(x) . 0
π/2
By Comparison test, π
∞ ∞ = ln(sin(2x))dx − ln 2
x 1 1 0 2
dx < dx = − . 1 π π
1 x5 + 1 1 x4 3 = ln(sin x)dx − ln 2
2 0 2
1 x Hence,
42. (a) Let f (x) = √ and g(x) = √ . π/2
x 2 x 3−1
So that, we have, 0 < f (x) < g(x). 2 ln(sin x)dx
0
By Comparison test, π
∞ ∞
1 π
1 x = ln(sin x)dx − ln 2
√ dx < √ dx, and 2 0 2
x2 x 3−1 On the other hand, we notice that the graph of
2 2
1 sin x is symmetric over the interval [0, π] across
f (x) = √ diverges.
x2 the line x = π/2, hence
x π π/2
Hence g(x) = √ also diverges.
x3 − 1 ln(sin x)dx = 2 ln(sin x)dx
0 0
x 1 and then
(b) Let f (x) = √ and g(x) = 5/4 .
x5 − 1 x 1 π π/2

So that, we have, 0 < f (x) < g(x) . ln(sin x)dx = ln(sin x)dx
2 0 0
By Comparison test, π/2
π
∞ ∞
x 1 So we get ln(sin x)dx = − ln 2
√ dx < 5/4
dx, and 0 2
2 x 5−1
2 x
1 1 1
g(x) = 5/4 converges. n n
x 44. (ln x) dx = lim (ln x) dx
x 0
+ t→0 t
Hence f (x) = √ also converges. 1
x 5−1 n 1 n−1
= lim x(ln x) |t −n (ln x) dx
x t→0+ t
(c) Let f (x) = √ and Using#112 from the table.
x 5+x−1
2
x = lim 0 − t(ln t)
g(x) = √ . + t→0
x5 − 1 1
n−1
So that, we have, 0 < f (x) < g(x) . − lim n (ln x) dx
By Comparison test, t→0+ t
∞ ∞ 1
x x n−1
√ dx < √ dx , = 0 − lim n
+
(ln x) dx .
x 5+x−1 x 5−1 t→0 t
2 2
x Continuing in the same manner,
and g(x) = √ converges. 1
x5 − 1 n
x (ln x) dx
Hence f (x) = √ also con- 0
x 5+x−1 1
verges. = (−1)
n−1
n! lim (ln x) dx
t→0+ t
π 1
43. Substitute u = −x n−1
2 = (−1) n! lim (x ln x − x)
π/2 0 t→0+ t
ln(sin x)dx = − ln(sin(π/2 − u))du n−1
0 π/2 = (−1) n! lim ((0 − t ln t) − (1 − t))
π/2 π/2 t→0+
n
= ln(cos u)du = ln(cos x)dx = (−1) n!.
0 0
Moreover,
π/2
2 ln(sin x)dx 45. Improper because tan(π/2) is not deﬁned. The
0 two integrals
π/2 π/2 π/2 π/2
1
= ln(cos x)dx + ln(sin x)dx dx = f (x)dx
0 0 0 1 + tan x 0
π/2 because the two integrand only diﬀer at one
= [ln(cos x) + ln(sin x)] dx value of x, and that except for this value, ev-
0


erything is proper. 1 2
 tan x = − x3 e−x
π 2
 if 0 ≤ x < 3 1 2 1 2
g(x) = 1 + tan x 2 + − xe−x + e−x dx
 0 if x = π 2 2 2
2 1 2 3 2 3 2
π = − x3 e−x − xe−x + e−x dx
Substitute u = x − followed by w = −u 2 4 4
2 Putting integration limits to all the above, and
π/2 0 realizing that when taking limits to ±∞, all
1 1
dx = du 2
multiples of e−x as shown in above will go
0 1 + tan x −π/2 1 − cot u
0
1 to 0 (we have seen this a lot of times before).
=− dw Then we get
π/2 1 + cot w ∞
2 3 ∞ −x2 3√
π/2
1 x4 e−x dx = e dx = π
= 4 −∞ 4
cos w dw −∞
0 1+ This means when n = 2, the statement
sin w ∞
π/2 2 (2n − 1) · · · 3 · 1 √
sin w x2n e−x dx = π
= dw −∞ 2n
0 sin w + cos w
π/2 is true. (We can also check that the case for
tan w
= dw n = 1 is correct.) For general n, supposing
0 tan w + 1 that the statement is true for all m < n, then
π/2
tan x integration by parts gives
= dx
tan x + 1 2
0 x2n e−x dx
Moreover,
π/2
tan x π/2
1 1 2 2n − 1 2

dx + dx = − x2n−1 e−x + x2n−2 e−x dx
tan x + 1 1 + tan x 2 2
0 0
π/2 and hence
∞
tan x 1 2
= + dx x2n e−x dx
0 1 + tan x 1 + tan x −∞
π/2 π/2 π 2n − 1 ∞ 2n−2 −x2
= 1 dx = x = = x e dx
0 0 2 2 −∞
π/2
1 1 π π 2n − 1 (2n − 3) · · · 3 · 1 √
Hence dx = = = · π
1 + tan x 2 2 4 2 2n−1
0 (2n − 1) · · · 3 · 1 √
= π
46. As in exercise.45, We have 2n
π/2 π/2 √
1 tank x 48. Substitute u = ax
dx = dx
1 + tan xk
1 + tank x 2 1 2
0
hence,
0 e−ax dx = √ e−u du
a
π/2
1 and then
2 dx ∞
1 ∞
π
0 1 + tank x 2
e−ax dx = √
2
e−u du =
π/2
1 π/2
tank x −∞ a −∞ a
= dx + dx Ignoring issues of convergence, the derivatives
0 1 + tank x 0 1 + tank x
π/2 can be taken from the integrand, we get the
π
= 1dx = following:
0 2 1st derivative
therefore, d ∞
2 d π
π/2
1 π e−ax dx =
dx = da −∞ da a
0 1 + tank x 4 ∞
2 1 π
− x2 e−ax dx = −
47. Use integration by parts twice, ﬁrst time −∞ 2 a3
1 2 2nd derivative
let u = − x3 , dv = ds − 2xe−x dx d2 ∞
d2 π
2 2
e−ax dx = 2
second time da −∞2 da a
1 2
let u = − x, dv = −2xe−x dx ∞
2 3 π
2 x4 e−ax dx =
2 4 a5
x4 e−x dx −∞
. . . nth derivative
∞
1 3 2 −x2 dn 2 dn π
e−ax dx = n
2
= − x3 e−x + x e dx n
2 2 da −∞ da a


∞ R
(−1)n
2
x2n e−ax dx k
= lim ue−u dx
−∞ r2 R→∞ 0
(2n − 1) · · · 3 · 1 π R
= (−1)n k
2n a2n+1 = 2 lim (ue−u + e−u )
r R→∞ 0
Setting a = 1, we get the result of Exercise 47. k R+1 k
∞ R
= 2 lim −1 =− 2 =1
r R→∞ eR r
49. (a) ke−2x dx = lim ke−2x dx So k = −r2
0 R→∞ 0
R If r ≤ 0:
k −2x ∞
= − lim e
2 R→∞ 0 The integral kxe−rx dx diverges for
k −2R k 0
= − lim (e − 1) = = 1 any value of k, so there is no value of k to
2 R→∞ 2
So k = 2 make the function f (x) = k a pdf.
∞ R
(b) ke−4x dx = lim ke−4x dx 51. From Exercise 49 (c) we know that this r has
0 R→∞ 0 to be positive.
R
k −4x Substitute u = rx
∞ ∞
=− lim e
4 R→∞ 0 µ= xf (x)dx = rxe−rx dx
k −4R k 0 0
= − lim (e − 1) = = 1 R
4 R→∞ 4 = lim rxe−rx dx
So k = 4 R→∞ 0
R
(c) If r > 0: 1
∞ R = lim ue−u du
r R→∞ 0
ke−rx dx = lim ke−rx dx R
R→∞ 1
0
R
0
= lim e−u (−u − 1)
k −rx r R→∞ 0
=− lim e −R − 1 1 1 1
r R→∞ 0 = lim + =0+ =
k −rR k R→∞ eR r r r
=− lim (e − 1) = = 1
r2 R→∞ r
So k = r 52. From Exercise 50 (c) we know that this r has
50. (a) Substitute u = 2x to be positive.
∞ R Substitute u = rx
∞ ∞
kxe−2x dx = lim kxe−2x dx µ= xf (x)dx = r2 x2 e−rx dx
0 R→∞ 0
R 0 0
k R
= lim ue−u dx = lim 2 2 −rx
r x e dx
4 R→∞ 0 R→∞
R 0
k 1 R
= lim (ue−u + e−u ) = lim u2 e−u du
4 R→∞ 0 r R→∞ 0
k R+1 k 1 R
= lim R
−1 =− =1 = lim e−u (−u2 − 2u − 2)
4 R→∞ e 4 r R→∞ 0
So k = −4 −R2 − 2R − 2 2 2 2
= lim R
+ =0+ =
(b) Substitute u = 4x R→∞ e r r r
∞ R
35
kxe−4x dx = lim kxe−4x dx 1 −x/40 35
0 R→∞ 0
53. e dx = −e−x/40 = 1 − e−35/40
R 0 40 0
k
= lim ue−u dx P (x > 35) = 1 − above = e−35/40
16 R→∞ 0
R 40
k 1 −x/40 40
= lim (ue−u + e−u ) e dx = −e−x/40 = 1 − e−40/40
16 R→∞ 0 0 40 0
k R+1 k
= lim −1 =− =1 P (x > 40) = 1 − above = e−40/40
16 R→∞ eR 16
45
So k = −16 1 −x/40 45
e dx = −e−x/40 = 1 − e−45/40
(c) If r > 0: 0 40 0
Substitute u = rx P (x > 45) = 1 − above = e−45/40
∞ R
kxe−rx dx = lim kxe−rx dx Hence,
0 R→∞ 0


P (x > 40) R
P (x > 40|x > 35) = = lim 2xe−2x dx
P (x > 35) R→∞ 0
e−40/40 R
= = e−5/40 ≈ 0.8825 = lim e−2x (−x − 1/2)
e−35/40 R→∞ 0
P (x > 45) −2R 1 1
P (x > 45|x > 40) = = lim e (R + 1/2) + =
P (x > 40) R→∞
∞
2 2
e−45/40 µ2 = xf2 (x)dx
= −40/40 = e−5/40 ≈ 0.8825
e −∞
1 1
x2
= xdx =
54. (a) Following Exercise 53, we get 0 2 0
P (x > m + n) 1
P (x > m + n|x > n) = =
P (x > n) 2
m+n 1 −x/40
µ1 = µ2 and when r = 1/2
1− 0 40 e dx e−2·1/2
= m 1 −x/40 Ω1 (1/2) = =1
1− 0 40 e dx 2 · 1/2 + e−2·1/2 − 1
1 − 2 · 1/2 + (1/2)2
e−(m+n)/40 Ω2 (1/2) = =1
= = e−m/40 (1/2)2
e−n/40
A (d) The graph of f2 (x) is more stable than
A
(b) ce−cx dx = −e−cx 0
= 1 − e−cA that of f1 (x).
0 f1 (x) > f2 (x) for 0 < x < 0.34
P (x > m + n)
P (x > m + n|x > n) = and f1 (x) < f2 (x) for x > 1.
P (x > n)
m+n
1− 0 ce−cx dx e−c(m+n) 2r − 1
= m = (e) Ω1 (r) = 1 −
1 − 0 ce−cx dxdx e−cn e−2r
+ 2r − 1
−cm 2r − 1
=e Ω2 r = 1 −
r2
55. (a) For x ≥ 0, and
x x r2 − (e−2r + 2r − 1) = e−2r + (r − 1)2 > 0
F1 (x) = f1 (t)dt = f1 (t)dt This means
−∞ 0
x x when r < 1/2, Ω1 (r) < Ω2 (r)
= 2e−2t dt = −e−2t = 1 − e−2x when r > 1/2, Ω1 (r) > Ω2 (r)
0 0
∞
[1 − F1 (x)]dx In terms of this example, we see that the
r
Ω1 (r) = r riskier investment is only disadvantageous
−∞ 1
F (x)dx when r small, and will be better when r
∞ −2x
r
e dx large.
= r
0
(1 − e−2x )dx
1 −2r 56. Following Exercise 54(b),
2e e−2r R(t) = P (x ≥ t) = P (x > t)
= 1 −2r 1 = 2r + e−2r
r + 2e −2 −1 t t
x =1− f (x)dx = 1 − ce−cx dx
0 0
(b) For 0 ≤ x ≤ 1, F2 (x) = f2 (t)dt = 1 − (1 − e−ct ) = e−ct
−∞
x x x
= f2 (t)dt = 1 dt = t =x 57. Graph of p1 (x):
0 0 0
∞
r
[1 − F2 (x)]dx 1 1
Ω2 (r) = r p1 (x) dx = 1dx = 1,
−∞ 2
F (x)dx 0 0
1 1 r2
r
(1 − x)dx 2 −r+ 2
Graph of p2 (x):
= r = r2
0
xdx 2
1 − 2r + r 2 Similarly,
= 1 1/2 1
r2 p2 (x) dx = 4xdx + (4 − 4x) dx
∞ 0 0 1/2
(c) µ1 = xf1 (x)dx 1/2 1
= 2x2 0 + 4x − 2x2 1/2
−∞
∞
1 1
= 2xe−2x dx = − 0 + (4 − 2) − 2 − = 1.
0 2 2


The Boltzmann integral Ch. 6 Review Exercises
1
I(p1 ) = p1 (x) ln p1 (x) dx √
0
1. Substitute u = x
√
1 e x √
= 1 ln 1dx = 0. √ dx = 2 eu du = 2eu + c = 2e x + c
0
x
1
Also, I(p2 ) = p2 (x) ln p2 (x) dx 1
0
2. Substitute u =
1/2 x
sin(1/x)
= 4x ln (4x) dx dx = − sin u du
0 x2
1
= cos u + c = cos(1/x) + c
+ (4 − 4x) ln (4 − 4x) dx
1/2
Let u = 4x, du = 4dx 3. Use the table of integrals,
x2 1 1
and t = 4 − 4x, dt = −4dx √ dx = − x 1 − x2 + sin−1 x + c
1 2 1 0 1−x 2 2 2
= u ln udu − t ln tdt
4 0 4 2 4. Use the table of integrals,
2
1 1 2 1 2 x
= u ln u − u2 √ dx = 2 sin−1 + c
2 2 4 0 9 − x2 3
1
= (2 ln 2 − 1) = 0.193147. 5. Use integration by parts, twice:
2
1 x2 e−3x dx
For the pdf p2 (x) , the probability at x = is
2 1 2
1 = − x2 e−3x + xe−3x dx
maximum which is equal to .The probability 3 3
2 1
decreases as x tends to 0 or 1. = − x2 e−3x
3
2 1 1
 1 + − xe−3x + e−3x dx
 2x 0≤x< 3 3 3
4

 1 2 2
= − x2 e−3x − xe−3x − e−3x + c

1 1


 10x − 2 ≤x< 3 9 27


p3 (x) = 4 2
 8 − 10x 1 3 6. Substitute u = x3
 ≤x< 1 1 −x3
2 4 3
x2 e−x dx = e−u du =

e +c




 2 − 2x 1 3 3
<x≤1

4
7. Substitute u = x2
Graph of p3 (x): x 1 du
1 1/4 1/2 dx =
1 + x4 2 1 + u2
p3 (x) dx = 2xdx + (10x − 2)dx 1 1
0 0 1/4 = tan−1 u + c = tan−1 x2 + c
3/4 1 2 2
+ (8 − 10x)dx + (2 − 2x) dx
1/2 3/4 x3 1
= 1. 8. dx = ln(1 + x4 ) + c
1 + x4 4
Also, The Boltzmann integral x3 1
1 9. 4
dx = ln(4 + x4 ) + c
I(p3 ) = p3 (x) ln p3 (x) dx 4+x 4
0
1/4 10. Substitute u = x2
= 2x ln (2x) dx x 1 du
0 dx =
1/2 4 + x4 2 4 + u2
+ (10x − 1) ln(10x − 1)dx 1 u 1 x2
1/4
= tan−1 + c = tan−1 +c
4 2 4 2
3/4
+ (8 − 10x) ln(8 − 10x)dx x3
1/2 11. e2 ln x dx = x2 dx = +c
1 3
+ (2 − 2x) ln (2 − 2x) dx
3/4 1
= 0.42. 12. cos 4x dx = sin 4x + c
4

CHAPTER 6 REVIEW EXERCISES 401

π/4 π/4
13. Integration by parts, 1
1 20. sin x cos x dx = sin 2x dx
0 0 2
x sin 3x dx π/4
0
1 1
1 1 = − cos 2x =
1 1 4 0 4
= − x cos 3x + cos 3x dx
3 0 3 0 21. Substitute u = sin x
1 1 1
= − cos 3 + sin 3x cos x sin2 x dx = u2 du
3 9 0
1 1 u3 sin3 x
= − cos 3 + sin 3 = +c= +c
3 9 3 3

14. Substitute u = x2 22. Substitute u = sin x
1 1
1 cos x sin3 x dx = u3 du
x sin 4x2 dx = sin 4u du
0 0 2 u4 sin4 x
1 1 1 = +c= +c
= − cos 4u = (1 − cos 4) 4 4
8 0 8
15. Use the table of integrals 23. Substitute u = sin x
π/2
4
cos3 x sin3 x dx = (1 − u2 )u3 du
sin x dx
0 u4 u6 3 sin4 x − 2 sin6 x
1 π/2 = − +c= +c
= − sin3 x cos x 4 6 12
4 0
3 x 1 π/2 24. Substitute u = cos x
+ − sin x cos x
4 2 2 0 cos4 x sin3 x dx = − u4 (1 − u2 ) du
3π
= u5 u7 −7u5 + 5u7
16 =− + +c= +c
5 7 35
16. Use the table of integrals
π/2 25. Substitute u = tan x
cos3 x dx
0
tan2 x sec4 x dx = u2 (1 + u2 ) du
2 1 π/2 2
= sin x + sin x cos2 x = u3 u5 5 tan3 x + 3 tan5 x
3 3 0 3 = + +c= +c
3 5 15
17. Use integration by parts, 26. Substitute u = tan x
1
x sin πx dx tan3 x sec2 x dx = u3 du
−1
1 1 1 1 u4 tan4 x
= − x cos πx + cos πx dx = +c= +c
π −1 π −1 4 4
2 1 1 2
= + 2 sin πx = 27. Substitute u = sin x
π π −1 π √
sin x cos3 x dx
18. Use integration by parts, twice
1 2 3/2 2 7/2
x2 cos πx dx = u1/2 (1 − u2 ) du = u − u +c
0
3 7
1
1 2 1 2 2 2
= x sin πx − x sin πx dx = sin3/2 x − sin7/2 x + c
π 0 π 0 3 7
1
2 1 1 1 28. Substitute u = sec x
=− − x cos πx + cos πx dx
π π 0 π 0 tan3 x sec3 x dx = (u2 − 1)u2 du
2 1 1 1 2
=− + 2 sin πx =− u5 u3 3 sec5 x − 5 sec3 x
π π π π2 = − +c= +c
0 5 3 15
19. Use integration by parts 29. Complete the square,
2 2 2
x4 2 1
x3 ln x dx = ln x − x3 dx dx
1 4 1 4 1
8 + 4x + x2
x4 2 15 2 x+2
= 4 ln 2 − = 4 ln 2 − = dx = tan−1 +c
16 1 16 (x + 2)2 + 22 2


30. Complete the square, 3 3
= + dx
3 x−3 x+4
√ dx
−2x − x2 = 3 ln |x − 3| + 3 ln |x + 4| + c
3
= dx = 3 sin−1 (x − 1) + c 39. Use the method of PFD
1 − (x − 1)2 4x2 + 6x − 12
dx
31. Use the table of integrals, x3 − 4x
√ 3 −1 2
2 4 − x2 = + + dx
√ dx = − +c x x+2 x−2
x2 4 − x2 2x
= 3 ln |x| − ln |x + 2| + 2 ln |x − 2| + c
32. Substitute u = 9 − x2
x 1 du 40. Use the method of PFD
√ dx = − 5x2 + 2 2 3x
9 − x2 2 u1/2 dx = + dx
x3 + x x x2 + 1
1 1 3
= − u3/2 + c = − (9 − x2 )3/2 + c = 2 ln |x| + ln(x2 + 1) + c
3 3 2
33. Substitute u = 9 − x2 41. Use the table of integrals,
x3 1 (9 − u)
√ dx = − du ex cos 2x dx
9−x 2 2 u1/2
9 1 (cos 2x + 2 sin 2x)ex
=− u−1/2 du + u1/2 du = +c
2 2 5
1
= −9u1/2 + u3/2 + c
3 42. Substitute u = x2 followed by integration by
1 parts
= −9(9 − x ) + (9 − x2 )3/2 + c
2 1/2
3 1
x3 sin x2 dx = u sin u du
34. Substitute u = x2 − 9 2
1 1
x3 1 = − u cos u + cos u du
√ dx = (u + 9)u−1/2 du 2 2
x2 − 9 2 1 1
1 = − u cos u + sin u + c
= u3/2 + 9u1/2 + c 2 2
3 1 1
= − x2 cos x2 + sin x2 + c
1 2 2
= (9 − x2 )3/2 + 9(9 − x2 )1/2 + c
3 43. Substitute u = x2 + 1
1
35. Substitute u = x2 + 9 x x2 + 1 dx = u1/2 du
2
x3 1 1 1
√ dx = (u − 9)u−1/2 du = u3/2 + c = (x2 + 1)3/2 + c
x2 + 9 2 3 3
1
= u3/2 − 9u1/2 + c 44. Use the table of integrals
3
1 2 1 − x2 dx
= (x + 9)3/2 − 9(x2 + 9)1/2 + c
3 1 1
= 1 − x2 + sin−1 x + c
36. Substitute u = x + 9 2 2
4 du
√ dx = 4 √ 4 A B
x+9 u 45. = +
√ x2 − 3x − 4 x+1 x−4
= 8u1/2 + c = 8 x + 9 + c 4 = A(x − 4) + B(x + 1)
= (A + B)x + (−4A + B)
37. Use the method of PFD 4 4
x+4 A = − ;B =
dx 5 5
x2 + 3x + 2 4 −4/5 4/5
3 −2 = +
= + dx x2 − 3x − 4 x+1 x−4
x+1 x+2
= 3 ln |x + 1| − 2 ln |x + 2| + c 2x A B
46. = +
x2 + x − 6 x−2 x+3
38. Use the method of PFD
5x + 6 2x = A(x + 3) + B(x − 2)
dx = (A + B)x + (3A − 2B)
x2 + x − 12


4 6
A= ;B = 53. sec4 x dx
5 5
2x 4/5 6/5 1 2
= + = sec2 x tan x + sec2 x dx
x2 + x − 6 x−2 x+3 3 3
1 2
−6 A B C = sec2 x tan x + tan x + c
47. = + + 3 3
x3 + x2 − 2x x x−1 x+2
− 6 = A(x − 1)(x + 2) + Bx(x + 2) + cx(x − 1)
54. tan5 x dx
A = −3; B = −2; C = −1
−6 −3 −2 −1 1
= + + = tan4 x − tan3 x dx
x3 + x2 − 2x x x−1 x+2 4
1 1
x2 − 2x − 2 A Bx + c = tan4 x − tan2 x + tan x dx
48. = + 2 4 2
x3 + x x x +1 1 1
= tan4 x − tan2 x − ln | cos x| + c
x2 − 2x − 2 = A(x2 + 1) + (Bx + c)x 4 2
= (A + B)x2 + cx + A 55. Substitute u = 3 − x
A = −2; B = 3; C = −2 4 1
dx = −4 du
x2 − 2x − 2 −2 3x − 2 x(3 − x)2 (3 − u)u2
3+x
= + 2
x x x +1 4 3−u 4
= ln + +c
x−2 A B 9 u 3u
49. = +
x2 + 4x + 4 x + 2 (x + 2)2 4 x 4
x − 2 = A(x + 2) + B = ln + +c
9 3−x 3(3 − x)
A = 1; B = −4
x−2 1 −4 56. Substitute u = sin x
= + cos x du
x2 + 4x + 4 x + 2 (x + 2)2 dx =
2 u2 (3 + 4u)
sin x(3 + 4 sin x)
x2 − 2 Ax + B Cx + D
50. = 2 + 2 4 3 + 4u 1
(x 2 + 1)2 x +1 (x + 1)2 = ln − +c
9 u 3u
x2 − 2 = (Ax + B)(x2 + 1) + cx + D 4 3 + 4 sin x 1
A = 0; B = 1; C = 0; D = −3 = ln − +c
9 sin x 3 sin x
x2 − 2 1 −3
= 2 + 2 √ 9
(x 2 + 1)2 x + 1 (x + 1)2 2 + x2
9 + 4x2 4
57. 2
dx = dx
51. Substitute u = e2x x x2 
e3x 4 + e2x dx 9 2
− 4 + x 
1 = 2
 + ln x + 9/4 + x2 +c
= e 2x
4e2x + e4x dx = 4u + u2 du x 
2
1 √
= (u + 2)2 − 4 du 9 + 4x2 9
2 =− + 2 ln x + + x2 + c
1 x 4
= (u + 2) (u + 2)2 − 4
4
− ln |(u + 2) + (u + 2)2 − 4| + c x2 1 x2
58. √ dx = dx
√ 4 − 9x 2 3 4/9 − x2
(e2x + 2) 4e2x + e4x
= 1 2 3x
4 = − x 4/9 − x2 + sin−1 +c
− ln (e2x + 2) + 4e2x + e4x + c 6 27 2
√
4 − x2
52. Substitute u = x2 59. dx
1 x
√
x x4 − 4 dx = u2 − 4 du 2 + 4 − x2
√ 2 = 4 − x2 − 2 ln +c
u u2 − 4 x
= − ln |u + u2 − 4| + c
√4
x2 x4 − 4 x2 1 1
= − ln |x2 + x4 − 4| + c 60. dx = dx
4 (x6 − 4)3/2 3 (u2 − 4)3/2


1 2 sec θ tan θ So the original integral diverges.
= dx
3 (4 sec2 θ − 4)3/2
2 2
1 sec θ tan θ x dx x dx
= dx 68. = lim
3 tan3 θ 1 1 − x2 R→1 +
R 1 − x2
2
1 x3 1 2
= csc θ cot θ dx = − √ +c = lim+ − ln |1 − x | = ∞
3 3 x6 − 4 R→1 2 R
61. Substitute u = x2 − 1 So the original integral diverges.
1 0
x du
dx = 69. If c(t) = R, then the total amount of dye is
0 x2 − 1 −1 2u
R T T
du 0
= lim = lim− ln |u| c(t) dt = R dt = RT
R→0− −1 2u R→0 −1 0 0
2T t
This limit does not exist, so the integral di- If c(t) = 3te , then we can use integration by
verges. parts to get
T
62. Substitute u = x − 4 3te2T t dt
10 6
2 dx 2 du 0
√ = √ T
4 x−4 0 u 3t 2T t T 3 2T t
6 6
= e − e dt
2T 0 2T
= lim+ 2u−1/2 du = lim+ 4u1/2 0
T
R→0 R R→0 R 3 2 3 2T t
√
√ √ = e2T − e
= lim+ (4 6 − 4 R) = 4 6 2 4T 2 0
R→0 3 2 3 2T 2 3
= e2T − e +
∞
3 R
3 2 4T 2 4T 2
63. 2
dx = lim dx Since R = c(T ) = 3T e2T
2

1 x R→∞ 1 x2
R
3 3 The cardiac output is
= lim − = lim − + 3 = 3 2
R→∞ x 1 R→∞ R RT 3T 2 e2T
T
= 3 2T 2 3 3
64. Use integration by parts, c(t) dt 2e − 4T 2 e2T 2 + 4T 2
0
∞ R RT 3
xe−3x dx = lim xe−3x dx = 2 e2T 2 /2 − 3e2T 2 /4 + 3/4
1 R→∞ 1 3T
R
−3x x 1 70. With u = ln(x + 1) and v = x
= lim e − −
R→∞ 3 9 1
R 1 4e−3 ln x + 1 dx
= lim e−3R − − +
R→∞ 3 9 9 x
−3 = x ln(x + 1) − dx
4e x+1
= 1
9 = x ln(x + 1) − 1− dx
∞ R x+1
4 4
65. 2
dx = lim dx = x ln(x + 1) − x + ln(x + 1) + c
0 4+x R→∞ 0 4 + x2
x R With u = ln(x + 1) and v = x + 1
= lim 2 tan−1 = lim 2 tan−1 R = π
R→∞ 2 0 R→∞ ln x + 1 dx
R
∞
e−x
2
1 x+1
66.
2
xe−x dx = lim − = = (x + 1) ln(x + 1) − dx
R→∞ 2 2 x+1
0
0
0
= (x + 1) ln(x + 1) − x + c
0 −x2
2 e 1 The two answers are the same.
xe−x dx = lim − =−
−∞ R→∞ 2 2 en
−R 1
∞
2 1 1 71. fn,ave = n ln x dx
So xe−x dx = − =0 e 0
2 2 en
−∞ 1
= lim ln x dx
32
3 2 en R→0 R
67. dx = lim+ dx 1 en
0 x2 R→0 R x2 = n lim (x ln x − x)
2 e R→0 R
3 1
= lim+ − =∞ n n
= n lim (ne − e − R ln R + R) = n − 1
R→0 x R e R→0


72. First we notice that So we want to ﬁnd the value of a so that
P (t < x < t + ∆t) a − 90
lim √
∆t→0 ∆t 450 e−u2 du = 0.49√π
t+∆t
1 0
= lim f (x) dx = f (t)
∆t→0 ∆t t Using a CAS we ﬁnd
a − 90
And then the failure rate function √ ≈ 1.645, a ≈ 125
P (x < t + ∆t|x > t) 450
lim
∆t→0 ∆t Some body being called a genius need to have
1 P (t < x < t + ∆t) a IQ score of at least 125.
= lim
∆t→0 ∆t P (x > t) ∞
P (t < x < t + ∆t) 1 f (t) 1 ∞ π
= lim · = 76. I (1) = dx = tan−1 x =
∆t→0 ∆t R(t) R(t) 0 (1 + x2 ) 0 2
Now, I (n + 1)
t ∞
1 1
73. R(t) = P (x > t) = 1 − ce−cx dx = n dx
0 (1 + x2 ) (1 + x2 ) 0
t  −n
 
= 1 − (−e−cx ) = 1 − (1 − e−ct ) = e−ct ∞ d 1 + x2 1 
0 −  dx dx
0 dx (1 + x2 )
Hence

f (t) ce−ct tan−1 x
∞ ∞
xtan−1 x
= −ct = c = + 2n
R(t) e n n dx
(1 + x2 ) 0 0 (1 + x2 )
∞
s xtan−1 x
⇒ I (n + 1) = 2n n dx ... (1)
74. (a) P (x > s) = 1 − xe−x dx 0 (1 + x2 )
∞
0
s 1 + x2 − x2
= 1 − (−xe−x − e −x
) Also, I (n + 1) = n+1 dx
0 0 (1 + x2 )
∞
= 1 − (1 − se−s − e−s ) x2
= I (n) − n+1 dx
= (s + 1)e−s 0 (1 + x2 )
∞
P (x > s + t|x > s) 1 x2
P (x > s + t) = I (n) − n dx
= (1 + x2 ) (1 + x2 ) 0
P (x > s)  −n
 
∞ d 1 + x2 x 2
(s + t + 1)e−s−t

t − dx dx
= −s
= e−t + e−t 
dx (1 + x2 )
(s + 1)e 1+s 0 
∞
(b) Take the derivative w.r.t s: x − tan−1 x
d t t = I (n) − n+1
e−t + e−t = −e−t (1 + x2 ) 0
ds 1+s (1 + s)2 ∞
When t > 0, since e−t > 0 and x x − tan−1 x
+2n n+1 dx
(1 + s)2 > 0, the above derivative is neg- 0 (1 + x2 )
∞
ative, so the function P (x > s + t|x > s) x2 − xtan−1 x
is decreasing w.r.t. s. ds = I (n) − 2n n+1 dx
0 (1 + x2 )
∞
x2
75. We use a CAS to see that = I (n) − 2n n+1 dx
100
1 2 0 (1 + x2 )
√ e−(x−100) /450 dx ≈ 24.75% ∞
xtan−1 x
90 450π + 2n n+1 dx
0 (1 + x2 )
We can use substitution to get
∞ Therefore,
1 2
√ e−(x−100) /450 dx I(n + 1) = I (n)
450π a ∞
1 ∞
−u2
x2
=√ a − 90 e du −2n n+1 dx+I (n + 1)
π √ 0 (1 + x2 )
450 (using (1))
∞
2 √ I (n + 1)
Since e−x dx = π, = I (n) − 2n (I (n) − I (n + 1)) + I (n + 1)
−∞ √
∞
−x2 π
e dx = Hence proved.
0 2


2n − 1 3
As,I (n + 1) = I (n) I (2) = I(1),
2n 4
2n − 3 3 π
I (n) = I (n − 1) I (1) = · ,
2n − 2 4 2
2n − 5
I (n − 1) = I (n − 2)
2n − 4 2n − 3 2n − 5 2n − 7
2n − 7 Thus, I (n) = · · ···
I (n − 2) = I (n − 3) 2n − 2 2n − 4 2n − 6
2n − 6 1 3 2n − 3 π
and so on therefore, I (1) I (n) = · · · · ·
2 4 2n − 2 2

Ism et chapter_6

More Related Content

What's hot

Similar to Ism et chapter_6

More from Drradz Maths

Ism et chapter_6