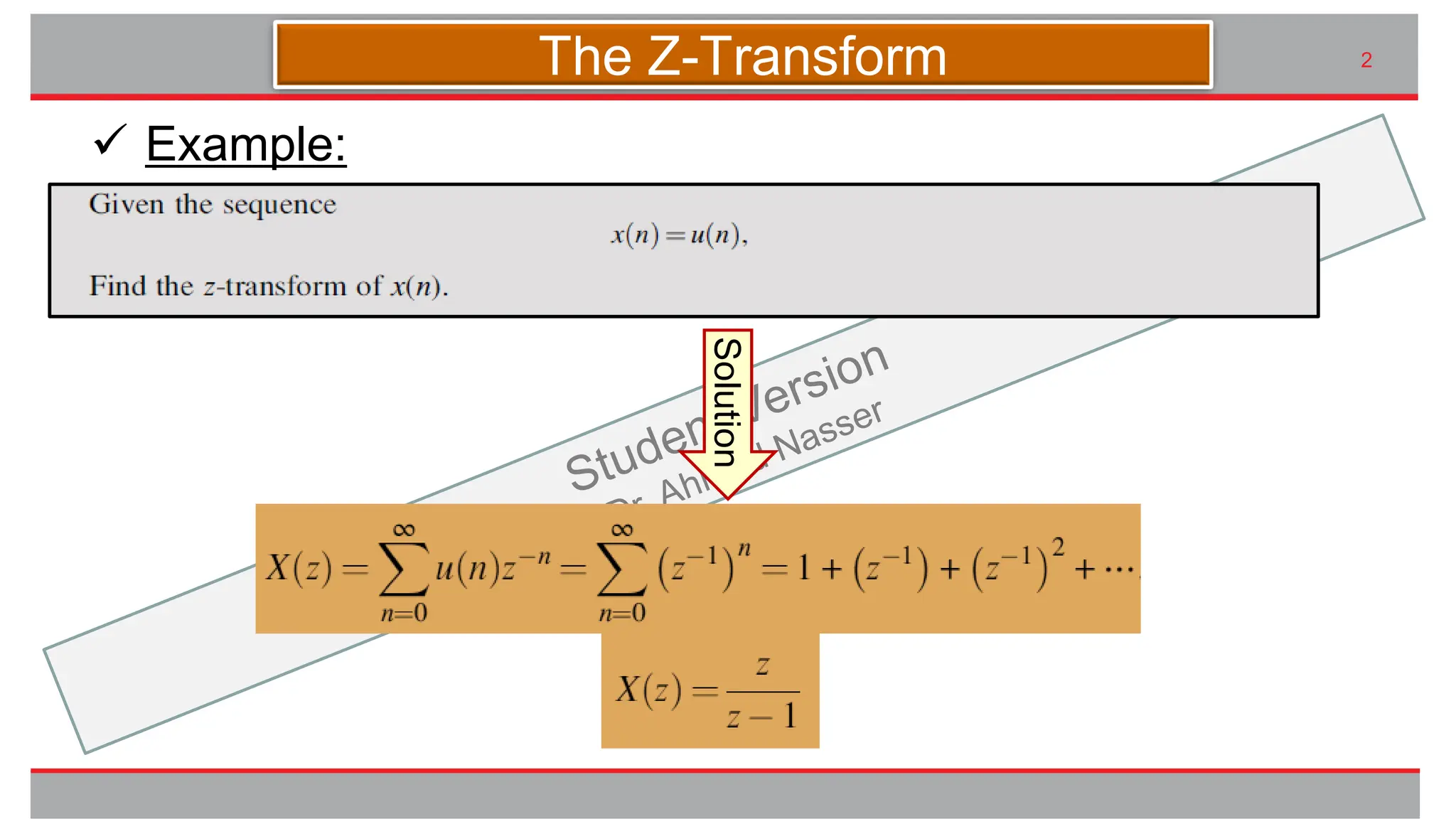
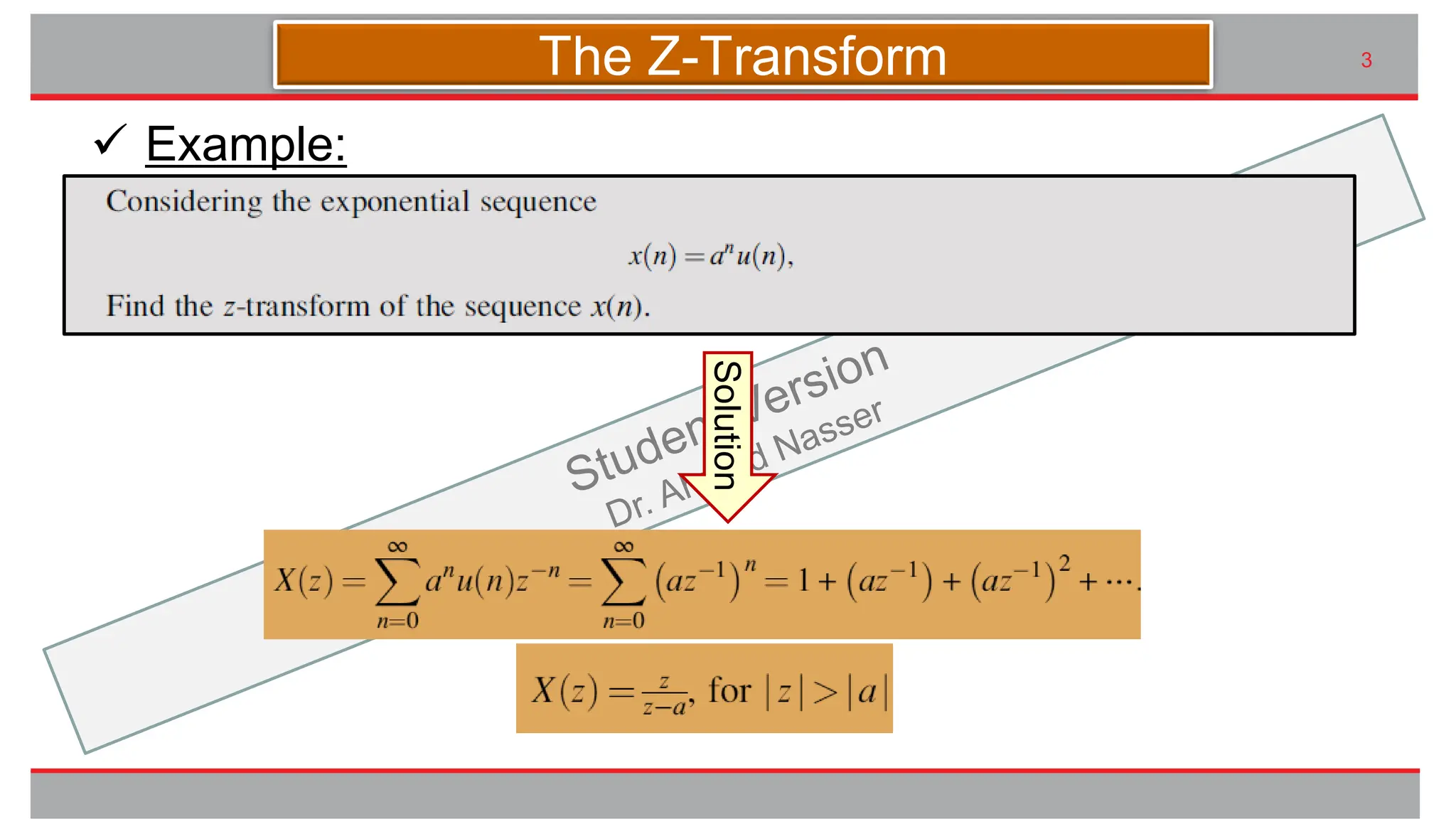
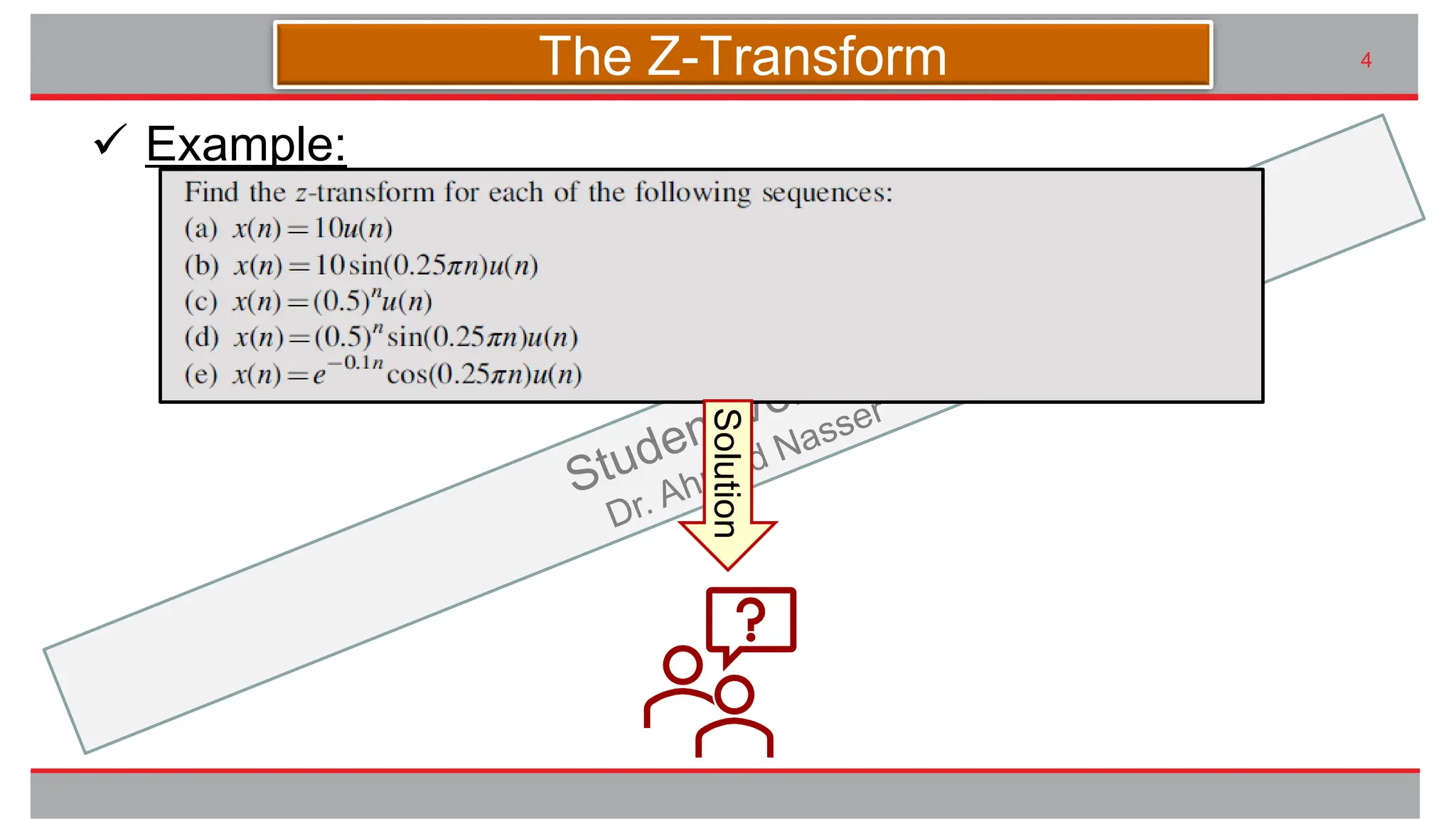
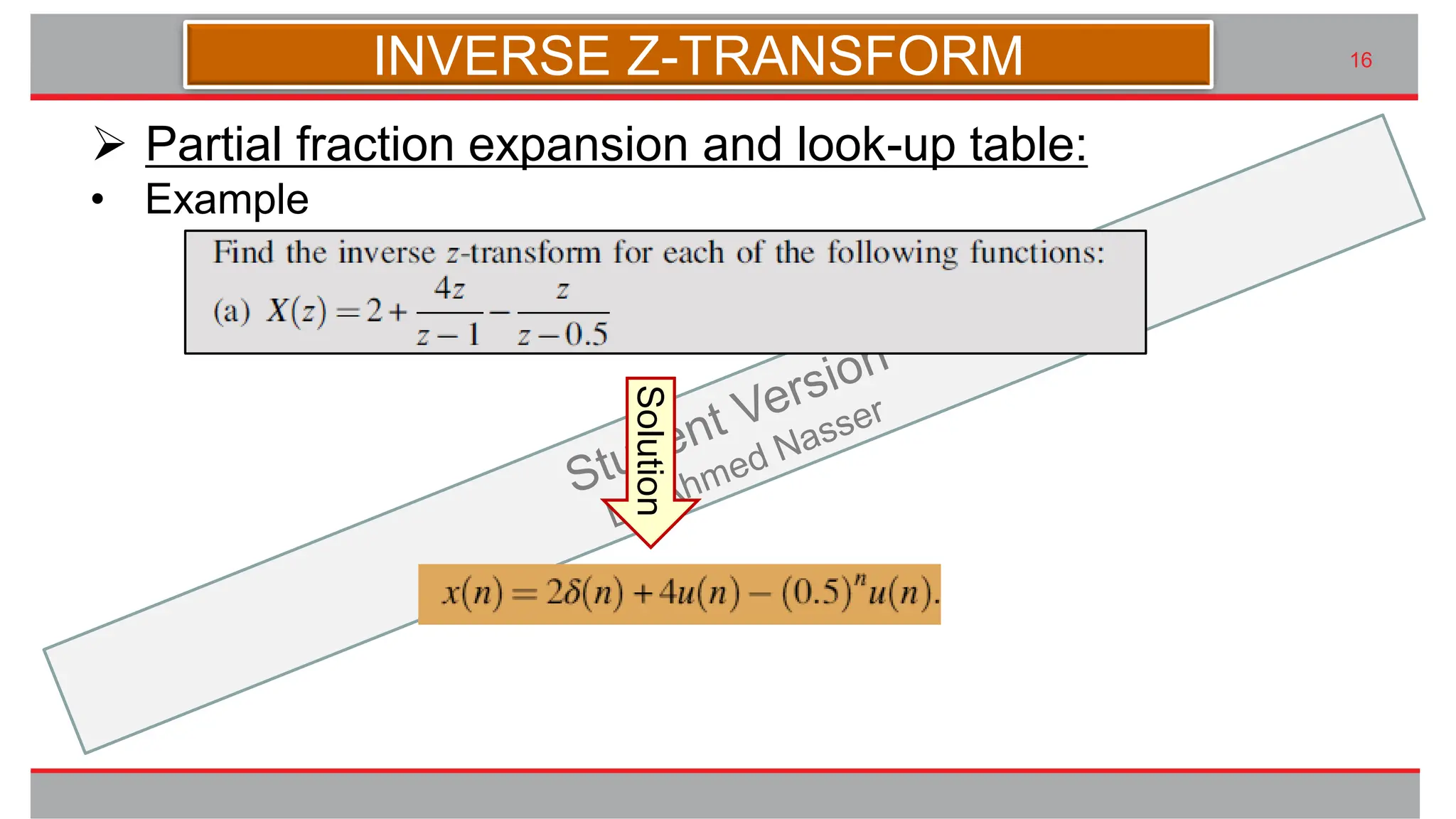
The document outlines the importance of the z-transform in analyzing digital systems, providing techniques for digital filter design and frequency analysis. It details the properties of the z-transform such as linearity, shift, convolution, as well as initial and final value theorems. Additionally, methods for obtaining the inverse z-transform are explained, including partial fraction expansion and look-up tables.