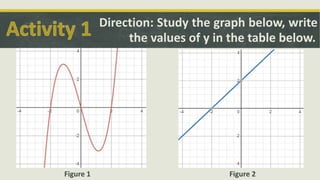
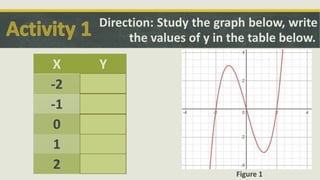
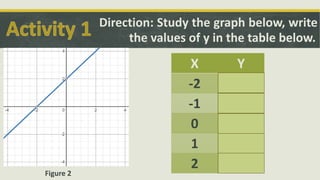
This document contains activities and lessons about functions, including: 1. Two activities that ask students to analyze graphs and tables to identify function properties like one-to-one and inverse functions. 2. A lesson explaining one-to-one functions, inverse functions, and how to determine if two functions are inverses. It provides examples of finding the inverse of different functions. 3. An activity that claims to be able to determine a number a student is thinking of through a series of math operations, linking it to the concept of inverse functions.

1. Activity 1

2. Direction: Study the graph below, write
the values of y in the table below.
Figure 1 Figure 2

3. Figure 1
X Y
-2 0
-1 3
0 0
1 -3
2 0
Direction: Study the graph below, write
the values of y in the table below.

4. Direction: Study the graph below, write
the values of y in the table below.
Figure 2
X Y
-2 0
-1 1
0 2
1 3
2 4

5. 1.What are the values of y in figure 1 and figure 2?
2.What have you noticed on their values?
3.Is the value of x in figure 1 have the same value in y? How
about figure 2?
4.Draw horizontal lines each figure. How many times does the
horizontal line intersect on figure 1 and figure 2?
5.What function do you call when no two ordered pairs that
have the same first component have different second
component?

6. Activity 2

7. Direction: Contact five (5) of your classmates to
write their Learner’s Reference Number
(LRN) on the table provided below.
Name of the
Student
LRN Questions:
1.What did you observe from the
table? Did you notice any repeated
LRN?
2.What do you think is the reason why
learners have their own LRNs?
3.What kind of function is depicted
from the given activity?

8. Activity 3

9. I Can See Your Mind!!!
Instructions:
1.Think of a number.
2.Multiply it by 2.
3.Then, subtract 1 from it.
4.Now, add 4 to the difference.
5.Lastly, give me your answer
and I’ll tell the number you
are thinking of.
Command Undo
Think of a number.
(x)
Answer
(x)
Multiply it by 2.
(2x)
Divide it by 2.
𝑦 − 4 + 1
2
Subtract 1 from it.
(2x-1)
Add 1 to it.
𝑦 − 4 + 1
Add 4 to the difference
(2x-1) + 4
Subtract 4 from it.
𝑦 − 4
Answer
(y)
Answer
(y)

10. One-to-One and Inverse
Functions

11. Objectives
 Define and identify one-to-one and
inverse functions;
 Determine the inverse of a given
function;
 Show that two functions are inverses.

12. One-to-One function
A function f is one-to-one if it never
takes the same value twice or 𝑓 𝑥1 ≠
𝑓 𝑥2 whenever 𝑥1 ≠ 𝑥2 . That is,
the same y-value is never paired with
two different x-values.

13. Reminder:
 When working on the coordinate
plane, a function is a one-to-one
function when it will pass the vertical
line test (to make it a function) and also
a horizontal line test (to make it one-to-
one).

14. Inverse Function
Let f be a one-to-one function with
domain A and range B. Then the inverse of
f, denoted by 𝑓−1
, is a function with
domain B and range A defined by
𝑓−1
𝑦 = 𝑥 if and only if f(x) = y for any y
in B.

15. Showing that Two Functions are
Inverses
Two functions f(x) and g(x) are inverse functions if and only if:
1. For each x in the domain of g, g(x) is in the domain of f and
𝒇 °𝒈 𝒙 = 𝒇 𝒈 𝒙 = 𝒙
2. For each x in the domain of f, f(x) is in the domain of g and
𝒈 ° 𝒇 𝒙 = 𝒈 𝒇 𝒙 = 𝒙

16. Finding the Inverse of a Function
To find the inverse of a function, follow these steps.
1.Write f(x) as y.
2.Interchange x and y.
3.Solve for y in terms of x.
4.The resulting function is 𝒇−𝟏
𝒙 .

17. Example 1
𝑓 𝑥 = 4𝑥 − 5

18. Example 2
𝑓 𝑥 =
𝑥5
+ 4
3

19. Example 3
𝑓 𝑥 = 4 − 𝑥2
, 𝑥 ≥ 0

20. Example 4
𝑓 𝑥 =
2𝑥 + 1
3𝑥 − 4

21. Example 5
𝑓 𝑥 =
𝑥 − 4
2
2

22. Assessment 1
𝑓 𝑥 = 𝑥 − 2

23. Assessment 2
𝑓 𝑥 = 3 𝑥 − 3