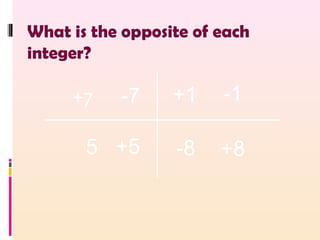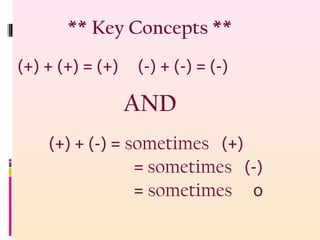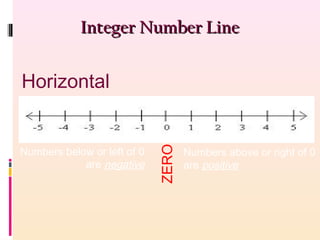
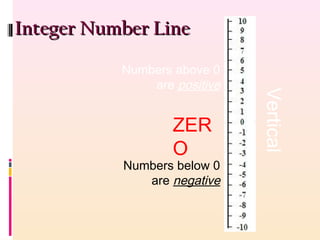
The document provides an introduction to integers including: - Definitions of positive and negative numbers and their representation on number lines - Rules for comparing and ordering integers - Real-world examples of how integers are used to represent things like temperature, sea level, and money - Key concepts and rules for adding and subtracting integers including keeping the sign of the first integer the same and changing the operation and second integer's sign for subtraction - Examples of using number lines to visually represent integer operations - A method for proving that subtracting a negative number is the same as adding a positive number

1. INTERESTINGINTERESTING
INTEGERS!INTEGERS!
5
-7
-3
-8
4

2. What You Will Learn:What You Will Learn:
 Vocabulary related to integers
 Rules for adding and subtracting
integers
 A method for proving that a rule is true
Are you ready??Are you ready??

3. Part I: Introduction to IntegersPart I: Introduction to Integers
•VocabularyVocabulary
• positive numberpositive number
• negative numbernegative number
•Horizontal & vertical number linesHorizontal & vertical number lines
•Comparing IntegersComparing Integers
•Ordering IntegersOrdering Integers
•Vocabulary - continuedVocabulary - continued
• opposite numberopposite number
• integerinteger
•Real World Applications & ExamplesReal World Applications & Examples
• temperaturetemperature
• sea levelsea level
• moneymoney

4.  Positive number – a number
greater than (>) zero
0 1 2 3 4 5 6
Vocabulary:

5. Hint:Hint:
 If you don’t see a negative or
positive sign in front of a number,
the number is positive.
9 is the same as +9

6.  Negative number – a number less
than (<) zero
0 1 2 3 4 5 6-1-1-2-2-3-3-4-4-5-5-6-6
Vocabulary:

7. Integer Number LineInteger Number Line
Horizontal
Numbers above or right of 0
are positive
Numbers below or left of 0
are negative ZERO

8. Integer Number LineInteger Number Line
Vertical
Numbers above 0
are positive
ZER
O
Numbers below 0
are negative

9. Use the number line to compare the
following integers with >, <, or =.
-4 -2 1 -3 -5 0
Hint: On a number line, the number to the left is
always less than the number to the right.
Comparing IntegersComparing Integers
<
< >

10. Use the number line to compare
the following integers with >, <,
or =.
Comparing IntegersComparing Integers
Hint: On a number line, the number on the
top is always greater than the number on
the bottom.
-3 -5 -5 0 0 -1>
>
>

11. Ordering IntegersOrdering Integers
Use the number line to put the following
integers in order from least to greatest.
-4, 3, 0, and -5 -5, -4, 0, 3

12.  Opposite Numbers – numbers
that are the same distance from
zero in the opposite direction
0 1 2 3 4 5 6-1-2-3-4-5-6
Vocabulary:

13. What is the opposite of each
integer?
+7 -7
+5
-1
+8
+1
5 -8

14. Vocabulary:
Integers – all the whole numbers
and all of their opposites on the
number line including zero
0 1 2 3 4 5 6-1-2-3-4-5-6
integers

15. Now, you’re probably saying,
“That’s interesting and
everything, BUT where are
negative numbers in the real
world??
??

16. Negative Numbers Are Used to
Measure Temperature

17. Negative Numbers Are Used to
Measure Under Sea Level
0
10
20
30
-10
-20
-30
-40
-50

18. Positive and negative numbers
are used when keeping track of
money.
+ Positive +
$$ you earn
- Negative -
$$ you spend

19. Positive Numbers are Used to Show
Earnings or Assets
When you get paid
(or win the lottery),
you add that $$ to
your account.

20. Negative Numbers are Used to Show
What You Owe or Debt
If your mom loaned you $10 for pizza,
Mom,
I. O. U.
$10
The $10 you owe her is described by
the integer -10.

21. Write an integer to describe the real
world situation:
 Gain 3 pounds:
 Withdraw $15:
 5 feet below sea level:
 Move ahead 4 spaces:
3 or +3
-15
-5
4 or +4

22. End - Part I: Introduction to IntegersEnd - Part I: Introduction to Integers
•VocabularyVocabulary
• positive numberpositive number
• negative numbernegative number
•Horizontal & vertical number linesHorizontal & vertical number lines
•Comparing IntegersComparing Integers
•Ordering IntegersOrdering Integers
•Vocabulary - continuedVocabulary - continued
• opposite numberopposite number
• integerinteger
•Real World Applications & ExamplesReal World Applications & Examples
• temperaturetemperature
• sea levelsea level
• moneymoney

23. Part II: Adding IntegersPart II: Adding Integers
Key ConceptsKey Concepts
Integer Addition RulesInteger Addition Rules
Using Number LinesUsing Number Lines

24. ** Key Concepts **** Key Concepts **
The sum of two positive numbers is always
positive  (+) + (+) = (+)
ex. 5 + 1 = 6
The sum of two negative numbers is always
negative  (-) + (-) = (-)
ex. -5 + -1 = -6

25. ** Key Concepts **
(+) + (+) = (+) (-) + (-) = (-)
(+) + (-) = sometimes (+)
= sometimes (-)
= sometimes 0
AND

26. Integer Addition RulesInteger Addition Rules
 Rule #1 – If the signs are the same, add
the numbers and then put the sign of the
addends in front of your answer.
b) -9 + -5 = -14
a) -9 + -5 =

27. SolveSolve the Problemsthe Problems
 -3 + -5 =
 4 + 6 =
 +3 + (+4) =
 -6 + -7 =
 5 + 9 =
 -9 + -9 =
-8
-18
14
-13
7
10

28.  Rule #2 – If the signs of the addends are
DIFFERENT, start at the location of the
first integer on the number line and:
 a) move RIGHT to add a positive integer
Integer Addition RulesInteger Addition Rules
-5 + 3 = -2
1 2 3

29. ex. (-6) + 5 = -1Start here at -6
0 1 2 3 4 5 6-1-2-3-4-5-6
then count forward or right 5 spaces
+
Adding Integers Using a Number LineAdding Integers Using a Number Line
* adding a* adding a positive integer *integer *

30. Solve the ProblemsSolve the Problems
• 8 + 6 =
• (-9) + 5 =
• (–11) + 11 =
• (–8) + 16 =
14
0
8
-4

31.  Rule #2 – If the signs of the addends are
DIFFERENT, start at the location of the
first integer on the number line and:
 b) move LEFT to add a negative integer
Integer Addition RulesInteger Addition Rules
4 + -3 = 1
123

32. 0 1 2 3 4 5 6-1-2-3-4-5-6
-
ex. +3 + (-5) = -2
Start here at +3
Then count back or left 5 spaces
Adding Integers Using a Number LineAdding Integers Using a Number Line
* adding a* adding a negative integer *integer *

33. Solve the ProblemsSolve the Problems
• 2 + (-12) =
• –8 + (-5) =
• 14 + (-7) =
• 15 + (-15) =
-10
7
-13
0

34. Part III

35. Part III: Subtracting IntegersPart III: Subtracting Integers
** Key Concept **** Key Concept **
To subtract an integer, add its opposite
ex. 5 – 2 = 5 + (-2) = 3
KEEP
CHANGE
CHANGE

36. ex. -1 – (-2) is the same as
-1 + (+2) and -1 + 2 = 1
Subtracting a negative number is
the same as adding a positive.
Change the signs and add.
Integer Subtraction Rule
KEEP
CHANGE
CHANGE

37. -3 – 4 is the same as
-3 + (-4) and -3 + (-4) = -7
More Examples
2 – (-7) is the same as
2 + (+7) and 2 + 7 = 9
KEEP the sign of the 1st
integer the same
CHANGE the operation ( + to – or – to +)
CHANGE the sign of the 2nd
integer

38. More Examples
12 – (-8) is the same as
12 + (+8) and 12 + 8 = 20
-3 – (-11) is the same as
-3 + (+11) and -3 + 11 = 8
KEEP the sign of the 1st
integer the same
CHANGE the operation ( + to – or – to +)
CHANGE the sign of the 2nd
integer

39. Problems
to Solve
8 – (-12) is the same as
8 + (+12) and 8 + 12 = 20
22 – (-30) is the same as
22 + (+30) and 22 + 30 = 52
KEEP the sign of the 1st
integer the same
CHANGE the operation ( + to – or – to +)
CHANGE the sign of the 2nd
integer

40. Problems to Solve
-17– (-3) is the same as
-17 + (+3) and -17 + 3 = -14
-8 – 3 is the same as
-8 + (-3) and -8 + -3 = -11
KEEP the sign of the 1st
integer the same
CHANGE the operation ( + to – or – to +)
CHANGE the sign of the 2nd
integer

41. Part IV

42. How do we know that
“Subtracting a negative number is the
same as adding a positive” is true?
We can use the same method we
use to check our answers when we
do regular subtraction.

43. When you subtract a – b it equals c
a – b = c
ex. 5 – 2 = 3
To check if your answer is correct,
add b and c
a = b + c
ex. 5 = 2 + 3

44. If a – b = c, and….
2 – (-5) is the same as
2 + (+5), which equals 7,
Then let’s check with the
negative numbers to see if it’s
true…

45. Here are some examples:
a – b = c a = b + c
9 – 5 = 4 9 = 5 + 4
a – b = c a = b + c
20 – 3 = 17 20 = 3 + 17

46. If the method for checking
subtraction works, it should
also work for subtracting
negative numbers.

47. a – b = c a = b + c
2 – (-5) = 7 2 = -5 + 7
It works!
a – b = c a = b + c
-11 – (-3) = -8 -11 = -3 + -8
YES!

48. Aren’t integers
interesting?