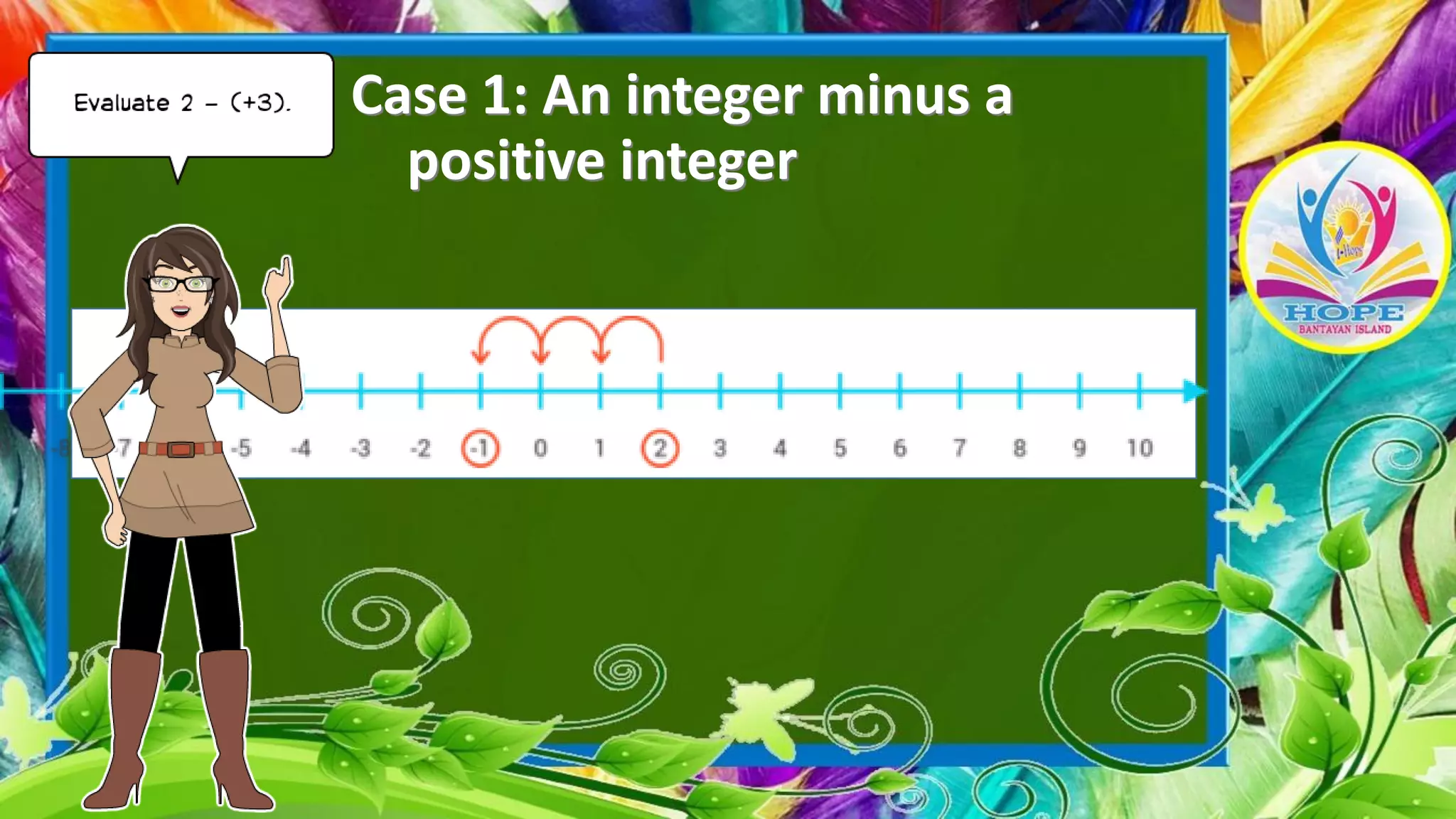
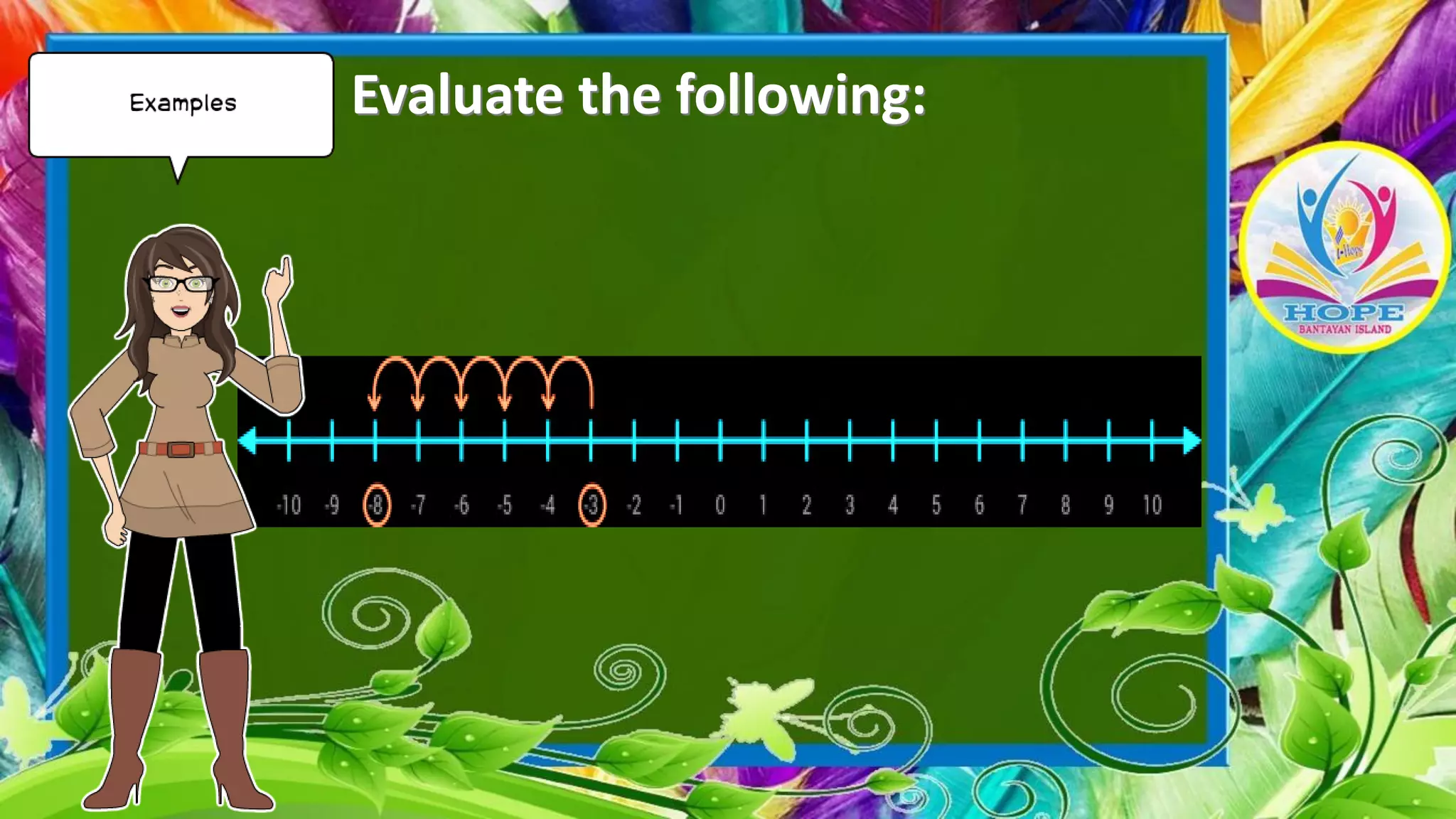
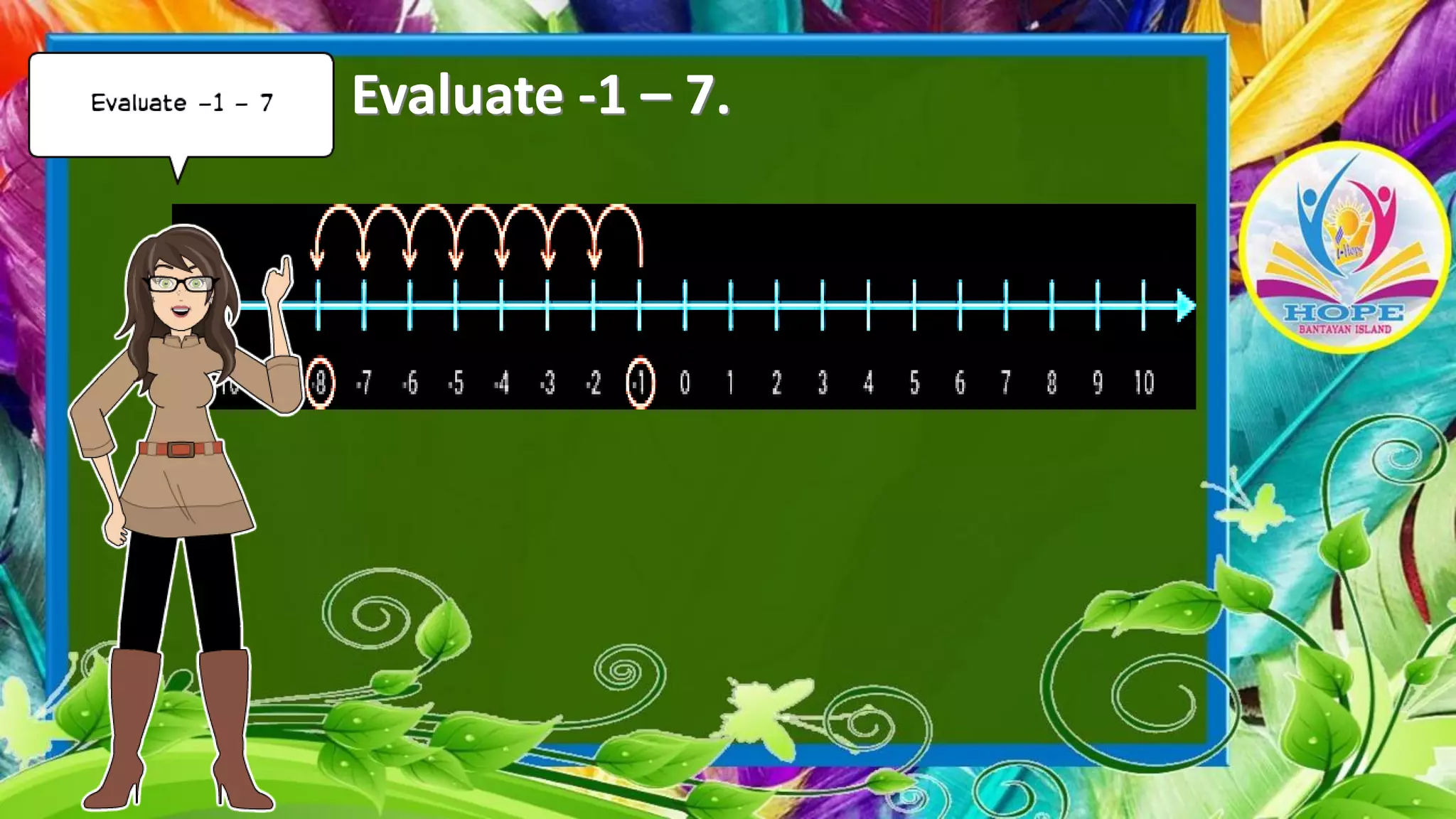
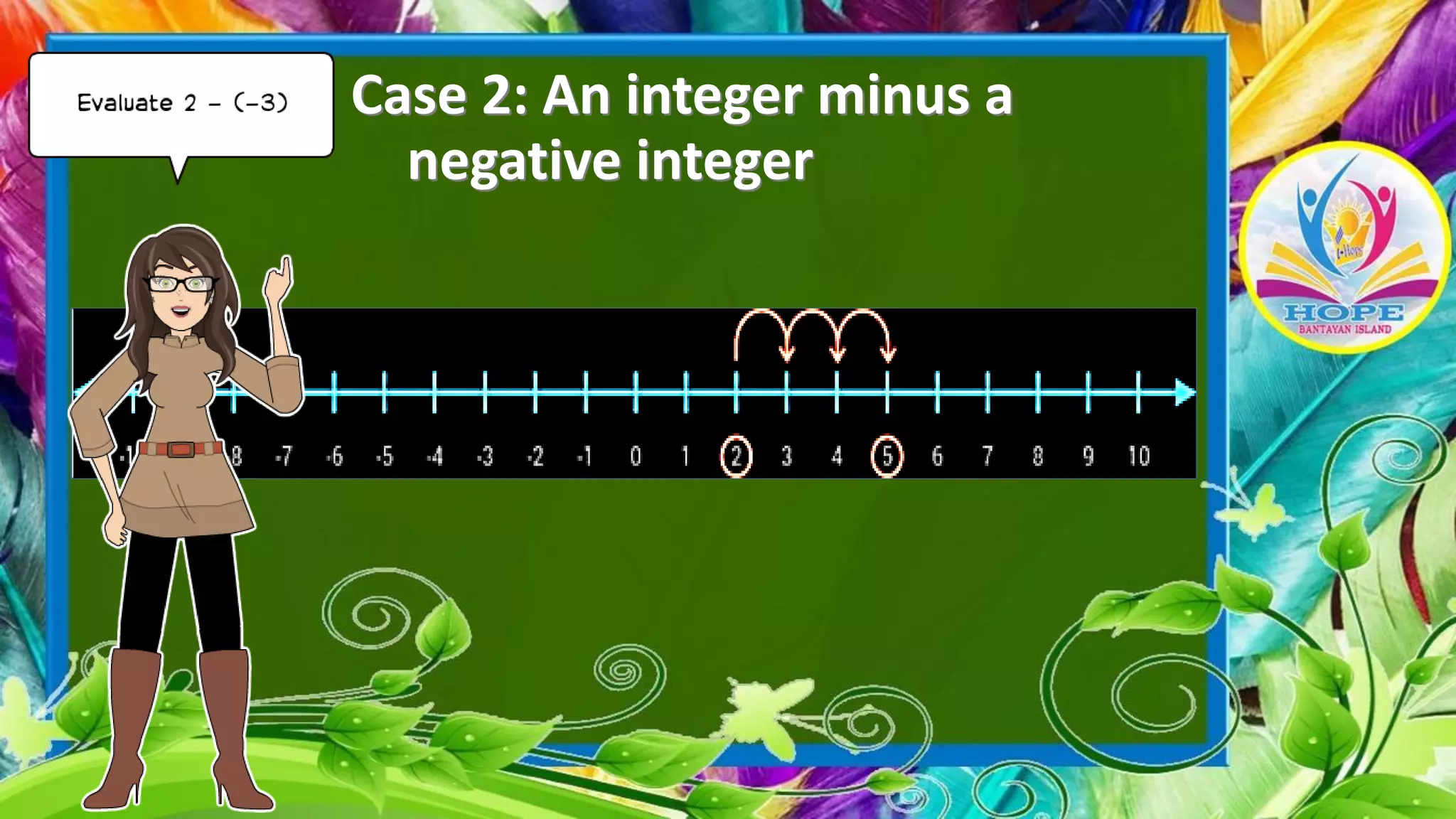
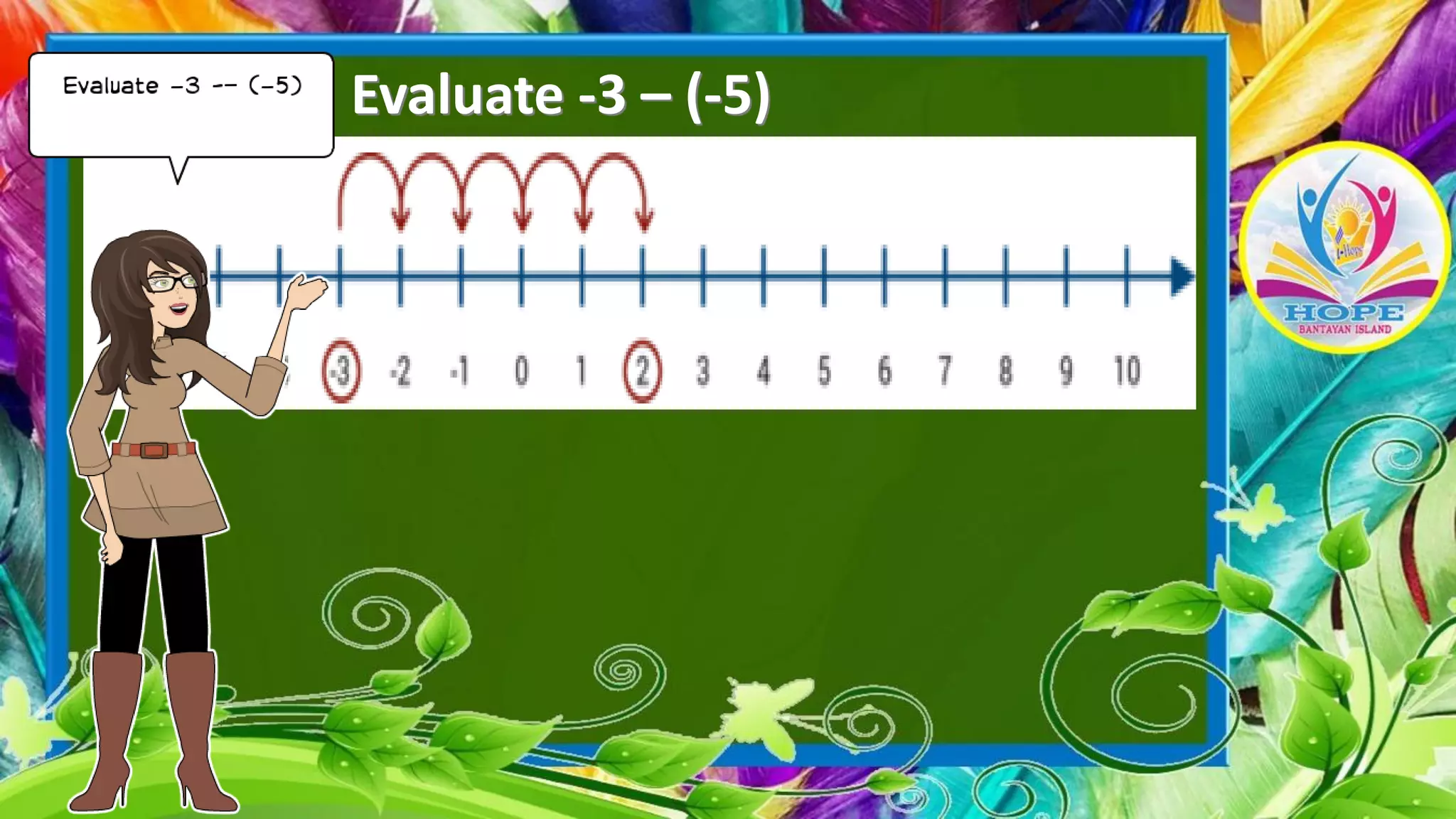
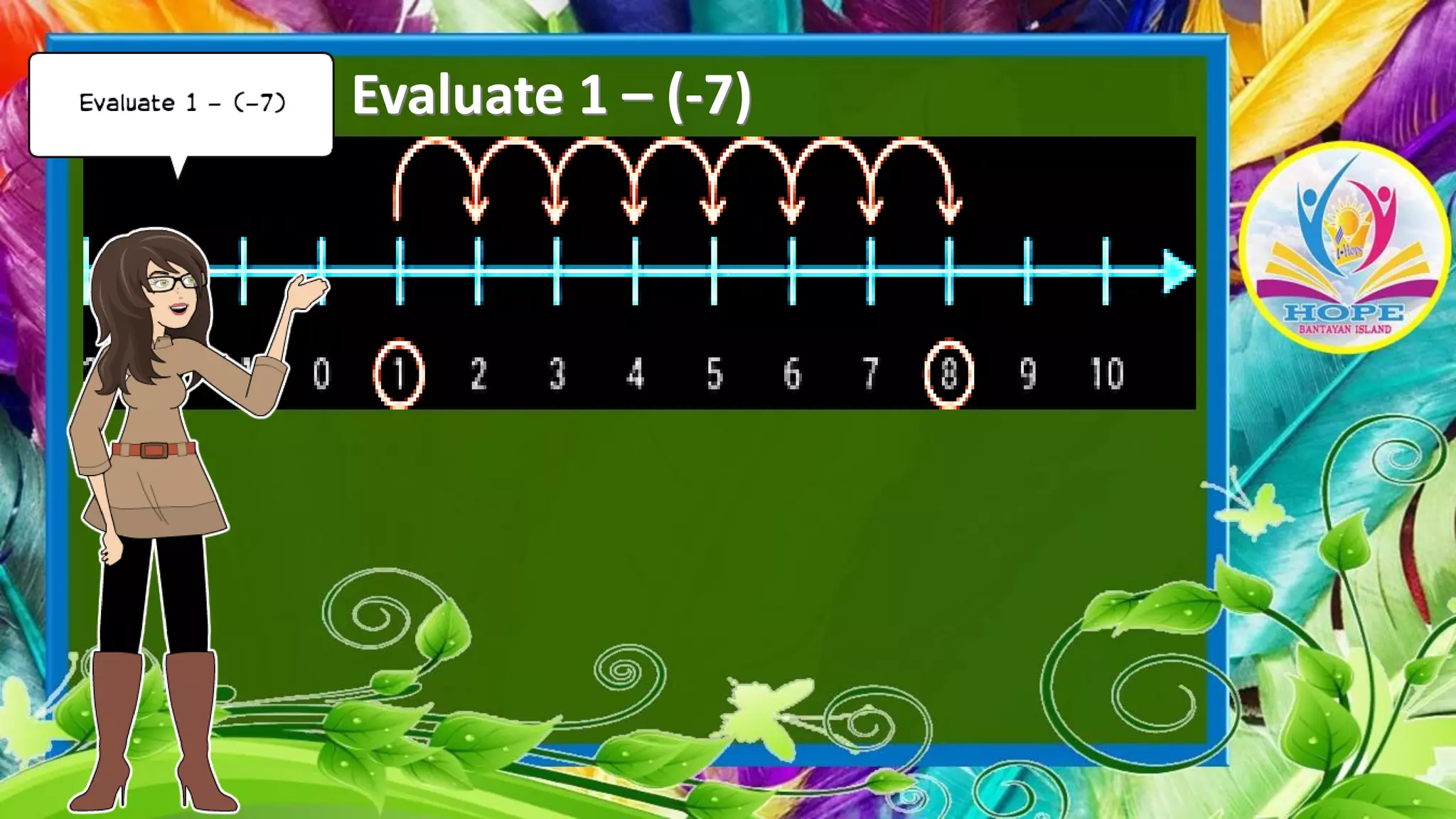
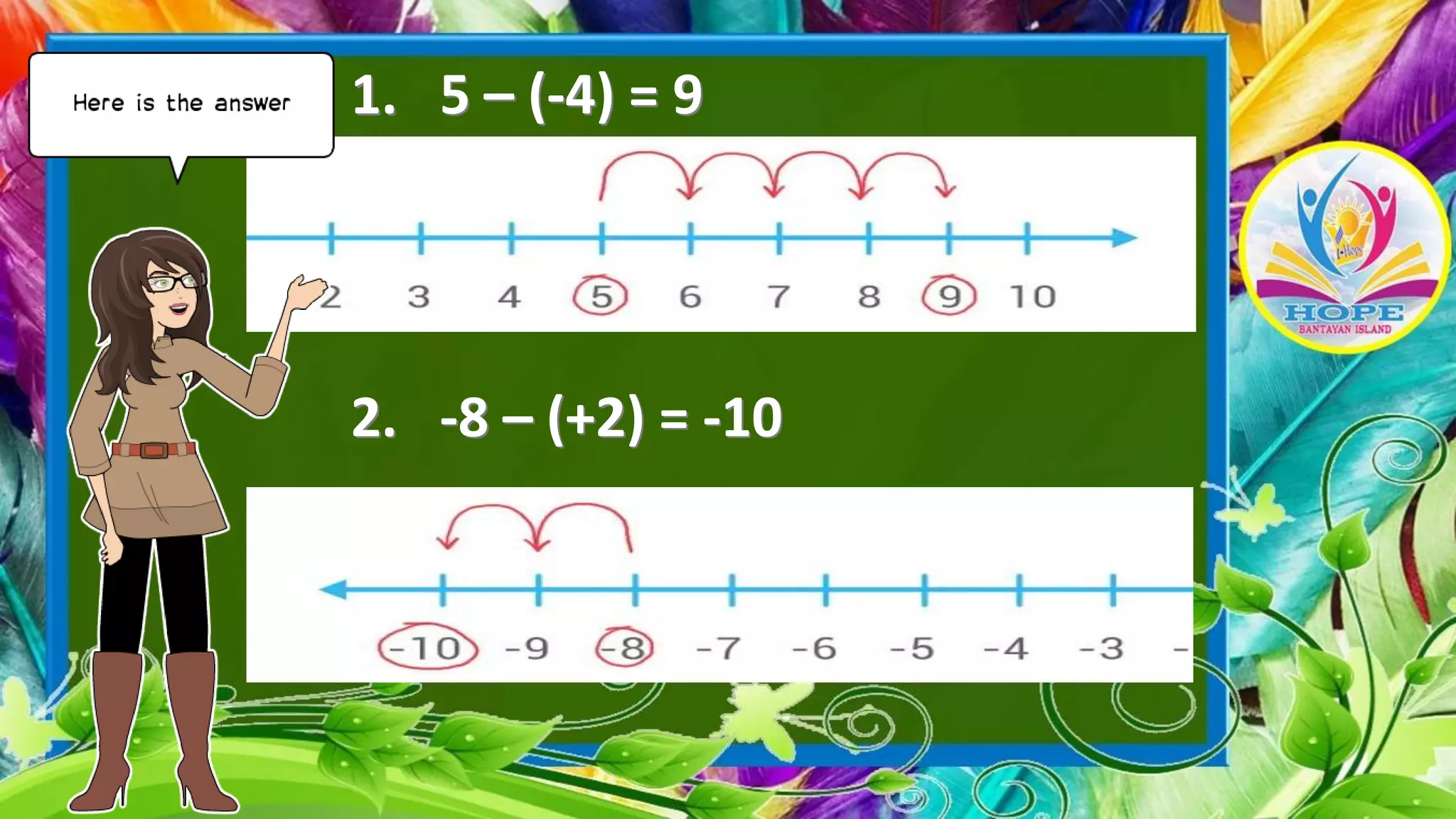
The document discusses subtracting integers using a number line. It explains that subtracting a positive integer moves left, while subtracting a negative integer moves right. It provides examples of subtracting integers with both positive and negative numbers, demonstrating how to evaluate the expressions on a number line by starting at the first integer and moving the indicated number of units in the appropriate direction.

2. The subtraction of integers involves two
cases. In this lesson, we will discuss each
case using the number line.
Recall that a positive sign indicates
movement to the right of the number
line. On the other hand, a negative sign
indicates movement to the left of the
number line.

3. Case 1: An integer minus a
positive integer

4. Case 1: An integer minus a positive
integer
We begin at 2 on the number line,
then move 3 units to the left.
The final position is -1. We
moved to the opposite direction
because of the negative sign.
Note: A positive sign in means to
continue in the same direction
(to the left).

6. Evaluate the following:

7. We begin at -3 on the number
line. The subtraction sign tells
us that we should move 5
units to the left on the number
line. We will not change
direction because the sign on
5 is positive.
So, we start at -3, move 5 units
to the left, and stop at .
Thus, -3 – (+5) = -8

8. Evaluate -1 – 7.

9. Most of the time, subtraction
problems are written without
parentheses (and positive
signs). This problem is the
simplified form of -1 – (+7).

10. We begin at -1 on the number line.
Then, because of the negative
sign, we change directions and
move left. The number 7 tells us
that we should move 7 units to
the left.
So we start at -1, move 7 units to
the left, and stop at -8.
Thus, -1 – 7 = -8.

11. Case 2: An integer minus a
negative integer

12. We begin at the point 2 on the
number line and wish to move to
the negative direction (to the
left) because of the first negative
sign. However, the second
negative on -3 tells us to move in
the opposite direction again.
Thus, instead of moving to the
left, we move in the opposite
direction (to the right).

13. So, we start at 2, move 3 units to
the right, and stop at 5.
Thus, 2 – (-3) = 5.

14. Evaluate the following:
1. -3 – (-5)
2. 1 – (-7)

15. Evaluate -3 – (-5)

16. We begin at -3 on the number
line. The first negative sign
tells us to move to the left.
The second negative sign on -5
tells us to change direction
again (to the right). The
number 5 tells us how many
units to move.

17. So we start at -3, move 5 units to
the right, and stop at 2.
Thus, -3 – (-5) = 2

18. Evaluate 1 – (-7)

19. We begin at 1 on the number
line. The first negative sign
tells us to move to the left.
The second negative sign on -7
tells us to change direction
again (to the right). The
number 7 tells us how many
units to move.

20. So we start at 1, move 7 units to
the right, and stop at 8.
Thus, 1 – (-7) = 8.

21. Evaluate the following:
1. 5 – (-4)
2. -8 – (+2)

22. 1. 5 – (-4) = 9
2. -8 – (+2) = -10

23. Evaluate -2 – (-14) – 5.

24. A negative sign is a prompt to
move a certain number of units
in the opposite direction on the
number line.
We move to the left when
subtracting a positive integer. On
the other hand, we move to the
right when subtracting a
negative integer.

25. Which of the following best
describes the solution to 3 – (-5) on
the number line?
a. Start at point 3 and move 5 units
to the right.
b. Start at point 5 and move 3 units
to the left.
c. Start at point 3 and move 5 units
to the left.
d. Start at point 5 and move 3 units
to the right.

26. Which of the following best
describes the solution to 10 – (+12)
on the number line?
a. Start at point 12 and move 10
units to the right.
b. Start at point 12 and move 10
units to the left.
c. Start at point 10 and move 12
units to the left.
d. Start at point 10 and move 12
units to the right.

27. Simplify -10 – (+3).
a. -13
b. 13
c. -7
d. 7

28. Simplify 8 – (+2).
a. 6
b. -6
c. -10
d. 10

29. Simplify 5 – (-7).
a. 2
b. -12
c. -2
d. 12

30. Simplify -7 – (+2).
a. -5
b. 5
c. 9
d. -9

31. Simplify 2300 – (-300).
a. -2600
b. 2000
c. 2600
d. -2000

32. Simplify -24 – (-13) – (-24).
a. 61
b. -13
c. -61
d. 13

33. An equation is true when
both sides can be simplified
to the same value. Which of
the following equations are
true?
a. 4 – 5 = 4 – (+5)
b. -8 – (-6) = -8 - 6
c. -3 – (-2) = -3 + 2
d. 4 – (-2) = 4 – (-2)