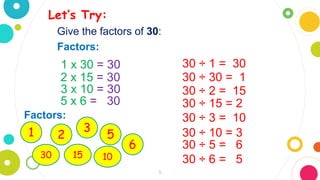
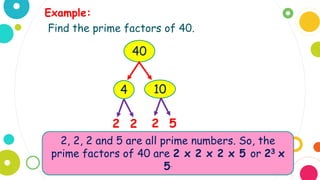
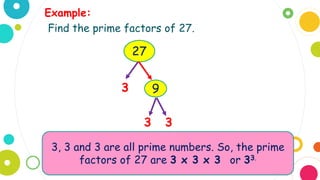
The document explains what factors and prime factorization are. It provides examples of finding the factors of numbers like 30, 26, 15, 22, 34, and 25. It then defines prime factorization as finding the prime factors of a number. Two methods for prime factorization are described: the factor tree method and the continuous division method. Examples are given of using these methods to find the prime factors of 40 and 27.

2. 2

3. Factors of a
Number
3

4. 4
Factors – are the numbers
multiplied to get a product.
• Numbers which divide a number
with no remainder are called
factors of the number.
Remember:

5. 5
Let’s Try:
Give the factors of 30:
Factors:
1 x 30 = 30
2 x 15 = 30
1
30
2
15
Factors:
30 ÷ 1 = 30
30 ÷ 30 = 1
30 ÷ 2 = 15
30 ÷ 15 = 2
3 x 10 = 30
5 x 6 = 30
3
10
5
6
30 ÷ 3 = 10
30 ÷ 10 = 3
30 ÷ 5 = 6
30 ÷ 6 = 5

6. 6
Let’s Try:
Give the factors of 26:
Factors:
1 x 26 = 26
2 x 13 = 26
1 26 2 13
Factors:
26 ÷1 = 26
26 ÷ 26 = 1
26 ÷ 2 = 13
26 ÷ 13 = 2

7. 7
Let’s Try:
Give the factors of the following. Write it in your
notebook:
1.) 15
2.) 22
= 1, 15, 3, 5
3.) 34
4.) 25
= 1, 22, 2, 11
= 1, 34, 2, 17
= 1, 25, 5

8. Prime
Factorization
8

9. 9
Prime Factorization – is finding the
prime factors of a number.
• The two methods used in prime
factorization are the factor tree
and the continuous division.
Remember:

10. 10
Factor Tree Method
1.Think of any factors of the given
number.
2.If the two factors are not yet
prime, write each of them as the
product of any 2 factors again, Keep
going until you have only prime
numbers.

11. 11
Example:
Find the prime factors of 40.
40
4 10
2 2 2 5
2, 2, 2 and 5 are all prime numbers. So, the
prime factors of 40 are 2 x 2 x 2 x 5 or 23 x
5.

12. 12
Example:
Find the prime factors of 27.
27
9
3
3 3
3, 3 and 3 are all prime numbers. So, the prime
factors of 27 are 3 x 3 x 3 or 33.

13. 13
Continuous Division Method
1.Think of the smallest prime factor
of the given number as the divisor.
2.Continue dividing by a prime factor
until the divisor is the same as the
dividend..

14. 14
Example:
Find the prime factors of 40.
2, 2, 2 and 5 are all prime numbers. So, the
prime factors of 40 are 2 x 2 x 2 x 5 or 23 x
5.
40
2
20
2
10
2
5
5
1

15. 15
Example:
Find the prime factors of 27.
27
3
9
3
3
3
1
3, 3 and 3 are all prime numbers. So, the prime
factors of 27 are 3 x 3 x 3 or 33.

16. 16
1. Answer page 31.

17. 17
1. Answer page 32-33 (10-18)

18. 18

19. 19
All for Thee, my
Jesus
All for Thee, Amen.

20. 20