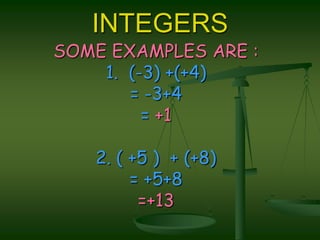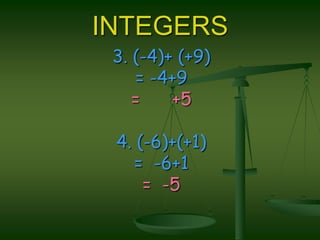Integers are the collection of whole numbers and their negatives. There are two types of integers: positive integers like 1, 2, 3, etc. and negative integers like -1, -2, -3, etc. Integers are ordered on the number line, with positive integers to the right of zero and negative integers to the left. Addition and subtraction of integers follows sign rules - integers with the same sign are added/subtracted normally, and integers with different signs are subtracted but keep the sign of the larger integer. Integers are used in daily calculations like balances that can be positive or negative. Multiplication and division of integers also follows consistent sign rules.

1. BY AAKANKSHAVI - DINTEGERS

2. INTEGERSQ1. What are integers ? A1. The First numbers to be discovered were natural numbers i.e.1, 2,3,4,… After including Zero to them we get whole numbers. But there are negative numbers too. If we put whole numbers and negative together, the new collection is called Integers.

3. INTEGERSTYPES OF INTEGERS 1. Positive Integers- The positive numbers are called positive Integers e.g. 1,2,3,4,…2. Negative Integers-The negative numbers are called Negative Integers e.g. -1,-2,-3,-4,….

4. INTEGERSORDERING OF INTEGERSThe numbers on the right side of zero on number line will be the bigger one, i.e. 0<1<2<3<4,….The numbers on the left side of Zero on Number line will be smaller one, i.e. 0>-1>-2>-3>-4,…..

5. INTEGERSADDITION AND SUBTRACTION WITH THE SAME SIGNWe add the two positive Integers like(+3)+(+2) = +5 [=3+2]We also add when we have two negative Integers but the answer will take a minus (-) sign like (-2) +(-1)= -(2+1)= -3

6. INTEGERSADDITION OF INTEGERS OF DIFFERENT SIGNWhen we have one positive and one negative integer, we must subtract , but the answer will take the sign of the bigger integer. ( Ignoring the sign of the numbers decide which is bigger)Example:- (+5) + (-8) = (5-8) = -3 (+6) + (- 4) = ( 6 – 4) = +2

7. INTEGERSUSES OF INTEGERS IN DAILY LIFEEvery day in our daily life we use the integers for calculations . The figures are taken in positive and negative terms and it becomes possible to do the calculations. This can be understood by the following examples.

8. INTEGERSSOME EXAMPLES ARE :1. (-3) +(+4)= -3+4= +12. ( +5 ) + (+8)= +5+8=+13

9. INTEGERS3. (-4)+ (+9)= -4+9= +54. (-6)+(+1)= -6+1= -5

10. INTEGERSRULES FOR MULTIPLICATION(-) x (+) = (-) (-) x ( -) = ( +) (+ ) x ( +) = ( +) (+ ) x ( - ) = ( - )FROM THE ABOVE RULES IT IS CLEAR THAT REMEMBERING THE SIGN RULES IS VERY IMPORTANT IN SOLVING INTEGERS PROBLEMS OF MULTILICATION.

11. INTEGERSRULES FOR DIVISION( -) / ( + ) = ( - )( -) / ( - ) = ( + )( + ) / ( + ) = ( + )(+ ) / ( - ) = ( -) AS MULTIPLICATION IN CASE OF DIVISION ALSO THE SIGN RULES ARE VERY IMPORTANT. THE NEGATIVE AND POSITIVE NUMBERS WILL BE VALUED AS PER THE ABOVE RULES.