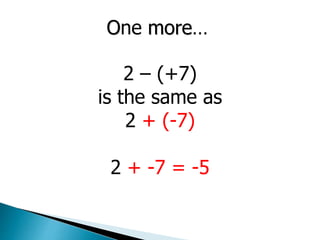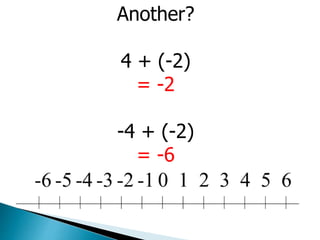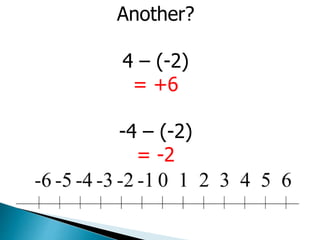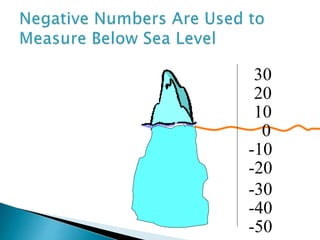
The document defines integers and provides rules for adding and subtracting integers: - Integers include all positive whole numbers and their opposites, including zero. - For addition, if signs are the same, add the numbers and keep the sign; if different, subtract the smaller number from the larger and keep the sign of the number with the larger absolute value. - For subtraction, change a negative number to its positive equivalent by changing the sign, then add. This allows subtraction to follow the same rules as addition.

2.  Some definitions related to integers.
 Rules for adding and subtracting integers.
 Different methods that will work for you.
Are you ready??
 Add with negative integers
 Subtract positive integers from negative integers

3. Positive number – a
number greater than zero.
0 1 2 3 4 5 6

4. Negative number – a
number less than zero.
0 1 2 3 4 5 6-1-2-3-4-5-6

5.  Opposite Numbers – numbers
that are the same distance
from zero in the opposite
direction
0 1 2 3 4 5 6-1-2-3-4-5-6

6.  Integers – Integers are all the
positive whole numbers and
all of their opposites,
including zero.
7 opposite -7

7.  Absolute Value – It is the
distance a number is from zero
on the number line.
The absolute value of
+9 or of –9 is 9.

9. 0
10
20
30
-10
-20
-30
-40
-50

10. If you don’t see a
negative or positive sign
in front of a number it is
positive.
9+

11.  Rule #1 – If the signs are the same,
pretend the signs aren’t there.
Add the numbers and then put the
sign of the addends in front of
your answer.
9 + 5 = 14
-9 + -5 = -14

12.  Rule #2 – If the signs are different
pretend the signs aren’t there.
Subtract the smaller from the larger
one and put the sign of the one with
the larger absolute value in front of
your answer.
-9 + +5 =
9 - 5 = 4
Larger abs. value
Answer = - 4

13. Integer Subtraction Rule
Subtracting a negative number is the
same as adding a positive. Change
the signs and add.
2 – (-7)
is the same as
2 + (+7)
2 + 7 = 9

14. -2 – (+7)
is the same as
-2 + (-7)
-2 + -7 = -9
Let’s try another

15. 2 – (+7)
is the same as
2 + (-7)
2 + -7 = -5
One more…

16. 0 1 2 3 4 5 6-1-2-3-4-5-6
I like to call this,
“Stand – Turn – Walk”
Or STW
+-

17. 0 1 2 3 4 5 6-1-2-3-4-5-6
Stand at the first integer.
If the problem is -
+-
-2 + (3)
Stand at -2

19.  Since the (3) is positive, you will walk forward
from the -2 three spaces. The number you
stop on is your answer. The answer is
positive 1.
 -2 + (3) = 1

20. You have learned lots of things
About adding and subtracting
Integers. Let’s review!

21.  Rule #1 – If the signs are the same,
pretend the signs aren’t there.
Add the numbers and then put the
sign of the addends in front of
your answer.
9 + 5 = 14
-9 + -5 = -14

22.  Rule #2 – If the signs are different pretend the
signs aren’t there. Subtract the smaller from
the larger one and put the sign of the one with
the larger absolute value in front of your
answer.
-9 + +5 =
9 - 5 = 4
Larger abs. value
Answer = - 4

23. Let’s try some problems:
-6 + (3)
= -3
2 + (-4)
= -2

24. Another?
4 + (-2)
= -2
-4 + (-2)
= -6

25. Same signs add and keep
Different signs subtract

26. Keep the sign of the higher number
Then you’ll be exact

27. Same signs add and keep
Different signs subtract
Keep the sign of the higher number
Then you’ll be exact

28. Integer Subtraction Rule
Subtracting a negative number is the
same as adding a positive. Change
the signs and add.
2 – (-7)
is the same as
2 + (+7)
2 + 7 = 9!

29. Let’s try some problems:
-6 - (3)
= -9
6 - (-3)
= 9

30. Another?
4 – (-2)
= +6
-4 – (-2)
= -2

31. Same signs add and keep
Different signs subtract
Keep the sign of the higher number
Then you’ll be exact

32. Change the minus to a plus
Change the sign of next
Then all you do is add them up
As if they were a plus

33.  Same signs add and keep
 Different signs subtract
 Keep the sign of the higher number
 Then you’ll be exact
 Change the minus to a plus
 Change the sign of the next
 Then all you do is add them up
 As if they were a plus

34. Aren’t integers
interesting?