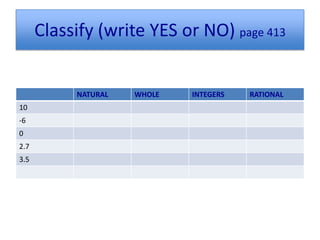
The document discusses different types of numbers: 1) Natural numbers are whole numbers starting from 1. Rational numbers can be expressed as fractions or decimals. 2) Integers include whole numbers and their opposites, as well as zero. They can be ordered and compared on a number line. 3) Rules for operating on integers include adding like signs and subtracting unlike signs, as well as products and quotients of the same or different signs being positive or negative.

1. UNDERSTANDING NUMBERS
• NATURAL NUMBERS
• WHOLE NUMBERS
• INTEGER NUMBERS
• RATIONAL NUMBERS

2. Rational Numbers
Numbers that can be expressed as a quotient of
2 integers a/b (where a and b are integers and
b is NOT 0)
Integers
Whole numbers, their opposites and zero.
Whole Numbers
Zero and natural numbers
Natural Numbers
The set of counting numbers 1, 2, 3, 4, 5, ...

3. Classify (write YES or NO) page 413
NATURAL WHOLE INTEGERS RATIONAL
10
-6
0
2.7
3.5

4. REMEMBER…
INTEGERS…
The counting numbers… 1,2,3,4…
Their opposites… -1,-2,-3,-4…
And the Zero…0
Numbers that are at the same distance from 0 are
OPPOSITES (page 408)
So we have NEGATIVE INTEGERS, POSITIVE
INTEGERS AND ZERO (neither negative or positive)

6. 8-2 COMPARING AND ORDERING
INTEGERS
• Numbers to the right of 0 on a number line are POSITIVE
• Numbers to the left of 0 on a number line are NEGATIVE
Always the numbers to the right have greater value…
• When COMPARING Integers on a number line, the Integer
that is farther to the RIGHT is allways greater
(examples A and B page 410)

8. 8-3 UNDERSTANDING RATIONAL
NUMBERS
• Numbers expressed as fractions and decimals.
• Just as there are positive and negative
integers, there are also positive and negative
fractions and decimals.
• The greater the magnitude of a negative
number, the less its value (because is farther
to the left from 0).

9. How can we order and compare
Rational Numbers?
• Sometimes it helps to write fractions as
decimals.
• SOME TIPS…
1. If you have Rational Numbers as fractions
with different whole numbers… you can
compare the whole numbers and depending on
which one is farther to the left you can
determine which rational number is less

10. more TIPS…
2. If you have Rational Numbers as fractions with
the same whole numbers… you can transform
them into decimals. This way is going to be more
easy to locate the decimals on the number line or
just to compare the decimals.
3. If you have Rational Numbers as fractions and
others as decimals… you better transform all the
fractions into decimals and then you can compare.

12. RULES FOR ADDING INTEGERS
When Adding Two Integers with the
Same sign
1. ADD the two numbers.
2. Give the answer the same sign.
SIGNS WHAT TO DO
4 18 = 22 ADD THE NUMBERS
THE SIGN OF THE ANSWER IS
-4 ( - 18 ) = - 22 ADD THE NUMBERS
THE SIGN OF THE ANSWER IS
See example E page 419

13. RULES FOR ADDING INTEGERS
When Adding Two Integers with
Different Sign
1. SUBTRACT the two numbers.
2. Give the answer the sign of the greater number.
SIGNS WHAT TO DO
SUBTRACT THE NUMBERS
THE SIGN OF THE ANSWER IS
17 ( - 29 ) = - 12 OR DEPENDING OF THE
SIGN OF THE ADDEND WITH THE
GREATER ABSOLUTE VALUE.
See example F page 419

15. IMPORTANT
It is important to understand the difference
between a minus sign and a negative sign.
They look the same, but one is an
operation between two numbers indicating
subtraction and the other tells you that a
number is negative.

16. EXAMPLES
NUMBER OR EXPRESSION HOW TO READ IT
-7 NEGATIVE SEVEN
- ( - 6) THE OPPOSITE OF NEGATIVE SIX
3-4 3 MINUS 4
3–(-4) 3 MINUS NEGATIVE 4
-6- 7 NEGATIVE 6 MINUS 7
-6–(-7) NEGATIVE 6 MINUS NEGATIVE 7

17. RULE FOR SUBTRACTING INTEGERS
Guess What?
Subtracting two Integers, is the
same as
Adding the opposite of the
second number,
to the first number!

18. SO FOLLOW THESE STEPS!
Example: – 10 – ( – 5 ) =
1. Transform the subtraction into an addition. (Change the
subtraction sign to an addition sign).
– 10 + ( – 5 ) =
2. Change the sign of the second number.
– 10 + ( 5 ) =
3. Solve the operation following the rules of Adding Integers.
(This is why it is said that subtracting … is the same as adding!)
– 10 + ( 5 ) = – 5

19. EXAMPLES
–7–(7) – 7 + (– 7) = – 14
– 15 – ( – 5 ) – 15 + ( 5 ) = – 10
22 – ( 10 ) 22 + ( – 10 ) = 12
45 – ( – 5 ) 45 + ( 5 ) = 50

20. SO, ALL YOU HAVE TO REMEMBER IS…
Two like signs ADD… and give your
answer the same sign.
Two unlike signs SUBTRACT… and
give your answer the sign of the
greater number.

22. RULES FOR MULTIPLYING INTEGERS
• The product of two integers
with the same sign is positive.
• The product of two integers
with different signs is negative.

24. RULES FOR DIVIDING INTEGERS
•
• The quotient of two integers
with the same sign is positive.
• The quotient of two integers
with different signs is negative.