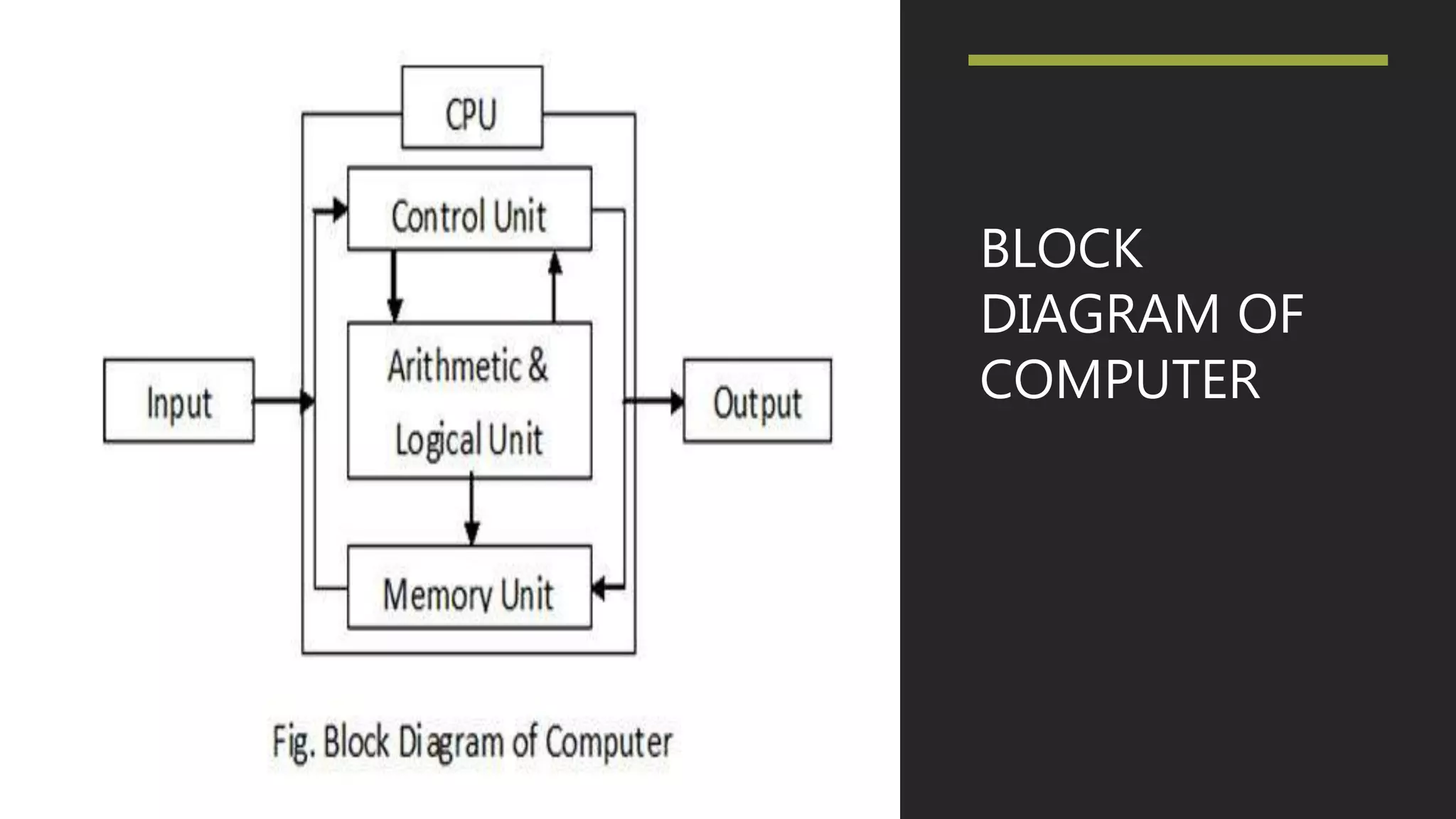
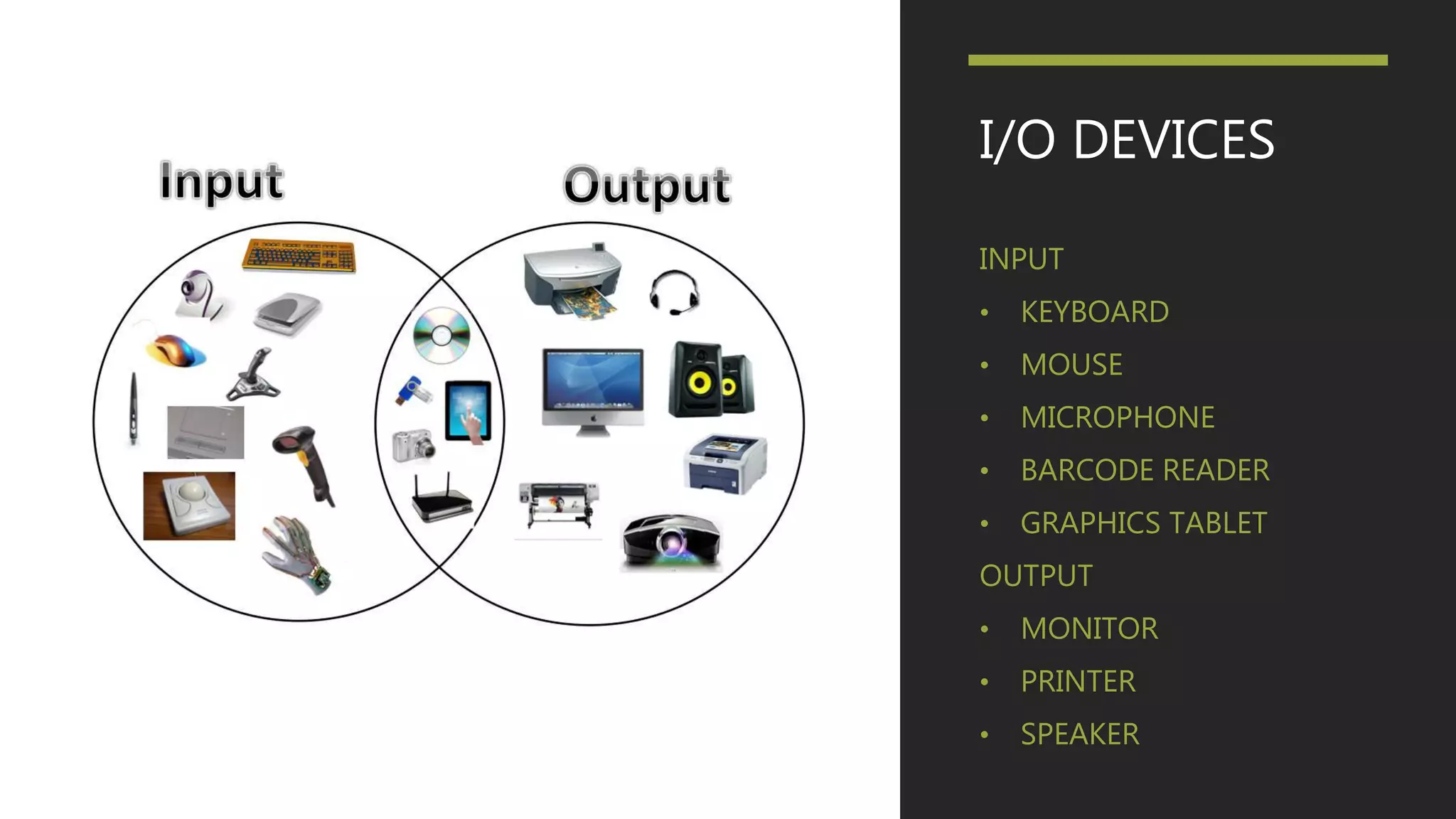
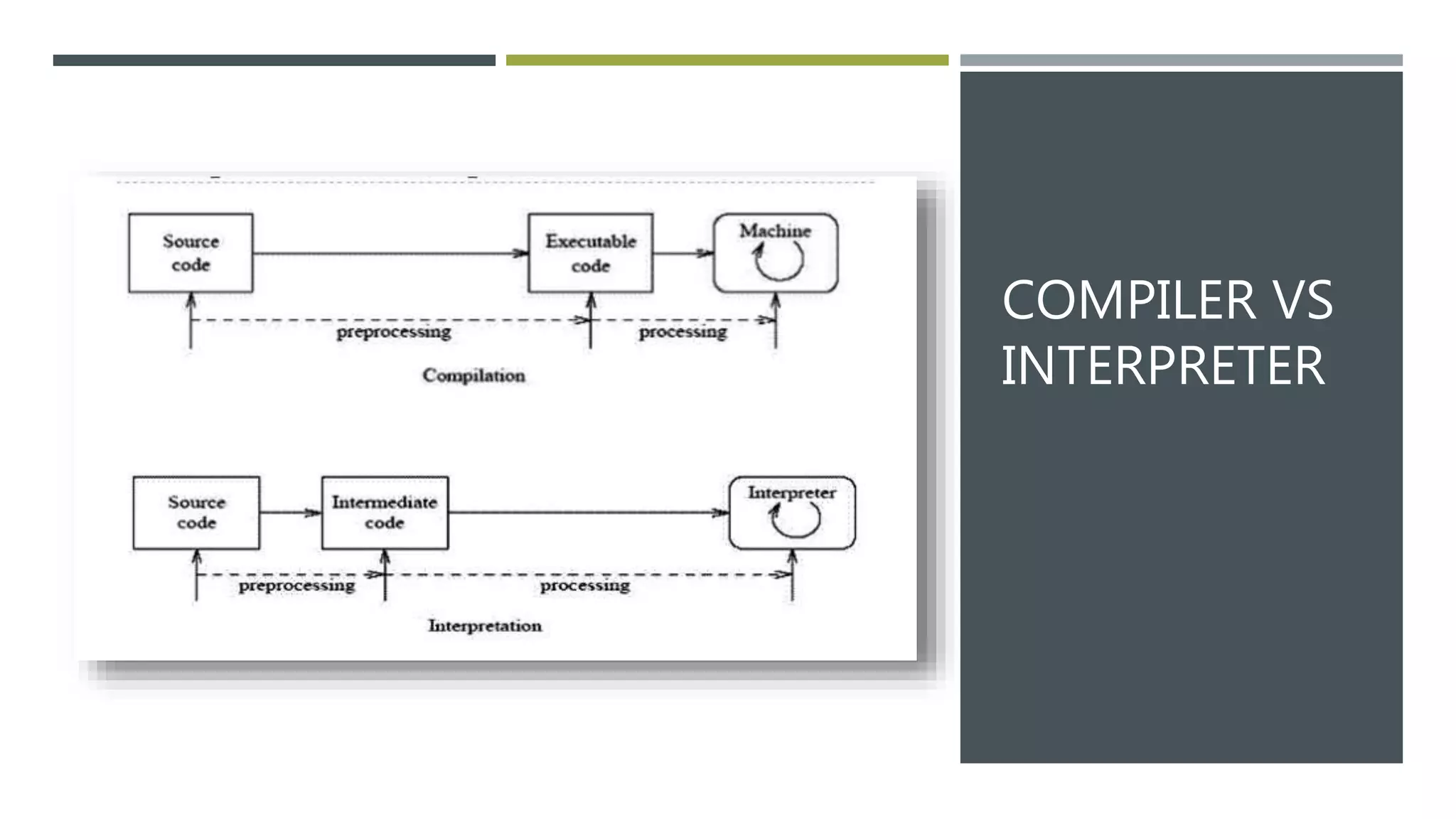
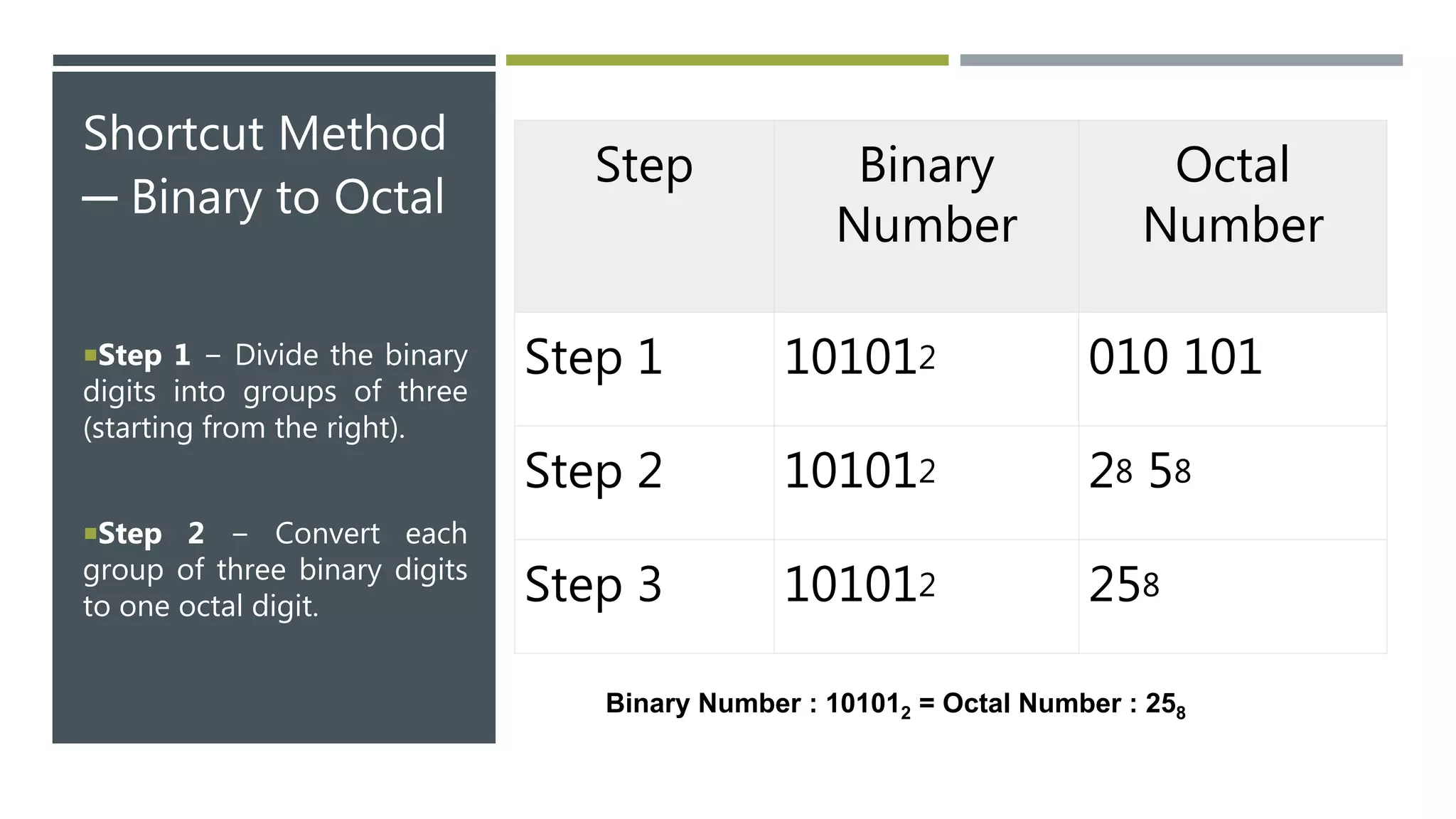
This document provides an introduction to computers and their components. It defines a computer as a machine that can carry out arithmetic and logical operations automatically according to programming instructions. It then lists and describes the major internal and external components of a computer, including the central processing unit (CPU), motherboard, memory (RAM), hard drive, graphics processing unit (GPU), power supply, input/output devices, and optical drives. It also discusses computer data representation systems such as binary, octal, decimal, and hexadecimal numbering.

1. INTRODUCTION TO COMPUTERS
CHAPTER 1

2. WHAT IS COMPUTER?
A computer is a machine that can be instructed to carry out
sequences of arithmetic or logical operations automatically
via computer programming.

3. CPU AND ITS COMPONENTS
• SYSTEM FAN
• VIDEO CARD
• MONITOR
• POWER SUPPLY
• HARD-DRIVE
• MOTHERBOARD
• OPTICAL DRIVE
• RAM
• PROCESSOR

4. MOTHERBOARD
THE MOTHERBOARD IS AT THE
CENTER OF WHAT MAKES A PC
WORK. IT HOUSES THE CPU AND IS
A HUB THAT ALL OTHER
HARDWARE RUNS THROUGH.
THE MOTHERBOARD ACTS AS A
BRAIN; ALLOCATING POWER WHERE
IT’S NEEDED, COMMUNICATING
WITH AND COORDINATING ACROSS
ALL OTHER COMPONENTS –
MAKING IT ONE OF THE MOST
IMPORTANT PIECES OF HARDWARE
IN A COMPUTER.
WHEN CHOOSING A
MOTHERBOARD, IT’S IMPORTANT
TO CHECK WHAT HARDWARE
PORTS THE MOTHERBOARD
SUPPLIES. IT’S VITAL TO CHECK
HOW MANY USB PORTS,

5. PROCESSOR
THE CPU (CENTRAL PROCESSING
UNIT OR PROCESSOR) IS
RESPONSIBLE FOR PROCESSING ALL
INFORMATION FROM PROGRAMS
RUN BY YOUR COMPUTER. THE
‘CLOCK SPEED’, OR THE SPEED AT
WHICH THE PROCESSOR
PROCESSES INFORMATION, IS
MEASURED IN GIGAHERTZ (GHZ).

6. RAM Random Access Memory, or RAM, is hardware found in the memory
slots of the motherboard. The role of RAM is to temporarily store on-the-
fly information created by programs and to do so in a way that makes
this data immediately accessible.

7. THE HARD DRIVE IS A STORAGE
DEVICE RESPONSIBLE FOR
STORING PERMANENT AND
TEMPORARY DATA.
THERE ARE TWO DIFFERENT
TYPES OF STORAGE DEVICES:
THE TRADITIONAL HARD DISK
DRIVE (HDD) AND THE NEWER
SOLID STATE DRIVES (SSD).
HARD DISK DRIVES WORK BY
WRITING BINARY DATA ONTO
SPINNING MAGNETIC DISKS
CALLED PLATTERS THAT ROTATE
AT HIGH SPEEDS, WHILE A
SOLID-STATE DRIVE STORES
DATA BY USING STATIC FLASH
MEMORY CHIPS.
HARD-DRIVE

8. GRAPHIC
PROCESSING
UNIT (GPU)
ESPECIALLY IMPORTANT FOR 3D
RENDERING, THE GPU DOES
EXACTLY WHAT ITS NAME
SUGGESTS AND PROCESSES HUGE
BATCHES OF GRAPHIC DATA. YOU
WILL FIND THAT YOUR COMPUTER’S
GRAPHICS CARD HAS AT LEAST ONE
GPU. AS OPPOSED TO THE BASIC
ON-BOARD GRAPHIC CAPABILITIES
THAT PC MOTHERBOARDS SUPPLY,
DEDICATED GRAPHICS CARDS
INTERFACE WITH THE
MOTHERBOARD VIA AN
EXPANSION SLOT TO WORK
ALMOST EXCLUSIVELY ON GRAPHIC
RENDERING.

9. POWER SUPPLY
A POWER SUPPLY UNIT,
COMMONLY ABBREVIATED AS PSU,
DOES MORE THAN JUST SUPPLY
YOUR COMPUTER WITH POWER. IT
IS THE POINT WHERE POWER
ENTERS YOUR SYSTEM FROM AN
EXTERNAL POWER SOURCE AND IS
THEN ALLOCATED BY THE
MOTHERBOARD TO INDIVIDUAL
COMPONENT HARDWARE. NOT ALL
POWER SUPPLIES ARE MADE
EQUALLY HOWEVER, AND WITHOUT
THE RIGHT WATTAGE PSU YOUR
SYSTEM WILL FAIL TO WORK.

10. BLOCK
DIAGRAM OF
COMPUTER

11. I/O DEVICES
INPUT
• KEYBOARD
• MOUSE
• MICROPHONE
• BARCODE READER
• GRAPHICS TABLET
OUTPUT
• MONITOR
• PRINTER
• SPEAKER

12. ASSEMBLER
 In computer science an assembler is a program that turns assembly language into
machine code.
 An assembler is a program that takes basic computer instructions and converts them
into a pattern of bits that the computer's processor can use to perform its basic
operations. Some people call these instructions assembler language and others use the
term assembly language.
 For example, a "Load" instruction causes the processor to move a string of bits from
a location in the processor's memory to a special holding place called a register.
Assuming the processor has at least eight registers, each numbered, the following
instruction would move the value (string of bits of a certain length) at memory location
3000 into the holding place called register 8:
 L 8,3000

13. INTERPRETER
• An interpreter is a computer program that is used to directly
execute program instructions written using one of the many
high-level programming languages.
• The interpreter transforms the high-level program into an
intermediate language that it then executes, or it could parse
the high-level source code and then performs the
commands directly, which is done line by line or statement
by statement.

14. COMPILER
• A compiler is a computer program that translates computer code
written in one programming language into another programming
language.
• The name compiler is primarily used for programs that translate
source code from a high-level programming language to a lower
level language to create an executable program

15. COMPILER VS
INTERPRETER

16. COMPILER VS
INTERPRETER

17. GENERATION OF LANGUAGES
• The first-generation languages, or 1GL are low-level languages that
are machine language.
• The second-generation languages, or 2GL are also low-level languages
that generally consist of assembly languages.
• The third-generation languages, or 3GL are high-level languages such
as C.
• The fourth-generation languages, or 4GL are languages that consist of
statements like statements in a human language. Fourth generation
languages are commonly used in database programming and scripts.
• The fifth-generation languages, or 5GL are programming languages
that contain visual tools to help develop a program. A good example
of a fifth-generation language is Visual Basic.

18. NUMBER SYSTEM
• A numeral system (or system of numeration) is a writing system
for expressing numbers; that is, a mathematical notation for
representing numbers of a given set, using digits or other
symbols in a consistent manner.
• The value of each digit in a number can be determined using −
• The digit
• The position of the digit in the number
• The base of the number system (where the base is defined as
the total number of digits available in the number system)

19. NUMBER SYSTEM IN COMPUTER SYSTEM
• Binary number system
• Octal number system
• Decimal number system
• Hexadecimal (hex) number system

20. DECIMAL NUMBER SYSTEM
• The number system that we use in our day-to-day life is the
decimal number system. Decimal number system has base 10 as
it uses 10 digits from 0 to 9. In decimal number system, the
successive positions to the left of the decimal point represent
units, tens, hundreds, thousands, and so on.
• In this computer understands everything in the multiple of 10.
• Like 721, seven in the first position of three digit number. So it
will translate 7*103

21. BINARY NUMBER SYSTEM
• Characteristics of the binary number system are as follows −
• Uses two digits, 0 and 1
• Also called as base 2 number system
• Each position in a binary number represents a 0 power of the
base (2). Example 20
• Last position in a binary number represents a x power of the
base (2). Example 2x where x represents the last position - 1.

22. NOTE − 101012 IS NORMALLY WRITTEN AS
10101.
Step Binary
Number
Decimal
Number
Step 1 101012 ((1 x 2
4
) +
(0 x 2
3
) +
(1 x 2
2
) +
(0 x 2
1
) +
(1 x 2
0
))10
Step 2 101012 (16 + 0 +
4 + 0 +
1)10
Step 3 101012 2110

23. OCTAL NUMBER SYSTEM
• Characteristics of the octal number system are as follows −
• Uses eight digits, 0,1,2,3,4,5,6,7
• Also called as base 8 number system
• Each position in an octal number represents a 0 power of the
base (8). Example 80
• Last position in an octal number represents a x power of the
base (8). Example 8x where x represents the last position - 1

24. NOTE − 125708 IS NORMALLY WRITTEN AS
12570.
Step Octal
Number
Decimal
Number
Step 1 125708 ((1 x 8
4
) + (2
x 8
3
) + (5 x
8
2
) + (7 x 8
1
)
+ (0 x 8
0
))10
Step 2 125708 (4096 +
1024 + 320
+ 56 + 0)10
Step 3 125708 549610

25. HEXADECIMAL NUMBER SYSTEM
• Characteristics of hexadecimal number system are as follows −
• Uses 10 digits and 6 letters, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D,
E, F
• Letters represent the numbers starting from 10. A = 10. B = 11,
C = 12, D = 13, E = 14, F = 15
• Also called as base 16 number system
• Each position in a hexadecimal number represents a 0 power
of the base (16). Example, 160
• Last position in a hexadecimal number represents a x power of
the base (16). Example 16x where x represents the last position
- 1

26. Note − 19FDE16 is normally written
as 19FDE.
Step Binary
Number
Decimal Number
Step 1 19FDE16 ((1 x 16
4
) + (9 x 16
3
) + (F x 16
2
) +
(D x 16
1
) + (E x 16
0
))10
Step 2 19FDE16
((1 x 16
4
) + (9 x 16
3
) + (15 x 16
2
)
+ (13 x 16
1
) + (14 x 16
0
))10
Step 3 19FDE16 (65536+ 36864 + 3840 + 208 +
14)10
Step 4 19FDE16 10646210

27. Decimal to Other Base System
• Step 1 − Divide the decimal number to be converted by the value
of the new base.
• Step 2 − Get the remainder from Step 1 as the rightmost digit (least
significant digit) of the new base number.
• Step 3 − Divide the quotient of the previous divide by the new
base.
• Step 4 − Record the remainder from Step 3 as the next digit (to the
left) of the new base number.
• Repeat Steps 3 and 4, getting remainders from right to left, until
the quotient becomes zero in Step 3.
• The last remainder thus obtained will be the Most Significant Digit
(MSD) of the new base number.

28. As mentioned in Steps 2 and 4, the
remainders have to be arranged in
the reverse order so that the first
remainder becomes the Least
Significant Digit (LSD) and the last
remainder becomes the Most
Significant Digit (MSD).
Decimal Number : 2910 = Binary
Number : 111012.
Step Operation Result Remainder
Step
1
29 / 2 14 1
Step
2
14 / 2 7 0
Step
3
7 / 2 3 1
Step
4
3 / 2 1 1
Step
5
1 / 2 0 1

29. OTHER BASE SYSTEM TO NON-DECIMAL SYSTEM
Step 1 − Convert the original number to a decimal number (base 10).
Step 2 − Convert the decimal number so obtained to the new base number.

30. Shortcut Method
─ Binary to Octal
Step 1 − Divide the binary
digits into groups of three
(starting from the right).
Step 2 − Convert each
group of three binary digits
to one octal digit.
Step Binary
Number
Octal
Number
Step 1 101012 010 101
Step 2 101012 28 58
Step 3 101012 258
Binary Number : 101012 = Octal Number : 258

31. SHORTCUT METHOD ─
OCTAL TO BINARY
Step 1 − Convert each octal
digit to a 3-digit binary number
(the octal digits may be treated
as decimal for this conversion).
Step 2 − Combine all the
resulting binary groups (of 3
digits each) into a single binary
number.
Step Octal
Number
Binary
Number
Step 1 258 210 510
Step 2 258 0102 1012
Step 3 258 0101012
Octal Number : 258 = Binary Number : 101012

32. Shortcut Method ─
Binary to
Hexadecimal
Step 1 − Divide the
binary digits into
groups of four (starting
from the right).
Step 2 − Convert each
group of four binary
digits to one
hexadecimal symbol.
Step Binary
Number
Hexadecimal
Number
Step 1 101012 0001 0101
Step 2 101012 110 510
Step 3 101012 1516
Binary Number : 101012 = Hexadecimal Number : 1516