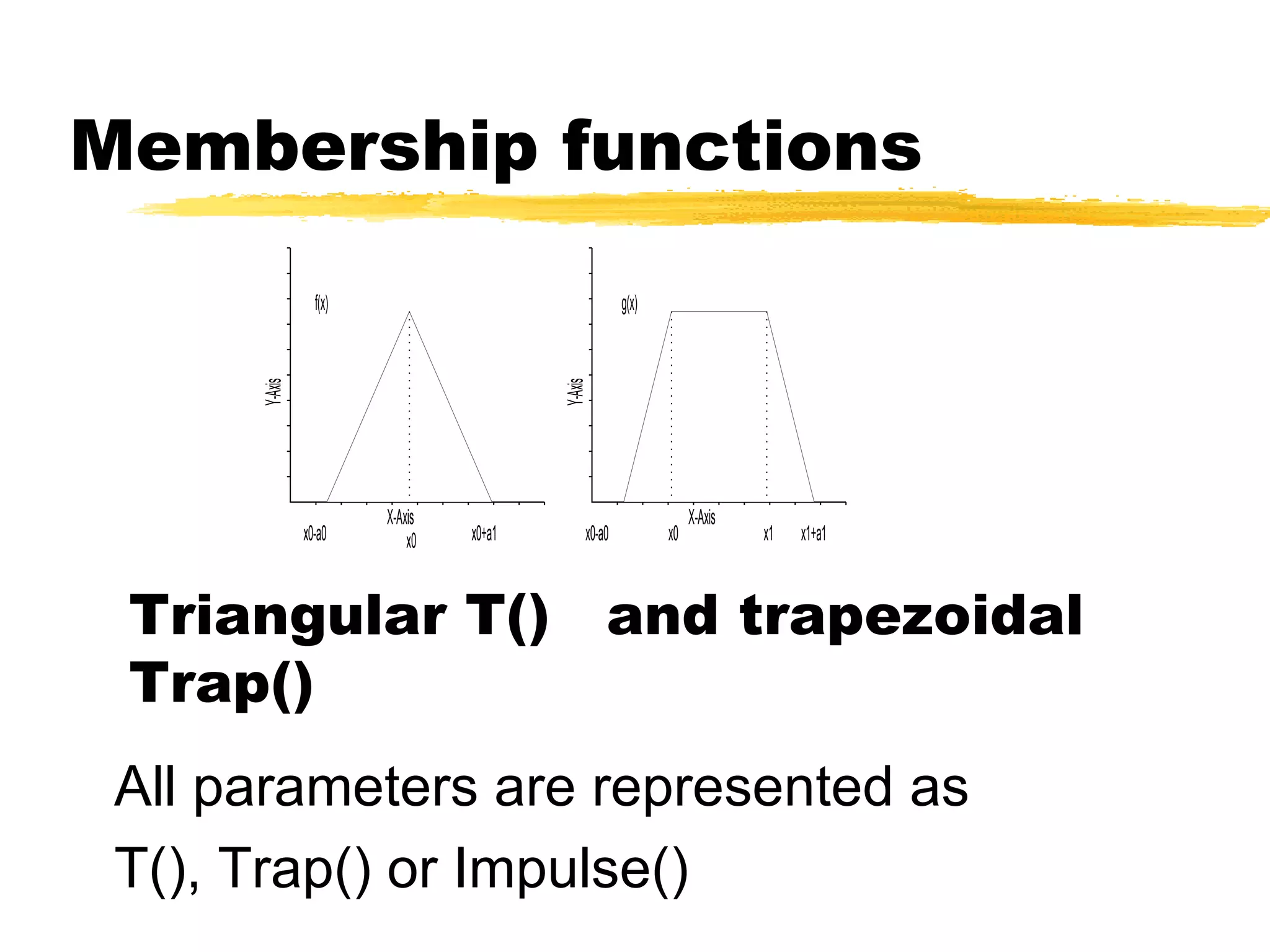
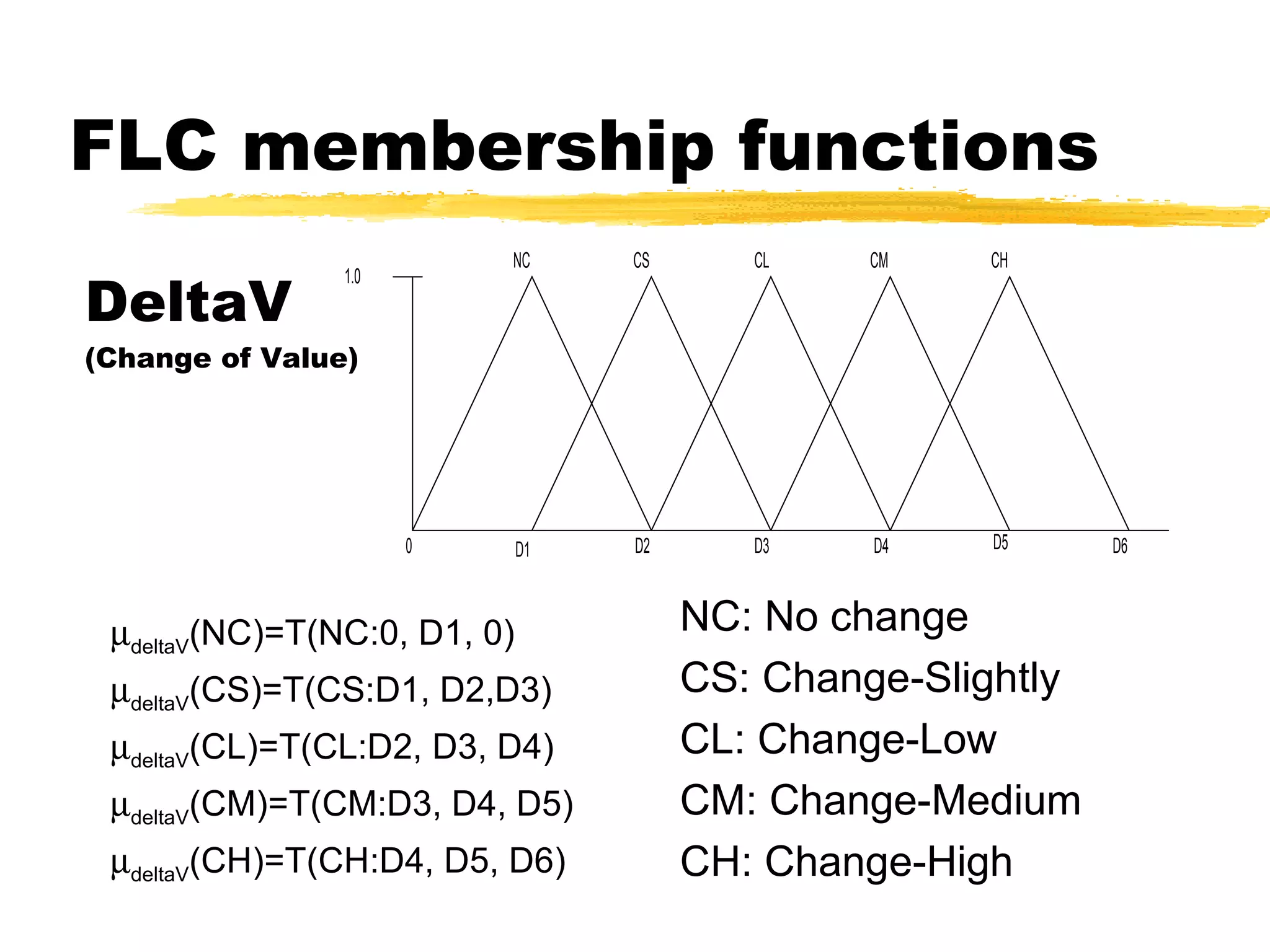
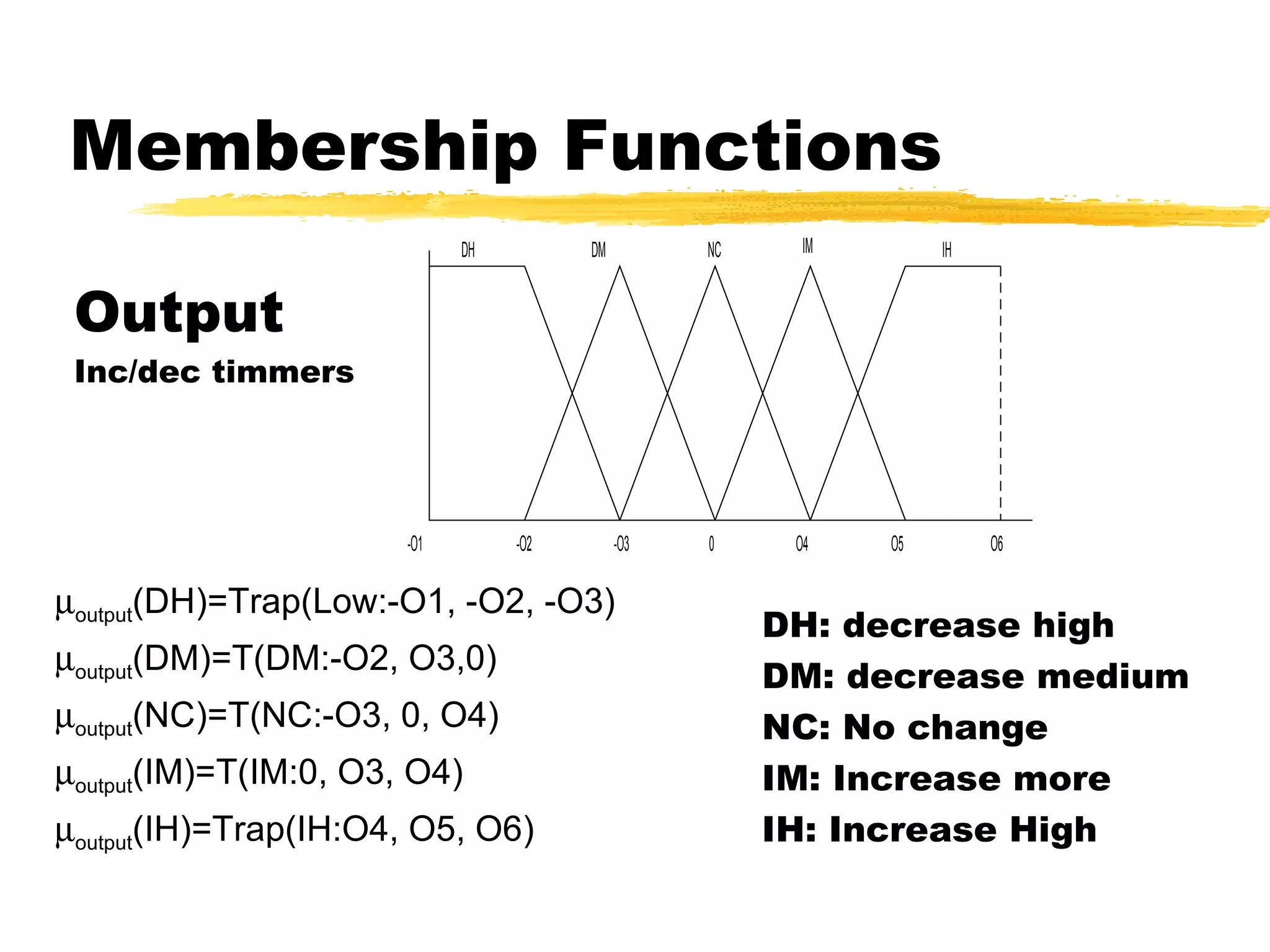
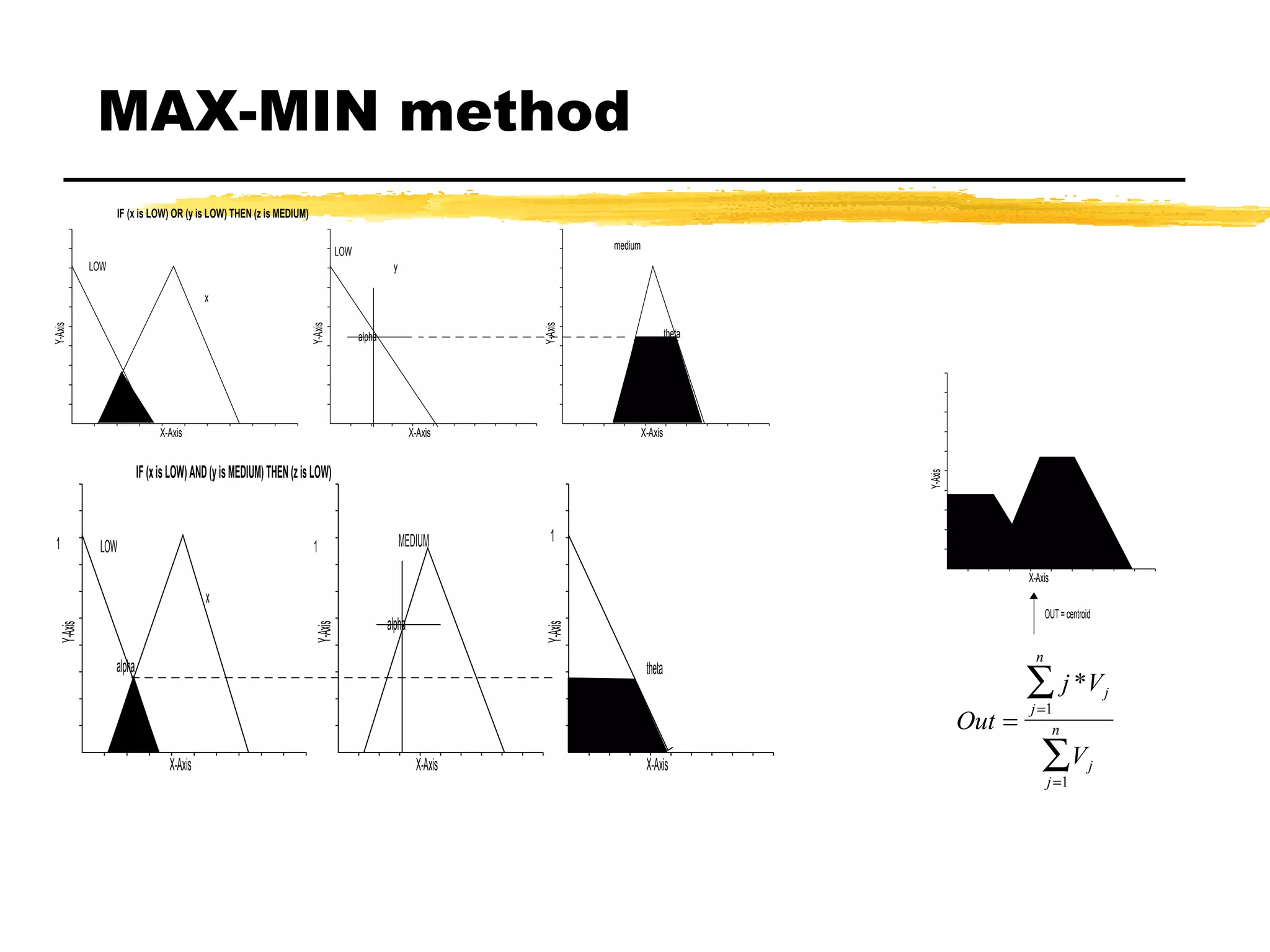
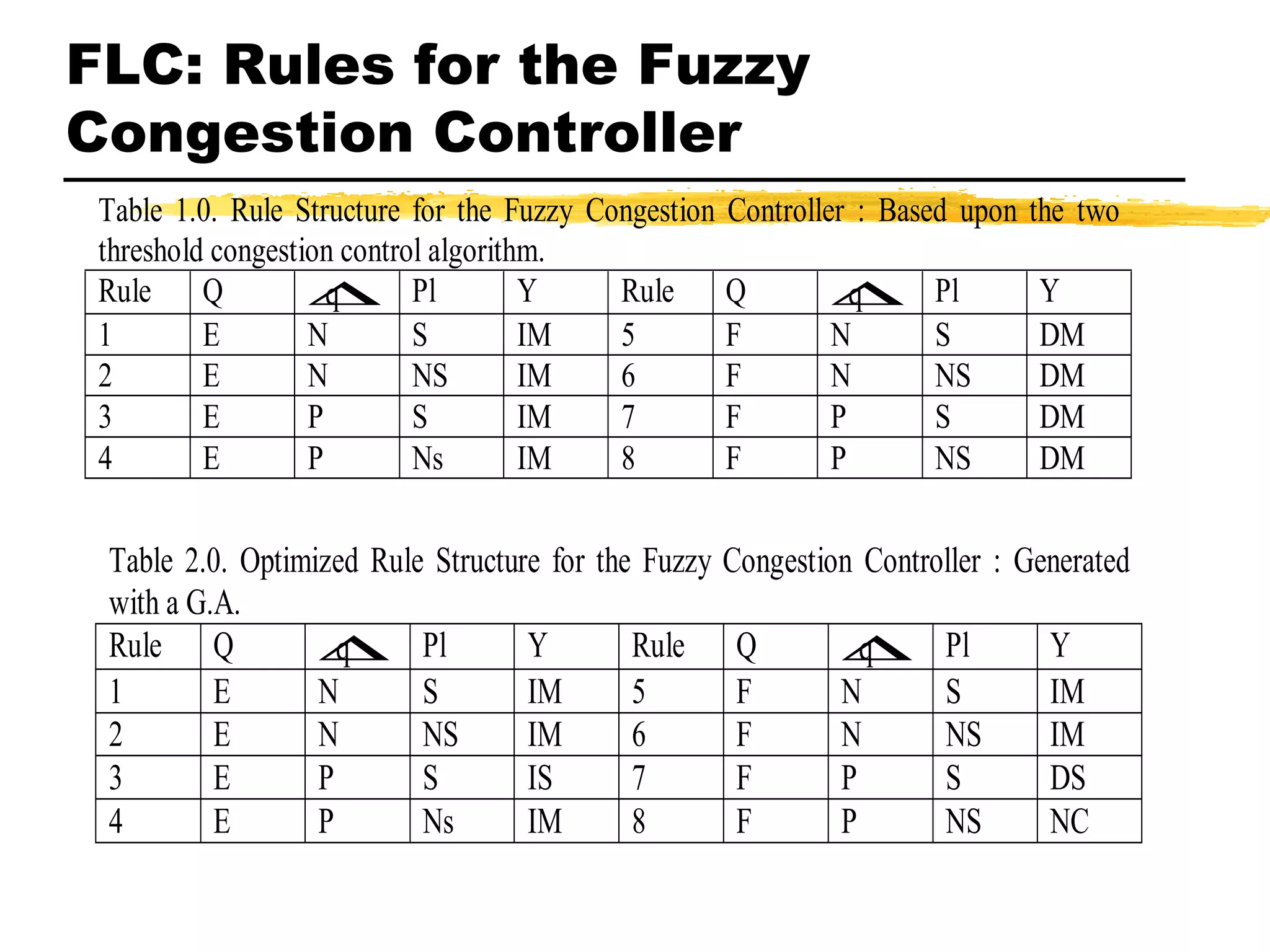
The document discusses fuzzy logic and its application to adaptive sampling. It introduces fuzzy logic concepts like membership functions and defines membership functions used for variables like deltaV and deltaT. It describes 25 rules for the fuzzy logic controller and methods for inferencing like MAX-MIN. The goal is to use a fuzzy logic approach to adaptively sample measurements based on changes in deltaV and deltaT.

1. Fuzzy Logic and Adaptive Sampling Edwin Hernandez HCS - Lab

2. INTRODUCTION In real life terms like (empty, full) are used to describe queues. Other terms could be (high congestion, average congestion, congestion, low congestion) This can be represented as : T(q) = {Empty(E), Full(F)} In fuzzy logic those variables can be represented in what it called: MEMBERSHIP FUNCTIONS

3. Membership functions Triangular T() and trapezoidal Trap() All parameters are represented as T(), Trap() or Impulse()

4. FLC membership functions  deltaV (NC)=T(NC:0, D1, 0)  deltaV (CS)=T(CS:D1, D2,D3)  deltaV (CL)=T(CL:D2, D3, D4)  deltaV (CM)=T(CM:D3, D4, D5)  deltaV (CH)=T(CH:D4, D5, D6) NC: No change CS: Change-Slightly CL: Change-Low CM: Change-Medium CH: Change-High DeltaV (Change of Value)

5. Membership functions  deltaT (Low)=Trap(Low:1, T1, T2)  deltaT (med-low)=T(med-low:T1, T2,T3)  deltaT (medium)=T(medium:T2, T3, T4)  deltaT (med-high)=T(med-high:T3, T4, T5)  deltaT (high)=Trap(high:T4, T5, Tmax) deltaT Timming

6. Membership Functions  output (DH)=Trap(Low:-O1, -O2, -O3)  output (DM)=T(DM:-O2, O3,0)  output (NC)=T(NC:-O3, 0, O4)  output (IM)=T(IM:0, O3, O4)  output (IH)=Trap(IH:O4, O5, O6) Output Inc/dec timmers DH: decrease high DM: decrease medium NC: No change IM: Increase more IH: Increase High

7. RULES RULES are simple IF X AND Y THEN Z statements. There are some techniques to process the rules, this process is called INFERENCING There are several INFERENCE methods: MAX-MIN. MAX-DOT AVERAGING ROOT SQUARES

8. Adaptive Sampling RULES There are 25 rules to be applied and used Among them: IF DeltaV=Nchange AND deltaT=Low THEN Output = IH IF DeltaV=Nchange AND deltaT=Med-Low THEN Output = IH IF DeltaV=Change-High AND DeltaT=High THEN Output = DH IF DeltaV=Change-Med AND DeltaT=Low THEN Output = NC IF DeltaV=Change-Slight AND DeltaT=High THEN OUTPUT=DM IF DeltaV=Change-Low AND DeltaT=Med THEN Output = DM

9. INFERENCING MAX-MIN: this method tests the magnitudes of each rule and selects the highest one. This method does not combine the effect of all applicable rules MAX-DOT or MAX-PRODUCT. Method scales each member function to fit under its respective peak value and takes the horizontal coordinate of the fuzzy centroid as output

10. INFERENCING AVERAGING: works but fails with contradictory rules, because it might average zero. Root Squares:it is very complicated mathematically. It combines all the applicable rules, scales the functions at their respective magnitudes and computes the fuzzy centroid of the composite area.

11. MAX-MIN method

12. MAX-DOT Pseudo-code float Output[]; Value[] = GetMembership(inputV, DeltaV[]); // returns a value for Value_chLow, Value_nochange, etc Timming[] = GetMembership(inputT, DeltaT[]); // returns a value for Timming_low, Timming_High, etc For each rule if rule[I] applies then // depending on the Rule Timming/Value applies // and are used in the array Output[] = MAX(Value[I]*Timming[I], Output[]); end; return Defuzzify(Output[])

13. Other Applications ATM Admission control and congestion control

14. FLC:ATM Switcher [1]

15. FLC : Rules and Membership functions

16. FLC: Rules for the Fuzzy Congestion Controller

17. FLC: Defuzzification Rules 1, 2, 4,5,6 apply for IM Tsukamoto’s defuzzification method

18. References/Related Work [1] R. Cheng, C. Chuang. "Design of a Fuzzy Traffic Controller for ATM Networks", IEEE/ACM Transactions on Networking, vol 4, No3., pp 460-469, June 1996. [2] V. Catania, G. Ficili, S. Palazzo, D. Panno. "A Comparative Analysis of Fuzzy versus Conventional Policing Mechanisms for ATM networks", IEEE/ACM Transactions on Networking, vol. 4, No.3, June 1996. [3] H. Li, V. Yen "Fuzzy Sets and Fuzzy Decision Making", CRC-Press, 1995. [4] A. Bonde and S. Ghosh. “A comparative Study of Fuzzy versus “fixed” thresholds for robust queue management in cell-switching networks”, IEEE/ACM Transactions on Networking Vol. 2, No. 4, August 1994, pp 337-344 [5] R. Cheng, C. Chang, L. Ling. “A QoS Neural Fuzzy Connection Admission Controller for Multimedia High-Speed Networks”, IEEE/ACM Transactions on Networking”, Vo. 7, No. 1, February 1999. [6] L. Maguire, B. Roche, T. McGinnity, et. Al. “Predicting a chaotic time series using a fuzzy neural network” Elsevier- Information Sciences, No. 112, January 1998, 125-136 [7] WEB SITE : http://www.seattlerobotics.org/encoder/mar98/fuz/f1_part1.html