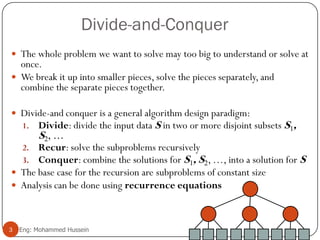
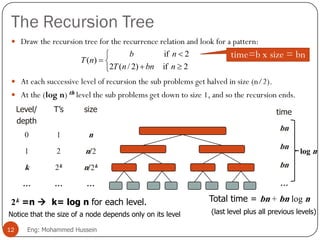
The document discusses the divide-and-conquer algorithm design paradigm. It explains that a problem is divided into smaller subproblems, the subproblems are solved independently, and then the solutions are combined. Recurrence equations can be used to analyze the running time of divide-and-conquer algorithms. The document provides examples of solving recurrences using methods like the recursion tree method and the master theorem.