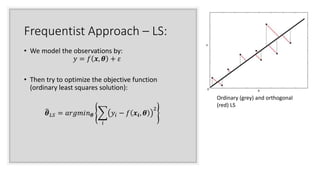
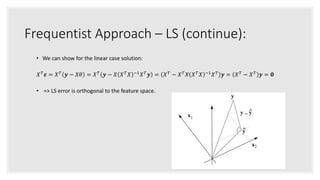
This document discusses Bayesian and frequentist approaches to statistical signal processing. It covers topics like least squares regression, maximum likelihood estimation, generalized linear models, minimum mean squared error estimation, and maximum a posteriori estimation. As examples, it discusses Gaussian, Bernoulli, and Poisson regression models within the generalized linear model framework. It also briefly covers Kalman filtering, perceptrons, and Winnow algorithms for online learning.

1. Statistical Signal
Processing
Nadav Carmel

2. Discussion Overview:
• Bayesian vs frequentist approaches:
• Conceptual differences
• Frequentist approach:
• Least-Squares
• Maximum-Likelihood
• GLM:
• Gaussian regression example (and its identity with LS)
• Bernoulli regression example (Logistic regression)
• Poisson regression example
• Bayesian approach:
• MMSE
• MAP
• Online-learning algorithms:
• Kalman filter
• Perceptron
• Winnow

3. Bayesian vs frequentist approaches
• Frequentist:
• Understand probability as a frequency of a ‘repeatable’ events.
• Bayesian:
• Understand probability as a measure of a person’s degree of belief in an
event, given the information available.

4. Frequentist Approach – LS:
• We model the observations by:
𝑦 = 𝑓 𝒙, 𝜽 + 𝜀
• Then try to optimize the objective function
(ordinary least squares solution):
𝜽 𝐿𝑆 = 𝑎𝑟𝑔𝑚𝑖𝑛 𝜽
𝑖
𝑦𝑖 − 𝑓 𝒙𝒊, 𝜽
2
Ordinary (grey) and orthogonal
(red) LS

5. Frequentist Approach – LS (continue):
• For a linear model:
𝑦 = 𝒙 𝑇
𝜽 + 𝜀
• The optimization function becomes:
𝜽 𝐿𝑆 = 𝑎𝑟𝑔𝑚𝑖𝑛 𝜽
𝑖
𝑦𝑖 − 𝒙𝑖
𝑇
𝜽
2

6. Frequentist Approach – LS (continue):
• Solutions:
• For the linear case, analytical solution exists:
𝜽 𝐿𝑆 = 𝑋 𝑇
𝑋 −1
𝑋 𝑇
𝒚
• For non-linear cases, optimization is required. Is the problem convex??
𝛻𝜃
2
𝑒 =
𝑖
𝑒𝑖 𝛻𝜃
2
𝑒𝑖 +
𝑖
𝛻𝜃 𝑒𝑖 𝛻𝜃 𝑒𝑖
𝑇
=
𝑖
𝑒𝑖 𝛻𝜃
2
𝑒𝑖 + 𝐽 𝑇 𝐽
positiveDepends on f

7. Frequentist Approach – LS (continue):
• We can show for the linear case solution:
𝑋 𝑇 𝜺 = 𝑋 𝑇 𝒚 − 𝑋𝜃 = 𝑋 𝑇 𝒚 − 𝑋 𝑋 𝑇 𝑋 −1 𝑋 𝑇 𝒚 = 𝑋 𝑇 − 𝑋 𝑇 𝑋 𝑋 𝑇 𝑋 −1 𝑋 𝑇 𝒚 = 𝑋 𝑇 − 𝑋 𝑇 𝒚 = 𝟎
• => LS error is orthogonal to the feature space.

8. Frequentist Approach – LS (continue):
• Popular LS regularizations:
𝜽 𝐿𝑆 = 𝑎𝑟𝑔𝑚𝑖𝑛 𝜽
𝑖
𝑦𝑖 − 𝑓 𝒙𝒊, 𝜽
2
+ 𝜆 𝜃 𝑝
• P = 0: Compressed Sensing (NP hard combinatorial solution)
• P = 1: LASSO (convex, non differentiable)
• P=2: ridge regression (convex and differentiable)

9. Frequentist approach – ML:
• Maximum Likelihood – a method of estimating parameters from observations with lowest error
probability.
• We assume a distribution with the parameters vector 𝜽.
• We define an objective function to optimize - the joint distribution given the observations:
𝜽 𝑀𝐿 = 𝑎𝑟𝑔𝑚𝑎𝑥 𝜽 𝑃 𝑦1, 𝑦2, … , 𝑦𝑛|𝜽

10. Frequentist approach – ML (continue):
• Under the i.i.d. assumption:
𝜽 𝑀𝐿 = 𝑎𝑟𝑔𝑚𝑎𝑥 𝜽
𝑖
𝑃 𝑦𝑖|𝜽 = 𝑎𝑟𝑔𝑚𝑎𝑥 𝜽
𝑖
𝑙𝑜𝑔 𝑃 𝑦𝑖|𝜽
• Popular regularization form:
Akaike information criterion: 𝜽 𝑀𝐿 = 𝑎𝑟𝑔𝑚𝑎𝑥 𝜽 𝑖 𝑙𝑜𝑔 𝑃 𝑦𝑖|𝜽 − 𝑘 (k – the number of free parameters)

11. Frequentist approach - GLM:
• From Wiki:
“a flexible generalization of ordinary linear regression that allows for response
variables that have a distribution other than a normal distribution”.
• 3 components for GLM:
1. Response variable from a given distribution (as in ML).
2. Explanatory variables (features).
3. A link function to the expectancy response variable: 𝐸(𝑦) = 𝑓 𝑥, 𝜃 .

12. Frequentist approach – GLM (continue):
• We model the observations by:
𝑦 = 𝑓 𝒙, 𝜽 + 𝜀
• Then try to optimize the objective function (ordinary least squares solution):
𝜽 𝐺𝐿𝑀 = 𝑎𝑟𝑔𝑚𝑎𝑥 𝜽 𝑃 𝑦1, 𝑦2, … , 𝑦𝑛|𝒙 𝟏, 𝒙 𝟐, … , 𝒙 𝒏, 𝜽
• And under the i.i.d assumption:
𝜽 𝐺𝐿𝑀 = 𝑎𝑟𝑔𝑚𝑎𝑥 𝜽
𝑖
𝑃 𝑦𝑖|𝒙𝒊, 𝜽 = 𝑎𝑟𝑔𝑚𝑎𝑥 𝜽
𝑖
𝑙𝑜𝑔 𝑃 𝑦𝑖|𝒙𝒊, 𝜽

13. Frequentist approach – GLM (continue):
• Example – Gaussian distribution:
𝑃 𝑦|𝜇, 𝜎 =
1
2𝜋𝜎
𝑒
−
𝑦 −𝜇 2
2𝜎2
• Identity link function:
𝐸 𝑦 = 𝜇 = 𝑓 𝒙, 𝜽
→ 𝑃 𝑦𝑖|𝒙𝒊, 𝜽 =
1
2𝜋𝜎
𝑒
−
𝑦 𝑖 −𝑓 𝒙 𝒊,𝜽
2
2𝜎2
• Under i.i.d. assumption:
𝜽 𝐺𝐿𝑀 = 𝑎𝑟𝑔𝑚𝑎𝑥 𝜽
𝑖
1
2𝜋𝜎
𝑒
−
𝑦 𝑖 −𝑓 𝒙 𝒊,𝜽
2
2𝜎2
= 𝑎𝑟𝑔𝑚𝑖𝑛 𝜽
𝑖
𝑦𝑖 − 𝑓 𝒙𝒊, 𝜽
2
• Identical to the LS problem 

14. Frequentist approach – GLM (continue):
• Example – Bernoulli distribution:
𝑃(𝑦|𝑝) =
𝑝, 𝑦 = 1
1 − 𝑝, 𝑦 = 0
• Logit link function:
𝐸 𝑦 = 𝑝 =
𝑒 𝜃𝑥
1 + 𝑒 𝜃𝑥
• Under i.i.d. assumption:
𝜽 𝐺𝐿𝑀 = 𝑎𝑟𝑔𝑚𝑎𝑥 𝜽
𝑖
𝑒 𝜃𝑥
1 + 𝑒 𝜃𝑥
𝑦 𝑖
1 −
𝑒 𝜃𝑥
1 + 𝑒 𝜃𝑥
1−𝑦 𝑖
• A.K.A. Logistic Regression

15. Frequentist approach – GLM (continue):
• Example – Poisson distribution:
𝑃(𝑦, |𝜆) =
𝑒−𝜆
𝜆 𝑦
𝑦!
• Logit link function:
𝐸 𝑦 = 𝜆 = 𝑒 𝜃𝑥
• Under i.i.d. assumption:
𝜽 𝐺𝐿𝑀 = 𝑎𝑟𝑔𝑚𝑎𝑥 𝜽
𝑖
𝑒−𝑒 𝜃𝑥 𝑖
𝑒 𝜃𝑥𝑦
𝑦!

16. Frequentist approach – GLM (continue):
• Possible link functions and distribution families in Spark 2.1.0:
https://spark.apache.org/docs/2.1.0/ml-classification-regression.html#available-families

17. Bayesian approach - MMSE:
• In the minimum-mean-squared-error case, we optimize the objective function:
𝑦 = 𝑎𝑟𝑔𝑚𝑖𝑛 𝑦 𝐸 𝑦|𝑥 𝑦 − 𝑦(𝑥) 2|𝑥
• Deriving the objective by 𝑦 yields:
𝜕
𝜕 𝑦
𝐸 𝑦|𝑥(𝑦2
|𝑥) − 2 𝑦 𝑥 𝐸 𝑦|𝑥(𝑦|𝑥) + 𝑦 𝑥 2
= 0 − 2𝐸 𝑦|𝑥(𝑦|𝑥) + 2 𝑦 𝑥
→ 𝑦 𝑥 = 𝐸 𝑦|𝑥(𝑦|𝑥)
• BUT, this is usually very hard to compute…

18. Bayesian approach – MMSE (continue):
• For the linear case:
𝑦 = 𝑎𝑥 + 𝑏
ℎ 𝑎, 𝑏 = 𝐸 𝑦,𝑥 𝑦 − 𝑎𝑥 − 𝑏 2
= 𝐸 𝑦 𝑦2
− 2𝑎𝐸 𝑦,𝑥 𝑥𝑦 − 2𝑏𝐸 𝑦 𝑦 + 𝑎2
𝐸 𝑥 𝑥2
+ 𝑎𝑏𝐸 𝑥 𝑥 + 𝑏2
Deriving the objective by 𝜃 = (𝑎, 𝑏) yields the closed form solution:
𝜕ℎ
𝜕𝑎
= 0,
𝜕ℎ
𝜕𝑏
= 0
→ 𝑦 =
𝐶𝑜𝑣(𝑥, 𝑦)
𝑉(𝑥)
𝑥 − 𝐸(𝑥) + 𝐸(𝑦)

19. Bayesian approach - MMSE:
• By placing the general solution, we can see that:
𝐸 𝑦|𝑥 𝑦 − 𝑦 𝜃 ∗ 𝑥
= 𝐸 𝑦|𝑥 𝑦 − 𝐸 𝑦 𝑦 𝑥 ∗ 𝑥
= 𝐸 𝑦|𝑥 𝑦 ∗ 𝑥 − 𝐸 𝑦 𝑦 𝑥 ∗ 𝑥
= 0 (Bayes Law)
=> Orthogonality is preserved between the error and the features (similar to LS)

20. Bayesian approach - MAP:
• Maximum a posteriori estimator is a method of estimating the parameter with the
lowest error probability (as in ML) given the observations and a prior knowledge.
• Our objective function is:
𝜽 = 𝑎𝑟𝑔𝑚𝑎𝑥 𝜽 𝑃(𝜽|𝒙) = 𝑎𝑟𝑔𝑚𝑎𝑥 𝜽 𝑃 𝒙 𝜽 ∗ 𝑃(𝜽)
=> When our prior in uniform, the objective is exactly identical to ML.