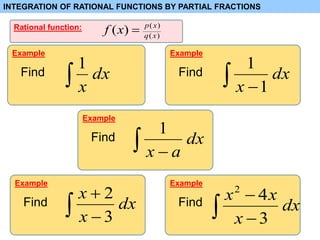
This document discusses the integration of rational functions using partial fractions. It provides examples of decomposing rational functions into partial fractions by finding the constants using techniques like covering up terms, long division, and matching coefficients. The examples cover cases where the denominators are products of linear factors and irreducible quadratic factors. After decomposing, the integrals of the individual partial fractions can be evaluated.

1. INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS
Example
Find
 dx
x
1
Example
Find
 
dx
x 1
1
Example
Find
 
dx
a
x
1
Example
Find
 

dx
x
x
3
2
Example
Find
 

dx
x
x
x
3
4
2
Rational function:
)
(
)
(
)
( x
q
x
p
x
f 

2. 2
1
2
1


 x
x 4
4
2

x
 








 dx
x
x 2
1
2
1
dx
x
  4
4
2
INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS

3. 1
1
1
1
2


 x
x )
1
)(
1
( 2
2



x
x
x
x
INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS
 


dx
x
x
x
x
)
1
)(
1
( 2
2

 


 dx
x
dx
x 1
1
1
1
2

4. 1
1
1
1
2


 x
x )
1
)(
1
( 2
2



x
x
x
x
INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS
2
1
2
1


 x
x 4
4
2

x

5. INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS
4
4
2

x 2
2 



x
B
x
A
Multiply by
)
2
)(
2
(
4



x
x
)
2
)(
2
( 
 x
x
)
2
(
)
2
(
4 


 x
B
x
A
Match coeff subsitute
)
2
2
(
)
(
4 B
A
x
B
A 



B
A

0
B
A 2
2
4 

1 subsitute
A
4
4 
2
)
2
(
)
2
(
4 


 x
B
x
A
2

x
2


x B
4
4 

3 The Heaviside
“Cover-up”
2
2 



x
B
x
A
)
2
)(
2
(
4

 x
x
Example
2

x
)
2
2
(
4


A
2
2 



x
B
x
A
)
2
)(
2
(
4

 x
x
2


x
)
2
2
(
4



B

6. INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS
16
48
3
1
4
5


 x
x
x )
1
3
)(
4
)(
4
(
1
2
2




x
x
x
linear factor
quadratic
factor quadratic
factor
irreducible
reducible
16
48
3
1
4
5


 x
x
x )
1
3
)(
2
)(
2
)(
4
(
1
2





x
x
x
x all factors are irreducible

7. INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS
)
deg(
)
deg(
if q
p 
dx
x
q
x
p
 )
(
)
( Use long division
1
)
3
2
)(
1
(
)
( 

 x
x
x
q
Factor q(x) as linear factors or irreducible quadratic
3 )
3
)(
4
(
)
( 2


 x
x
x
q
5
1
2
1
2



 x
x
x
Express p(x)/q(x) as a sum of partial fraction
4 i
i
c
bx
ax
B
Ax
b
ax
A
)
(
or
)
( 2




q(x)= product of linear factor
All distinct Some
repeated
q(x)= product of quadratic (irred)
All distinct repeated
case1
case2 case3 case4
Check if we can use subsitution
2 1
5
5
2
2



x
x
x
)
5
)(
3
)(
2
(
1


 x
x
x 2
)
3
)(
2
(
1

 x
x )
1
)(
4
(
1
2
2

 x
x 2
2
3
2
)
1
(
)
4
(
1

 x
x

8. INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS
Example
 



 dx
x
x
x
x
x
I
2
3
1
2
2
3
2
Example
Find
 
dx
x 4
1
2
q(x)= product of linear factor
All distinct Some
repeated
case1
case2
)
1
)(
2
(
1
2
2
3
1
2 2
2
3
2









x
x
x
x
x
x
x
x
x
x
1
2 




x
x
x
A B C
)
1
)(
2
(
1




A
)
1
)(
2
(
7

B
)
1
)(
1
(
2


C


 






dx
x
dx
x
dx
x
I
1
1
2
2
7
2
1
C
x
x
x 





 1
ln
2
ln
2
7
ln
2
1
Cover-up

9. INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS
Example
 





 dx
x
x
x
x
x
x
I
1
1
4
2
2
3
2
4
Example




3
2
)
1
(
)
1
(
5
x
x
x
q(x)= product of linear factor
All distinct Some
repeated
case1
case2
2
)
1
(
1 

 x
x 3
2
)
1
(
)
1
(
1 





x
x
x
A C E
D
B
Remark: only use subsitue
method or match coeff to find
the constants A,B,C,D,E.
1
4
)
1
(
1
1
4
2
2
3
2
3
2
4












x
x
x
x
x
x
x
x
x
x
x
Long
Division:
Factor: 2
2
3
)
1
)(
1
(
4
1
4





 x
x
x
x
x
x
x
2
2
)
1
(
1
1
)
1
)(
1
(
4







 x
C
x
B
x
A
x
x
x
Partial
Fraction:
Multiply: )
1
(
)
1
)(
1
(
)
1
(
4 2






 x
C
x
x
B
x
A
x
subsitute: C
x 2
4
1 


A
x 4
4
1 




C
B
A
x 



 0
0
 















 dx
x
x
x
x
I 2
)
1
(
2
1
1
1
1
1
Integrate:

10. INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS
Example



 )
3
(
)
1
(
)
1
(
1
3
2
x
x
x
q(x)= product of linear factor
All distinct Some
repeated
case1
case2
2
)
1
(
1 

 x
x 3
2
)
1
(
)
1
(
1 





x
x
x
A C E
D
B
)
3
( 

x
F

11. INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS
q(x)= product of quadratic (irred)
All distinct repeated
case3 case4
Example



 )
4
)(
1
)(
2
( 2
2
x
x
x
x
2

x 4
1 2
2




x
x
E
Dx 
C
Bx 
A
Example


 2
2
2
)
4
)(
1
( x
x
x
1
2

x
B
Ax F
Ex
2
2
2
)
4
(
4 



x
x
D
Cx
Expand by partial fraction (DONOT EVALUATE )
Expand by partial fraction (DONOT EVALUATE )

12. INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS

13. INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS

14. INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS
Expand by partial
Find the constants
Evaluate the integral