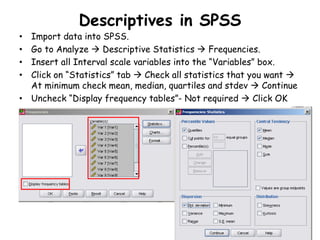
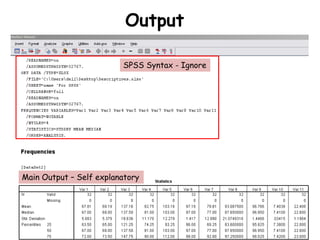
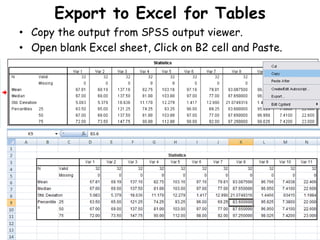
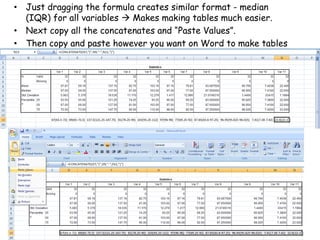
The document discusses various types of data: interval, ordinal, and nominal, along with their statistical measures such as central tendency (mean, median, mode) and dispersion (standard deviation, variance). It also explains concepts like standard error and confidence intervals, emphasizing their importance in estimating population parameters from sample statistics. Additionally, practical guidance for performing descriptive statistics using Excel and SPSS is provided.

1. Types of Variables
and
Descriptive statistics
Dhritiman Chakrabarti
Assistant Professor,
Dept of Neuroanaesthesiology
and Neurocritical Care,
NIMHANS, Bangalore

2. Types of Data
• Interval: There is a defined constant
difference between different levels of the
data.
• Ordinal: There is a hierarchical structure to
the levels of data, but the difference
between the levels is either undefined or
variable.
• Nominal: There is no hierarchy in the
structure of the data  No order in size of
values.
Increasing order of size of values
Increasing order of size of values

3. Description of Data
• Numerical Description:
1. Interval Data:
a) Measure of Central Tendency: Mean/ Median/
Mode
b) Measure of Dispersion: Variance/Standard
Deviation/Percentile/Quartile/Interquartile
range/Range
2. Ordinal Data:
a) Central Tendency: Median/Mode
b) Dispersion: Interquartile range/Range
3. Nominal Data:
Percentages/Proportions/Mode

4. Measure of Central Tendency
• Mean: Average value of all the values – Strongly
affected by extreme values and skewed distributions.
• Median: Middle most value of an ordered set of
values – Not affected by extreme values or skewed
distributions.
• Mode: Most common value of the data set – or the
value with the highest frequency.

5. Measures of Dispersion
• Range: Difference of the maximum and minimum value.
• Variance: Mean of “squared difference of individual
values from the mean”. If variance is high, the values are
highly dispersed about the mean and probably the data set
is not reliable.
• Standard Deviation: Square root of Variance.
• Coefficient of Variation: SD/Mean*100; Measure of
precision of data set; <5% is good.
• Standard Error: It’s the measure of precision WRT
population – SD of multiple sample means from the true
population mean – SD/sqrtN.
• Confidence limits: Mean ± 1.96 SE – Also a measure of
precision of data set WRT population – Used to estimate
population parameters from sample statistics.

6. Importance of SE and CI
• SE encapsulates the error in estimation of true
population mean from the sample.
• If we do multiple samplings from a population and
compute their means  Then create a histogram of
these sample means against the true population mean
 We see that the sample means follow a Normal
distribution about the true population mean.
• Conceptually: SE is the SD of these sample means
about the true population mean.
• Mathematically: SE = Sdsample /sqrt(N)
• Interpretation: That the population mean will lie
within 2 SE from the sample mean 95% of the time.

7. How to do descriptives on Excel
Mean =AVERAGE(A2:A33)
Standard Deviation =STDEV(A2:A33)
Median (50th Percentile) =MEDIAN(A2:A33)
Mode =MODE(A2:A33)
1st Quartile (25th Percentile) =QUARTILE(A2:A33,1)
3rd Quartile (75th Percentile) =QUARTILE(A2:A33,3)
Standard Error
=(STDEV(A2:A33))/(SQ
RT(COUNT(A2:A33)))
Variance =VAR(A2:A33)
Use Descriptives.xlsx  “For Excel” Sheet

8. Descriptives in SPSS
• Import data into SPSS.
• Go to Analyze  Descriptive Statistics  Frequencies.
• Insert all Interval scale variables into the “Variables” box.
• Click on “Statistics” tab  Check all statistics that you want 
At minimum check mean, median, quartiles and stdev  Continue
• Uncheck “Display frequency tables”- Not required  Click OK

9. Output
SPSS Syntax - Ignore
Main Output – Self explanatory

10. Export to Excel for Tables
• Copy the output from SPSS output viewer.
• Open blank Excel sheet, Click on B2 cell and Paste.

11. Making tables using Concatenate
• Concatenate function helps to group
different cells of Excel into one.

12. • Just dragging the formula creates similar format - median
(IQR) for all variables  Makes making tables much easier.
• Next copy all the concatenates and “Paste Values”.
• Then copy and paste however you want on Word to make tables