Multi variable calculus important steps to solveMA-123-8.pdf

of 12
MA-123: Calculus
1st
Semester
Lecture -8
Dr. Muhammad Shabbir
Assistant Professor
University of Engineering and Technology
Lahore Pakistan

of 12
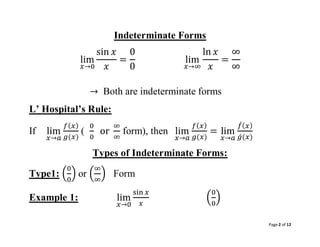
Indeterminate Forms
lim
𝑥→0
sin 𝑥
𝑥
=
0
0
lim
𝑥→∞
ln 𝑥
𝑥
=
∞
∞
→ Both are indeterminate forms
L’ Hospital’s Rule:
If lim
𝑥→𝑎
𝑓(𝑥)
𝑔(𝑥)
(
0
0
or
∞
∞
form), then lim
𝑥→𝑎
𝑓(𝑥)
𝑔(𝑥)
= lim
𝑥→𝑎
𝑓
́(𝑥)
𝑔́(𝑥)
Types of Indeterminate Forms:
Type1: (
0
0
) or (
∞
∞
) Form
Example 1: lim
𝑥→0
sin 𝑥
𝑥
(
0
0
)

of 12
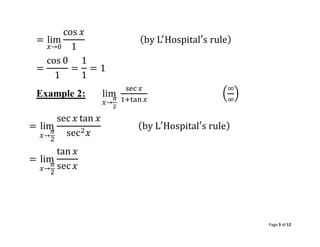
= lim
𝑥→0
cos 𝑥
1
(by L′
Hospital′s rule)
=
cos 0
1
=
1
1
= 1
Example 2: lim
𝑥→
𝜋
2
sec 𝑥
1+tan 𝑥
(
∞
∞
)
= lim
𝑥→
𝜋
2
sec 𝑥 tan 𝑥
sec2𝑥
(by L′Hospital′s rule)
= lim
𝑥→
𝜋
2
tan 𝑥
sec 𝑥

of 12
= lim
𝑥→
𝜋
2
sin 𝑥
cos 𝑥
1
cos 𝑥
= lim
𝑥→
𝜋
2
sin 𝑥
= sin
𝜋
2
= 1
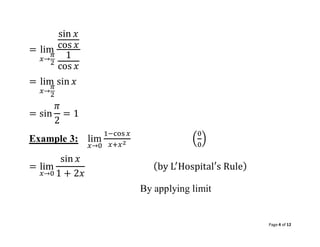
Example 3: lim
𝑥→0
1−cos 𝑥
𝑥+𝑥2
(
0
0
)
= lim
𝑥→0
sin 𝑥
1 + 2𝑥
(by L′
Hospital′s Rule)
By applying limit

of 12
=
sin 0
1 + 2(0)
=
0
1
= 0
Note: L’ Hospital’s rule is only applicable in (
0
0
) or (
∞
∞
) forms.
Type 2: (∞ × 0) or (0 × ∞) Form
We convert Type 2 into Type 1 and then apply the L’ Hospital’s
rule
Example 4: lim
𝑥→∞
𝑥(𝑎
1
𝑥 − 1) (∞ × 0)

of 12
= lim
𝑥→∞
((𝑎
1
𝑥
⁄ )−1)
1
𝑥
(
0
0
)
=
𝑎
1
𝑥
⁄
ln 𝑎 (−
1
𝑥2)
−
1
𝑥2
= 𝑎0
ln 𝑎=ln 𝑎
Type 3: (∞ − ∞) or (∞ + ∞) Form.
We convert Type 3 into Type 1 and then apply the L’ Hospital’s
rule.
Example 5: lim
𝑥→0
[
1
𝑥
− cot 𝑥] (∞ − ∞)

of 12
= lim
𝑥→0
[
1
𝑥
−
cos 𝑥
sin 𝑥
]
= lim
𝑥→0
[
sin 𝑥 − 𝑥 cos 𝑥
𝑥 sin 𝑥
] (
0
0
)
= lim
𝑥→0
[
cos 𝑥 − (−𝑥 sin 𝑥 + cos 𝑥)
𝑥 cos 𝑥 + sin 𝑥
] (by L′
Hospital′s rule)
= lim
𝑥→0
[
𝑥 sin 𝑥
] (
0
0
)
= lim
𝑥→0
[
2 cos 𝑥 − 𝑥sin 𝑥
] (by L′Hospital rule)
By applying limit
=
0 × cos 0 + sin 0
2 cos 0 − sin 0

of 12
=
0
2
= 0
Type 4: (∞0
, ∞∞
, 1∞
, 00) Form.
Example 6: lim
𝑥→0
𝑥𝑥
Let 𝑦 = 𝑥𝑥
Taking natural logarithm on both sides
ln 𝑦 = 𝑥 ln 𝑥
lim
𝑥→0
ln 𝑦 = lim
𝑥→0
𝑥 ∙ ln 𝑥 (0 × ∞)
= lim
𝑥→0
ln 𝑥
1
𝑥
(
∞
∞
)

of 12
= lim
𝑥→0
1
𝑥
−
1
𝑥2
(by L′Hospital rule)
= lim
𝑥→0
−𝑥
lim
𝑥→0
ln 𝑦 = 0
ln [lim
𝑥→0
𝑦] = 0
lim
𝑥→0
𝑦 = 𝑒0
lim
𝑥→0
𝑥𝑥
= 1
Example 7: lim
𝑥→0
(1 + 𝑥)
1
𝑥
⁄
(1∞)

of 12
Let 𝑦 = (1 + 𝑥)
1
𝑥
⁄
Taking natural logarithm on both sides
ln 𝑦 =
1
𝑥
ln(1 + 𝑥)
lim
𝑥→0
ln 𝑦 = lim
𝑥→0
1
𝑥
∙ ln(1 + 𝑥) (∞ × 0)
= lim
𝑥→0
ln(1 + 𝑥)
𝑥
(
0
0
)
= lim
𝑥→0
1
1 + 𝑥
1
(by L′
Hospital rule)
By applying limit

of 12
=
1
1 + 0
1
= 1
lim
𝑥→0
ln 𝑦 = 1 => ln [lim
𝑥→0
𝑦] = 1 => (lim
𝑥→0
𝑦 = 𝑒1
)
lim
𝑥→0
(1 + 𝑥)1/𝑥
= 𝑒
Example 8: lim
𝑥→0
𝑒𝑥−𝑒sin𝑥
𝑥−sin 𝑥
(
0
0
)
= lim
𝑥→0
(1 + 𝑥 +
𝑥2
2!
+
𝑥3
3!
+ ⋯ ) − (1 + 𝑥 +
𝑥2
2!
−
𝑥4
8!
+ ⋯ )
𝑥 − (𝑥 −
𝑥3
3! +
𝑥5
5!
+ ⋯ )

of 12
= lim
𝑥→0
(1 +
𝑥2
2!
+
𝑥3
3!
− 1 − 𝑥 −
𝑥2
2!
+
𝑥4
8!
+ ⋯ )
𝑥 − 𝑥 +
𝑥3
3!
−
𝑥5
5!
+ ⋯
‘x’ is very small so neglect 4th
and higher power of ‘x’.
= lim
𝑥→0
𝑥3
3!
⁄
𝑥3
3!
⁄
= 1
Exercise 7.5
Q (7-66) (Odd)

Multi variable calculus important steps to solveMA-123-8.pdf

More Related Content

Similar to Multi variable calculus important steps to solveMA-123-8.pdf

Recently uploaded

Multi variable calculus important steps to solveMA-123-8.pdf