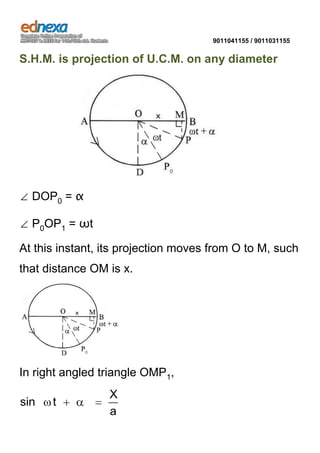
The document provides information about online courses on oscillatory motion and simple harmonic motion (S.H.M.) including live webinars, recorded lectures, online tests and solutions, notes, and career counseling. It then defines oscillatory motion and S.H.M., describing S.H.M. as periodic motion produced by a restoring force directly proportional to and opposite of the displacement. Several types and properties of S.H.M. are outlined, including the equations for displacement, velocity, acceleration, and differential equations of S.H.M. Examples and special cases are provided.

1. 9011041155 / 9011031155
Live Webinars (online lectures) with
recordings.
Online Query Solving
Online MCQ tests with detailed
solutions
Online Notes and Solved Exercises
Career Counseling

2. 9011041155 / 9011031155
Oscillation (S.H.M)
It’s a Periodic Motion
It is a motion due to vibration

3. 9011041155 / 9011031155
Oscillatory Motion
It is type of motion in which a body moves to and fro,
tracing the same path again and again, in equal
intervals of time.
What is Simple Harmonic Motion (S.H.M.)?
Simple harmonic motion is periodic motion
produced by a restoring force that is directly
proportional to the displacement and oppositely
directed.

4. 9011041155 / 9011031155
type of S.H.M.
1) If the object is moving along a straight line path,
it is called ‘linear simple harmonic motion’
(L.S.H.M.)
In S.H.M., the force causing the motion is directly
proportional to the displacement of the particle from
the mean position and directed opposite to it. If x is
the displacement of the particle from the mean
position, and f is the force acting on it, then
f α -x negative sign indicates direction of force
opposite to that of displacement
f = -kx k is called force per unit displacement or
force constant.
The units of k are N/m in M.K.S. and dyne/cm in
1 0
-2
C.G.S. Its dimensions are [M L T ]

5. 9011041155 / 9011031155
S.H.M. is projection of U.C.M. on any diameter
∠ DOP0 = α
∠ P0OP1 = ωt
At this instant, its projection moves from O to M, such
that distance OM is x.
In right angled triangle OMP1,
sin
t
X
a

6. 9011041155 / 9011031155
∴ x = a sin (ωt + α)
This is the equation of displacement of the particle
performing S.H.M. from mean position, in terms
of maximum displacement a, time t and initial
phase α.
The time derivative of this displacement is velocity v
∴v=
dx
= aω cos(ωt + α)
dt
Time derivative of this velocity is acceleration.
2
d2 x
∴ accl = 2 = - aω sin (ωt + α)
dt
n
But, a sin (ωt + α) = x,
n
2
∴ accl = - ω x

7. 9011041155 / 9011031155
The negative sigh indicates that the acceleration is
always opposite to the displacement. When the
displacement is away from the mean position, the
acceleration is towards the mean position and vice
versa. Also, its magnitude is directly proportional to
the displacement. Hence, S.H.M. is also defined as,
‘ the type of linear periodic motion, in which the
force (and acceleration) is always directed
towards the mean position and is of the
magnitude directly proportional to displacement
of the particle from the mean position.’

8. 9011041155 / 9011031155
Q.1
In the equation F=-Kx, representing a S.H.M.,
the force constant K does not depends upon
(a.) elasticity of the system
(b) inertia of the system
(c) extension or displacement of the system
(d.) velocity of the system
Q.2
The suspended mass makes 30 complete
oscillations in 15 s. What is the period and frequency
of the motion?
a) 2s,0.5 Hz
Q.3
b) 0.5s, 2Hz
c) 2s,2Hz d)0.5s,0.5Hz
A 4-kg mass suspended from a spring
produces a displacement of 20 cm. What is the
spring constant
a) 196 N/m b) 500 N/m
c) 100 N/m
d) 80N/m

9. 9011041155 / 9011031155
Answers :1.
(d.) velocity of the system
2.
(b) 0.5s, 2Hz
15 s
0.50 s
30 cylces
Period : T
0.500 s
1
1
f
T 0.500 s
Frequency : f 2.00 Hz
T
3. a) 196 N/m
F
4 kg (9.8 m / s2)
F 39.2
k
X
0.2
196 N / m
39.2 N

10. 9011041155 / 9011031155
Differential Equation of S.H.M.
If x is the displacement of the particle performing
S.H.M.,
d2 x
accln = 2 ,
dt
d2 x
force = m 2
dt
But f = - kx
d2 x
∴ m 2 = - kx
dt
d2 x
∴ m 2 + kx = 0 ... (1)
dt
d2 x
k
∴ 2 +
x
m
dt
0 But,
k
m
2
2
d2 x
∴
+ ω x = 0 ... (2)
2
dt
These two equations are called differential equations
of S.H.M.
According to second equation,

11. 9011041155 / 9011031155
Force = mass × acceleration
2
∴ f = - mω x
but, f = - kx also
2
∴ - kx = - mω x
2
∴ k = mω
∴ k/m = ω
2

12. 9011041155 / 9011031155
Formula for velocity
d2 x
= - ω2x
dt 2
d2 x
dt 2
d dx
dt dt
d dx
dv
But,
dt dt
dt
dv dv dx
x
dt dx dt
dx
v
dt
d2 x
dv
v
dx
dt 2
dv
2
v
x
dx
But,
Separating the variables,
2
v dv = - ω x dx
integrating both sides,
v dv
2
x dx

13. 9011041155 / 9011031155
2
2 x
v2
∴
=-ω
2
2
C
Where C is constant of integration.
at x = a, v = 0
∴0=
∴C=
v2
2
v2
v2
v
2 2
a
2
C
2
a2
2
2
x2
2
2 2
a
2
2 2
a
2
2
x2
a2 x 2
a2 x 2

14. 9011041155 / 9011031155
Formula for displacement
dx
dt
But, v
dx
dt
a2
x2
dx
a
2
x
dt
2
Integrating both sides,
dx
a
2
x
∴ sin-1
dt
2
x
a
t
where α is constant of integration. It is the initial
phase of motion.
x
a
x
sin
a sin
t
t

15. 9011041155 / 9011031155
Special Cases
1. At t = 0, x = 0
0 = a sin α
∴ sin α = 0
∴ α = 0 Thus, when the body starts moving from
the mean position, the initial phase is zero.
2. At t = 0, x = a
a = a sin α
∴ sin α = 1
∴ α = π / 2 Thus, when the body starts moving
from the extreme position, the initial phase angle
is π / 2

16. 9011041155 / 9011031155

Ask Your Doubts

For inquiry and registration, call 9011041155 /
9011031155.