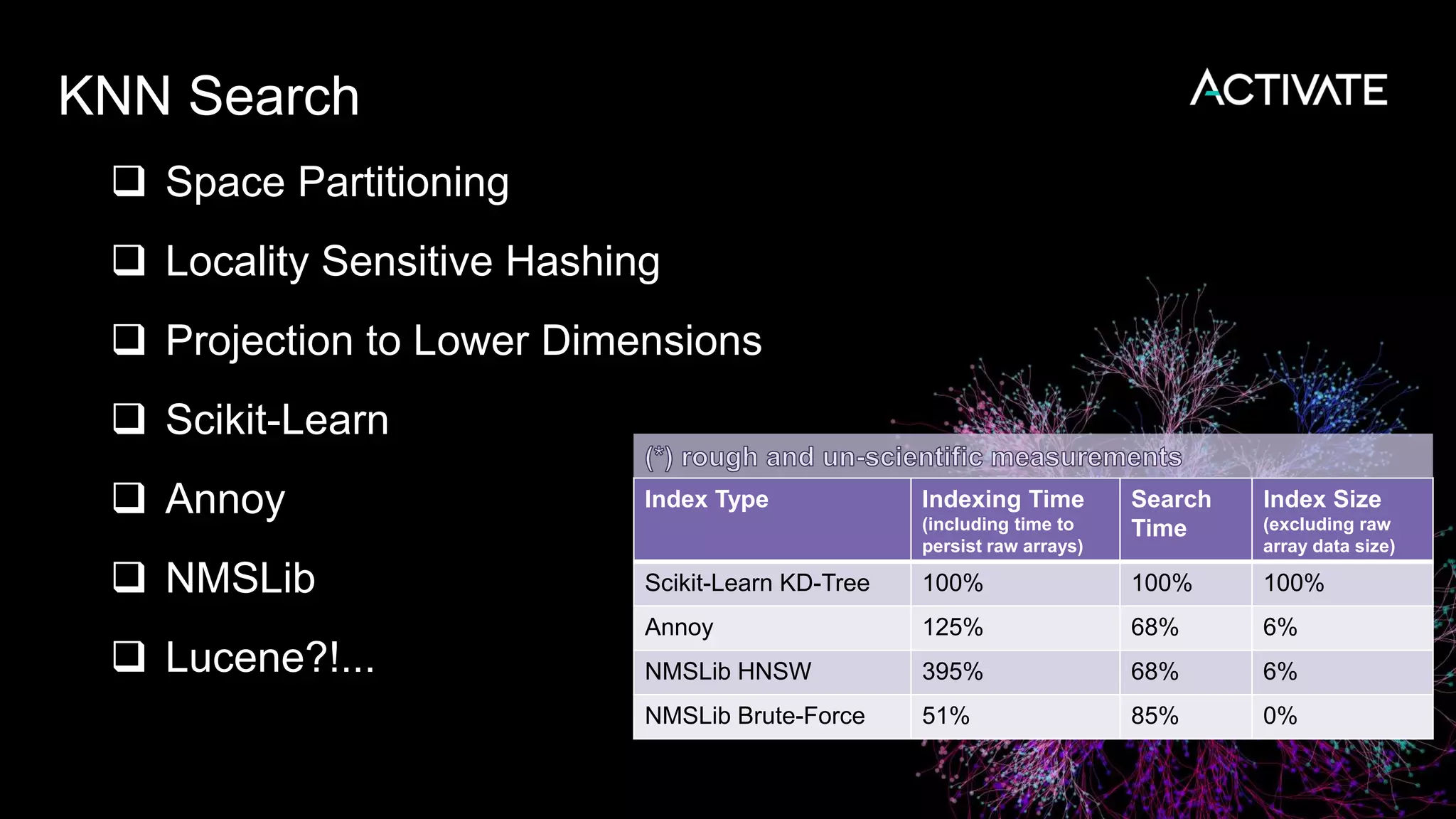
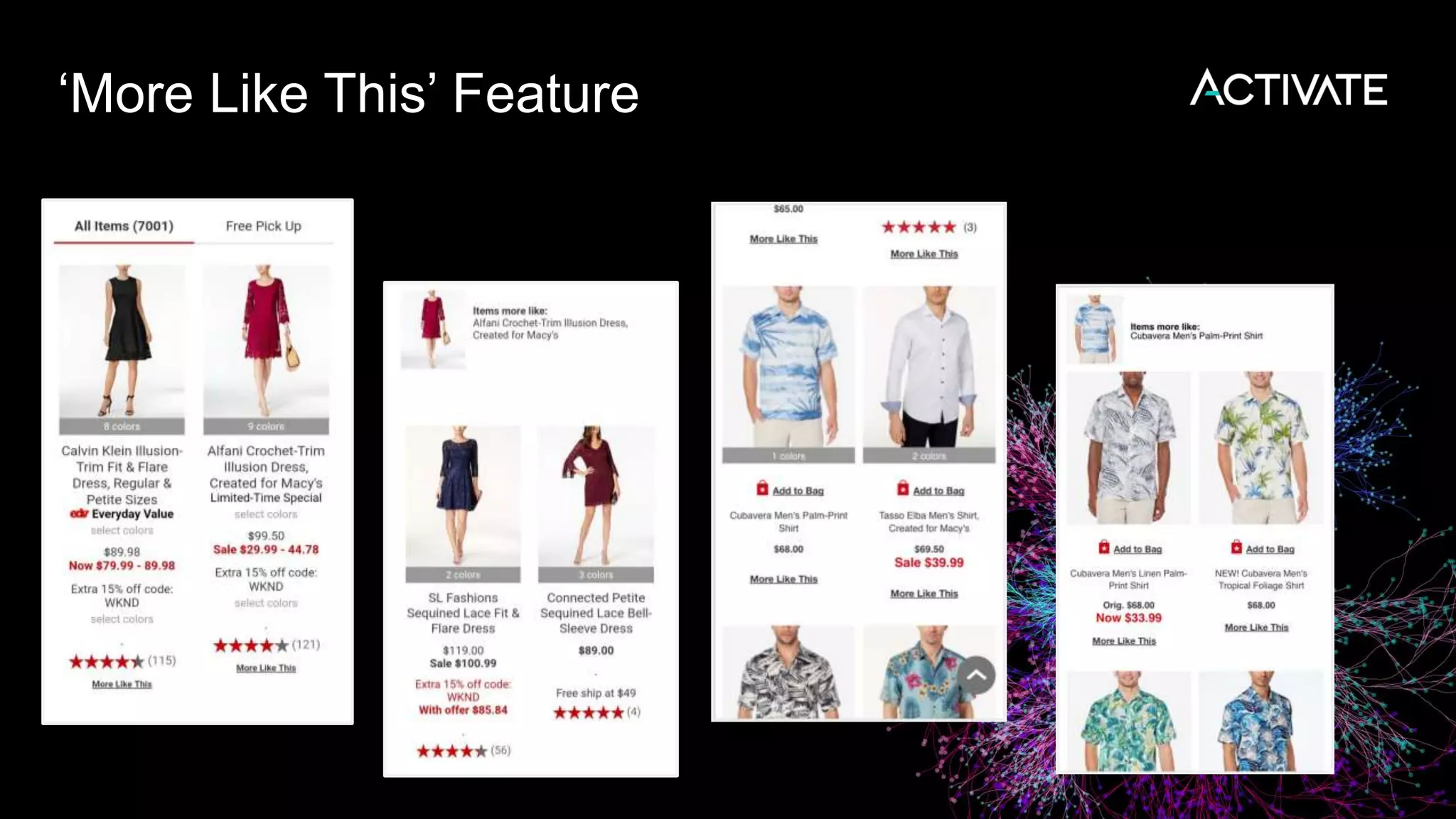
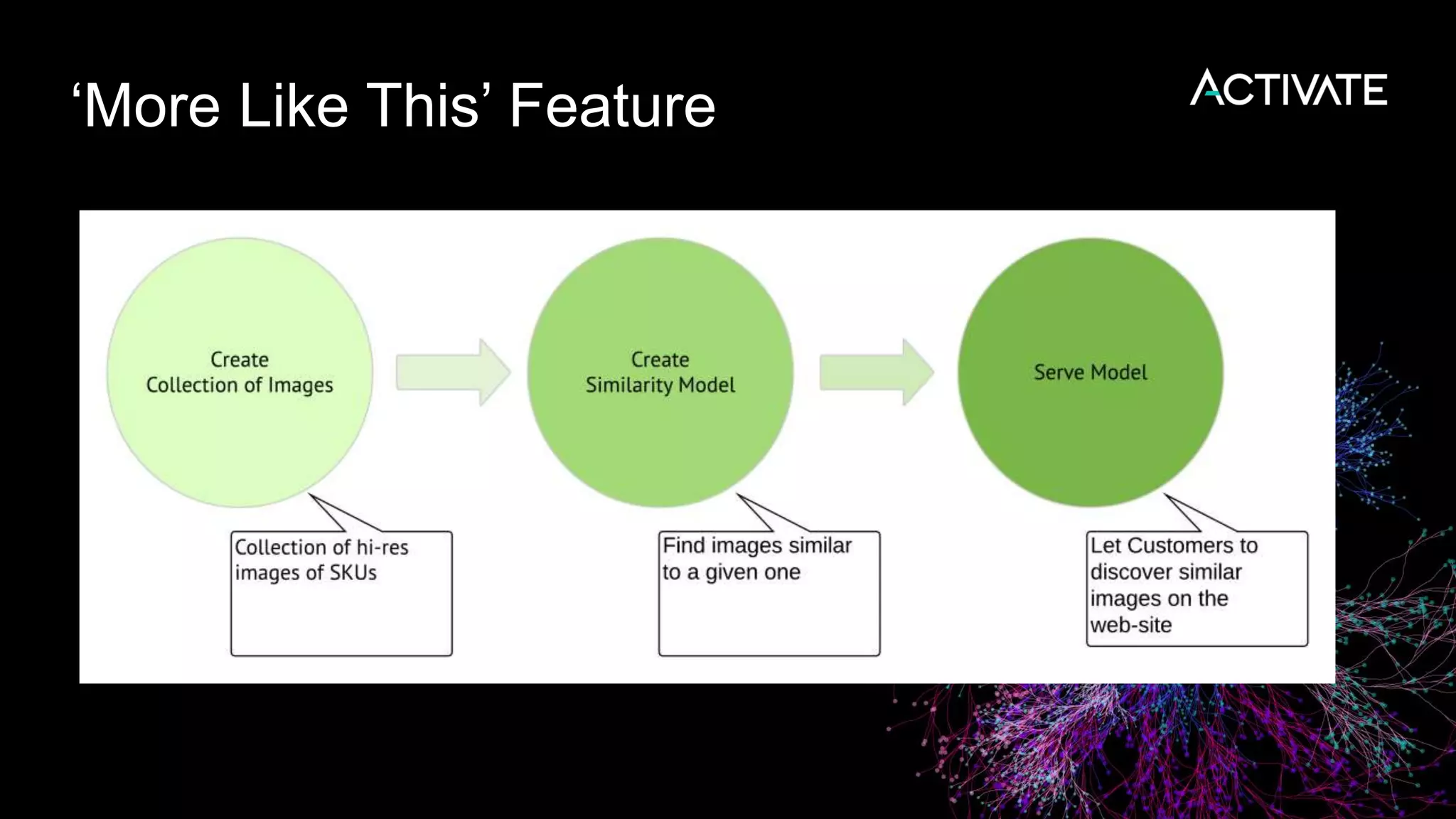
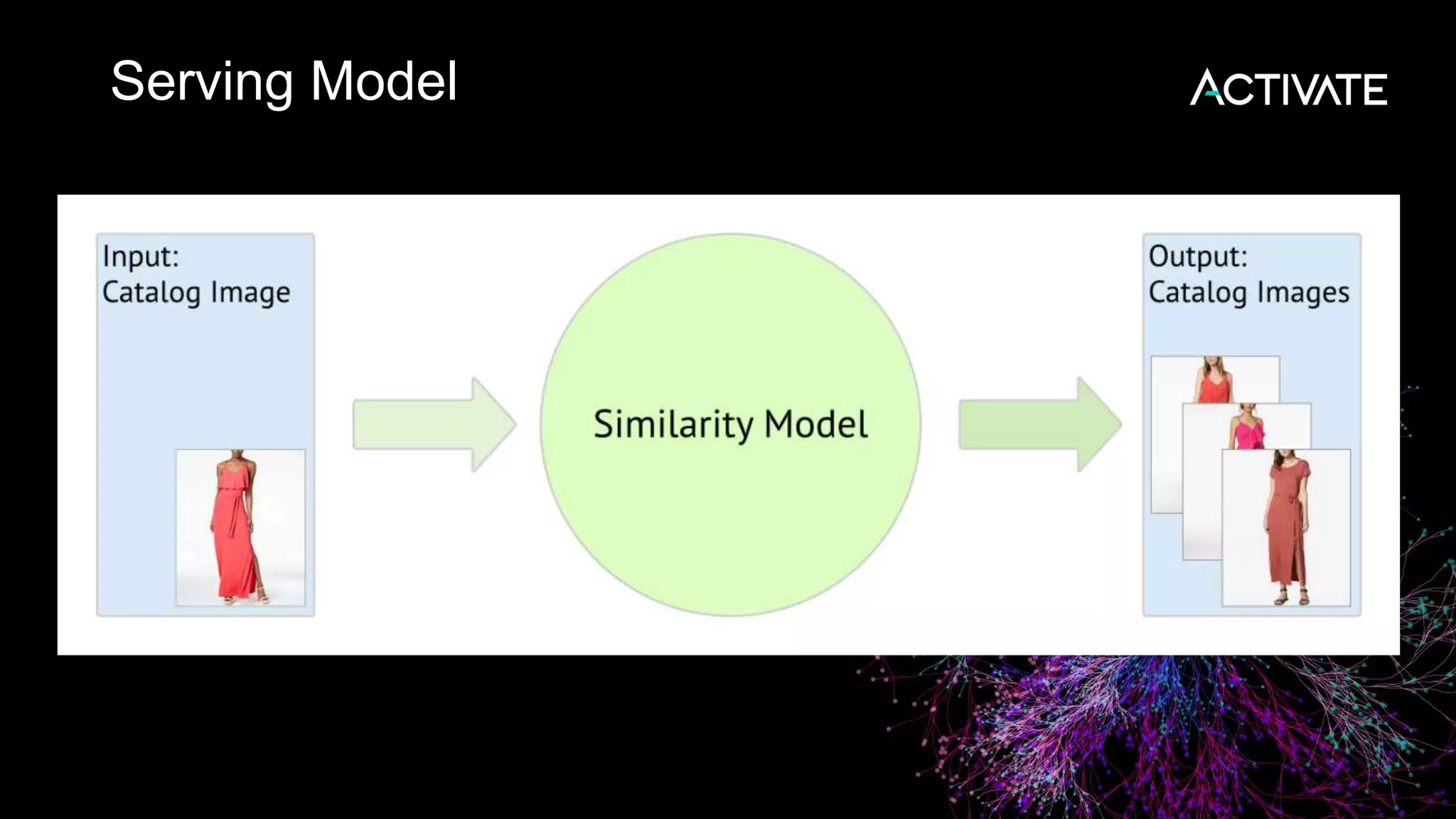
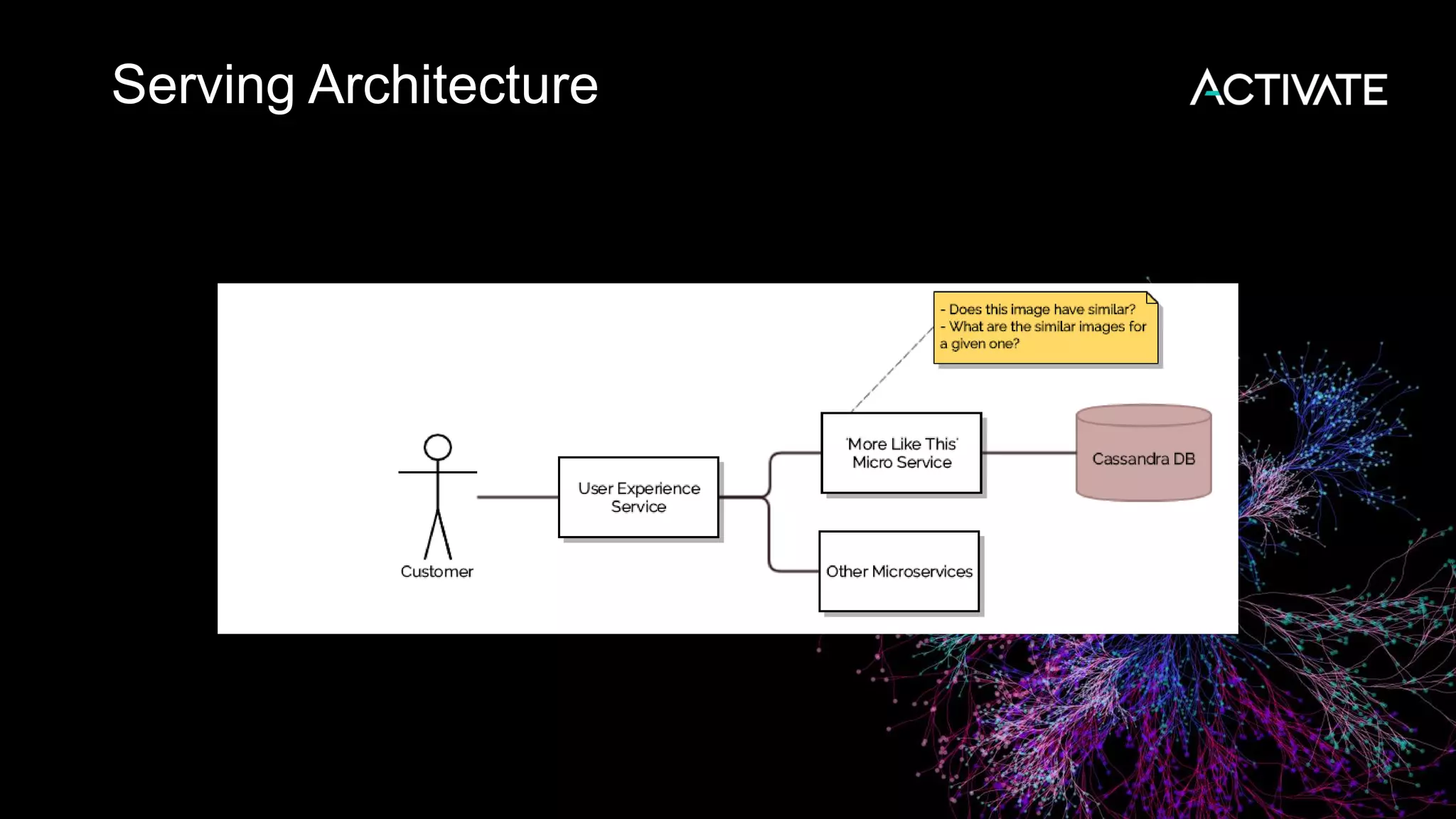
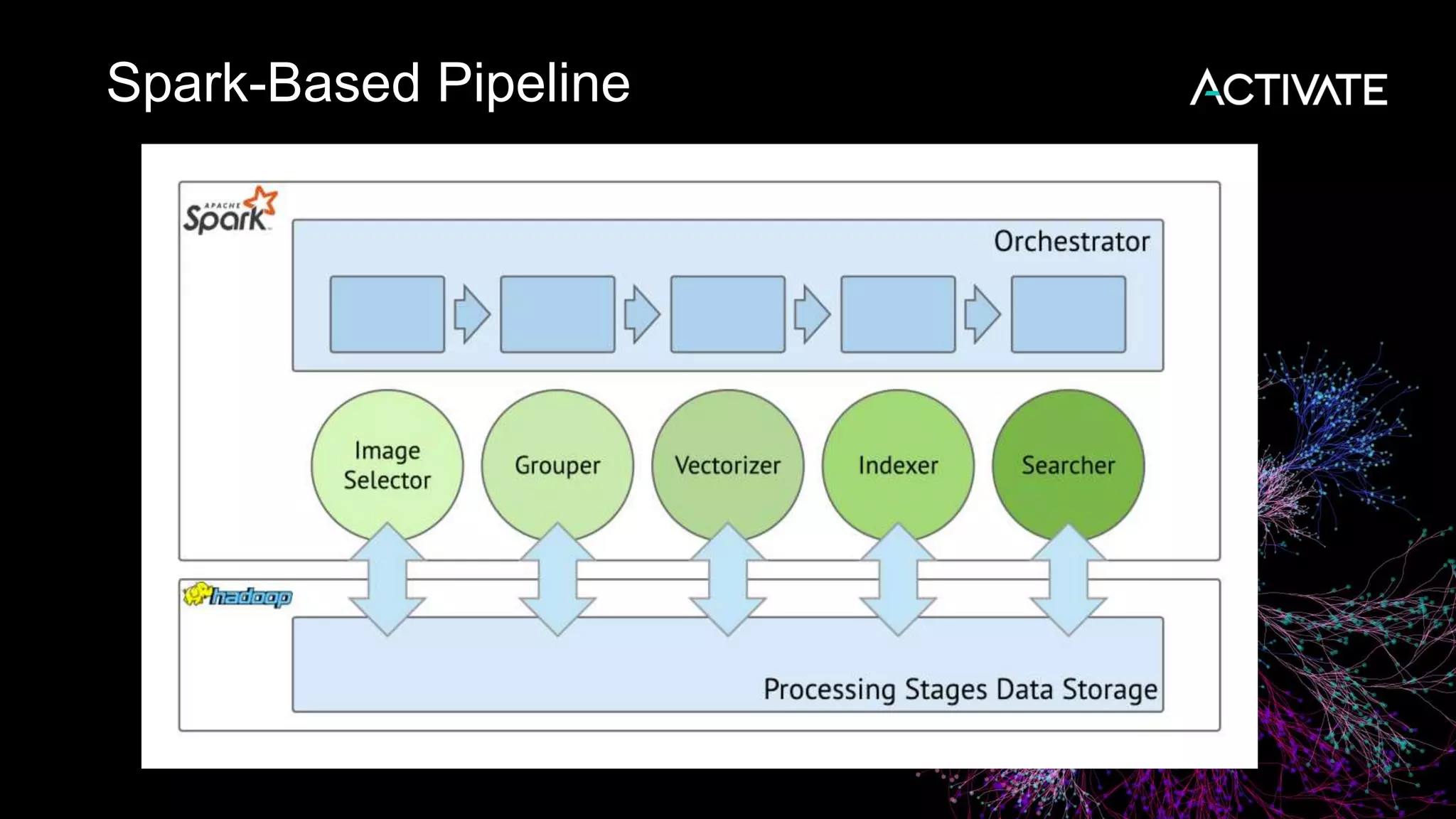
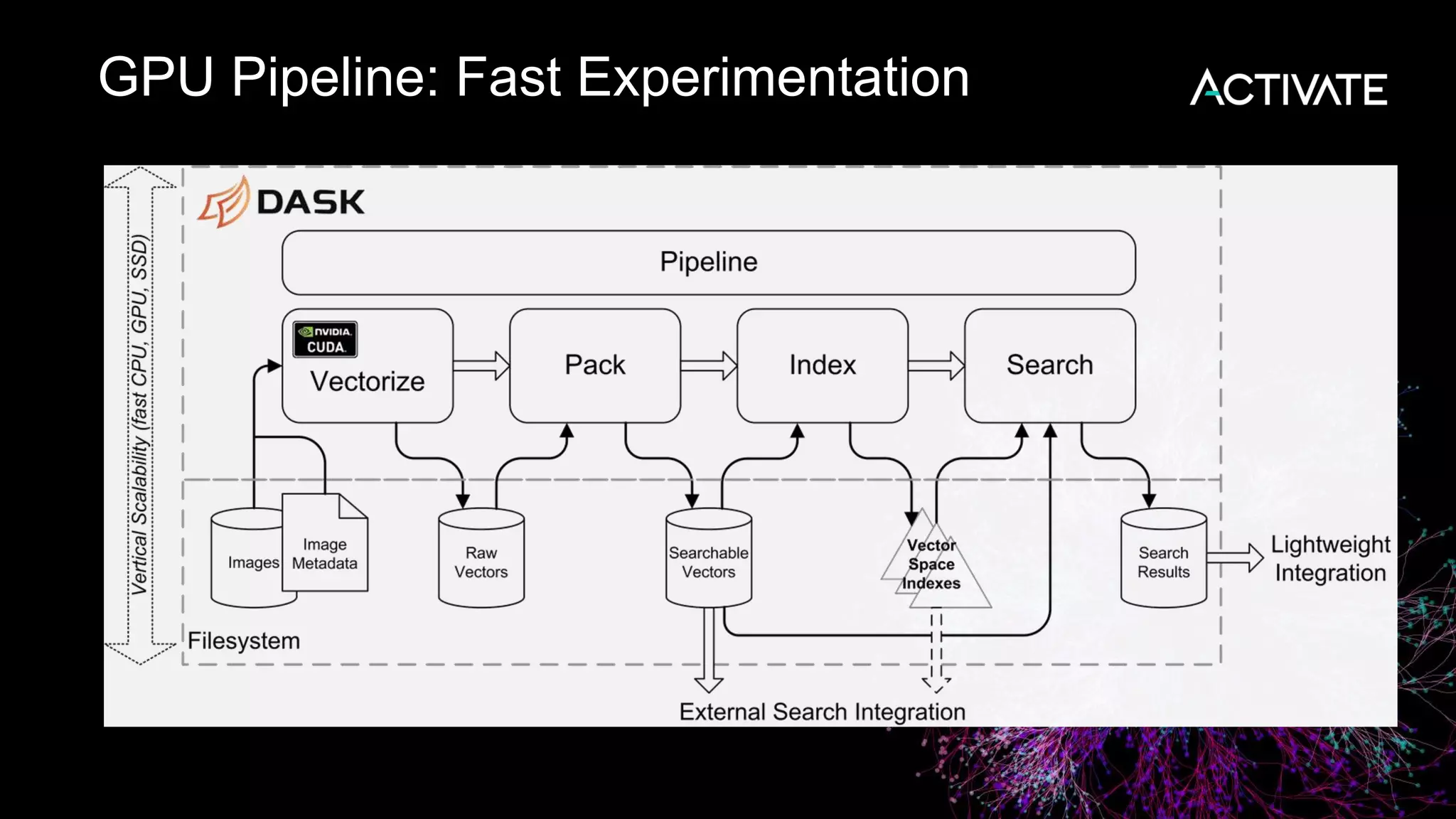
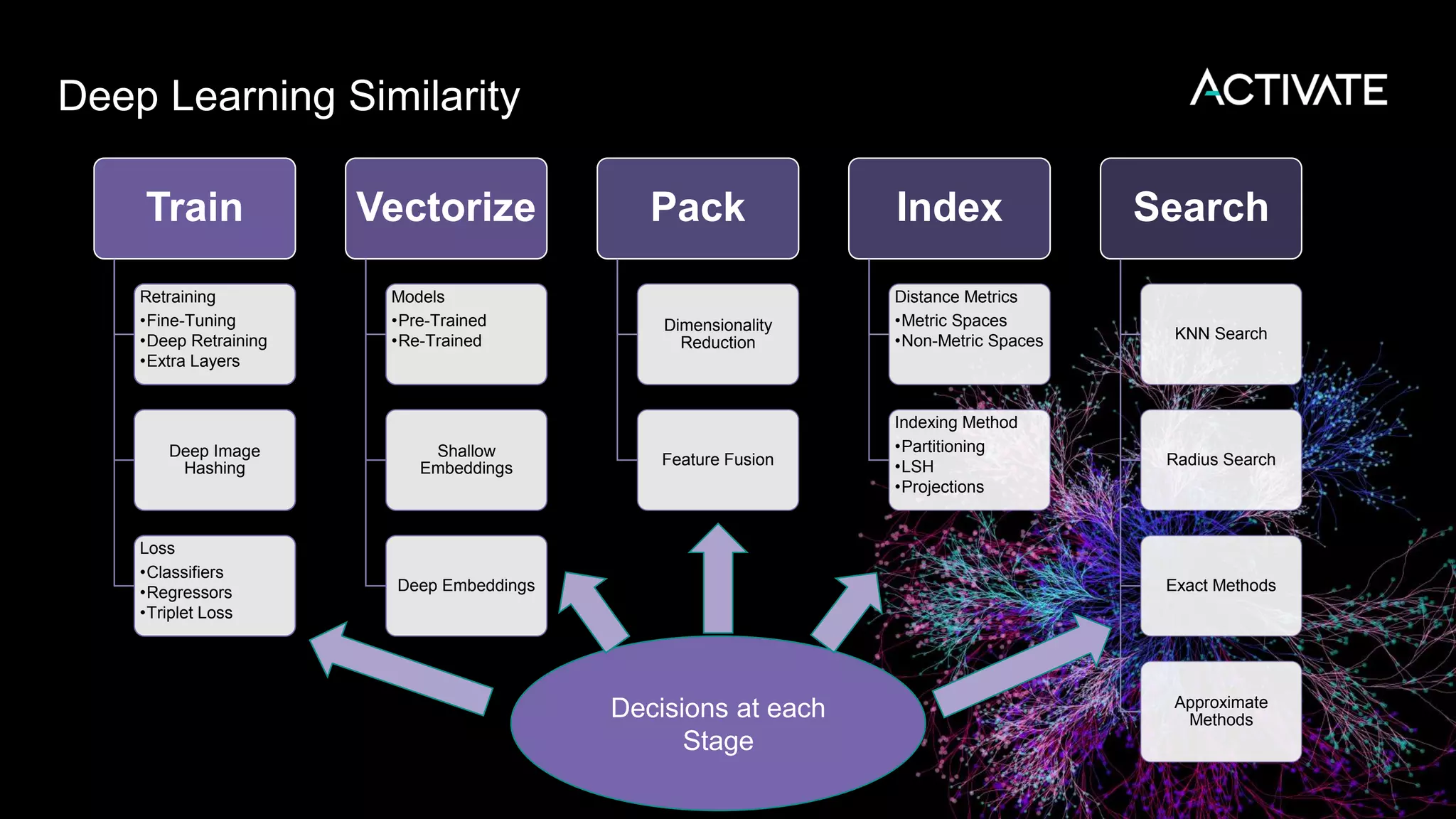
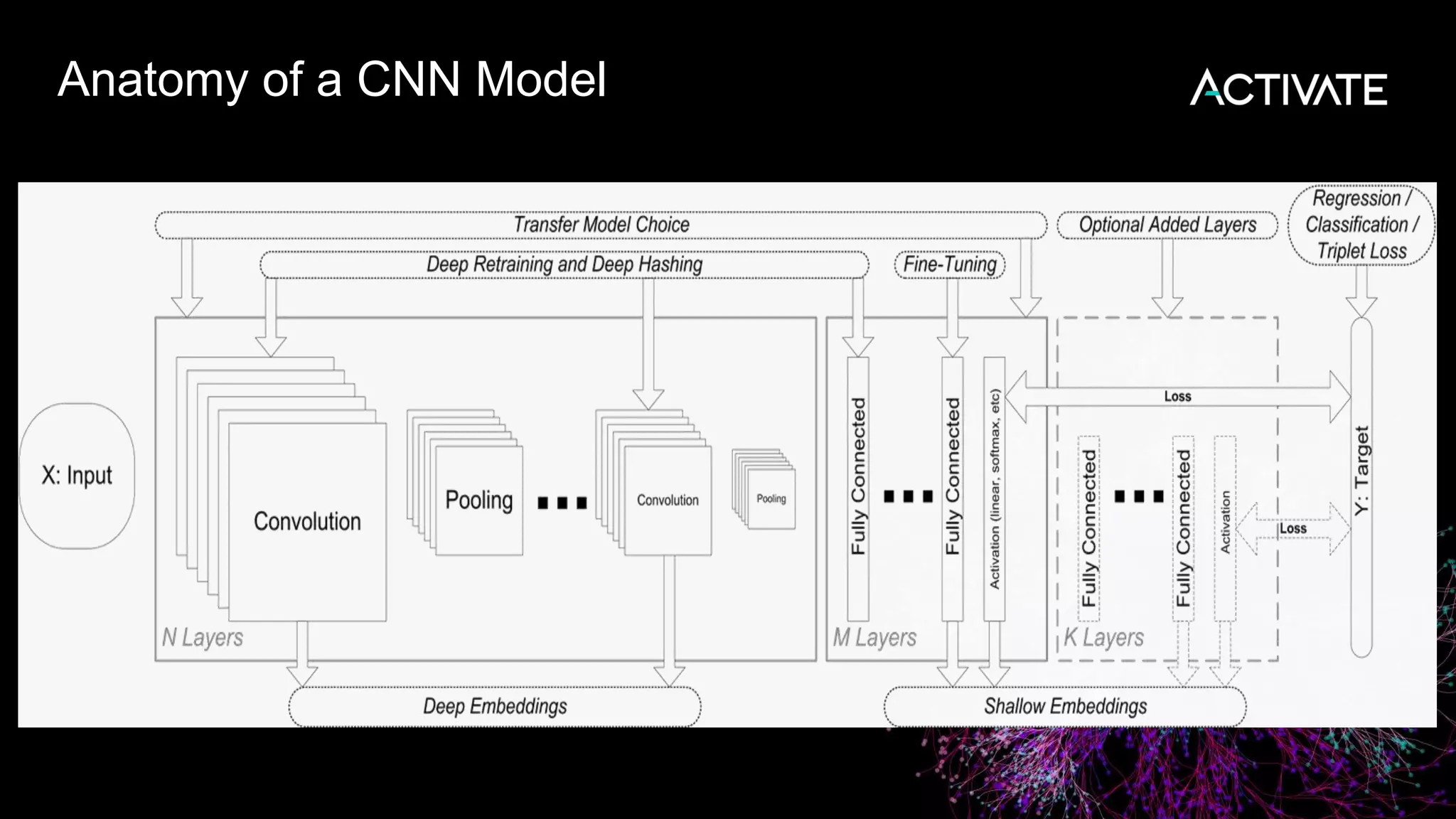
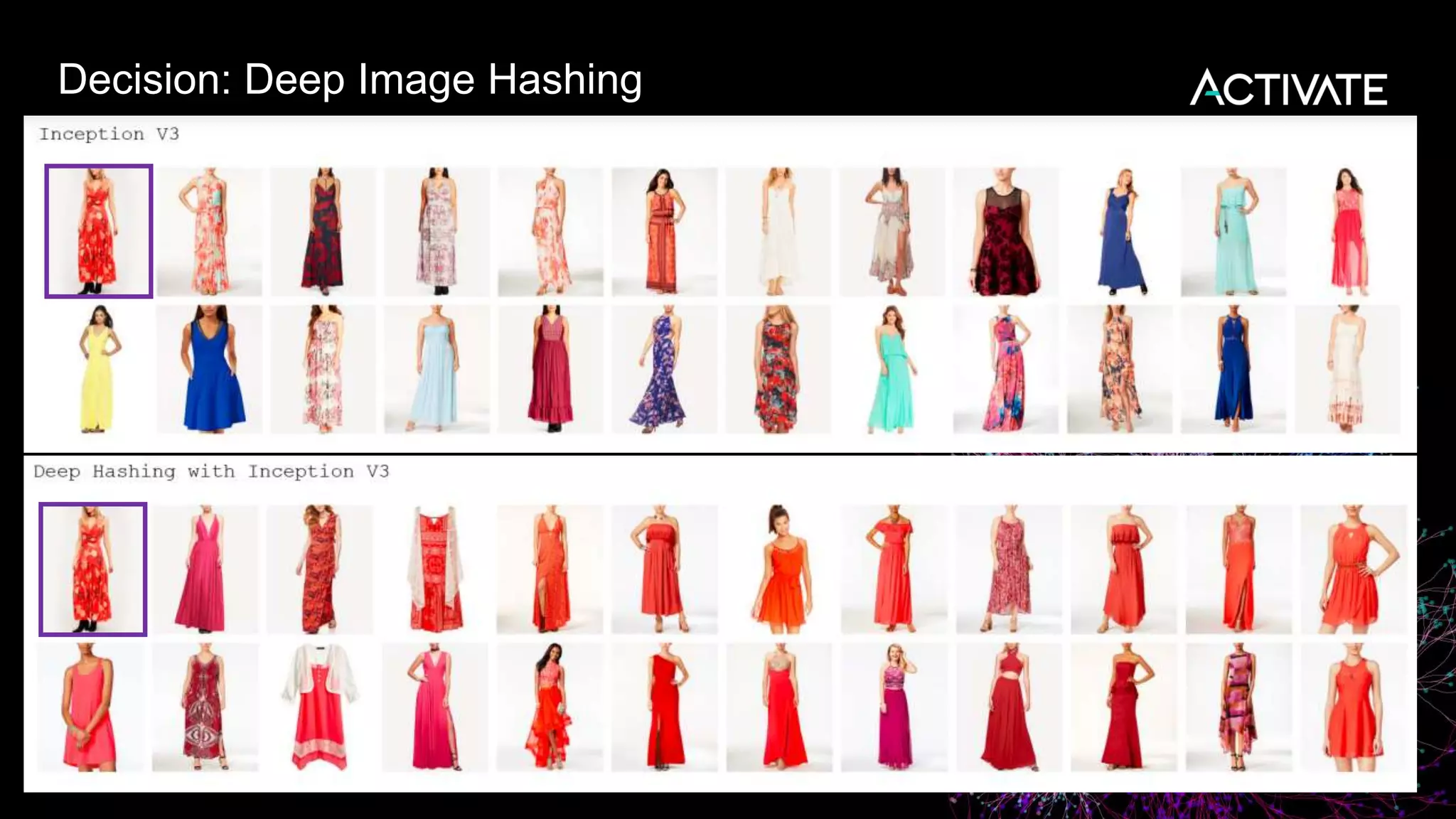
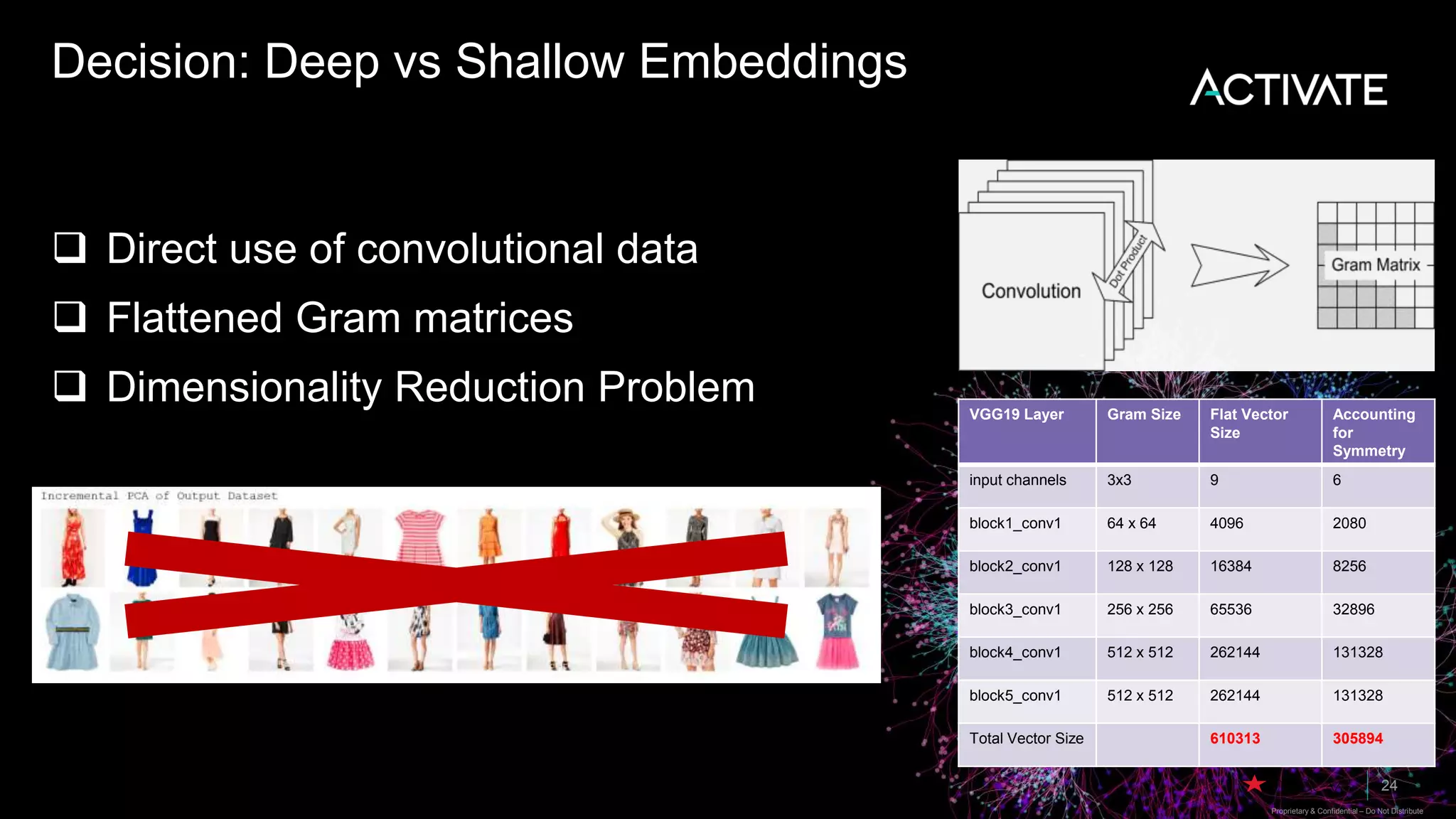
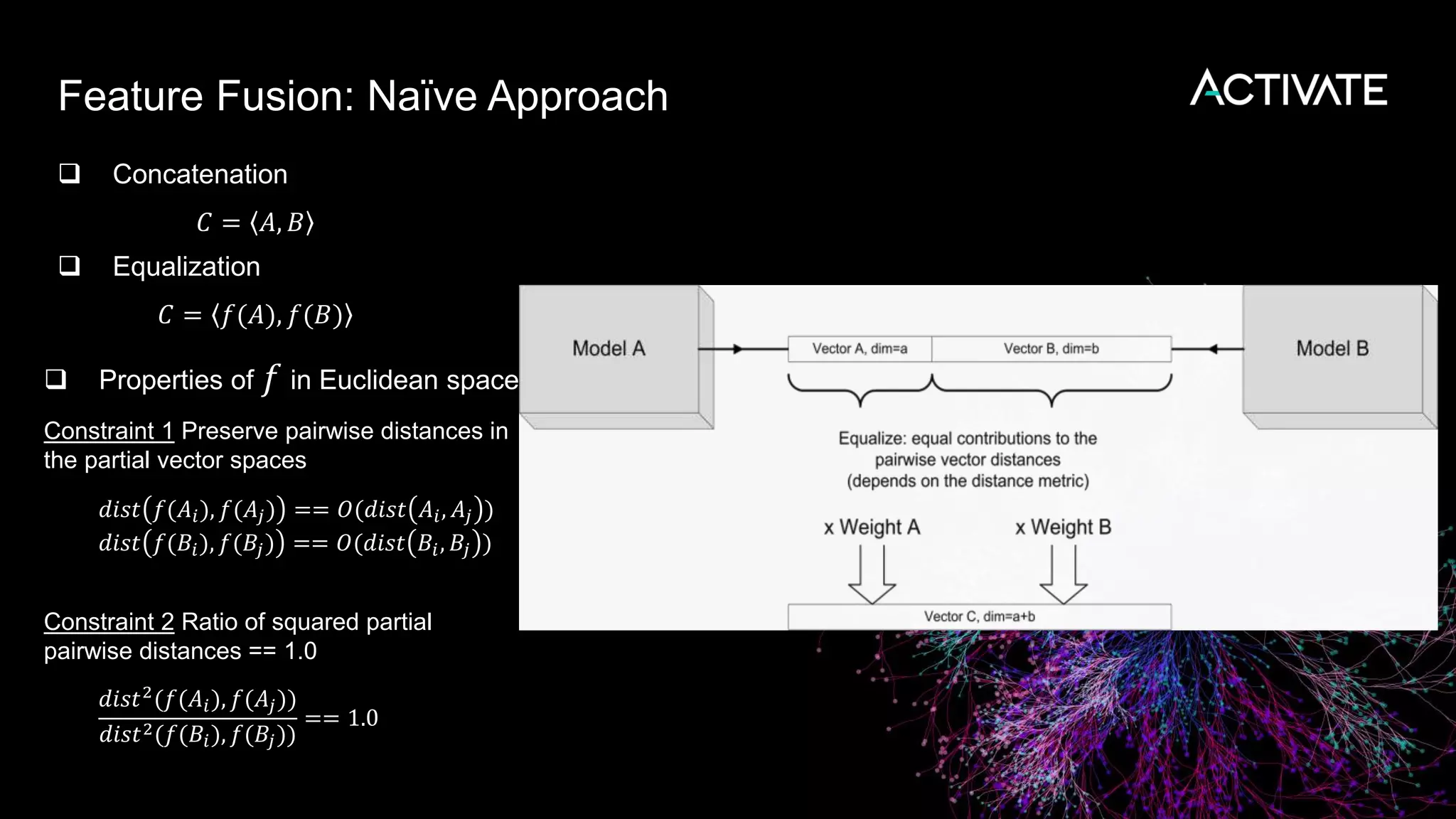
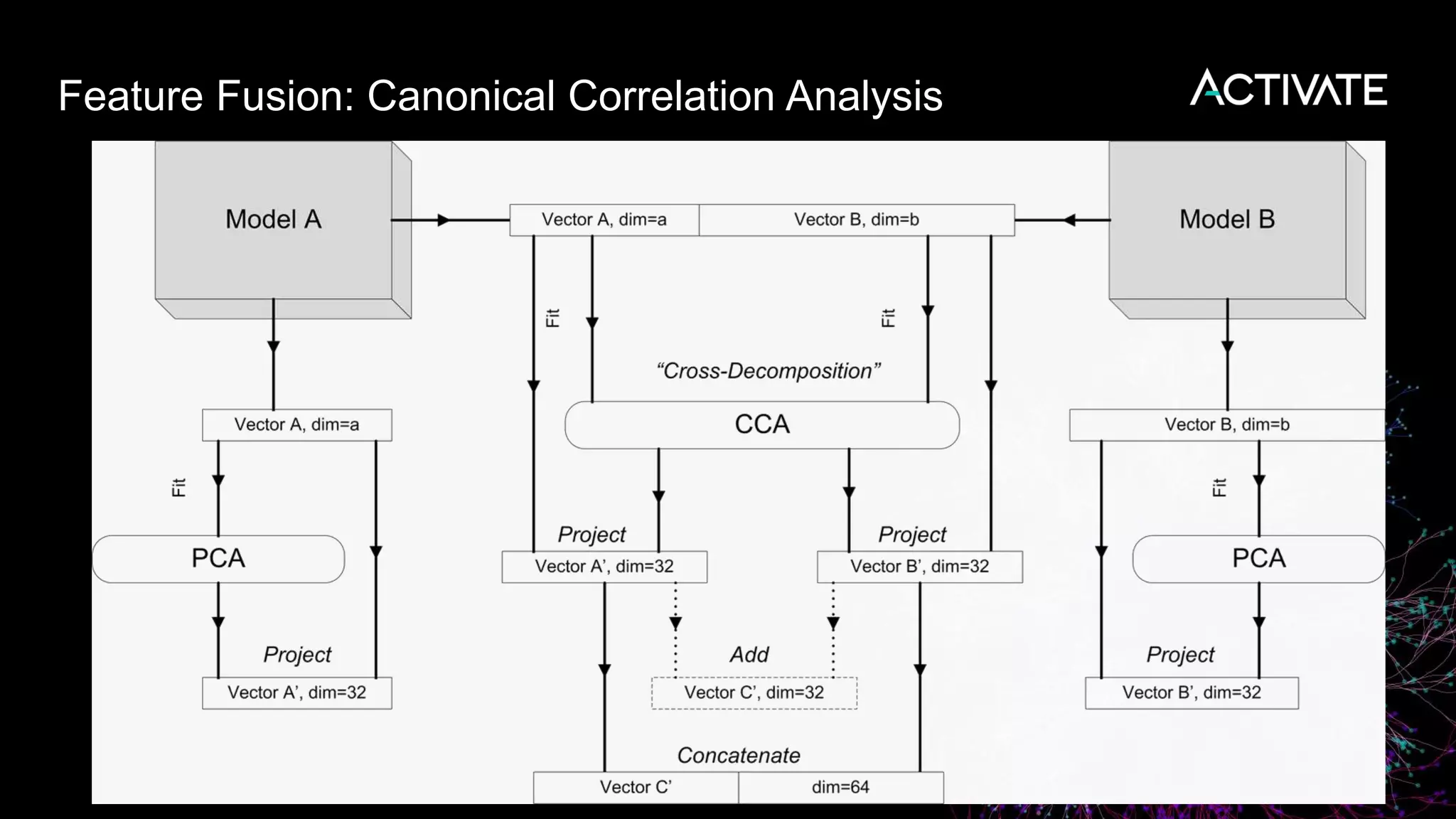
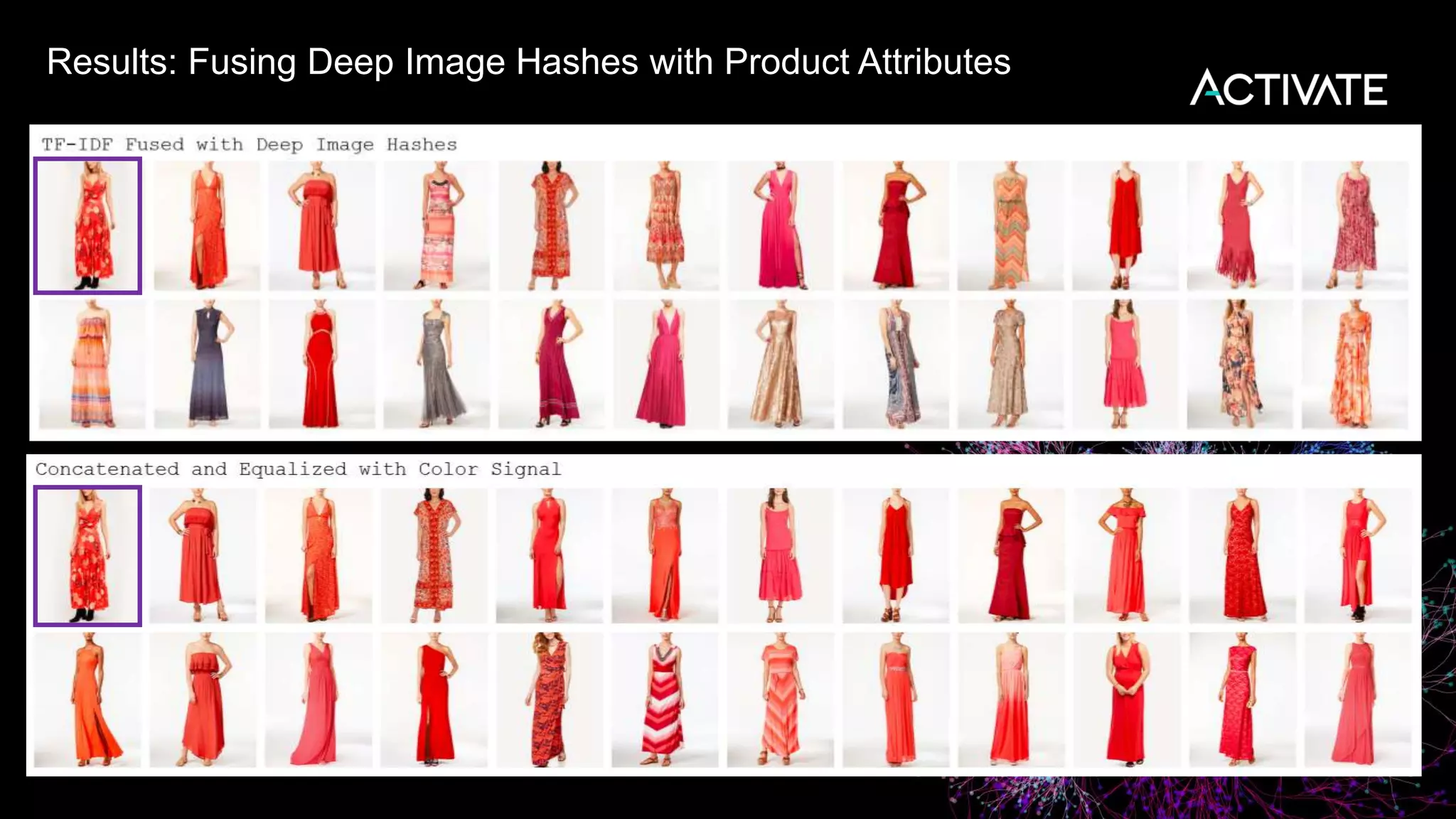
1) Macy's is launching an image-based "More Like This" deep learning feature to provide similar product recommendations to customers on their website. 2) The feature implementation uses transfer learning with pretrained models like MobileNet that are fine-tuned using a triplet loss approach and indexed in Lucene to support fast nearest neighbor search. 3) Engineering decisions around model architecture, embeddings, feature fusion, distance metrics, and indexing were required to deploy the solution at scale for Macy's large product catalog.

1. Image-Based E-Commerce
Product Discovery:
A Deep Learning Case Study
Denis Kamotsky, Peter Gazaryan
@Macys
#Activate18 #ActivateSearch

2. Agenda
• About Macy's
• Where we are with search right now
• 'More Like This' feature overview
• MLT implementation overview
• Transfer Learning and Models Tune Up
• Triple loss approach
• Scoring with vectors similarity metrics in Lucene
• Vector-space retrieval in Lucene

3. 3
Macy’s and macys.com
 1998 Macys.com is launched and operates out of
New York and San Francisco.
 Over 800 locations across the U.S
 2013 Macys.com launches Keyword Search
running on Apache Solr
 Mobile is driving e-commerce growth

4. Image-Based Discovery Use Cases
Visual
Search
Visual
Similarity
Visual
Filtering
Visual
Attribution

5. Visual Search
• Visual Search
• Image Auto-Mapping (Shop the Look)

6. Visual Similarity
• More Like This
• Visual Recommendation Signal

7. Visual Filtering
• Visual Feature Facets
• Likeness Filtering

8. Visual Attribution
• Second Opinion
• New Product Onboarding

9. ‘More Like This’ Feature

10. ‘More Like This’ Feature

11. Serving Model

12. Serving Architecture

13. Spark-Based Pipeline

14. GPU Pipeline: Fast Experimentation

15. Deep Learning Similarity
Train
Retraining
•Fine-Tuning
•Deep Retraining
•Extra Layers
Deep Image
Hashing
Loss
•Classifiers
•Regressors
•Triplet Loss
Vectorize
Models
•Pre-Trained
•Re-Trained
Shallow
Embeddings
Deep Embeddings
Pack
Dimensionality
Reduction
Feature Fusion
Index
Distance Metrics
•Metric Spaces
•Non-Metric Spaces
Indexing Method
•Partitioning
•LSH
•Projections
Search
KNN Search
Radius Search
Exact Methods
Approximate
MethodsDecisions at each
Stage

16. Sample Product: Search by Attributes
 Sample product: red patterned dress
 Attribute vectors: TF-IDF (actually just IDF, because TF==1)
 22615 unique attribute values across catalog subset used in experiments
 Topic Model with 1024 dimensions
 24-NN search results

17. Train and Vectorize

18. Anatomy of a CNN Model

19. Decision: Choose Model Architecture

20. Decision: Deep Image Hashing

21. Decision: Retraining
 Loss
• Classification (multiclass model per attribute, or
multilabel for ease of operations)
• Regression (BOW, TF-IDF, other targets)
• Triplet
 Training Method
• Fine-Tuning
• Deep Retraining
• Extra Layers

22. Example: Triplet Loss Training
Easy Triplet:
Hard Triplet:
Black Box:
MobileNet2
Embedding
Triplet DNN
Anchor
Image
Positive
Image
Negative
Image
Embedding Embedding
Booster
Tower Weights
• Transfer Learning
• Extra Layers
• Custom Loss

23. Results: Re-Training with Triplet Loss

24. 24
Proprietary & Confidential – Do Not Distribute
Decision: Deep vs Shallow Embeddings
VGG19 Layer Gram Size Flat Vector
Size
Accounting
for
Symmetry
input channels 3x3 9 6
block1_conv1 64 x 64 4096 2080
block2_conv1 128 x 128 16384 8256
block3_conv1 256 x 256 65536 32896
block4_conv1 512 x 512 262144 131328
block5_conv1 512 x 512 262144 131328
Total Vector Size 610313 305894
 Direct use of convolutional data
 Flattened Gram matrices
 Dimensionality Reduction Problem

25. Decision: Choosing Convolutional Layers
ReceptiveFieldSize

26. Decision: Choosing Convolutional Layers
ReceptiveFieldSize

27. Pack

28. Feature Fusion: Naïve Approach
 Concatenation
𝐶 = 𝐴, 𝐵
 Equalization
𝐶 = 𝑓(𝐴), 𝑓(𝐵)
 Properties of 𝑓 in Euclidean space
Constraint 1 Preserve pairwise distances in
the partial vector spaces
𝑑𝑖𝑠𝑡 𝑓(𝐴𝑖), 𝑓(𝐴𝑗) == 𝑂(𝑑𝑖𝑠𝑡 𝐴𝑖, 𝐴𝑗 )
𝑑𝑖𝑠𝑡 𝑓(𝐵𝑖), 𝑓(𝐵𝑗) == 𝑂(𝑑𝑖𝑠𝑡 𝐵𝑖, 𝐵𝑗 )
Constraint 2 Ratio of squared partial
pairwise distances == 1.0
𝑑𝑖𝑠𝑡2
(𝑓(𝐴𝑖), 𝑓(𝐴𝑗))
𝑑𝑖𝑠𝑡2(𝑓(𝐵𝑖), 𝑓(𝐵𝑗))
== 1.0

29. Concatenation: Adjusting Color

30. Feature Fusion: Canonical Correlation Analysis

31. Feature Fusion: Deep CCA
• Hyperparameters
• Loss Function
• Target Dimensions
• FC Stack Depth
• Add vs Concatenate Projections
• Performance
• Differentiable Loss
• GPU-Placeable Ops

32. Results: Fusing Deep Embeddings with Product Attributes

33. Results: Fusing Deep Image Hashes with Product Attributes

34. Index

35. Decision: Distance Metric
 Classic: L1 (Manhattan), L2 (Euclidean)
𝑥 1 =
𝑖
𝑥𝑖 ⟹ 𝐿1 𝑥, 𝑦 = 𝑥 − 𝑦 1 =
𝑖
𝑥𝑖 − 𝑦𝑖
𝑥 2 =
𝑖
𝑥𝑖
2
1
2
⟹ 𝐿2 𝑥, 𝑦 = 𝑥 − 𝑦 2 =
𝑖
𝑥𝑖 − 𝑦𝑖
2
1
2
 Fractional Distances: triangle rule is violated
𝐿1
𝑓
𝑥, 𝑦 = 𝑥 − 𝑦 1
𝑓
=
𝑖
𝑥𝑖 − 𝑦𝑖
1
𝑓
𝑓

36. Results: Cosine vs Euclidean
 Cosine distance is a special case of Euclidean distance
𝑐𝑜𝑠_𝑑𝑖𝑠𝑡(𝑥, 𝑦) = 1 − 𝑐𝑜𝑠 𝑥, 𝑦 = 1 −
𝑖 𝑥𝑖 𝑦𝑖
𝑥 2 𝑦 2
=
𝐿2
2 𝑥
𝑥 2
,
𝑦
𝑦 2
2
 Fast to compute for sparse vectors and ranges [0,1] for all-positive vectors  popular in NLP

37. Search

38. KNN Search
 Space Partitioning
 Locality Sensitive Hashing
 Projection to Lower Dimensions
 Scikit-Learn
 Annoy
 NMSLib
 Lucene?!...
Index Type Indexing Time
(including time to
persist raw arrays)
Search
Time
Index Size
(excluding raw
array data size)
Scikit-Learn KD-Tree 100% 100% 100%
Annoy 125% 68% 6%
NMSLib HNSW 395% 68% 6%
NMSLib Brute-Force 51% 85% 0%

39. Conclusion
 Would like arbitrary tensor similarity
signal in the search engine
 When all input tensors are known ahead
of time, results can be pre-computed
 When input tensors are not known
ahead of time, need GPU integration
 Model training pipeline needs to
integrate with indexing pipeline
 Fast KNN search on vectors up to 2048
dimensions is a desirable feature

40. Thank you!
Denis Kamotsky, Peter Gazaryan
@Macys
#Activate18 #ActivateSearch