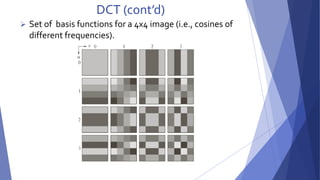
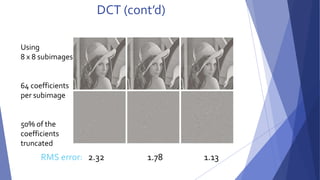
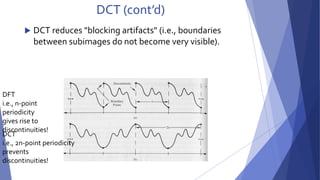
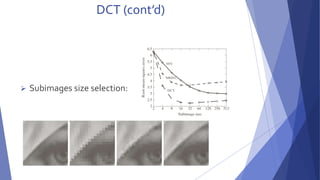
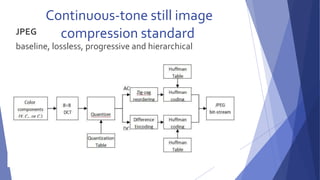
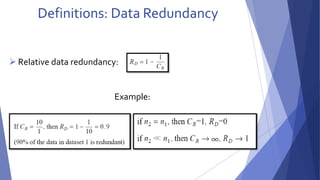
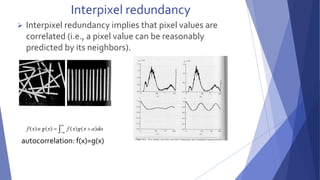
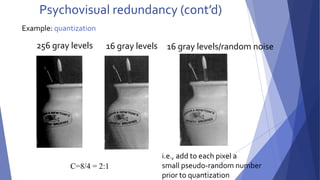
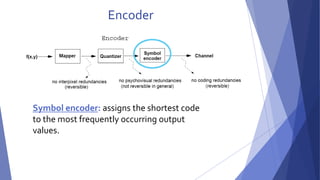
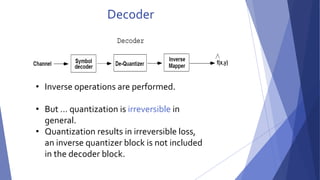
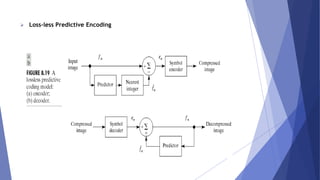
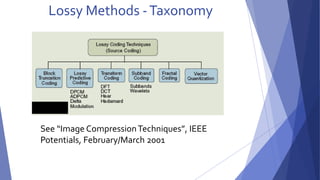
This document summarizes image compression techniques. It discusses: 1) The goal of image compression is to reduce the amount of data required to represent a digital image while preserving as much information as possible. 2) There are three main types of data redundancy in images - coding, interpixel, and psychovisual - and compression aims to reduce one or more of these. 3) Popular lossless compression techniques, like Run Length Encoding and Huffman coding, exploit coding and interpixel redundancies. Lossy techniques introduce controlled loss for further compression.

1. Image Compression
Done By:
Bassam Kanber
Khawla Al-Hashedy
Naglaa Fathi
Redha Qaid
Heba Al-Hakemy
Hesham Al-Aghbary
Supervisor
Ensaf Al-Zurqa

2. Goal of Image Compression
The goal of image compression is to reduce the
amount of data required to represent a digital
image.

3. Data ≠ Information
 Data and information are not synonymous terms!
 Data is the means by which information is conveyed.
 Data compression aims to reduce the amount of data
required to represent a given quantity of information
while preserving as much information as possible.

4. Data vs Information (cont’d)
 The same amount of information can be represented
by various amount of data.
 Ex1:
Your wife, Helen, will meet you at Logan Airport in
Boston at 5 minutes past 6:00 pm tomorrow night
 Ex2:
Your wife will meet you at Logan Airport at 5 minutes
past 6:00 pm tomorrow night
 Ex3:
Helen will meet you at Logan at 6:00 pm tomorrow night

5. Definitions: Compression Ratio
compression
Compression ratio:

6. Definitions: Data Redundancy
 Relative data redundancy:
Example:

7. Types of Data Redundancy
(1) Coding Redundancy
(2) Interpixel Redundancy
(3) Psychovisual Redundancy
 Compression attempts to reduce one or more of these
redundancy types.

8. Coding Redundancy
 Code: a list of symbols (letters, numbers, bits etc.)
 Code word: a sequence of symbols used to represent a
piece of information or an event (e.g., gray levels).
 Code word length: number of symbols in each code
word

9. Coding Redundancy (cont’d)
N x M image
rk: k-th gray level
P(rk): probability of rk
l(rk): # of bits for rk
Expected value:

10. Coding Redundancy (con’d)
Case 1: l(rk) = constant length
Example:

11. Case 2: l(rk) = variable length

12. Interpixel redundancy
 Interpixel redundancy implies that pixel values are
correlated (i.e., a pixel value can be reasonably
predicted by its neighbors).
autocorrelation: f(x)=g(x)

13. Interpixel redundancy (cont’d)
 To reduce interpixel redundancy, the data must be
transformed in another format (i.e., using a transformation)
 e.g., thresholding, DFT, DWT, etc.
 Example:
origin
al
thresholded

14. Psychovisual redundancy
 The human eye does not respond with equal sensitivity
to all visual information.
 It is more sensitive to the lower frequencies than to the
higher frequencies in the visual spectrum.
 Idea: discard data that is perceptually insignificant!

15. Psychovisual redundancy (cont’d)
256 gray levels 16 gray levels 16 gray levels/random noise
C=8/4 = 2:1
i.e., add to each pixel a
small pseudo-random number
prior to quantization
Example: quantization

16. Fidelity Criteria
 How close is to ?
 Criteria
 Subjective: based on human observers
 Objective: mathematically defined criteria

17. Subjective Fidelity Criteria

18. Objective Fidelity Criteria
 Root mean square error (RMS)
 Mean-square signal-to-noise ratio (SNR)

19. Objective Fidelity Criteria (cont’d)
RMSE = 5.17 RMSE = 15.67 RMSE = 14.17

20. Image Compression Models
 The image compression system is composed of 2
distinct structural blocks: an encoder & a decoder.
 Encoder performs Compression
 Decoder performs Decompression.

21.  The encoder is made up of a source encoder which removes
input redundancies, and a channel encoder, which increases the
noise immunity of the source encoder's output.
 The de-coder includes a channel decoder followed by a source
decoder.

 If the channel between the encoder and decoder is noise free (no
prone or error) the channel encoder and decoder are omitted.
 Input image f(x,y) is fed into the encoder, which creates a
compressed representation of input.
 It is stored for future for later use or transmitted for storage and
use at a remote location.
 When the compressed image is given to decoder, a reconstructed
output image f’(x,…..) is generated.
 The encoded input and decoder output are f(x, y) & f’(x, y) resp.
 In video applications, they are f(x, y, t) & f’(x, y, t) where t is time.

22.  1-The Source Encoder and Decoder::
 The source encoder is responsible for reducing or eliminating any
coding, interpixel and psychovisual redundancies in the input
image.
 Encoder is used to remove the redundancies through a series of 3
independent operations.
 Mapper:It transforms f(x,y) into a format designed to reduce
interpixel redundancies.
 It is reversible
 It may / may not reduce the amount of data to represent image.
 Ex. Run Length coding
 Quantizer: reduces the accuracy of the mapper's output in
accordance with some pre-established fidelity criterion. This stage
reduces the psychovisual redundancies of the input image.
 This operation is irreversible.

23. Encoder
 Symbol Encoder: Generates a fixed or variable length
code to represent the quantizer output and maps the
output in accordance with the code.
• In most cases, a variable-length code is used to represent
the mapped and quantized data set. It assigns the shortest
code words to the most frequently occurring output values
and thus reduces coding redundancy.
• It is reversible.
• Upon its completion, the input image has been processed
for the removal of all 3 redundancies.

24. Encoder
Mapper: transforms input data in a way
that facilitates reduction of interpixel
redundancies.

25. Encoder
Quantizer: reduces the accuracy of the
mapper’s output in accordance with some pre-established
fidelity criteria.

26. Encoder
Symbol encoder: assigns the shortest code
to the most frequently occurring output
values.

27. Decoder
• Inverse operations are performed.
• But … quantization is irreversible in
general.
• Quantization results in irreversible loss,
an inverse quantizer block is not included
in the decoder block.

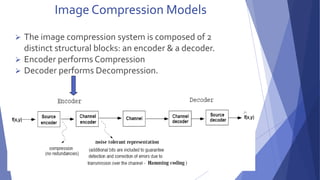
29. Channel
 2-The Channel Encoder and Decoder::
 In the overall encoding-decoding process when the channel is noisy or
prone to error They are designed to reduce the impact of channel noise by
inserting a controlled form of redundancy into the source encoded data.
 As the output of the source encoder contains little redundancy, it would
be highly sensitive to transmission noise without the addition of this
"controlled redundancy."
 One of the most useful channel encoding techniques was devised by R.
W.Hamming (Hamming [1950]).
 It is based on appending enough bits to the data being encoded to ensure
that some minimum number of bits must change between valid code
words.
 Hamming(7,4) is a linear error-correcting code that encodes 4 bits of data
into 7 bits by adding 3 parity bits.
 Hamming's (7,4) algorithm can correct any single-bit error, or detect all
single-bit and two-bit errors.

30. Elements of Information Theory
 Measuring Information
 The generation of information is modeled as a probabilistic
process. Random event E occurs with probability P(E)
 I(E)=log= 1 =_ log (p(E))
 P(E)
 The base of the logarithm determines the units used to measure
the information. If the base 2 is selected the resulting
information unit is called bit. If P(E)=0.5 (two possible equally
likely events) the information is one bit
 I(E) is called the self-information of E.

31. The Information Channel
Information channel is the physical medium that
connectsthe information source to the user of information.
Self-information is transferred between an information
source and a user of the information, through the
information channel.
Information source
Generates a random sequence of symbols from a finite or
countably infinite set of possible symbols.
Output of the source is a discrete random variable

32.  The source :
Modeled as a discrete random variable
Source alphabet A={aj}
Symbols (letters) aj with probabilities P(aj)

33. A simple information system
Output of the channel is also a discrete random variable which
takes on values from a finite or countably infinite set of symbols
{b1, b2,…, b K} called the channel alphabet B

34. Entropy
Conditional entropy function
units/pixel

35. Entropy Estimation
It is not easy to estimate H reliably!
image

36. Entropy
First order estimate of H:

37. Entropy
Second order estimate of H:
Use relative frequencies of pixel blocks

38. Estimating Entropy
The first-order estimate provides only a lower-bound on
the compression that can be achieved.
Differences between higher-order estimates of entropy
and the first-order estimate indicate the presence of
interpixel redundancy!

39. Estimating Entropy
For example, consider differences:
16

40. Estimating Entropy
 Entropy of difference image:
 Better than before (i.e., H=1.81 for original image)
 However, a better transformation could be found
since:

41. Compression Types
Compression
Error-Free
Compression
(Loss-less)
Lossy
Compression

42. Error-Free Compression
 Some applications require no error in compression
(medical, business documents, etc..)
 CR=2 to 10 can be expected.
 Make use of coding redundancy and inter-pixel
redundancy.
 Ex: Huffman codes, LZW, Arithmetic coding, 1D and 2D
run-length encoding, Loss-less Predictive Coding, and
Bit-Plane Coding.

43. Run-length encoding (RLE)
 is a very simple form of data compression
 stored as a single data value and count.
 Ex: AAAABBCCCAA
Sol: 3A2B3C2A

44. Huffman Coding
 Huffman Coding
 The most popular technique for removing coding
redundancy is due to Huffman (1952)
 A variable-length coding technique.
 Optimal code (i.e., minimizes the number of code
symbols per source symbol).
 Huffman Coding yields the smallest number of code
symbols per source symbol
 Assumption: symbols are encoded one at a time!

45. Huffman Coding

46. Huffman Coding
1(0.4) 2(0.3) 3(0.1) 4(0.1) 5(0.06) 5(0.04)
bits
Lavg
2.2

     

47.  Arithmetic coding
 5 symbol message, a1a2a3a3a4 from 4 symbol
source is coded.
Source Symbol Probability Initial Subinterval
a1 0.2 [0.0, 0.2)
a2 0.2 [0.2, 0.4)
a3 0.4 [0.4, 0.8)
a4 0.2 [0.8, 1.0)

48. Arithmetic coding

49.  The final message symbol narrows to [0.06752,
0.0688).
 Any number between this interval can be used to
represent the message.
 E.g. 0.068
 3 decimal digits are used to represent the 5 symbol
message.

50. Fixed Length: LZW Coding
 Error Free Compression Technique
 Remove Inter-pixel redundancy
 Requires no priori knowledge of probability
distribution of pixels
 Assigns fixed length code words to variable length
sequences
 Patented Algorithm US 4,558,302
 Included in GIF and TIFF and PDF file formats

51. Coding Technique
 A codebook or a dictionary has to be constructed
 For an 8-bit monochrome image, the first 256
entries are assigned to the gray levels 0,1,2,..,255.
 As the encoder examines image pixels, gray level
sequences that are not in the dictionary are
assigned to a new entry.
 For instance sequence 255-255 can be assigned to
entry 256, the address following the locations
reserved for gray levels 0 to 255.

52. Example
Consider the following 4 x 4 8 bit image
39 39 126 126
39 39 126 126
39 39 126 126
39 39 126 126
Dictionary Location Entry
0 0
1 1
. .
255 255
256 -
511 -

53. 39 39 126 126
39 39 126 126
39 39 126 126
39 39 126 126
• Is 39 in the
dictionary……..Yes
• What about 39-
39………….No
• Then add 39-39 in entry 256
• And output the last
recognized symbol…39
Dictionary Location Entry
0 0
1 1
. .
255 255
256 39-39
511 -

54. Bit-Plane Coding
 An effective technique to reduce inter pixel
redundancy is to process each bit plane
individually
 The image is decomposed into a series of binary
images.
 Each binary image is compressed using one of
well known binary compression techniques.

55. Bit-Plane Decomposition

56. Bit-Plane Encoding
 one Dimensional Run Length coding
 Two Dimensional Run Length coding

57.  Loss-less Predictive Encoding

59. Decoding LZW
 Use the dictionary for decoding the “encoded output”
sequence.
 The dictionary need not be sent with the encoded
output.
 Can be built on the “fly” by the decoder as it reads the
received code words.

60. Run-length coding (RLC)
(interpixel redundancy)
 Encodes repeating string of symbols (i.e., runs) using
a few bytes: (symbol, count)
1 1 1 1 1 0 0 0 0 0 0 1  (1,5) (0, 6) (1, 1)
a a a b b b b b b c c  (a,3) (b, 6) (c, 2)
 Can compress any type of data but cannot achieve
high compression ratios compared to other
compression methods.

61. Bit-plane coding (interpixel
redundancy)
 Process each bit plane individually.
 (1) Decompose an image into a series of binary images.
 (2) Compress each binary image (e.g., using run-length
coding)

62. Combining Huffman Coding
with Run-length Coding
 Assuming that a message has been encoded using
Huffman coding, additional compression can be
achieved using run-length coding.
e.g., (0,1)(1,1)(0,1)(1,0)(0,2)(1,4)(0,2)

63. Lossy Methods -Taxonomy
See “Image Compression Techniques”, IEEE
Potentials, February/March 2001

64. Lossy Compression
 Transform the image into a domain where
compression can be performed more efficiently (i.e.,
reduce interpixel redundancies).
~ (N/n)2 subimages

65. Transform Selection
 T(u,v) can be computed using various
transformations, for example:
DFT
DCT (Discrete Cosine Transform)
KLT (Karhunen-Loeve Transformation)

66. Example: Fourier Transform
The magnitude
of the FT
decreases, as u,
v increase! K << N

67. DCT (Discrete Cosine Transform)
Forward
Inverse

68. DCT (cont’d)
 Set of basis functions for a 4x4 image (i.e., cosines of
different frequencies).

69. DCT (cont’d)
Using
8 x 8 subimages
64 coefficients
per subimage
50% of the
coefficients
truncated
RMS error: 2.32 1.78 1.13

70. DCT (cont’d)
 DCT reduces "blocking artifacts" (i.e., boundaries
between subimages do not become very visible).

71. DCT (cont’d)
 DCT reduces "blocking artifacts" (i.e., boundaries
between subimages do not become very visible).
DFT
i.e., n-point
periodicity
gives rise to
discontinuities!
DCT
i.e., 2n-point periodicity
prevents
discontinuities!

72. DCT (cont’d)
 Subimages size selection:

73. image compression standard
 ISO & CCITT
 Binary
 Continuous-tone
 Video

74. Binary image compression
 Fax: standard
-Transmitting Docs. over Tele. Nets.
 CCITT Group 3 (Huffman) 1D & 2D
 CCITT Group 4 2D
 JBIG 1

75. Continuous-tone still image
JPEG compression standard
baseline, lossless, progressive and hierarchical

76. JPEG 2000
 wavelet and sub-band technologies
 Embedded Block Coding with Optimized
Truncation (EBCOT)

77. Features of JPEG2000
 Lossless and lossy compression.
 Protective image security.
 Region-of-interest coding.
 Robustness to bit errors.

78. JPEG-LS
 latest ISO/ITU-T standard for lossless coding of still
images.
 provides for “near-lossless” compression.
 Part-I:
the baseline system, is based on:
adaptive prediction, context modeling and Golomb
coding.
 Part-II (still under preparation).
 Designed for low-complexity.

79. Video Compression Standards
 MPEG-1
The driving focus of the standard was storage of multimedia
content on a standard CDROM, which supported data
transfer rates of 1.4 Mb/s and a total storage capability of
about 600 MB.
 MPEG-2
Designed to provide the capability for compressing, coding,
and transmitting high quality, multi-channel, multimedia
signals over broadband networks.
ex: ATM.
 MPEG-4
Digital television, interactive graphics and the World Wide
Web.