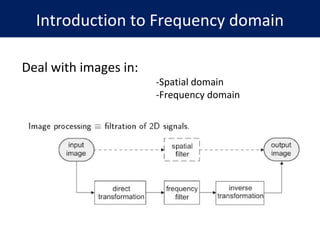
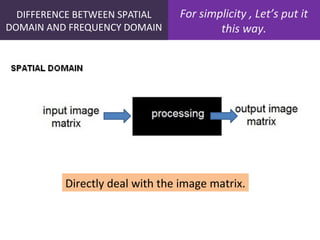
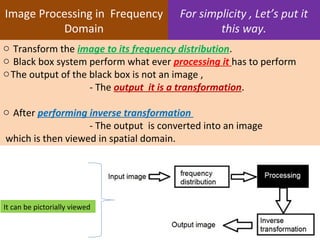
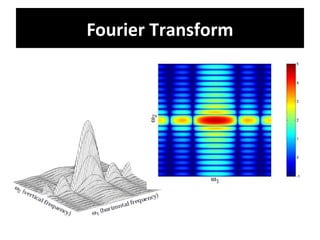
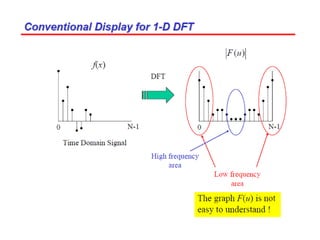
1. The document discusses image processing in the frequency domain, which involves transforming an image into its frequency distribution using mathematical operators called transformations like the Fourier transform. 2. The Fourier transform decomposes an image into its frequency components, which can be divided into high frequency components corresponding to edges and low frequency components corresponding to smooth regions. 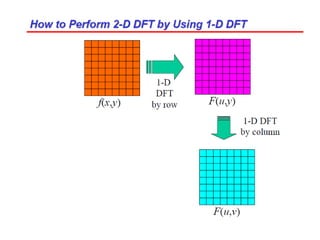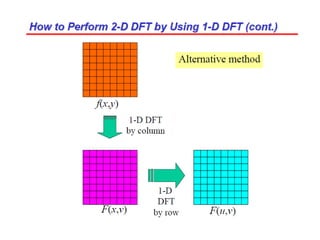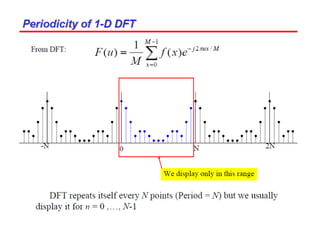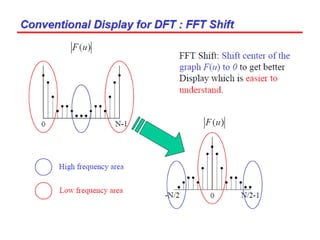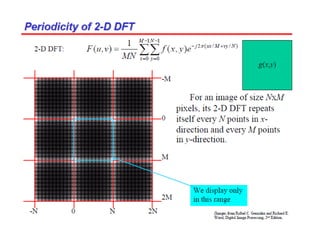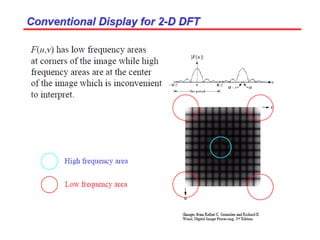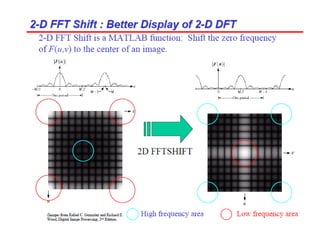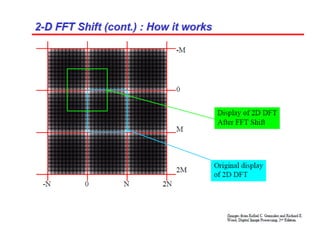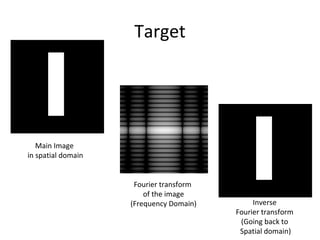3. An example computes the 2D discrete Fourier transform of a toy image using zero-padding to increase resolution, and the fftshift function is used to center the DC coefficient when visualizing the transformed image.

1. Image processing in frequency Domain
Department of Computer Science And Engineering
Shahjalal University of Science and Technology
Nashid Alam
Registration No: 2012321028
annanya_cse@yahoo.co.uk
Masters -2 Presentation
(Backup Slides# 6)

2. Introduction to Frequency domain
Deal with images in:
-Spatial domain
-Frequency domain

3. Difference between spatial domain and frequency domain
Spatial domain :
- Deal with images as it is.
- The value of the pixels of the image
change with respect to scene.
Frequency domain :
-Deal with the rate at which
the pixel values are changing in spatial
domain.

4. For simplicity , Let’s put it
this way.
DIFFERENCE BETWEEN SPATIAL
DOMAIN AND FREQUENCY DOMAIN
Directly deal with the image matrix.

5. For simplicity , Let’s put it
this way.
Image Processing in Frequency
Domain
o Transform the image to its frequency distribution.
o Black box system perform what ever processing it has to perform
oThe output of the black box is not an image ,
- The output it is a transformation.
o After performing inverse transformation
- The output is converted into an image
which is then viewed in spatial domain.
It can be pictorially viewed

6. Frequency Components
Any image in spatial domain can be represented
in a frequency domain.
But what do this frequencies actually mean?
Frequency components are divided into two major components.
1. HIGH FREQUENCY COMPONENTS
High frequency components correspond to edges in an image.
2. LOW FREQUENCY COMPONENTS
Low frequency components in an image correspond to smooth regions.

7. TRANSFORMATION
Transformation:
A signal can be converted from spatial domain
into frequency domain using mathematical operators called
transformation.
kind of transformation:
Fourier Series
Fourier transformation
Laplace transform
Z transform

8. Fourier Transform

9. Fourier Transform
f(m, n) is a function of two discrete spatial variables m and n,
Two-dimensional Fourier transform of f(m, n) :
The variables ω1 and ω2 are frequency variables
ω1 and ω2 both are periodic with period 2π
Where, -2π<= ω1 and 2π<= ω2
F(ω1,ω2 ) is often
called the
frequency-domain
representation of
f(m, n)

10. Fourier Transform
F(0,0 ) is the sum of all the values of f(m, n)
F(0,0 ) is often called the constant component or
DC component of the Fourier transform.
(DC stands for direct current:
It is an electrical engineering term that refers to a constant-voltage power source, as
opposed to a power source whose voltage varies sinusoidally.)
frequency-domain representation of f(m, n):

11. Fourier Transform
The inverse two-dimensional Fourier transform is given by:
This equation means that f(m, n) can be represented as:
A sum of an infinite number of
complex exponentials (sinusoids)
with different frequencies.

12. Example2D Fourier Transform
Consider a function f(m, n) :
1 within a rectangular region
0 everywhere else.
To simplify the diagram:
f(m, n) is shown as a continuous function, even
though the variables m and n are discrete

13. Example2D Fourier Transform
The magnitude of the Fourier transform, |F(ω1,ω2 )| is shown in mesh plot.

14. This reflects the fact:
-Horizontal cross sections of are narrow pulses,
vertical cross sections are broad pulses.
-Narrow pulses have more high-frequency
content than broad pulses.
Example2D Fourier Transform
The plot also shows :
More energy at high horizontal frequencies
Less energy at high vertical frequencies.
Example Of How To Do This
Is In Next Slide

31. Implemented example

32. Example
Relationship to 2D Fourier
transform with spatial image
Construct a matrix f that is similar to the function f(m, n)
f = zeros(30,30);
f(5:24,13:17) = 1;
imshow(f,'notruesize')
(b) Main Image
(Toy image Constriction)
in spatial domain
(c)Fourier transform of the
image(Frequency Domain)
(a) Toy Image

33. Example2D Fourier Transform
Main Image
in spatial domain
Orthogonal
Compute and visualize
the 30-by-30 DFT of f(m,n)

34. Target
Main Image
in spatial domain
Fourier transform
of the image
(Frequency Domain) Inverse
Fourier transform
(Going back to
Spatial domain)

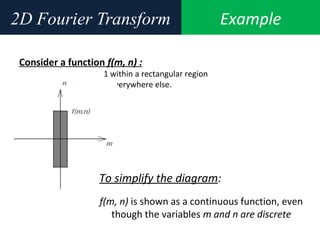
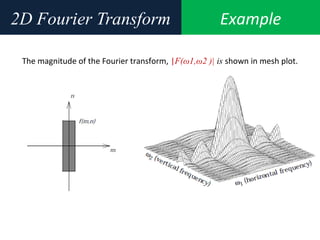
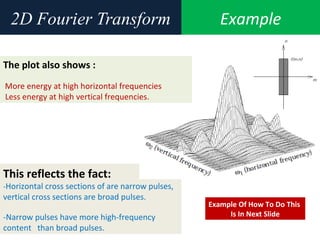
35. Example2D Fourier Transform
Compute and visualize the 30-by-30 DFT of f(m,n)
F = fft2(f);
F2 = log(abs(F));
imshow(F2,[-1 5],'notruesize');
%% colormap(jet); colorbar

36. Example2D Fourier Transform
Doesn’t match
the target Fourier Transformed Image
The resolution is much lower
DC coefficient of F(0,0) is displayed
in the upper-left corner instead of
the traditional location in the center
(b) Target Fourier Transformed Image
(b) Visualize the 30-by-30 DFT
F(0,0) value is called DC coefficients
DC=Direct Current

37. Example2D Fourier Transform
The resolution is increased
by zero-padding f when computing its DFT.
Need more computation
%resolution is increased by zero-padding f
%zero-pads f to be 256-by-256 before
%computing the DFT
F = fft2(f,256,256);
Dealing with Resolution

38. Example2D Fourier Transform
DCT coefficients of Fourier transform are displayed much more finely
The result is :
(a) DCT result Before zero-padding (b) DCT result After zero-padding
(fine result)
Need more computation Dealing with Resolution
F = fft2(f,256,256);

39. Example2D Fourier Transform
Need more computation Dealing with displaying DC coefficient of F(0,0)
fix this problem by using the function fftshift,
which swaps the quadrants of F so that the DC
coefficient is in the center.
imshow(log(abs(F)),[-1 5]);
(b) Target Fourier Transformed Image

40. Example2D Fourier Transform
compute the inverse DFT
(a) Fourier transform
of the image
(Frequency Domain)
(b) Inverse
Fourier transform
(Going back to
Spatial domain)