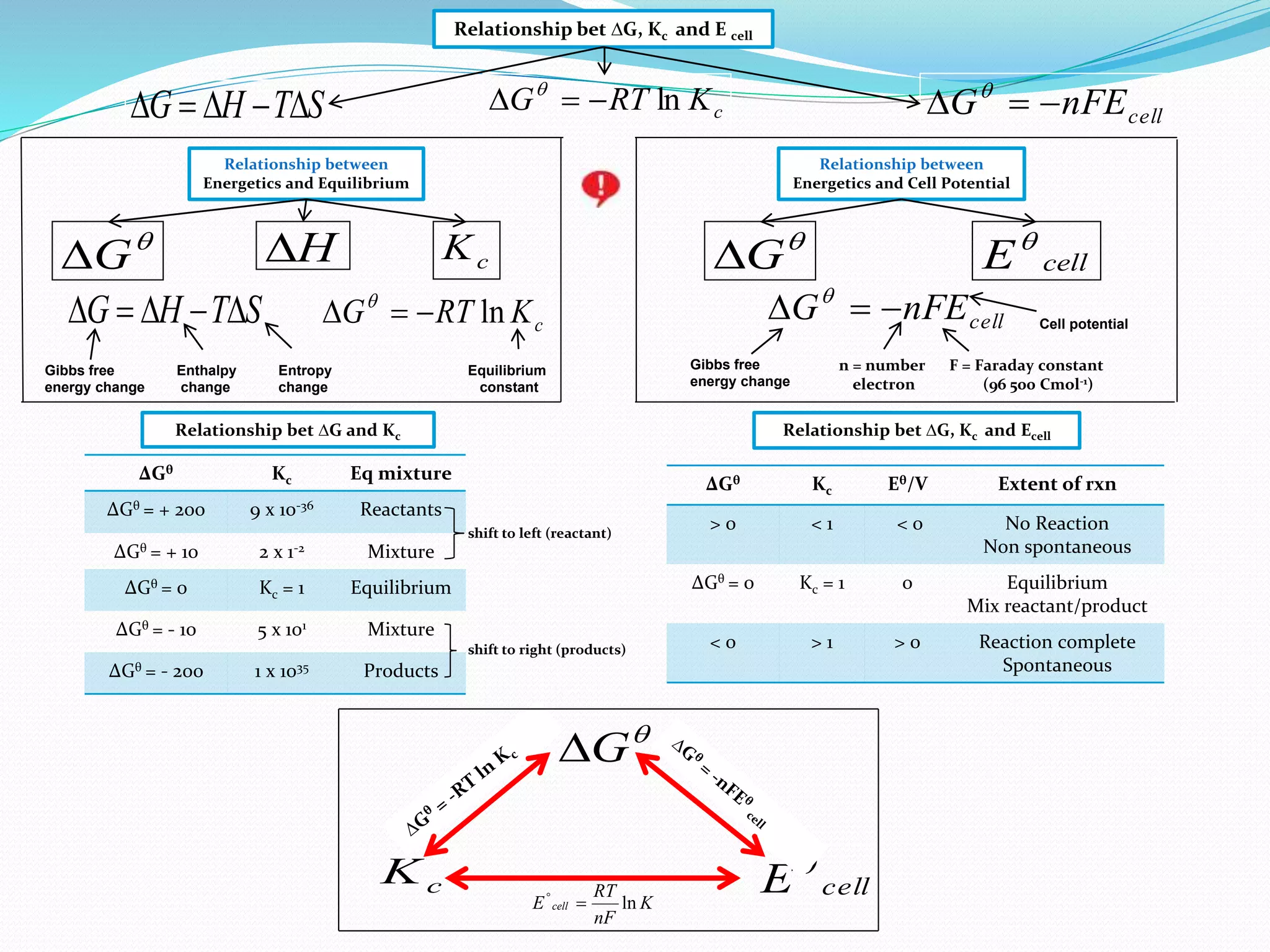
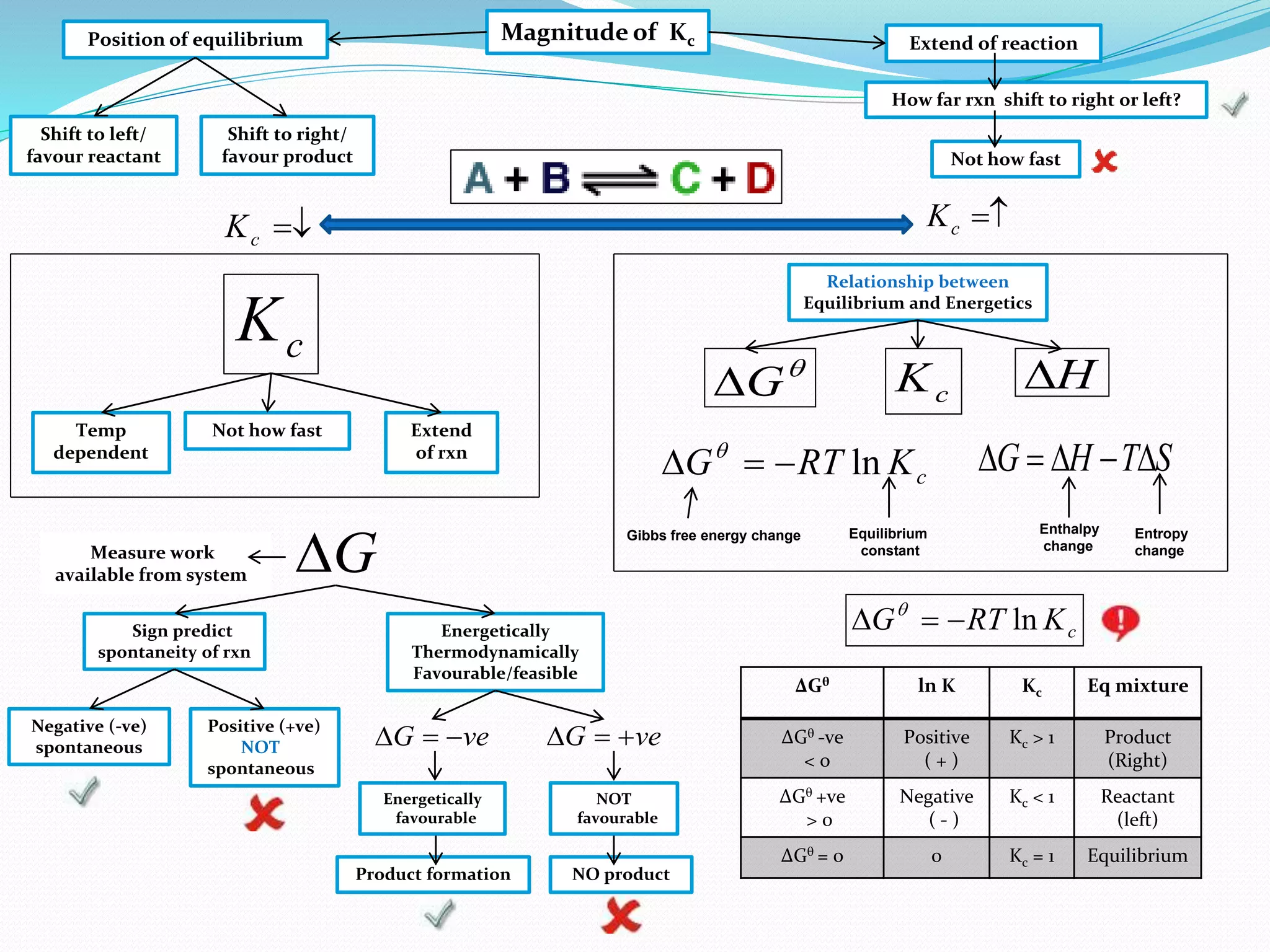
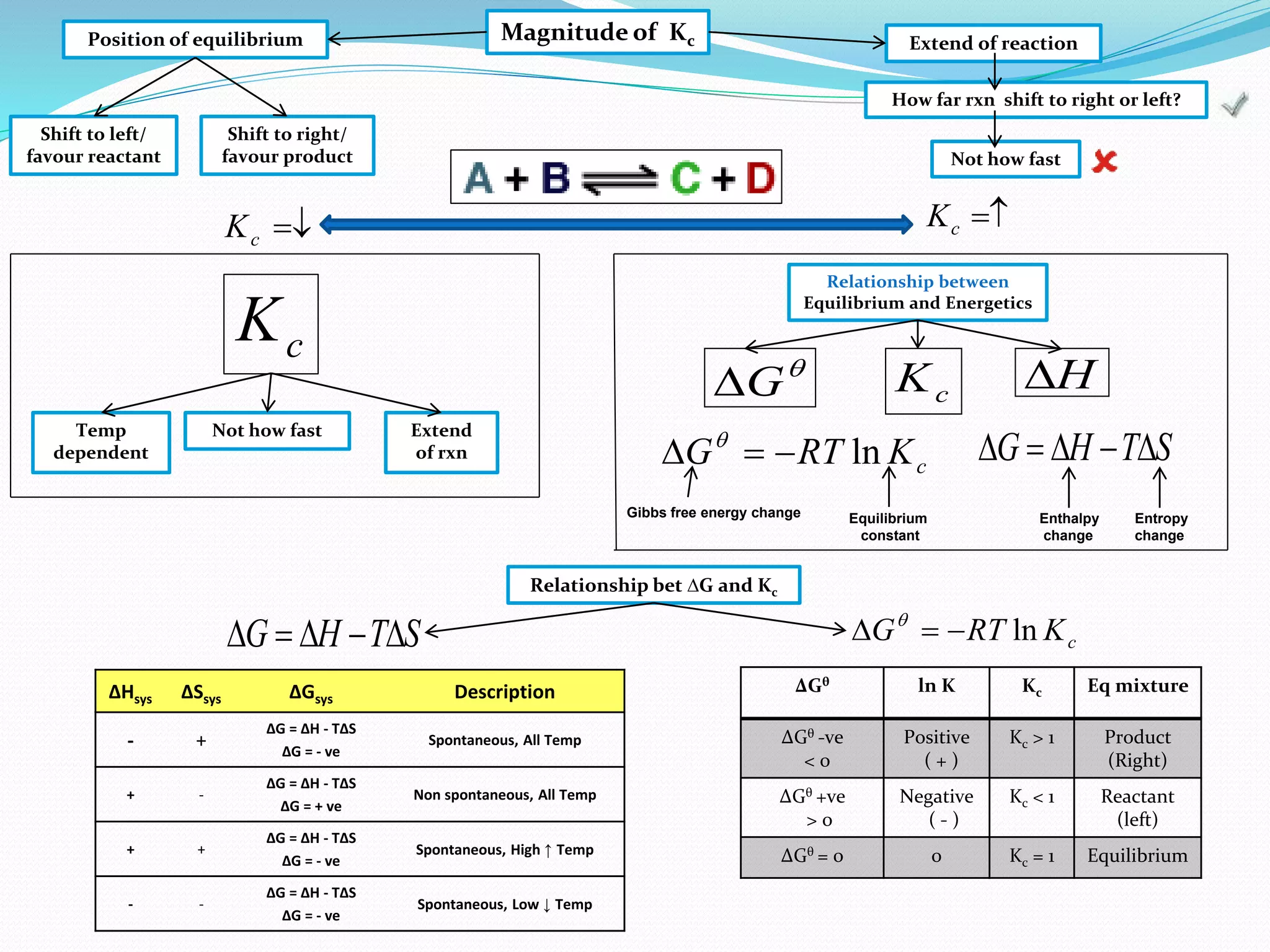
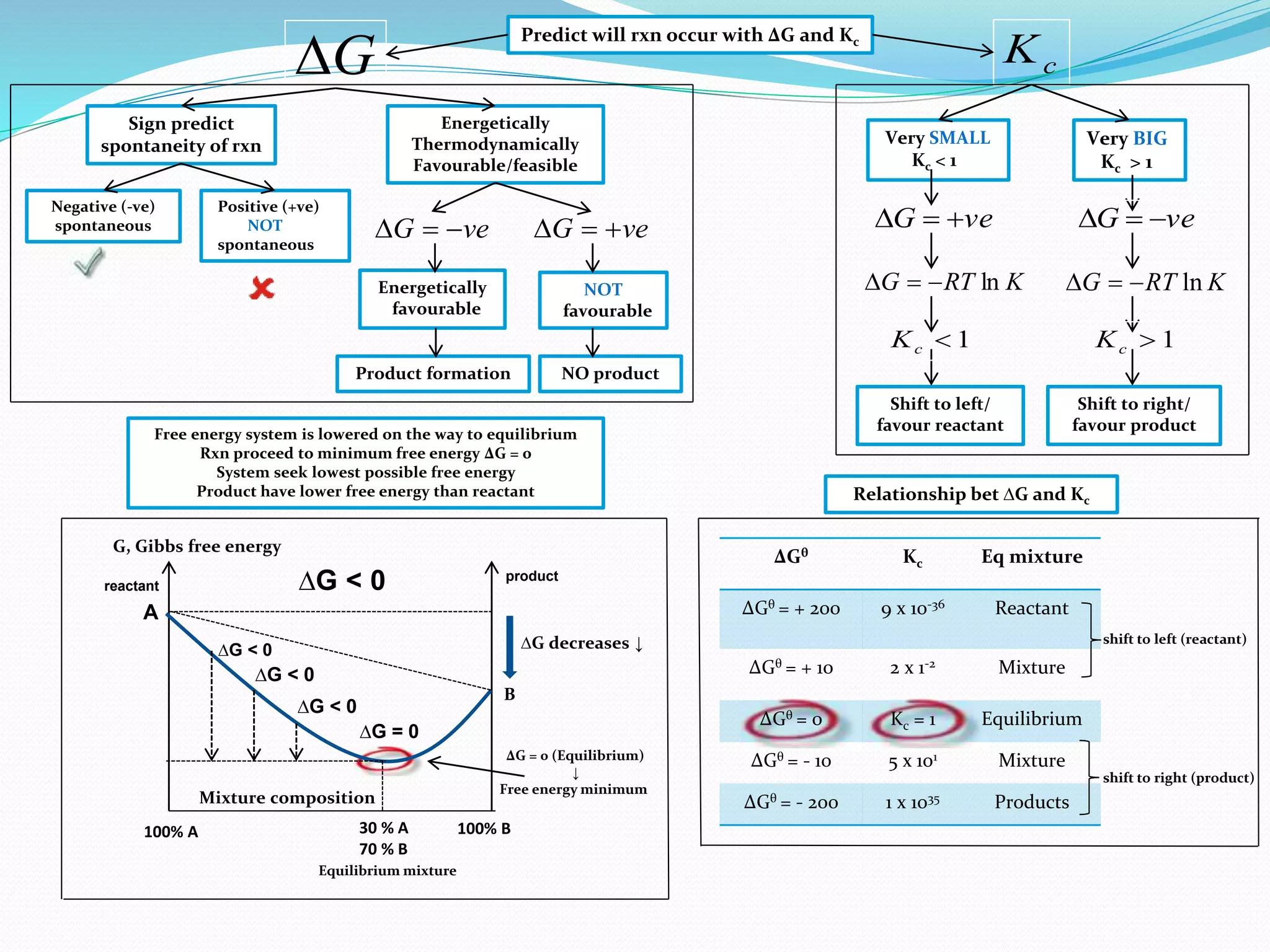
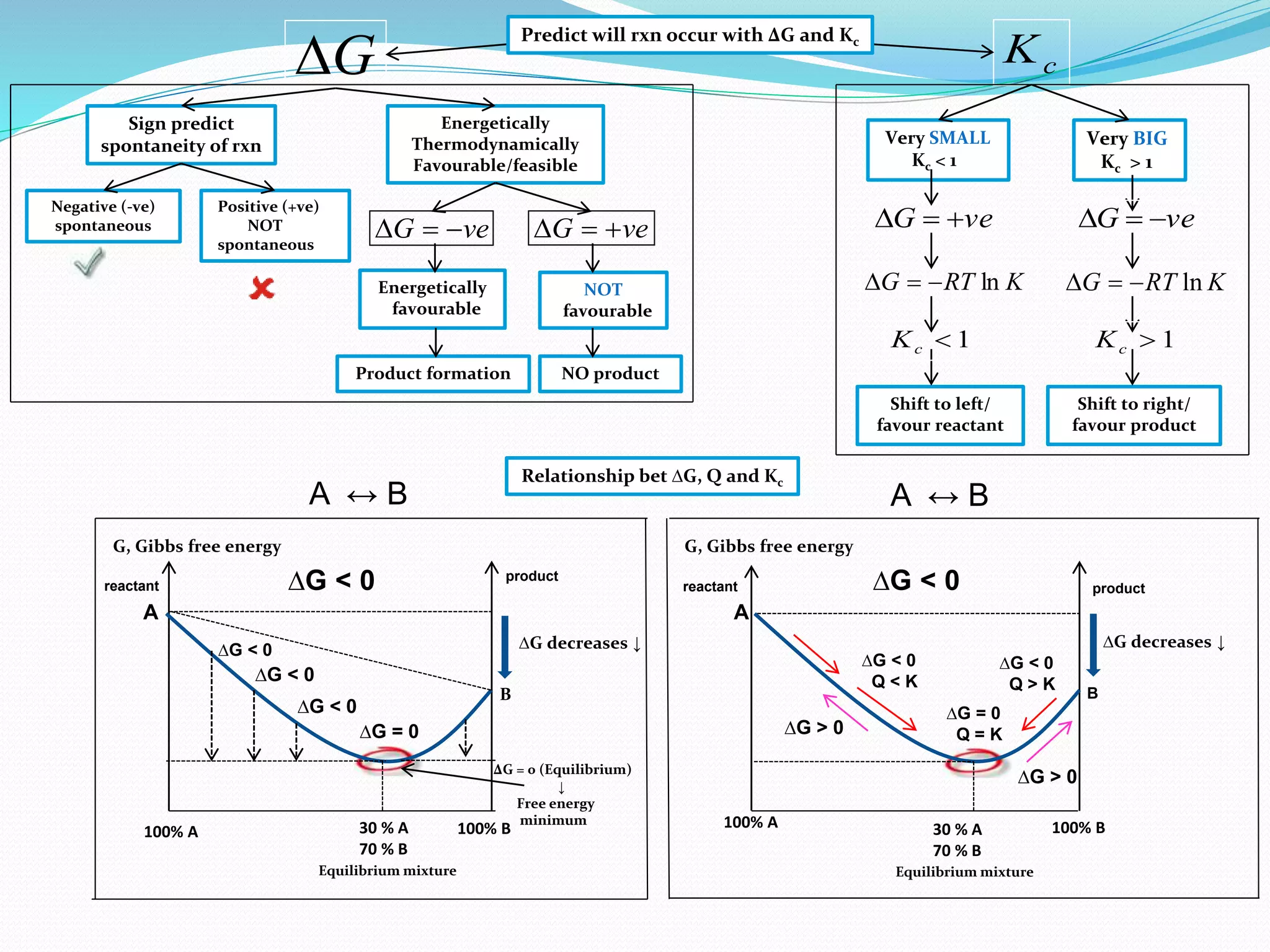
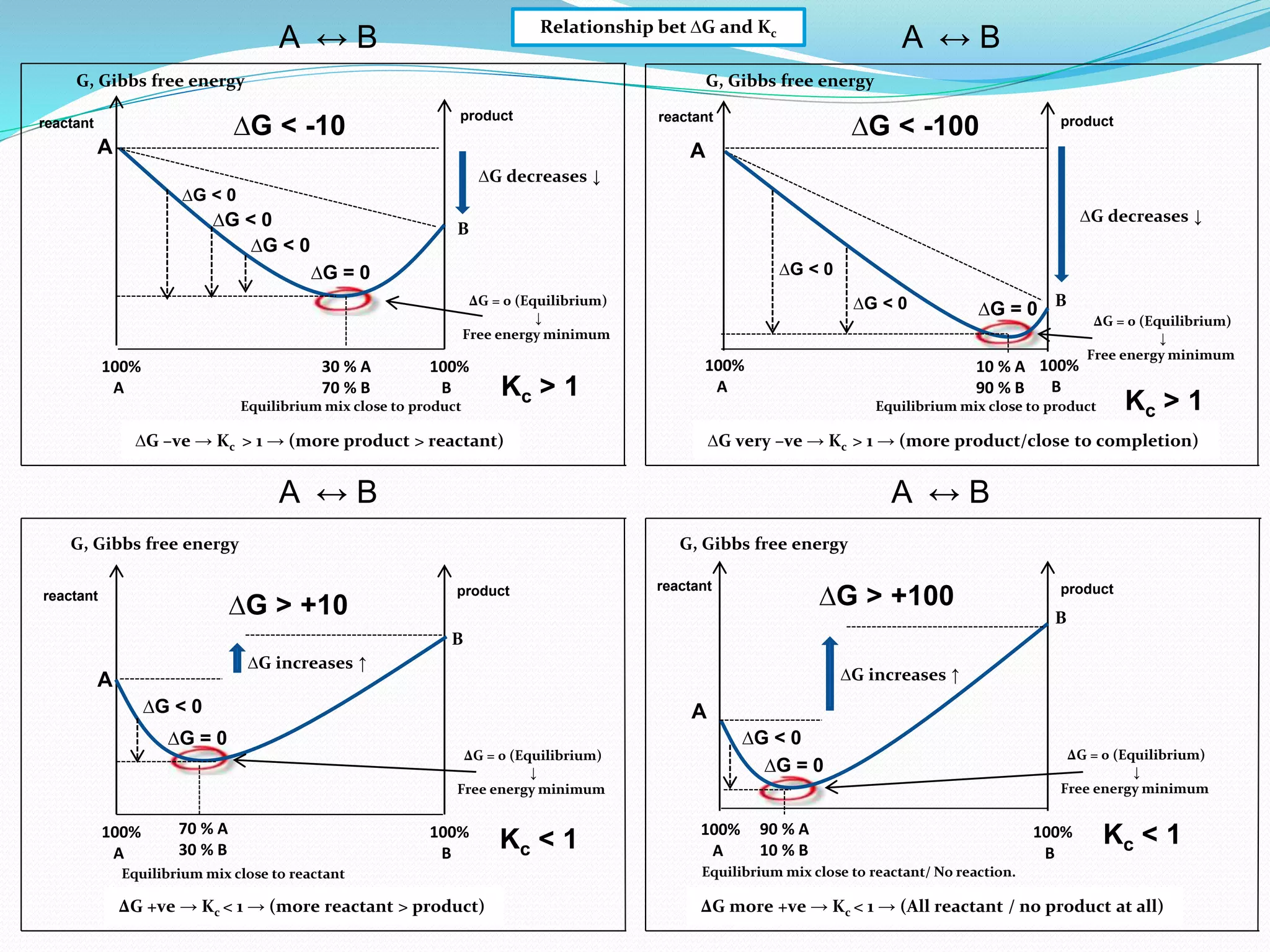
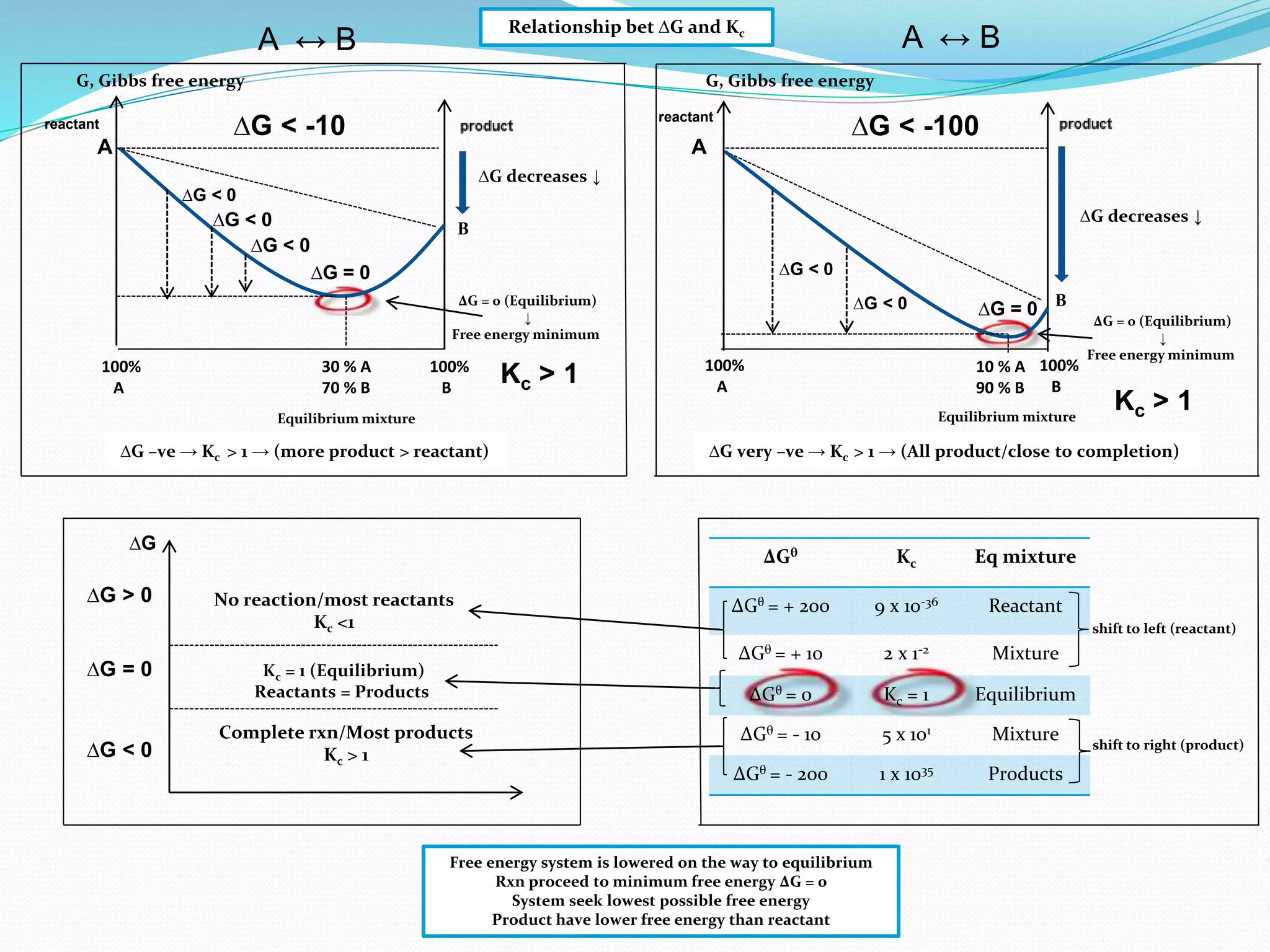
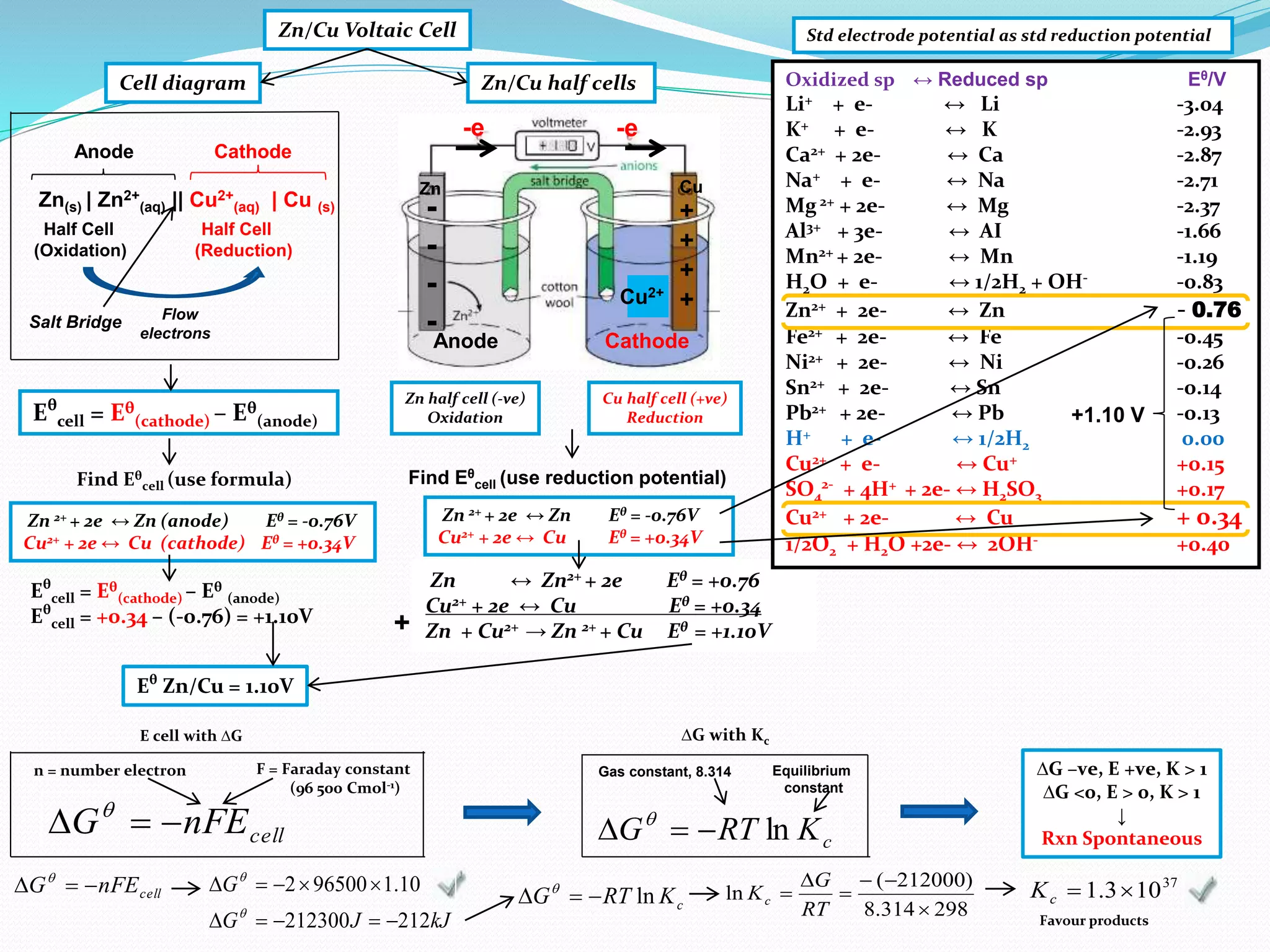
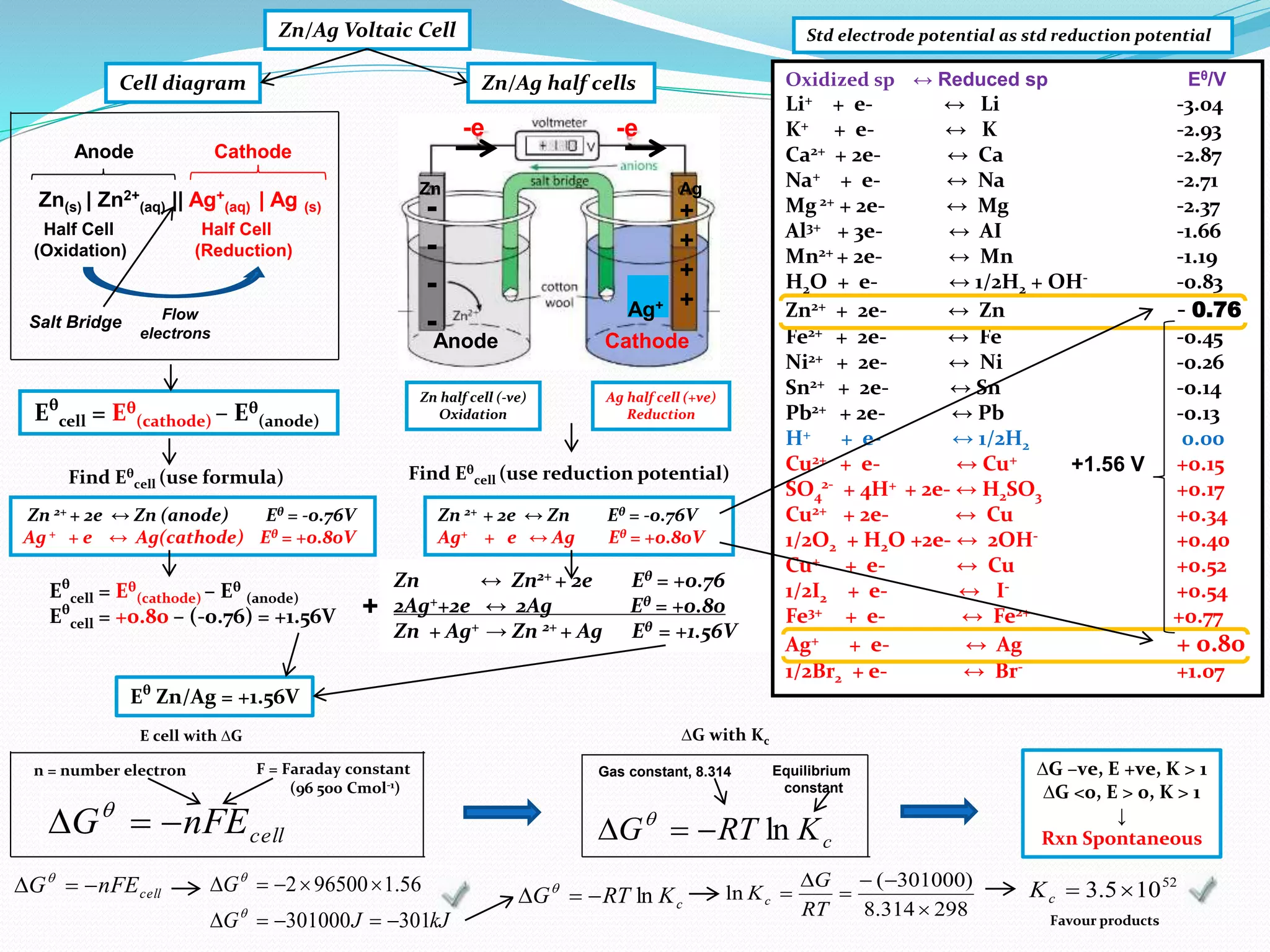
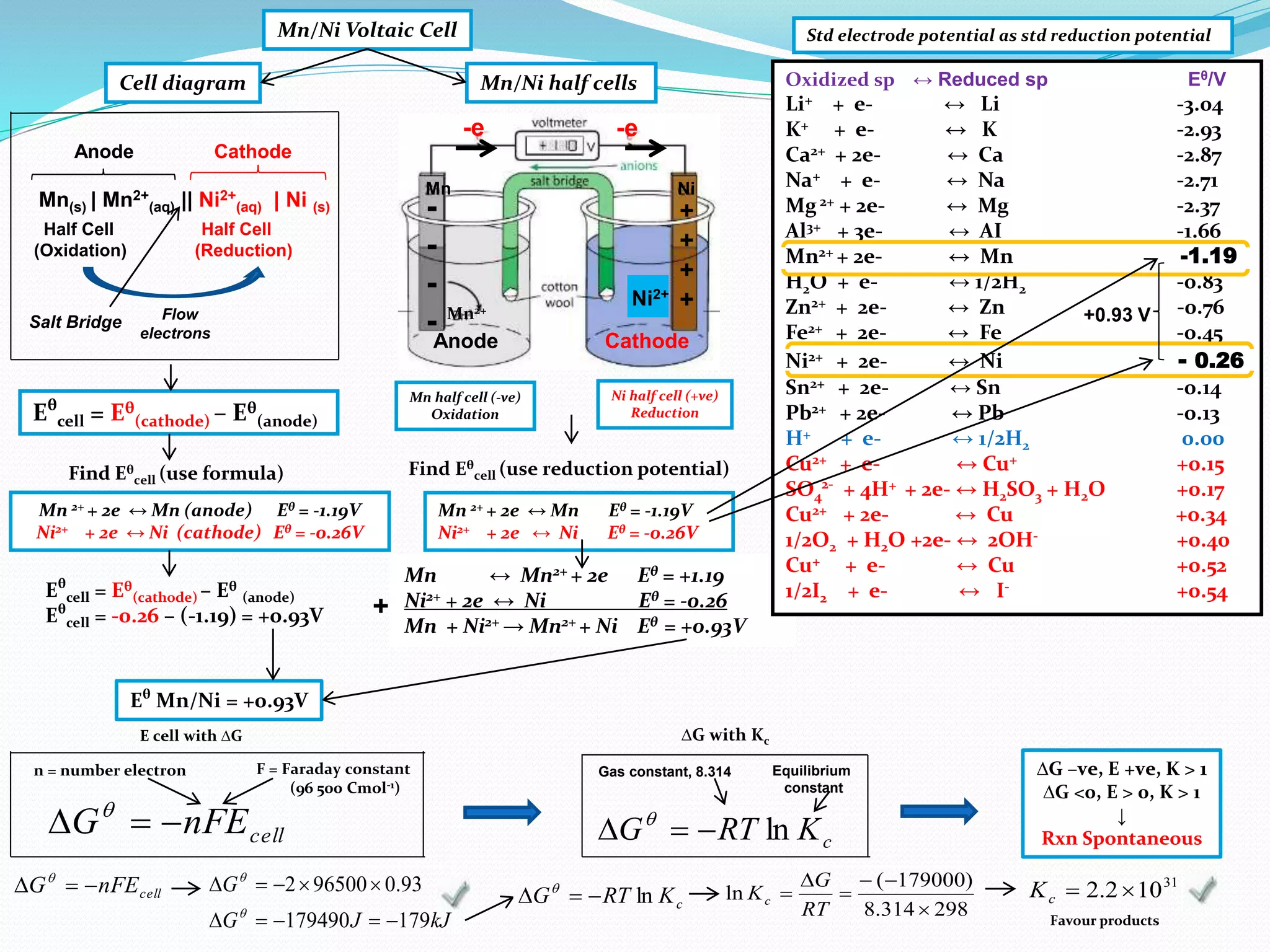
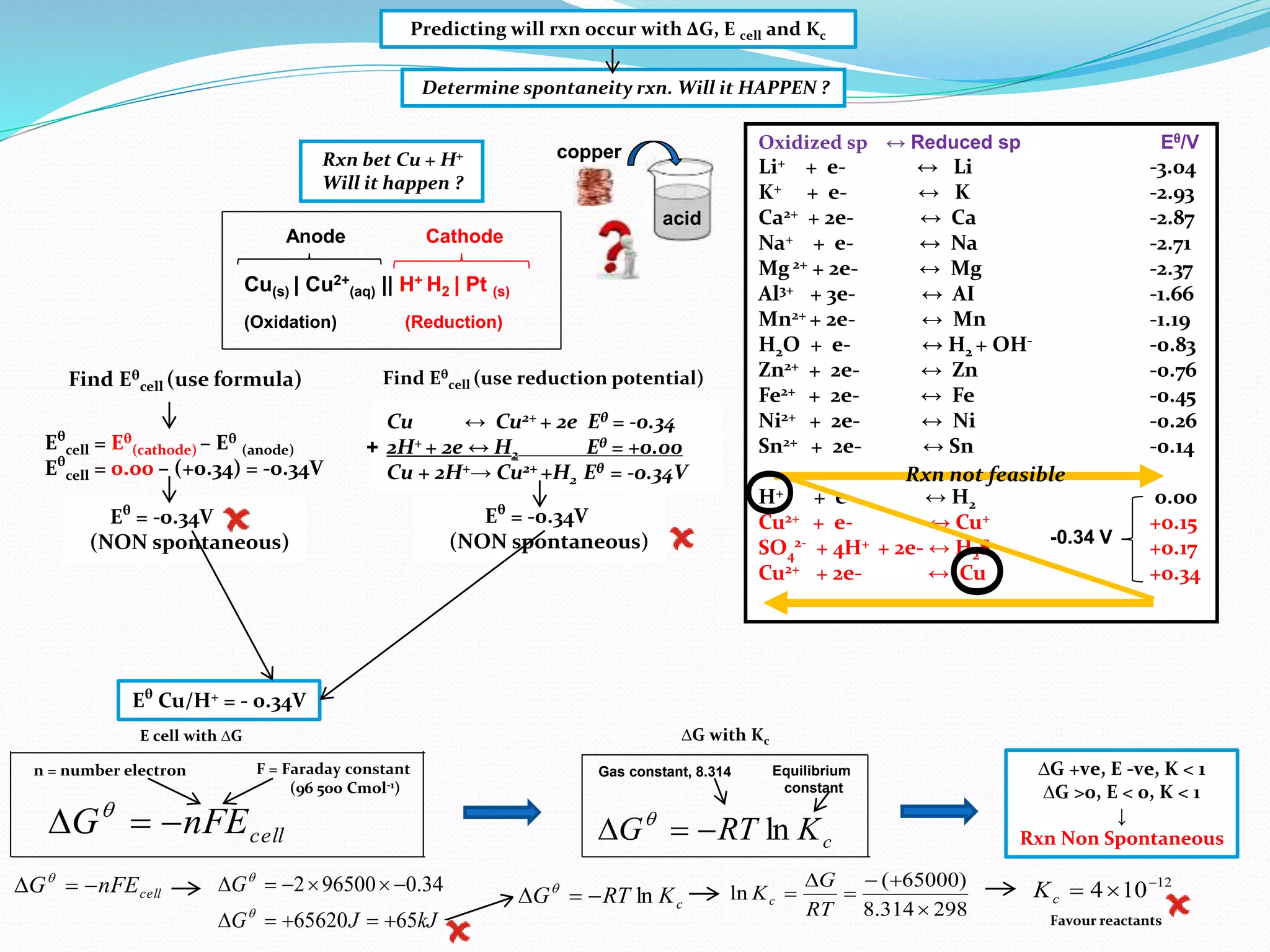
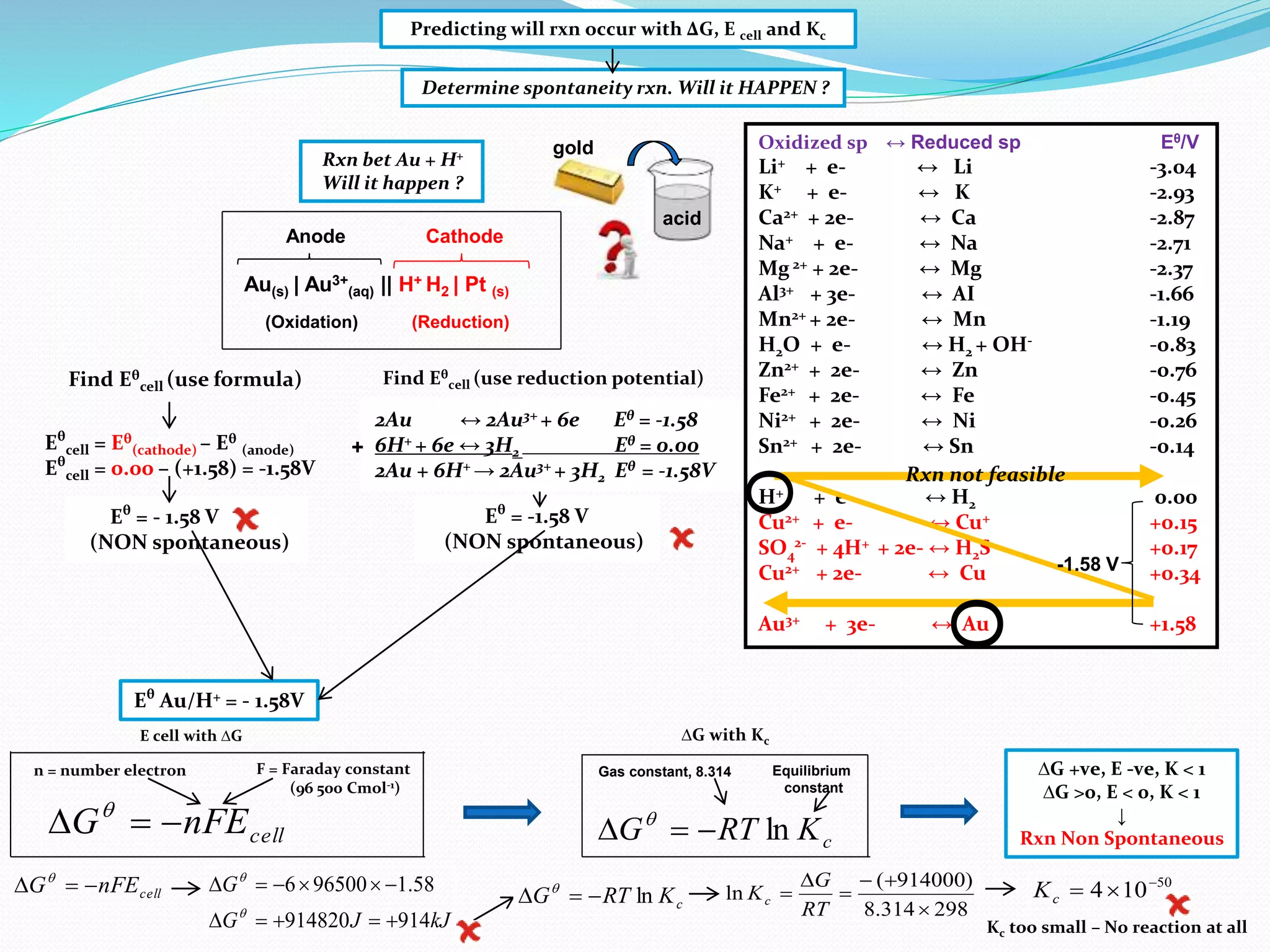
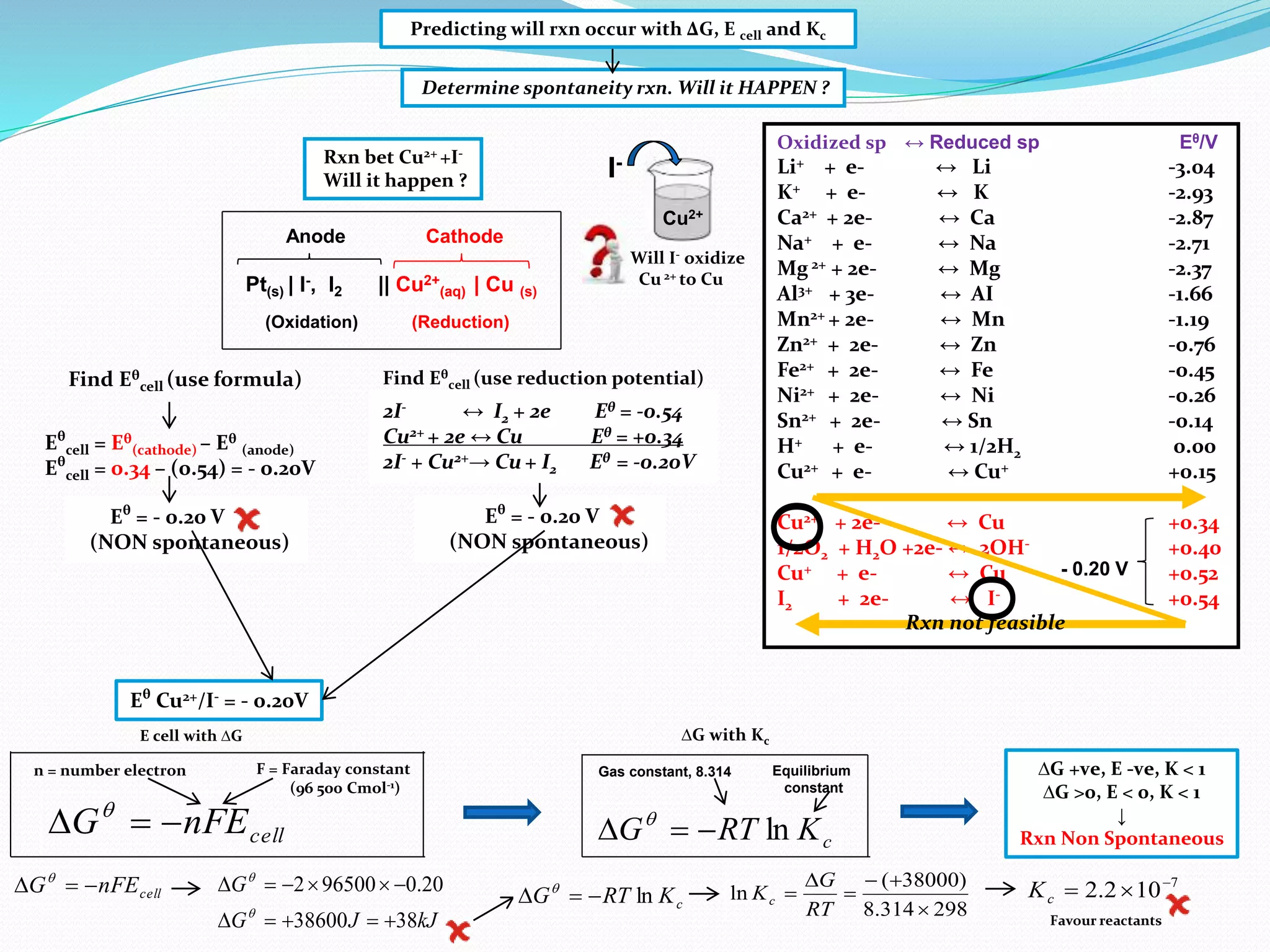
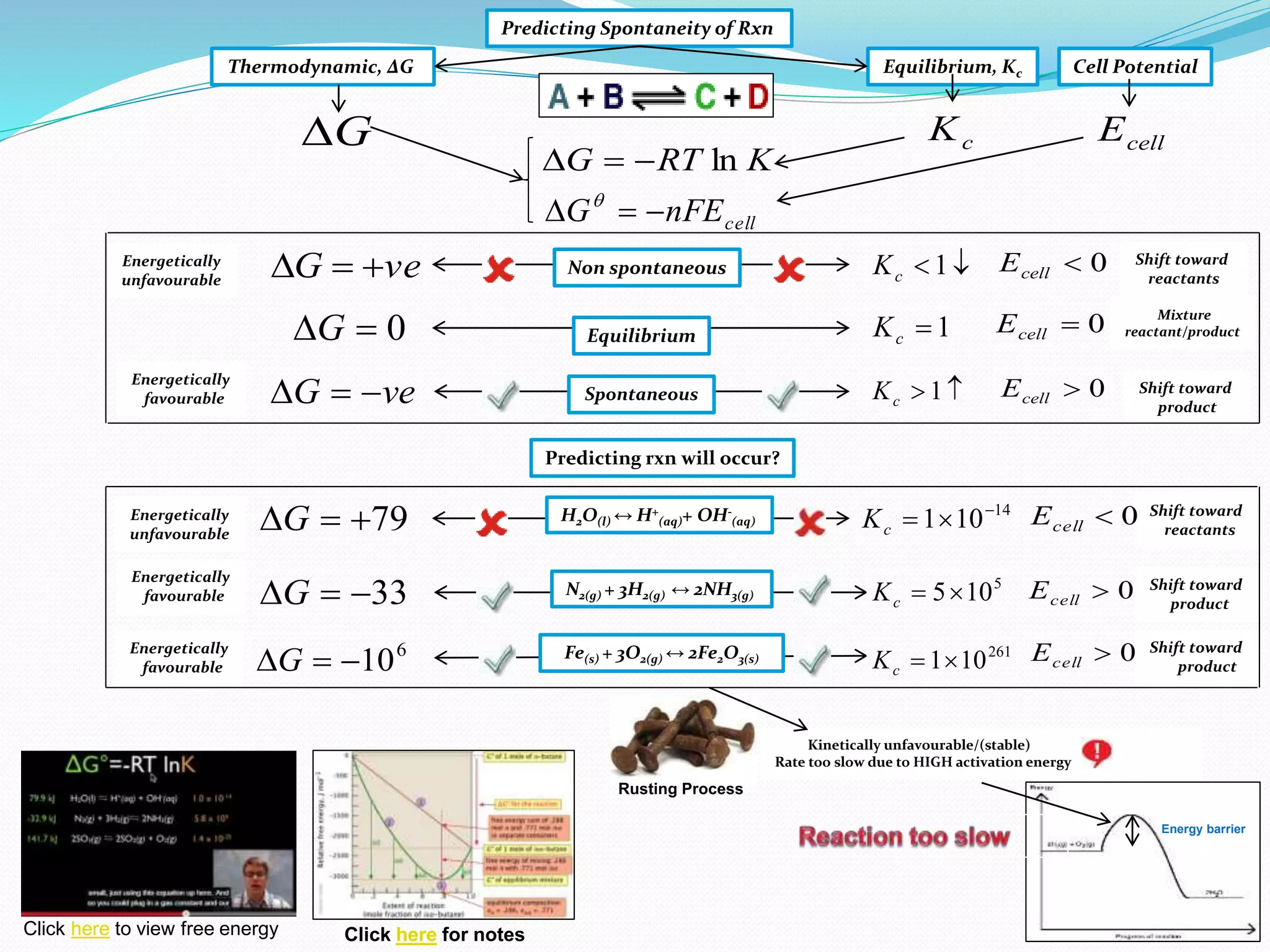
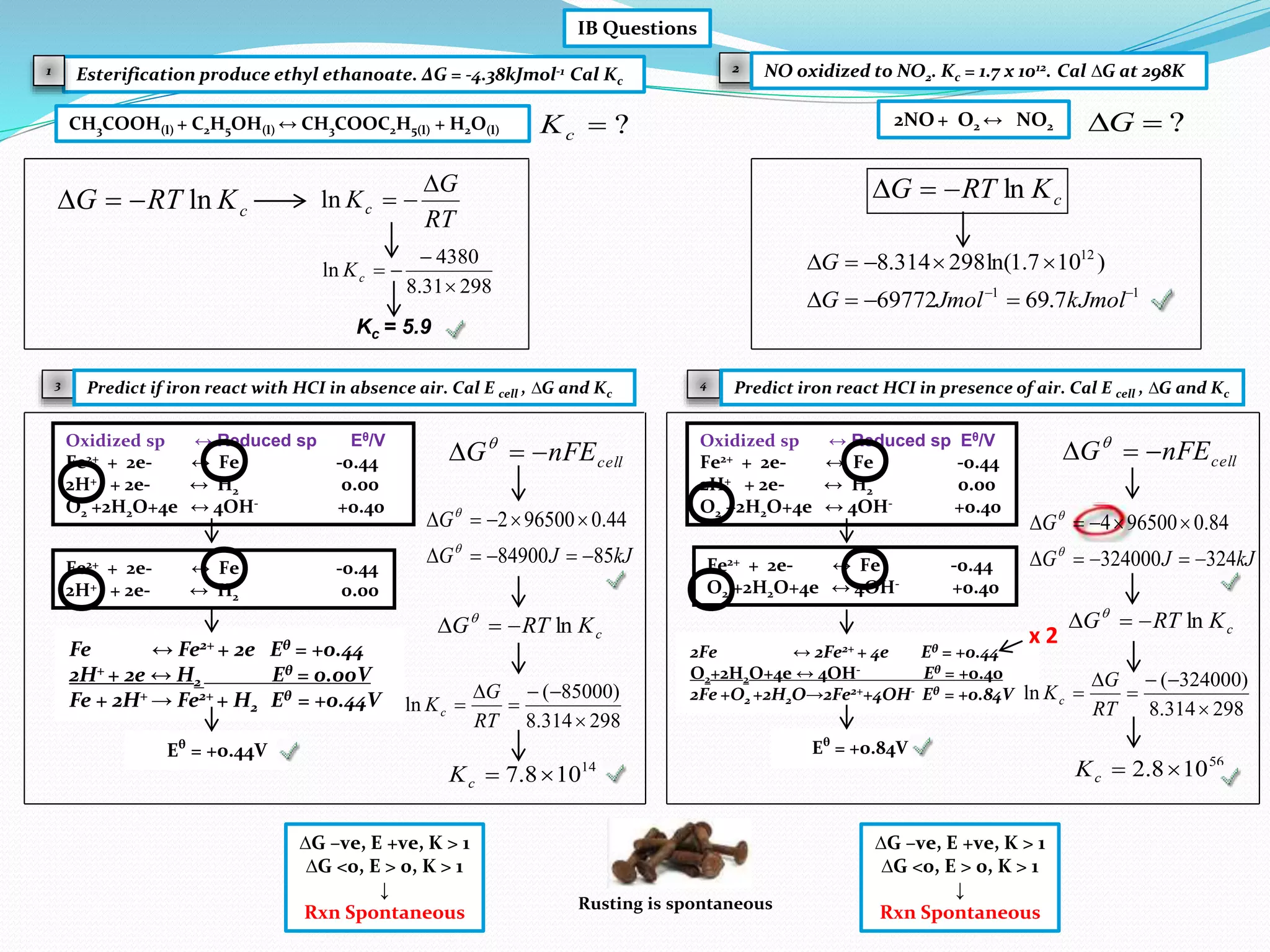
This document provides a tutorial on Gibbs free energy change, equilibrium, and cell potential in electrochemistry. It discusses the relationships between Gibbs free energy change (ΔG), entropy change (ΔS), enthalpy change (ΔH), equilibrium constant (Kc), and cell potential (Ecell). Graphs and equations are presented to show how ΔG relates to the position and extent of chemical equilibrium. The standard reduction potentials of various half-cell reactions are also listed.

1. http://lawrencekok.blogspot.com
Prepared by
Lawrence Kok
Tutorial on Gibbs Free Energy Change, Equilibrium and Cell Potential

2. cellnFEG  
Relationship between
Energetics and Equilibrium
cKRTG ln 
STHG 
Enthalpy
change
Entropy
change
Equilibrium
constant
Gibbs free
energy change
H
G
Relationship bet ∆G, Kc and E cell
cellnFEG  
STHG  cKRTG ln 
cK
Relationship between
Energetics and Cell Potential

G cellE
Gibbs free
energy change
Cell potential
F = Faraday constant
(96 500 Cmol-1)
n = number
electron
Relationship bet ∆G, Kc and Ecell
ΔGθ Kc Eθ/V Extent of rxn
> 0 < 1 < 0 No Reaction
Non spontaneous
ΔGθ = 0 Kc = 1 0 Equilibrium
Mix reactant/product
< 0 > 1 > 0 Reaction complete
Spontaneous
ΔGθ Kc Eq mixture
ΔGθ = + 200 9 x 10-36 Reactants
ΔGθ = + 10 2 x 1-2 Mixture
ΔGθ = 0 Kc = 1 Equilibrium
ΔGθ = - 10 5 x 101 Mixture
ΔGθ = - 200 1 x 1035 Products
Relationship bet ∆G and Kc
shift to left (reactant)
shift to right (products)
cellE

G
cK
K
nF
RT
E cell ln

3. Magnitude of Kc Extend of reaction
How far rxn shift to right or left?
Not how fast
cK
Position of equilibrium
cK
Temp
dependent
Extend
of rxn
Not how fast
Shift to left/
favour reactant
Shift to right/
favour product
cK
Relationship between
Equilibrium and Energetics
cKRTG ln 
STHG 
Enthalpy
change
Entropy
change
Equilibrium
constant
Gibbs free energy change
H
G cK
G
Energetically
Thermodynamically
Favourable/feasible
ΔGθ ln K Kc Eq mixture
ΔGθ -ve
< 0
Positive
( + )
Kc > 1 Product
(Right)
ΔGθ +ve
> 0
Negative
( - )
Kc < 1 Reactant
(left)
ΔGθ = 0 0 Kc = 1 Equilibrium
Measure work
available from system
Sign predict
spontaneity of rxn
Negative (-ve)
spontaneous
Positive (+ve)
NOT
spontaneous
veG  veG 
NOT
favourable
Energetically
favourable
Product formation NO product
cKRTG ln 

4. Magnitude of Kc Extend of reaction
How far rxn shift to right or left?
Not how fast
cK
Position of equilibrium
cK
Temp
dependent
Extend
of rxn
Not how fast
Shift to left/
favour reactant
Shift to right/
favour product
cK
Relationship between
Equilibrium and Energetics
cKRTG ln 
STHG 
Enthalpy
change
Entropy
change
Equilibrium
constant
Gibbs free energy change
H
G cK
ΔGθ ln K Kc Eq mixture
ΔGθ -ve
< 0
Positive
( + )
Kc > 1 Product
(Right)
ΔGθ +ve
> 0
Negative
( - )
Kc < 1 Reactant
(left)
ΔGθ = 0 0 Kc = 1 Equilibrium
cKRTG ln 
STHG 
∆Hsys ∆Ssys ∆Gsys Description
- +
∆G = ∆H - T∆S
∆G = - ve
Spontaneous, All Temp
+ -
∆G = ∆H - T∆S
∆G = + ve
Non spontaneous, All Temp
+ +
∆G = ∆H - T∆S
∆G = - ve
Spontaneous, High ↑ Temp
- -
∆G = ∆H - T∆S
∆G = - ve
Spontaneous, Low ↓ Temp
Relationship bet ∆G and Kc

5. G
Energetically
Thermodynamically
Favourable/feasible
Sign predict
spontaneity of rxn
veG  veG 
NOT
favourable
Energetically
favourable
Product formation NO product
KRTG ln
Predict will rxn occur with ΔG and Kc
cK
Very SMALL
Kc < 1
Shift to right/
favour product
Shift to left/
favour reactant
Very BIG
Kc > 1
veG veG 
KRTG ln
1cK 1cK
Negative (-ve)
spontaneous
Positive (+ve)
NOT
spontaneous
Relationship bet ∆G and Kc
ΔGθ Kc Eq mixture
ΔGθ = + 200 9 x 10-36 Reactant
ΔGθ = + 10 2 x 1-2 Mixture
ΔGθ = 0 Kc = 1 Equilibrium
ΔGθ = - 10 5 x 101 Mixture
ΔGθ = - 200 1 x 1035 Products
shift to left (reactant)
shift to right (product)
G, Gibbs free energy
A
Mixture composition
B
100% A 100% B
∆G decreases ↓
30 % A
70 % B
Equilibrium mixture
∆G < 0
∆G = 0 (Equilibrium)
↓
Free energy minimum
∆G < 0
∆G < 0
∆G = 0
Free energy system is lowered on the way to equilibrium
Rxn proceed to minimum free energy ∆G = 0
System seek lowest possible free energy
Product have lower free energy than reactant
∆G < 0 product
reactant

6. G
Energetically
Thermodynamically
Favourable/feasible
Sign predict
spontaneity of rxn
veG  veG 
NOT
favourable
Energetically
favourable
Product formation NO product
KRTG ln
cK
Very SMALL
Kc < 1
Shift to right/
favour product
Shift to left/
favour reactant
Very BIG
Kc > 1
veG veG 
KRTG ln
1cK 1cK
Negative (-ve)
spontaneous
Positive (+ve)
NOT
spontaneous
Relationship bet ∆G, Q and Kc
G, Gibbs free energy
A
B
100% A 100% B
∆G decreases ↓
30 % A
70 % B
Equilibrium mixture
∆G < 0
∆G = 0 (Equilibrium)
↓
Free energy
minimum
∆G < 0
∆G < 0
∆G = 0
∆G < 0 product
reactant
G, Gibbs free energy
reactant product∆G < 0
A
B
∆G decreases ↓
100% A 100% B30 % A
70 % B
∆G = 0
Q = K
∆G < 0
Q < K
∆G > 0
∆G < 0
Q > K
∆G > 0
A ↔ B A ↔ B
Equilibrium mixture
Predict will rxn occur with ΔG and Kc

7. Relationship bet ∆G and Kc
G, Gibbs free energy
A
B
100%
A
100%
B
∆G decreases ↓
30 % A
70 % B
Equilibrium mix close to product
∆G < 0
∆G = 0 (Equilibrium)
↓
Free energy minimum
∆G < 0
∆G < 0
∆G = 0
∆G < -10
Kc > 1
A ↔ B A ↔ B
G, Gibbs free energy
A
B
∆G decreases ↓
∆G < -100
100%
A
100%
B
∆G = 0 (Equilibrium)
↓
Free energy minimum
Kc > 1Equilibrium mix close to product
10 % A
90 % B
∆G < 0
∆G < 0 ∆G = 0
∆G very –ve → Kc > 1 → (more product/close to completion)∆G –ve → Kc > 1 → (more product > reactant)
A ↔ B
G, Gibbs free energy
100%
A
100%
B
A
B
∆G +ve → Kc < 1 → (more reactant > product)
∆G > +10
∆G = 0 (Equilibrium)
↓
Free energy minimum
Kc < 1
∆G increases ↑
70 % A
30 % B
Equilibrium mix close to reactant
∆G < 0
∆G = 0
A ↔ B
G, Gibbs free energy
∆G more +ve → Kc < 1 → (All reactant / no product at all)
A
∆G = 0 (Equilibrium)
↓
Free energy minimum
Kc < 1100%
A
100%
B
Equilibrium mix close to reactant/ No reaction.
∆G > +100
B
90 % A
10 % B
∆G increases ↑
∆G = 0
∆G < 0
reactant
reactant
reactant
reactant
productproduct
product product

8. Relationship bet ∆G and Kc
shift to left (reactant)
shift to right (product)
G, Gibbs free energy
A
B
100%
A
100%
B
∆G decreases ↓
30 % A
70 % B
Equilibrium mixture
∆G < 0
∆G = 0 (Equilibrium)
↓
Free energy minimum
∆G < 0
∆G < 0
∆G = 0
Free energy system is lowered on the way to equilibrium
Rxn proceed to minimum free energy ∆G = 0
System seek lowest possible free energy
Product have lower free energy than reactant
∆G < -10
Kc > 1
A ↔ B A ↔ B
G, Gibbs free energy
A
B
∆G decreases ↓
∆G < -100
100%
A
100%
B
∆G = 0 (Equilibrium)
↓
Free energy minimum
Kc > 1Equilibrium mixture
10 % A
90 % B
∆G < 0
∆G < 0 ∆G = 0
∆G very –ve → Kc > 1 → (All product/close to completion)∆G –ve → Kc > 1 → (more product > reactant)
∆G
∆G = 0
∆G > 0
∆G < 0
No reaction/most reactants
Kc <1
Complete rxn/Most products
Kc > 1
Kc = 1 (Equilibrium)
Reactants = Products
reactant
reactant
ΔGθ Kc Eq mixture
ΔGθ = + 200 9 x 10-36 Reactant
ΔGθ = + 10 2 x 1-2 Mixture
ΔGθ = 0 Kc = 1 Equilibrium
ΔGθ = - 10 5 x 101 Mixture
ΔGθ = - 200 1 x 1035 Products

9. 298314.8
)212000(
ln





RT
G
Kc
Zn ↔ Zn2+ + 2e Eθ = +0.76
Cu2+ + 2e ↔ Cu Eθ = +0.34
Zn + Cu2+ → Zn 2+ + Cu Eθ = +1.10V
Zn half cell (-ve)
Oxidation
Cu half cell (+ve)
Reduction
Anode Cathode
Zn(s) | Zn2+
(aq) || Cu2+
(aq) | Cu (s)
Cell diagram
Anode Cathode
Half Cell Half Cell
(Oxidation) (Reduction)
Salt Bridge Flow
electrons
Zn/Cu Voltaic Cell
-e -e
Zn/Cu half cells
Eθ
cell = Eθ
(cathode) – Eθ
(anode)
Eθ
cell = +0.34 – (-0.76) = +1.10V
Zn 2+ + 2e ↔ Zn (anode) Eθ = -0.76V
Cu2+ + 2e ↔ Cu (cathode) Eθ = +0.34V
Std electrode potential as std reduction potential
Find Eθ
cell (use reduction potential)Find Eθ
cell (use formula)
Eθ
cell = Eθ
(cathode) – Eθ
(anode)
Zn 2+ + 2e ↔ Zn Eθ = -0.76V
Cu2+ + 2e ↔ Cu Eθ = +0.34V
Oxidized sp ↔ Reduced sp Eθ/V
Li+ + e- ↔ Li -3.04
K+ + e- ↔ K -2.93
Ca2+ + 2e- ↔ Ca -2.87
Na+ + e- ↔ Na -2.71
Mg 2+ + 2e- ↔ Mg -2.37
Al3+ + 3e- ↔ AI -1.66
Mn2+ + 2e- ↔ Mn -1.19
H2O + e- ↔ 1/2H2 + OH- -0.83
Zn2+ + 2e- ↔ Zn - 0.76
Fe2+ + 2e- ↔ Fe -0.45
Ni2+ + 2e- ↔ Ni -0.26
Sn2+ + 2e- ↔ Sn -0.14
Pb2+ + 2e- ↔ Pb -0.13
H+ + e- ↔ 1/2H2 0.00
Cu2+ + e- ↔ Cu+ +0.15
SO4
2-
+ 4H+ + 2e- ↔ H2SO3 +0.17
Cu2+ + 2e- ↔ Cu + 0.34
1/2O2 + H2O +2e- ↔ 2OH- +0.40
+
+1.10 V
Eθ
Zn/Cu = 1.10V
Cu2+
-
-
-
-
Zn Cu
+
+
+
+
cellnFEG  
E cell with ∆G
F = Faraday constant
(96 500 Cmol-1)
n = number electron
cellnFEG  
kJJG
G
212212300
10.1965002




∆G –ve, E +ve, K > 1
∆G <0, E > 0, K > 1
↓
Rxn SpontaneouscKRTG ln 
Equilibrium
constant
Gas constant, 8.314
∆G with Kc
cKRTG ln  37
103.1 cK
Favour products

10. Zn ↔ Zn2+ + 2e Eθ = +0.76
2Ag++2e ↔ 2Ag Eθ = +0.80
Zn + Ag+ → Zn 2+ + Ag Eθ = +1.56V
Zn half cell (-ve)
Oxidation
Ag half cell (+ve)
Reduction
Anode Cathode
Zn(s) | Zn2+
(aq) || Ag+
(aq) | Ag (s)
Cell diagram
Anode Cathode
Half Cell Half Cell
(Oxidation) (Reduction)
Salt Bridge Flow
electrons
Zn/Ag Voltaic Cell
-e -e
Zn/Ag half cells
Eθ
cell = Eθ
(cathode) – Eθ
(anode)
Eθ
cell = +0.80 – (-0.76) = +1.56V
Zn 2+ + 2e ↔ Zn (anode) Eθ = -0.76V
Ag+ + e ↔ Ag(cathode) Eθ = +0.80V
Std electrode potential as std reduction potential
Find Eθ
cell (use reduction potential)Find Eθ
cell (use formula)
Eθ
cell = Eθ
(cathode) – Eθ
(anode)
Zn 2+ + 2e ↔ Zn Eθ = -0.76V
Ag+ + e ↔ Ag Eθ = +0.80V
Oxidized sp ↔ Reduced sp Eθ/V
Li+ + e- ↔ Li -3.04
K+ + e- ↔ K -2.93
Ca2+ + 2e- ↔ Ca -2.87
Na+ + e- ↔ Na -2.71
Mg 2+ + 2e- ↔ Mg -2.37
Al3+ + 3e- ↔ AI -1.66
Mn2+ + 2e- ↔ Mn -1.19
H2O + e- ↔ 1/2H2 + OH- -0.83
Zn2+ + 2e- ↔ Zn - 0.76
Fe2+ + 2e- ↔ Fe -0.45
Ni2+ + 2e- ↔ Ni -0.26
Sn2+ + 2e- ↔ Sn -0.14
Pb2+ + 2e- ↔ Pb -0.13
H+ + e- ↔ 1/2H2 0.00
Cu2+ + e- ↔ Cu+ +0.15
SO4
2-
+ 4H+ + 2e- ↔ H2SO3 +0.17
Cu2+ + 2e- ↔ Cu +0.34
1/2O2 + H2O +2e- ↔ 2OH- +0.40
Cu+ + e- ↔ Cu +0.52
1/2I2 + e- ↔ I- +0.54
Fe3+ + e- ↔ Fe2+ +0.77
Ag+ + e- ↔ Ag + 0.80
1/2Br2 + e- ↔ Br- +1.07
+
+1.56 V
Ag
Eθ
Zn/Ag = +1.56V
Ag+
-
-
-
-
+
+
+
+
Zn
E cell with ∆G
cellnFEG  
n = number electron F = Faraday constant
(96 500 Cmol-1)
cellnFEG  
kJJG
G
301301000
56.1965002




∆G with Kc
cKRTG ln 
Gas constant, 8.314 Equilibrium
constant
cKRTG ln 
298314.8
)301000(
ln





RT
G
Kc
52
105.3 cK
∆G –ve, E +ve, K > 1
∆G <0, E > 0, K > 1
↓
Rxn Spontaneous
Favour products

11. Mn ↔ Mn2+ + 2e Eθ = +1.19
Ni2+ + 2e ↔ Ni Eθ = -0.26
Mn + Ni2+ → Mn2+ + Ni Eθ = +0.93V
Mn half cell (-ve)
Oxidation
Ni half cell (+ve)
Reduction
Anode Cathode
Mn(s) | Mn2+
(aq) || Ni2+
(aq) | Ni (s)
Cell diagram
Anode Cathode
Half Cell Half Cell
(Oxidation) (Reduction)
Salt Bridge Flow
electrons
Mn/Ni Voltaic Cell
-e -e
Mn/Ni half cells
Eθ
cell = Eθ
(cathode) – Eθ
(anode)
Eθ
cell = -0.26 – (-1.19) = +0.93V
Mn 2+ + 2e ↔ Mn (anode) Eθ = -1.19V
Ni2+ + 2e ↔ Ni (cathode) Eθ = -0.26V
Std electrode potential as std reduction potential
Find Eθ
cell (use reduction potential)Find Eθ
cell (use formula)
Eθ
cell = Eθ
(cathode) – Eθ
(anode)
Mn 2+ + 2e ↔ Mn Eθ = -1.19V
Ni2+ + 2e ↔ Ni Eθ = -0.26V
Oxidized sp ↔ Reduced sp Eθ/V
Li+ + e- ↔ Li -3.04
K+ + e- ↔ K -2.93
Ca2+ + 2e- ↔ Ca -2.87
Na+ + e- ↔ Na -2.71
Mg 2+ + 2e- ↔ Mg -2.37
Al3+ + 3e- ↔ AI -1.66
Mn2+ + 2e- ↔ Mn -1.19
H2O + e- ↔ 1/2H2 -0.83
Zn2+ + 2e- ↔ Zn -0.76
Fe2+ + 2e- ↔ Fe -0.45
Ni2+ + 2e- ↔ Ni - 0.26
Sn2+ + 2e- ↔ Sn -0.14
Pb2+ + 2e- ↔ Pb -0.13
H+ + e- ↔ 1/2H2 0.00
Cu2+ + e- ↔ Cu+ +0.15
SO4
2-
+ 4H+ + 2e- ↔ H2SO3 + H2O +0.17
Cu2+ + 2e- ↔ Cu +0.34
1/2O2 + H2O +2e- ↔ 2OH- +0.40
Cu+ + e- ↔ Cu +0.52
1/2I2 + e- ↔ I- +0.54
+
+0.93 V
Eθ
Mn/Ni = +0.93V
Ni2+
-
-
-
-
NiMn
+
+
+
+Mn2+
E cell with ∆G
cellnFEG  
n = number electron F = Faraday constant
(96 500 Cmol-1)
cellnFEG  
kJJG
G
179179490
93.0965002




cKRTG ln 
298314.8
)179000(
ln





RT
G
Kc
cKRTG ln 
∆G with Kc
Gas constant, 8.314 Equilibrium
constant
∆G –ve, E +ve, K > 1
∆G <0, E > 0, K > 1
↓
Rxn Spontaneous
31
102.2 cK
Favour products

12. Oxidized sp ↔ Reduced sp Eθ/V
Li+ + e- ↔ Li -3.04
K+ + e- ↔ K -2.93
Ca2+ + 2e- ↔ Ca -2.87
Na+ + e- ↔ Na -2.71
Mg 2+ + 2e- ↔ Mg -2.37
Al3+ + 3e- ↔ AI -1.66
Mn2+ + 2e- ↔ Mn -1.19
H2O + e- ↔ H2 + OH- -0.83
Zn2+ + 2e- ↔ Zn -0.76
Fe2+ + 2e- ↔ Fe -0.45
Ni2+ + 2e- ↔ Ni -0.26
Sn2+ + 2e- ↔ Sn -0.14
H+ + e- ↔ H2 0.00
Cu2+ + e- ↔ Cu+ +0.15
SO4
2-
+ 4H+ + 2e- ↔ H2S +0.17
Cu2+ + 2e- ↔ Cu +0.34
Cu ↔ Cu2+ + 2e Eθ = -0.34
2H+ + 2e ↔ H2 Eθ = +0.00
Cu + 2H+→ Cu2+ +H2 Eθ = -0.34V
Rxn bet Cu + H+
Will it happen ?
Eθ
= -0.34V
(NON spontaneous)
О
Cu(s) | Cu2+
(aq) || H+ H2 | Pt (s)
(Oxidation) (Reduction)
Anode Cathode
Find Eθ
cell (use formula)
Eθ
cell = Eθ
(cathode) – Eθ
(anode)
Eθ
cell = 0.00 – (+0.34) = -0.34V
Eθ
= -0.34V
(NON spontaneous)
О
Rxn not feasible
Determine spontaneity rxn. Will it HAPPEN ?
Find Eθ
cell (use reduction potential)
Eθ
Cu/H+ = - 0.34V
E cell with ∆G
cellnFEG  
n = number electron F = Faraday constant
(96 500 Cmol-1)
cellnFEG  
kJJG
G
6565620
34.0965002




cKRTG ln 
Gas constant, 8.314 Equilibrium
constant
∆G with Kc
cKRTG ln 
298314.8
)65000(
ln





RT
G
Kc
∆G +ve, E -ve, K < 1
∆G >0, E < 0, K < 1
↓
Rxn Non Spontaneous
12
104 
cK
Favour reactants
-0.34 V
acid
copper
Predicting will rxn occur with ΔG, E cell and Kc
+

13. Oxidized sp ↔ Reduced sp Eθ/V
Li+ + e- ↔ Li -3.04
K+ + e- ↔ K -2.93
Ca2+ + 2e- ↔ Ca -2.87
Na+ + e- ↔ Na -2.71
Mg 2+ + 2e- ↔ Mg -2.37
Al3+ + 3e- ↔ AI -1.66
Mn2+ + 2e- ↔ Mn -1.19
H2O + e- ↔ H2 + OH- -0.83
Zn2+ + 2e- ↔ Zn -0.76
Fe2+ + 2e- ↔ Fe -0.45
Ni2+ + 2e- ↔ Ni -0.26
Sn2+ + 2e- ↔ Sn -0.14
H+ + e- ↔ H2 0.00
Cu2+ + e- ↔ Cu+ +0.15
SO4
2-
+ 4H+ + 2e- ↔ H2S +0.17
Cu2+ + 2e- ↔ Cu +0.34
Au3+ + 3e- ↔ Au +1.58
Rxn bet Au + H+
Will it happen ?
Eθ
= -1.58 V
(NON spontaneous)
О
Au(s) | Au3+
(aq) || H+ H2 | Pt (s)
(Oxidation) (Reduction)
Anode Cathode
Find Eθ
cell (use formula)
Eθ
cell = Eθ
(cathode) – Eθ
(anode)
Eθ
cell = 0.00 – (+1.58) = -1.58V
Eθ
= - 1.58 V
(NON spontaneous)
О
Rxn not feasible
Determine spontaneity rxn. Will it HAPPEN ?
Find Eθ
cell (use reduction potential)
Eθ
Au/H+ = - 1.58V
E cell with ∆G
cellnFEG  
n = number electron F = Faraday constant
(96 500 Cmol-1)
cellnFEG  
kJJG
G
914914820
58.1965006




cKRTG ln 
Gas constant, 8.314 Equilibrium
constant
∆G with Kc
cKRTG ln 
298314.8
)914000(
ln





RT
G
Kc
∆G +ve, E -ve, K < 1
∆G >0, E < 0, K < 1
↓
Rxn Non Spontaneous
50
104 
cK
Kc too small – No reaction at all
-1.58 V
acid
gold
2Au ↔ 2Au3+ + 6e Eθ = -1.58
6H+ + 6e ↔ 3H2 Eθ = 0.00
2Au + 6H+ → 2Au3+ + 3H2 Eθ = -1.58V
Predicting will rxn occur with ΔG, E cell and Kc
+

14. Eθ
= - 0.20 V
(NON spontaneous)
(Oxidation) (Reduction)
Anode Cathode
Find Eθ
cell (use formula)
Eθ
cell = Eθ
(cathode) – Eθ
(anode)
Eθ
cell = 0.34 – (0.54) = - 0.20V
Eθ
= - 0.20 V
(NON spontaneous)
Determine spontaneity rxn. Will it HAPPEN ?
Find Eθ
cell (use reduction potential)
Eθ
Cu2+/I- = - 0.20V
E cell with ∆G
cellnFEG  
n = number electron F = Faraday constant
(96 500 Cmol-1)
cellnFEG  
kJJG
G
3838600
20.0965002




cKRTG ln 
Gas constant, 8.314 Equilibrium
constant
∆G with Kc
cKRTG ln 
298314.8
)38000(
ln





RT
G
Kc
∆G +ve, E -ve, K < 1
∆G >0, E < 0, K < 1
↓
Rxn Non Spontaneous
7
102.2 
cK
-1.58 V
Cu2+
I-Rxn bet Cu2+ +I-
Will it happen ?
2I- ↔ I2 + 2e Eθ = -0.54
Cu2+ + 2e ↔ Cu Eθ = +0.34
2I- + Cu2+→ Cu + I2 Eθ = -0.20V
Pt(s) | I-, I2 || Cu2+
(aq) | Cu (s)
Favour reactants
Oxidized sp ↔ Reduced sp Eθ/V
Li+ + e- ↔ Li -3.04
K+ + e- ↔ K -2.93
Ca2+ + 2e- ↔ Ca -2.87
Na+ + e- ↔ Na -2.71
Mg 2+ + 2e- ↔ Mg -2.37
Al3+ + 3e- ↔ AI -1.66
Mn2+ + 2e- ↔ Mn -1.19
Zn2+ + 2e- ↔ Zn -0.76
Fe2+ + 2e- ↔ Fe -0.45
Ni2+ + 2e- ↔ Ni -0.26
Sn2+ + 2e- ↔ Sn -0.14
H+ + e- ↔ 1/2H2 0.00
Cu2+ + e- ↔ Cu+ +0.15
Cu2+ + 2e- ↔ Cu +0.34
1/2O2 + H2O +2e- ↔ 2OH- +0.40
Cu+ + e- ↔ Cu +0.52
I2 + 2e- ↔ I- +0.54
Rxn not feasible
О
О
- 0.20 V
Predicting will rxn occur with ΔG, E cell and Kc
Will I- oxidize
Cu 2+ to Cu

15. Click here to view free energy
Predicting Spontaneity of Rxn
Thermodynamic, ΔG Equilibrium, Kc
 1cK
 1cK
KRTG ln
G
veG 
cK
1cK
Energetically
favourable
0G
Predicting rxn will occur?
N2(g) + 3H2(g) ↔ 2NH3(g)
H2O(l) ↔ H+
(aq)+ OH-
(aq)
Shift toward
reactants
Energetically
unfavourable
Non spontaneous
Mixture
reactant/productEquilibrium
veG  Spontaneous Shift toward
product
79G
33G
6
10G
14
101 
cK
5
105cK
Fe(s) + 3O2(g) ↔ 2Fe2O3(s)
261
101cK
Shift toward
reactants
Energetically
unfavourable
Shift toward
product
Energetically
favourable
Energetically
favourable
Kinetically unfavourable/(stable)
Rate too slow due to HIGH activation energy
Rusting Process
Energy barrier
Shift toward
product
Click here for notes
cellnFEG  
Cell Potential
cellE
0cellE
0cellE
0cellE
0cellE
0cellE
0cellE

16. Eθ
= +0.44V
IB Questions
Esterification produce ethyl ethanoate. ΔG = -4.38kJmol-1 Cal Kc
CH3COOH(l) + C2H5OH(l) ↔ CH3COOC2H5(l) + H2O(l)
Kc = 5.9
cKRTG ln
RT
G
Kc

ln
29831.8
4380
ln


cK
2
?cK
NO oxidized to NO2. Kc = 1.7 x 1012. Cal ∆G at 298K1
3 4
2NO + O2 ↔ NO2 ?G
cKRTG ln
11
12
7.6969772
)107.1ln(298314.8



kJmolJmolG
G
Predict if iron react with HCI in absence air. Cal E cell , ∆G and Kc
Oxidized sp ↔ Reduced sp Eθ/V
Fe2+ + 2e- ↔ Fe -0.44
2H+ + 2e- ↔ H2 0.00
O2 +2H2O+4e ↔ 4OH- +0.40
Fe2+ + 2e- ↔ Fe -0.44
2H+ + 2e- ↔ H2 0.00
О
О
Fe ↔ Fe2+ + 2e Eθ = +0.44
2H+ + 2e ↔ H2 Eθ = 0.00V
Fe + 2H+ → Fe2+ + H2 Eθ = +0.44V
cellnFEG  
kJJG
G
8584900
44.0965002




cKRTG ln 
298314.8
)85000(
ln





RT
G
Kc
14
108.7 cK
∆G –ve, E +ve, K > 1
∆G <0, E > 0, K > 1
↓
Rxn Spontaneous
Fe2+ + 2e- ↔ Fe -0.44
O2 +2H2O+4e ↔ 4OH- +0.40
2Fe ↔ 2Fe2+ + 4e Eθ = +0.44
O2+2H2O+4e ↔ 4OH- Eθ = +0.40
2Fe +O2 +2H2O→2Fe2++4OH- Eθ = +0.84V
Eθ
= +0.84V
Oxidized sp ↔ Reduced sp Eθ/V
Fe2+ + 2e- ↔ Fe -0.44
2H+ + 2e- ↔ H2 0.00
O2 +2H2O+4e ↔ 4OH- +0.40
Predict iron react HCI in presence of air. Cal E cell , ∆G and Kc
О
О
cellnFEG  
kJJG
G
324324000
84.0965004




cKRTG ln 
298314.8
)324000(
ln





RT
G
Kc
56
108.2 cK
∆G –ve, E +ve, K > 1
∆G <0, E > 0, K > 1
↓
Rxn SpontaneousRusting is spontaneous
x 2
О
О
О
О

17. Predict if manganate will oxidize chloride ion?
MnO2 + 4H+ + 2CI- → Mn2+ + 2H2O + CI2
5
MnO2 +4H+ + 2e- ↔ Mn2+ + 2H2O +1.23
1/2CI2 + e- ↔ CI- +1.36
2CI- ↔ CI2 + 2e Eθ = -1.36
MnO2 + 4H+ + 2e ↔ Mn2+ + 2H2O Eθ = +1.23
MnO2 + 4H++2CI- → Mn2++2H2O+CI2 Eθ= -0.13V
Eθ
= -0.13V
Oxidized sp ↔ Reduced sp Eθ/V
Cr2O7
2-+ 14H+ + 6e- ↔ 2Cr3+ + 7H2O +1.33
MnO2 +4H+ + 2e- ↔ Mn2+ + 2H2O +1.23
1/2CI2 + e- ↔ CI- +1.36
MnO4
-
+ 8H+ + 5e- ↔ Mn2+ + 4H2O +1.51
Predict if MnO4
- able to oxidize aq CI- to CI2
2MnO4 + 16H+ + 10CI- → 2Mn2+ + 8H2O + 5CI2
О
О
Oxidized sp ↔ Reduced sp Eθ/V
Cr2O7
2-+ 14H+ + 6e- ↔ 2Cr3+ + 7H2O +1.33
MnO2 +4H+ + 2e- ↔ Mn2+ + 2H2O +1.23
1/2CI2 + e- ↔ CI- +1.36
MnO4
-
+ 8H+ + 5e- ↔ Mn2+ + 4H2O +1.51
О
О
2CI- ↔ CI2 + 2e Eθ = -1.36
MnO4
- + 8H+ + 5e ↔ Mn2+ + 4H2O Eθ = +1.51
2MnO4 + 16H++10CI- → 2Mn2++8H2O+5CI2 Eθ= +0.15V
1/2CI2 + e- ↔ CI- +1.36
MnO4
-
+ 8H+ + 5e- ↔ Mn2+ + 4H2O +1.51
Eθ
= +0.15V
IB Questions
cellnFEG  
kJJG
G
2525000
13.0965002




cKRTG ln 
298314.8
)25000(
ln





RT
G
Kc
5
105.4 
cK
∆G +ve, E -ve, K < 1
∆G >0, E < 0, K < 1
↓
Rxn Non Spontaneous
6
cellnFEG  
kJJG
G
144144750
15.09650010




cKRTG ln 
298314.8
)144000(
ln





RT
G
Kc
25
105.1 cK
∆G –ve, E +ve, K > 1
∆G <0, E > 0, K > 1
↓
Rxn Spontaneous
x 5
x 2
О
О
О
О

18. Acknowledgements
Thanks to source of pictures and video used in this presentation
Thanks to Creative Commons for excellent contribution on licenses
http://creativecommons.org/licenses/
Prepared by Lawrence Kok
Check out more video tutorials from my site and hope you enjoy this tutorial
http://lawrencekok.blogspot.com