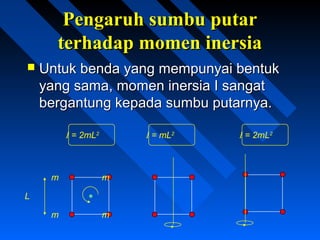
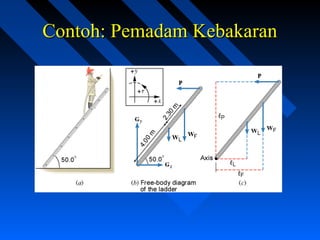
Dokumen ini membahas konsep dinamika rotasi, termasuk definisi dan hukum torsi, momen inersia, serta kondisi kesetimbangan benda tegar. Ia menjelaskan pentingnya memilih sumbu rotasi yang tepat dan menerapkan persamaan kesetimbangan gaya dan torsi. Selain itu, dokumen ini mencakup contoh penerapan hukum fisika dalam situasi nyata, seperti pemadam kebakaran dan gerak silinder.

1. DINAMIKA ROTASIDINAMIKA ROTASI

2. Efek Dari Gaya Dan TorsiEfek Dari Gaya Dan Torsi
Terhadap Gerak BendaTerhadap Gerak Benda

3. TorsiTorsi
 DEFINISIDEFINISI
Torsi merupakan hasil kali besarnya gayaTorsi merupakan hasil kali besarnya gaya
dengan panjangnya lengan.dengan panjangnya lengan.
 Torsi berarah positif apabila gayaTorsi berarah positif apabila gaya
menghasilkan rotasi yang berlawananmenghasilkan rotasi yang berlawanan
dengan arah jarum jam.dengan arah jarum jam.
 Satuan SI dari Torsi: newton.m (N.m)Satuan SI dari Torsi: newton.m (N.m)
F=τ

4. Hukum Ii Newton UntukHukum Ii Newton Untuk
RotasiRotasi
 Hukum kedua Newton untuk rotasiHukum kedua Newton untuk rotasi
sebuah benda tegar melalui sumbusebuah benda tegar melalui sumbu
yang tetap adalah:yang tetap adalah:
ατ I=netto
 Dengan I merupakan momen inersiaDengan I merupakan momen inersia
dari sistem partikel yang didefinisikandari sistem partikel yang didefinisikan
sebagai berikut:sebagai berikut:
∑=
i
iirmI 2

5. Contoh Menghitung MomenContoh Menghitung Momen
InersiaInersia
Hitung momen inersiaHitung momen inersia
dari empat titik massadari empat titik massa
((mm) yang terletak pada) yang terletak pada
sudut-sudut suatusudut-sudut suatu
bujursangkar yangbujursangkar yang
masing-masing sisinyamasing-masing sisinya
mempunyai panjangmempunyai panjang LL..
mm
mm
L

6. SolusiSolusi
 Kuadrat jarak dari masing-masing titikKuadrat jarak dari masing-masing titik
massa terhadap sumbu putar adalah:massa terhadap sumbu putar adalah:
 SehinggaSehingga
22
2
22
2 LL
r =




=
2
4
2222
I
22222
1
2 L
m
L
m
L
m
L
m
L
mrm
N
i
ii =+++== ∑
=
2
2mLI =

7. Pengaruh sumbu putarPengaruh sumbu putar
terhadap momen inersiaterhadap momen inersia
 Untuk benda yang mempunyai bentukUntuk benda yang mempunyai bentuk
yang sama, momen inersia I sangatyang sama, momen inersia I sangat
bergantung kepada sumbu putarnya.bergantung kepada sumbu putarnya.
I = 2mL2
I = mL2
L
mm
mm
I = 2mL2

8. Teorema Sumbu SejajarTeorema Sumbu Sejajar
 Andaikan momen inersia dari suatu bendaAndaikan momen inersia dari suatu benda
bermassabermassa MM pada suatu sumbu putar yangpada suatu sumbu putar yang
melewati pusat massa diketahui adalahmelewati pusat massa diketahui adalah IICMCM
 Momen inersia pada suatu sumbu paralelMomen inersia pada suatu sumbu paralel
dari sumbu putar pusat massa dan berjarakdari sumbu putar pusat massa dan berjarak
sejauhsejauh DD adalah:adalah:
IIPARALELPARALEL = I= ICMCM + MD+ MD22

9. Kesetimbangan Benda TegarKesetimbangan Benda Tegar

10.  Suatu benda tegar dikatakan setimbangSuatu benda tegar dikatakan setimbang
apabila memiliki percepatan translasi samaapabila memiliki percepatan translasi sama
dengan nol dan percepatan sudut samadengan nol dan percepatan sudut sama
dengan nol.dengan nol.
 Dalam keadaan setimbang, seluruh resultanDalam keadaan setimbang, seluruh resultan
gaya yang bekerja harus sama dengan nol,gaya yang bekerja harus sama dengan nol,
dan resultan torsi yang bekerja juga harusdan resultan torsi yang bekerja juga harus
sama dengan nol:sama dengan nol:
ΣΣFFxx = 0= 0 dandan ΣΣFFyy = 0= 0
ΣΣττ = 0= 0
Kesetimbangan Benda TegarKesetimbangan Benda Tegar

11. Strategi Untuk Menerapkan KondisiStrategi Untuk Menerapkan Kondisi
KesetimbanganBenda TegarKesetimbanganBenda Tegar
1.1. Pilih benda dimana persamaan kesetim-Pilih benda dimana persamaan kesetim-
bangan akan dipergunakan.bangan akan dipergunakan.
2.2. Gambarkan diagram benda bebas yangGambarkan diagram benda bebas yang
menunjukkan seluruh gaya eksternal yangmenunjukkan seluruh gaya eksternal yang
bekerja pada benda.bekerja pada benda.
3.3. Pilihlah sumbuPilihlah sumbu xx dandan yy yang akanyang akan
memudahkan kita dalam menyelesaikanmemudahkan kita dalam menyelesaikan
permasalahan.permasalahan.

12. 4.4. Terapkan persamaan yang menunjukkanTerapkan persamaan yang menunjukkan
kesetimbangan gaya:kesetimbangan gaya: ΣΣFFxx = 0 and= 0 and ΣΣFFyy = 0= 0
5.5. Pilihlah sumbu rotasi yang tepat. Iden-Pilihlah sumbu rotasi yang tepat. Iden-
tifikasi titik dimana tiap gaya eksternaltifikasi titik dimana tiap gaya eksternal
yang bekerja pada benda dan hitunglahyang bekerja pada benda dan hitunglah
torsi yang dikerjakan oleh gaya tersebuttorsi yang dikerjakan oleh gaya tersebut
terhadap sumbu rotasi tadi.terhadap sumbu rotasi tadi.
ΣΣττ = 0.= 0.
 Carilah apa yang belum diketahui dariCarilah apa yang belum diketahui dari
persoalannyapersoalannya
Strategi Untuk Menerapkan KondisiStrategi Untuk Menerapkan Kondisi
KesetimbanganBenda TegarKesetimbanganBenda Tegar

13. Contoh: Pemadam KebakaranContoh: Pemadam Kebakaran
 Pada gambar tampak seorang pemadamPada gambar tampak seorang pemadam
kebakaran sedang berdiri di atas sebuahkebakaran sedang berdiri di atas sebuah
tangga yang panjangnya 8 m dan beratnyatangga yang panjangnya 8 m dan beratnya
WWLL = 355 N yang menyandar pada sebuah= 355 N yang menyandar pada sebuah
dinding licin. Orang tersebut memiliki beratdinding licin. Orang tersebut memiliki berat
WWFF = 875 N, berdiri pada jarak 6,3 m dari= 875 N, berdiri pada jarak 6,3 m dari
ujung bawah tangga. Jika pusat massaujung bawah tangga. Jika pusat massa
tangga tepat berada di tengah, carilah gayatangga tepat berada di tengah, carilah gaya
pada dinding dan tanah yang disebabkanpada dinding dan tanah yang disebabkan
oleh tangga.oleh tangga.

14. Contoh: Pemadam KebakaranContoh: Pemadam Kebakaran

15. SolusiSolusi
 GayaGaya PP adalah gaya yang diberikan olehadalah gaya yang diberikan oleh
ujung atas tangga kepada dinding.ujung atas tangga kepada dinding.
 GayaGaya GGxx dandan GGyy merupakan gaya yang bekerjamerupakan gaya yang bekerja
pada ujung bawah tangga.pada ujung bawah tangga.
 Dengan menetapkan persamaan kesetimba-Dengan menetapkan persamaan kesetimba-
ngan benda tegar diperoleh:ngan benda tegar diperoleh:

16.  Perhitungan torsi untuk sistem diatas adalahPerhitungan torsi untuk sistem diatas adalah
sebagai berikut:sebagai berikut:
SolusiSolusi

17.  Dari persamaan tadi, diperoleh hasil:Dari persamaan tadi, diperoleh hasil:
SolusiSolusi

18. Kerja RotasiKerja Rotasi
 DEFINISIDEFINISI
Kerja rotasi WKerja rotasi WRR dilakukan oleh torsi konstandilakukan oleh torsi konstan
ττ yang berputar dengan sudutyang berputar dengan sudut θθ..
 θθ harus dalam radianharus dalam radian
 Satuan SI untuk kerja rotasi adalah joule (J)Satuan SI untuk kerja rotasi adalah joule (J)
τθ=RW

19. Energi Kinetik RotasiEnergi Kinetik Rotasi
 DEFINISIDEFINISI
Energi kinetik rotasi dari suatu benda tegarEnergi kinetik rotasi dari suatu benda tegar
yang berotasi dengan kecepatan sudutyang berotasi dengan kecepatan sudut ωω didi
seputar sumbu tetap dan memiliki momenseputar sumbu tetap dan memiliki momen
inersiainersia II adalah:adalah:
 ωω harus dalam rad/sharus dalam rad/s
2
2
1
ωIEKR =

20. Hukum Kekekalan Energi MekanikHukum Kekekalan Energi Mekanik
Total Dengan Gerak RotasiTotal Dengan Gerak Rotasi

21. Hukum Kekekalan Energi MekanikHukum Kekekalan Energi Mekanik
Total Dengan Gerak RotasiTotal Dengan Gerak Rotasi

22. Contoh : Silinder Yang BergerakContoh : Silinder Yang Bergerak
Sebuah silinder kosong (massa =
mh, jari-jari = rh) dan silinder pejal
(massa = ms, jari-jari rs)
menggelinding dari keadaan diam
di puncak sebuah bidang miring.
Kedua silinder berada di ketinggian
yang sama h0. Abaikan energi yang
hilang selama gerak
menggelinding. Tentukan silinder
yang mana yang memiliki
kecepatan translasi terbesar ketika
mencapai dasar dari bidang miring.

23. SolusiSolusi
• Hanya gaya gravitasi yang merupakan gaya
konservatif yang bekerja pada silinder. Sehingga
energi mekanik total konservatif selama gerak
menggelinding turun ke bawah.
• Total energi mekanik Ef
di bawah (hf
= 0) sama
dengan total energi mekanik E0
di atas
• Sehingga:
0
2
02
12
02
12
2
12
2
1 mghImvmghImv fff ++=++ ωω
0
2
2
12
2
1 mghImv ff =+ ω

24.  Karena silinder menggelinding tanpa slip dan
gerak silinder dapat ditinjau dengan gerak pusat
massa, maka:
• Sehingga diperoleh:
SolusiSolusi
r
vf
f =ω
( )2
0
/
2
rIm
mgh
vf
+
=

25.  Untuk silinder kosong,
 Untuk silinder pejal,
SolusiSolusi
2
; hhh rmImm == 0ghvf =⇒
2
2
1; sss rmImm ==
3
4 0gh
vf =⇒

26. Momentum SudutMomentum Sudut

27.  DEFINISIDEFINISI
Momentum sudut dari sebuah benda yangMomentum sudut dari sebuah benda yang
berotasi tehadap sumbu tetap adalah hasilberotasi tehadap sumbu tetap adalah hasil
kali dari momen inersia benda dengankali dari momen inersia benda dengan
kecepatan sudut terhadap sumbu rotasikecepatan sudut terhadap sumbu rotasi
tersebut.tersebut.
 Satuan SI untuk momentum sudutSatuan SI untuk momentum sudut
kg.mkg.m22
/s/s
Momentum SudutMomentum Sudut
ωIL =

28. Hukum Kekekalan Momentum SudutHukum Kekekalan Momentum Sudut
 Momentum sudut dari suatu sistemMomentum sudut dari suatu sistem
dikatakan kekal apabila resultan torsi luardikatakan kekal apabila resultan torsi luar
yang bekerja pada sistem adalah nol.yang bekerja pada sistem adalah nol.

29. Applet untuk Dinamika RotasiApplet untuk Dinamika Rotasi