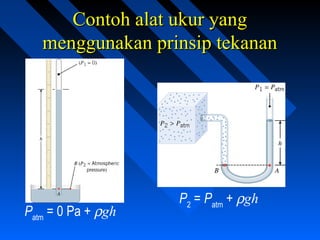
Dokumen ini membahas tentang statika dan dinamika fluida, termasuk konsep kerapatan, tekanan, dan hukum-hukum yang berhubungan seperti Prinsip Pascal dan Prinsip Archimedes. Contoh-contoh aplikatif dan perhitungan terkait kerapatan dan gaya apung juga disediakan. Selain itu, dokumen ini menjelaskan persamaan kontinuitas dan persamaan Bernoulli dalam analisis aliran fluida.

1. FLUIDAFLUIDA

2. STATIKA FLUIDASTATIKA FLUIDA
 Kerapatan zat cair.Kerapatan zat cair.
 Tekanan.Tekanan.
 Hubungan antara tekanan danHubungan antara tekanan dan
kedalaman pada statika fluida.kedalaman pada statika fluida.
 Hukum-Hukum HidrostatikaHukum-Hukum Hidrostatika
 Prinsip PascalPrinsip Pascal
 Prinsip ArchimedesPrinsip Archimedes

3. KerapatanKerapatan
 DefinisiDefinisi
KerapatanKerapatan ρρ adalah massaadalah massa mm dibagi dengandibagi dengan
volumevolume VV
V
m
=ρ
Satuan dari kerapatan (SI) adalah kg/m3

4. Contoh : KerapatanContoh : Kerapatan
 Tubuh manusia dengan berat 690 N mengandungTubuh manusia dengan berat 690 N mengandung
5,2 x 105,2 x 10-3-3
mm33
darah.darah.
(a) Tentukan berat dari darah ((a) Tentukan berat dari darah (ρρdarahdarah = 1060 kg/m= 1060 kg/m3)3)
..
(b) Tuliskan berat tersebut dalam persentase(b) Tuliskan berat tersebut dalam persentase
terhadap berat manusia tersebut.terhadap berat manusia tersebut.
Jawab:Jawab:
a)a) mm == ρρVV →→ mm = (1060)(5,2x10= (1060)(5,2x10-3-3
) = 5,5 kg) = 5,5 kg
W = mgW = mg →→ W =W = (5,5)(10) = 55 kg(5,5)(10) = 55 kg
b) Persentase = (55)/(690)b) Persentase = (55)/(690) ≈≈ 8%8%

5. TEKANANTEKANAN
 DEFINISIDEFINISI
Tekanan adalah gaya per satuan luas yangTekanan adalah gaya per satuan luas yang
dikerjakan oleh fluida tersebut.dikerjakan oleh fluida tersebut.
A
F
P =
Satuan dari tekanan (SI) adalah Pascal (Pa)
1 atm = 101,3245 kPa = 760 mmHg = 760 torr
Tekanan gauge adalah perbedaan tekanan
absolut dan tekanan atmosfer.

6. Hubungan Antara Tekanan DanHubungan Antara Tekanan Dan
Kedalaman Pada Statika FluidaKedalaman Pada Statika Fluida
 Semakin dalam seorang penyelamSemakin dalam seorang penyelam
menyelam di dalam suatu cairan semakinmenyelam di dalam suatu cairan semakin
kuat cairan tsb. mene-kan tubuhnya dankuat cairan tsb. mene-kan tubuhnya dan
semakin besar tekanan yang dialaminya.semakin besar tekanan yang dialaminya.
 Untuk menemukan hubungan antaraUntuk menemukan hubungan antara
tekanan dan kedalaman, maka diterapkantekanan dan kedalaman, maka diterapkan
Hukum II Newton terhadap suatu elemenHukum II Newton terhadap suatu elemen
volume cairan.volume cairan.

7. Hubungan Antara Tekanan Dan KedalamanHubungan Antara Tekanan Dan Kedalaman
Pada Statika Fluida (Lanjutan)Pada Statika Fluida (Lanjutan)
012 =−−=∑ mghAPAPFy
mghAPAP +=→ 12
hAVm ρρ ==
Tetapi
sehingga
ghPP ρ+= 12

8. Hubungan Antara Tekanan Dan KedalamanHubungan Antara Tekanan Dan Kedalaman
Pada Statika Fluida (Lanjutan)Pada Statika Fluida (Lanjutan)
Tekanan pada sembarang
titik di dalam suatu cairan
bergantung kepada jarak
vertikal h yaitu kedalaman
titik tersebut terhadap
permukaan cairan.

9. Gaya Pada Dinding Sebuah DamGaya Pada Dinding Sebuah Dam
SegiempatSegiempat
luardiudaraatasdiudaraairR FFFF −+=
[ ] ( )[ ] [ ]whPdhwPdywP oo
d
y −−+= ∫
0
.
( ) [ ] wdPdywgyP o
d
o −+= ∫
0
..ρ
2
0 2
1
.. gwddyygw
d
ρρ == ∫

10. Prinsip PascalPrinsip Pascal
 Tekanan yang bekerja pada cairan tertutupTekanan yang bekerja pada cairan tertutup
diteruskan tanpa berkurang ke tiap titikditeruskan tanpa berkurang ke tiap titik
dalam fluida dan ke dinding wadah.dalam fluida dan ke dinding wadah.
12 PP =






=⇒=
1
2
12
1
1
2
2
A
A
FF
A
F
A
F

11. Contoh Pemakaian Prinsip PascalContoh Pemakaian Prinsip Pascal
 Sebuah pengungkit mobil hidrolikSebuah pengungkit mobil hidrolik
piston 1 memiliki jari-jari 0,0120 mpiston 1 memiliki jari-jari 0,0120 m
dan massanya dapat diabaikan. Pistondan massanya dapat diabaikan. Piston
2 memiliki jari-jari 0,150 m. Berat dari2 memiliki jari-jari 0,150 m. Berat dari
mobil dan piston 2 adalah 20.500 N.mobil dan piston 2 adalah 20.500 N.
Pengungkit ini menggunakan oliPengungkit ini menggunakan oli
dengan kerapatan 8x10dengan kerapatan 8x1022
kg/mkg/m33
. Berapa. Berapa
gaya Fgaya F11 yang diperlukan untukyang diperlukan untuk
menopang mobil dan piston 2 jikamenopang mobil dan piston 2 jika
permukaan bawah dari piston 1 danpermukaan bawah dari piston 1 dan
piston 2:piston 2:
a) samaa) sama
b) memiliki perbedaan ketinggianb) memiliki perbedaan ketinggian
seperti gambar denganseperti gambar dengan hh = 1,1 m= 1,1 m

12. SolusiSolusi
a) Dengan menggunakan A = πr2
, diperoleh:








=





= 2
2
2
1
2
2
1
21
r
r
F
A
A
FF
π
π
( ) N131
150,0
012,0
20500 2
2
=







=
b) Karena ketinggian dasar kedua piston tidak sama
maka P2
= P1
+ ρgh
sehingga ( )2
12
2
2
1
21 rgh
r
r
FF πρ−







= N127=

13. Contoh alat ukur yangContoh alat ukur yang
menggunakan prinsip tekananmenggunakan prinsip tekanan
P2
= Patm
+ ρgh
Patm
= 0 Pa + ρgh

14. Prinsip ArchimedesPrinsip Archimedes
 Jika kita berusaha mendorong bola ke dalam suatuJika kita berusaha mendorong bola ke dalam suatu
cairan maka akan dirasakan bahwa cairan akancairan maka akan dirasakan bahwa cairan akan
mendorong bola kembali ke atas dengan suatumendorong bola kembali ke atas dengan suatu
gaya, gaya tersebut disebut gaya apung.gaya, gaya tersebut disebut gaya apung.
Sebuah benda yang seluruhnya atau
sebagian tercelup dalam fluida
diapungkan ke atas oleh gaya yang
sama dengan berat fluida yang
dipindahkan.
Definisi
cairanB WF =

15.  Sebuah papan kayu (Sebuah papan kayu (ρρ = 550 kg/m= 550 kg/m33
))
bujur sangkar dengan panjang sisi 4 mbujur sangkar dengan panjang sisi 4 m
dan tebal 0,3 m.dan tebal 0,3 m.
(a) Tentukan apakah papan tersebut(a) Tentukan apakah papan tersebut
mengapung di air ayau tidak?mengapung di air ayau tidak?
(b) Jika mengapung, berapa bagiankah(b) Jika mengapung, berapa bagiankah
tebal papan tsb. yang terbenam dalam airtebal papan tsb. yang terbenam dalam air
Jawab:Jawab:
(a)(a) Berat dari papan = (Berat dari papan = (ρρpapanpapan VVpapanpapan))gg
= (550)(4,8)(9,8) = 26000 N= (550)(4,8)(9,8) = 26000 N
Gaya apung maksimum = (Gaya apung maksimum = (ρρairair VVpapanpapan))gg
== (1000)(4,8)(9,8) = 47 000 N(1000)(4,8)(9,8) = 47 000 N
(b)(b) ( )ghW aircairan x4x426000 ρ==
( )( )8,94x4)1000(
26000
=h m17,0=

16. Dinamika FluidaDinamika Fluida
 Fluida yang mengalir dapat memiliki keadaan:Fluida yang mengalir dapat memiliki keadaan:
– Tunak dan tidak tunakTunak dan tidak tunak
– Kompresibel dan tiak kompresibelKompresibel dan tiak kompresibel
– Kental dan tidak kentalKental dan tidak kental
– Rotasional dan tidak rotasionalRotasional dan tidak rotasional
 Untuk fluida ideal, maka diasumsikan bahwaUntuk fluida ideal, maka diasumsikan bahwa
keadaan fluida tersebut adalah tunak, tidakkeadaan fluida tersebut adalah tunak, tidak
kompresibel, tidak kental dan tidak rotasional.kompresibel, tidak kental dan tidak rotasional.

17. StreamlinesStreamlines
 Ketika aliran dalam keadaan tunak,Ketika aliran dalam keadaan tunak,
streamlines biasanya sering digunakanstreamlines biasanya sering digunakan
untuk menunjukkan jejak dari partikeluntuk menunjukkan jejak dari partikel
fluida. Streamline adalah garis-garis padafluida. Streamline adalah garis-garis pada
fluida, sehingga garis singgung padafluida, sehingga garis singgung pada
streamline tersebut di setiap titik searahstreamline tersebut di setiap titik searah
dengan kecepatan fluida pada titik tersebut.dengan kecepatan fluida pada titik tersebut.
 Aliran tunak seringkali disebut sebagaiAliran tunak seringkali disebut sebagai
aliran streamline.aliran streamline.

18. Persamaan KontinuitasPersamaan Kontinuitas
 Jika fluida memasuki suatu pipa dengan lajuJika fluida memasuki suatu pipa dengan laju
yang tetap maka fluida tersebut juga harusyang tetap maka fluida tersebut juga harus
meninggal pipa tersebut dengan laju yangmeninggal pipa tersebut dengan laju yang
sama, asumsikan bahwa tidak adasama, asumsikan bahwa tidak ada
kebocoran pada dinding pipa. Aliran massakebocoran pada dinding pipa. Aliran massa
fluida per detik yang melewati pipa disebutfluida per detik yang melewati pipa disebut
laju aliran massa.laju aliran massa.

19.  Laju aliran massa (Laju aliran massa (ρρAvAv) memilik nilai yang) memilik nilai yang
sama di setiap posisi sepanjang pipa yangsama di setiap posisi sepanjang pipa yang
memiliki satu titik masuk dan satu titik keluarmemiliki satu titik masuk dan satu titik keluar
untuk aliran fluida. Untuk dua posisi diuntuk aliran fluida. Untuk dua posisi di
sepanjang pipa berlaku:sepanjang pipa berlaku:
ρρ11AA11vv11 == ρρ22AA22vv22
 DenganDengan ρρ = rapat massa fluida(kg/m= rapat massa fluida(kg/m33
))
 AA = Luas penampang lintang dari pipa (m= Luas penampang lintang dari pipa (m22
))
 vv = laju fluida (m/s)= laju fluida (m/s)
Persamaan KontinuitasPersamaan Kontinuitas

20.  Untuk fluida ideal, berlakuUntuk fluida ideal, berlaku ρρ11 == ρρ22 sehingga:sehingga:
AA11vv11 == AA22vv22
 KuantitasKuantitas AvAv menunjukkan laju aliranmenunjukkan laju aliran
volume dari fluida.volume dari fluida.
QQ = laju aliran volume == laju aliran volume = AvAv
Persamaan KontinuitasPersamaan Kontinuitas

21. Persamaan BernoulliPersamaan Bernoulli

22. Persamaan BernoulliPersamaan Bernoulli

23.  Ketika fluida mengalir dalam pipaKetika fluida mengalir dalam pipa
horisontal dan memasuki pipa yanghorisontal dan memasuki pipa yang
memiliki penampang lintang mengecil,memiliki penampang lintang mengecil,
tekanan dari fluida menjadi lebih kecil.tekanan dari fluida menjadi lebih kecil.
Persamaan BernoulliPersamaan Bernoulli

24. Persamaan BernoulliPersamaan Bernoulli

25.  Dalam aliran yang tunak, tidak kental, danDalam aliran yang tunak, tidak kental, dan
tiak kompresible fluida dengan rapat massatiak kompresible fluida dengan rapat massa
ρρ, tekanan, tekanan PP, kecepatan, kecepatan vv dan ketinggiandan ketinggian yy
dihitung dari dua titik (1 dan 2) terkaitandihitung dari dua titik (1 dan 2) terkaitan
dengan persamaan:dengan persamaan:
 Tetapi nilai tersebut tetap untuk setiapTetapi nilai tersebut tetap untuk setiap
posisi dalam aliran sehingga:posisi dalam aliran sehingga:
PP + ½+ ½ ρρ vv22
++ ρρgygy = konstan= konstan
Persamaan BernoulliPersamaan Bernoulli
2
2
221
2
11
2
1
2
1
gyvPgyvP ρρρρ ++=++

26. Applet tentang FluidaApplet tentang Fluida