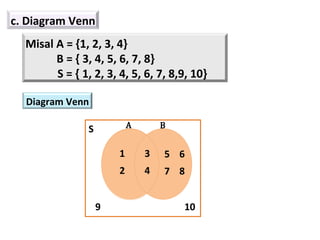
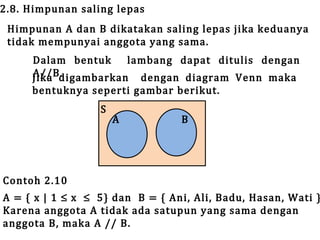
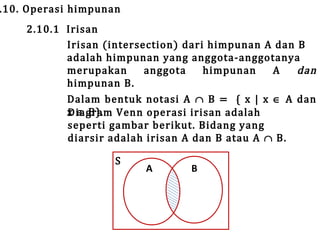
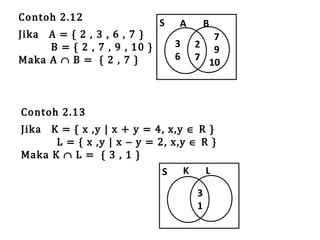
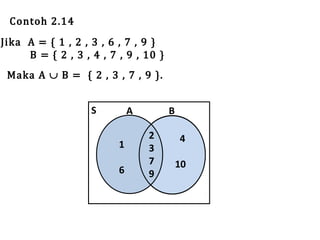
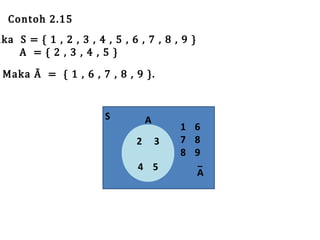
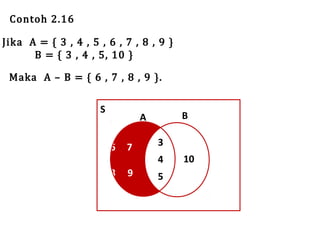
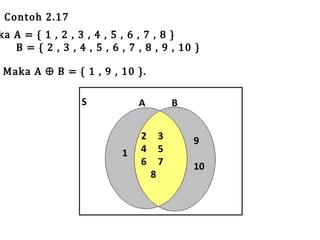
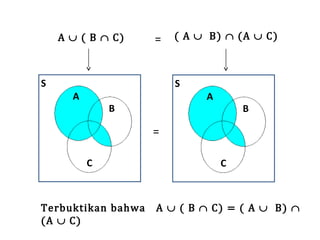
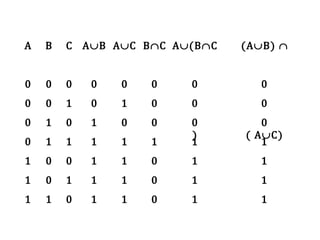
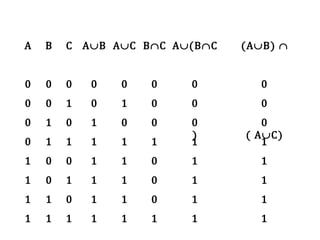
Teks tersebut membahas tentang definisi dan penyajian himpunan, termasuk tabulasi, notasi pembentuk himpunan, diagram Venn, kardinalitas, himpunan kosong, subset, kesamaan, ekivalensi, saling lepas, himpunan kuasa, dan berbagai operasi himpunan seperti irisan, gabungan, komplemen, selisih, beda setangkup, perkalian Kartesian, dan prinsip inklusi-eksklusi.