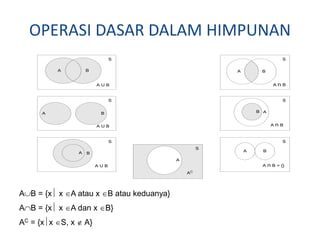
Dokumen ini membahas teori himpunan, yang mencakup definisi himpunan, anggota, penulisan himpunan, dan berbagai jenis himpunan seperti himpunan kosong dan himpunan semesta. Selain itu, dijelaskan juga hubungan antar himpunan, operasi dasar seperti gabungan, irisan, dan komplemen, serta notasi-notasi yang digunakan dalam teori himpunan. Contoh-contoh konkret diberikan untuk memperjelas konsep-konsep yang dibahas.

1. TEORI HIMPUNAN
 Himpunan adalah kumpulan obyek
 Obyek dalam sebuah himpunan disebut anggota atau unsur
atau elemen
 Penulisan himpunan
 Listing Method
 Description Method
 Listing Method
A = {1, 2, 3, 4, 5, 6}
 Description Method (notasi pembentuk himpunan)
A = {x | 1  x  6 ; x bilangan bulat}

2. NOTASI HIMPUNAN
 A = {1, 2, 3, 4, 5, 6}
 1  A, 2  A, 3  A, 4  A, 5  A, 6  A
  = anggota himpunan
  = bukan anggota himpunan
 7  A, 8  A, 10  A.
 A  B,  = himpunan bagian
 |A| = banyaknya anggota himpunan A, atau n(A)
A = {a,b,c,d,e,f} ; |A| = 6;

3.  Himpunan yang tidak mengandung
anggota dinamakan himpunan kosong
;
 Dilambangkan dengan  atau { }
 Contoh: A= {}
 Himpunan kosong adalah himpunan
bagian dari setiap himpunan.
HIMPUNAN KOSONG

4. DIAGRAM VENN DAN HIMPUNAN
SEMESTA
• Himpunan semesta: Himpunan yang memuat
semua anggota yang dibicarakan, disebut juga
semesta pembicaraan
• Contoh:
S = semesta hewan
A = hewan berkaki empat
A = {kambing, sapi, kuda}
SA
.
kambing
. sapi
. kuda
.
ayam
. bebek

5. HUBUNGAN ANTAR HIMPUNAN
• Himpunan Bagian
• Himpunan saling lepas (disjoin)
• Himpunan saling berpotongan

6. HIMPUNAN BAGIAN
 Definisi himpunan bagian : Jika setiap anggota
himpunan A adalah juga anggota himpunan B ; A  B
 Himpunan A = B jika dan hanya jika A  B dan B  A
 Jika A dan B adalah himpunan, sedemikian rupa
sehingga A  B tetapi A  B, maka A adalah proper
subset dari himpunan B;
A  B
contoh: A={1,2,3,4,5}; B={1,2,3}; maka B  A

7. HIMPUNAN SALING LEPAS
Bila v x  A ≠ v x  B (himpunan A
tidak memiliki anggota yang sama dengan
himpunan B)
SA B

8. HIMPUNAN SALING BERPOTONGAN
• Bila x  A = x  B
• Ada anggota himpunan A yang juga anggota
himpunan B
SA B

9. OPERASI DASAR DALAM HIMPUNAN
 Operasi dasar himpunan:
 Gabungan (union); 
A  B = {x | x  A dan x  B}
 Irisan (intersection); 
A  B = {x | x  A atau x  B}
 Komplemen (complement); c
Ac = {x | x  S; x  A}

10. S
A B
A U B
S
A B
A n B
S
A n B
AB
S
A U B
BA
S
A n B = {}
BA
S
A U B
BA
S
AC
A
AB = {x x A atau x B atau keduanya}
AB = {x x A dan x B}
AC = {xx S, x  A}
OPERASI DASAR DALAM HIMPUNAN

11. TERIMA KASIH