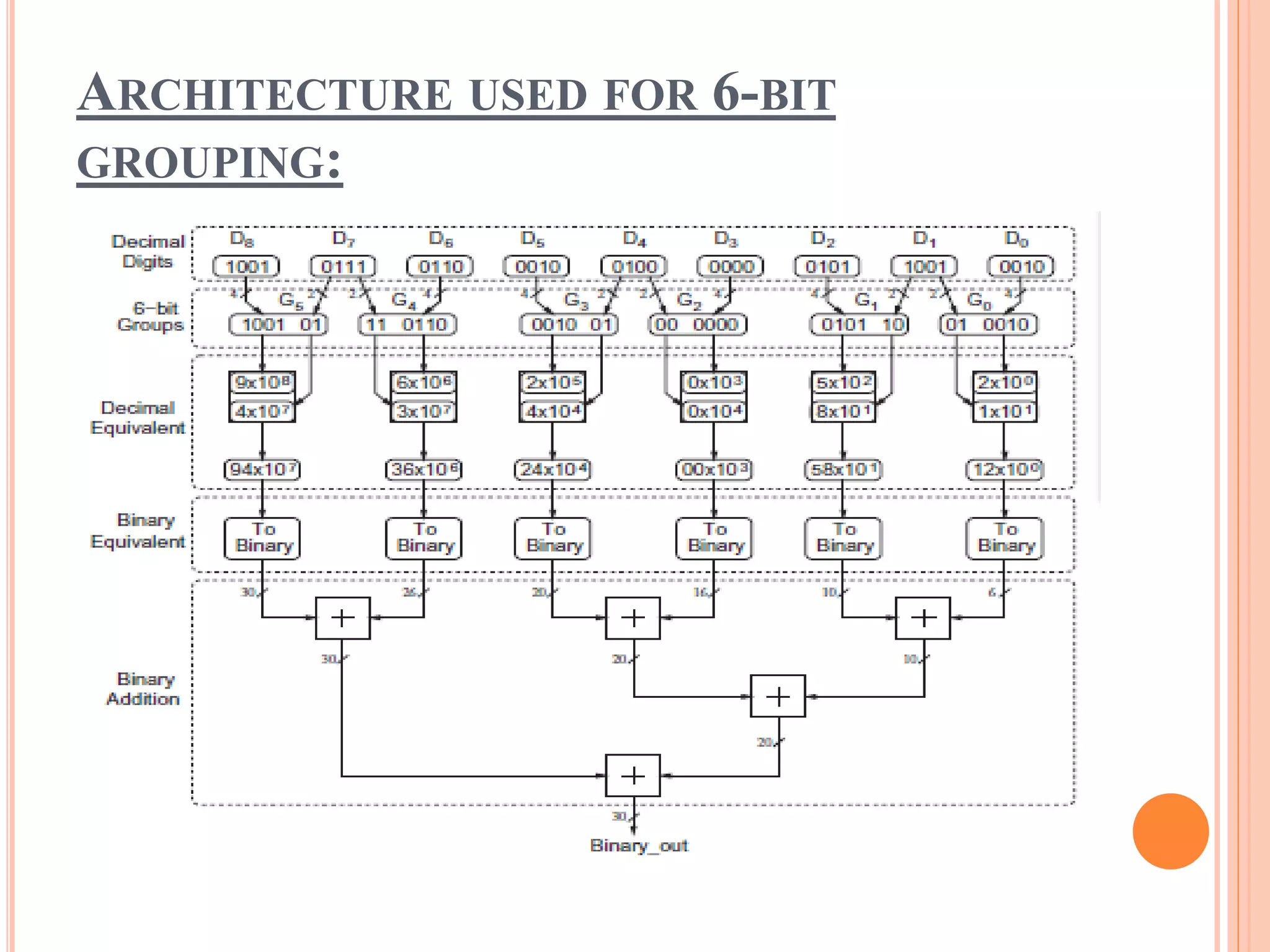
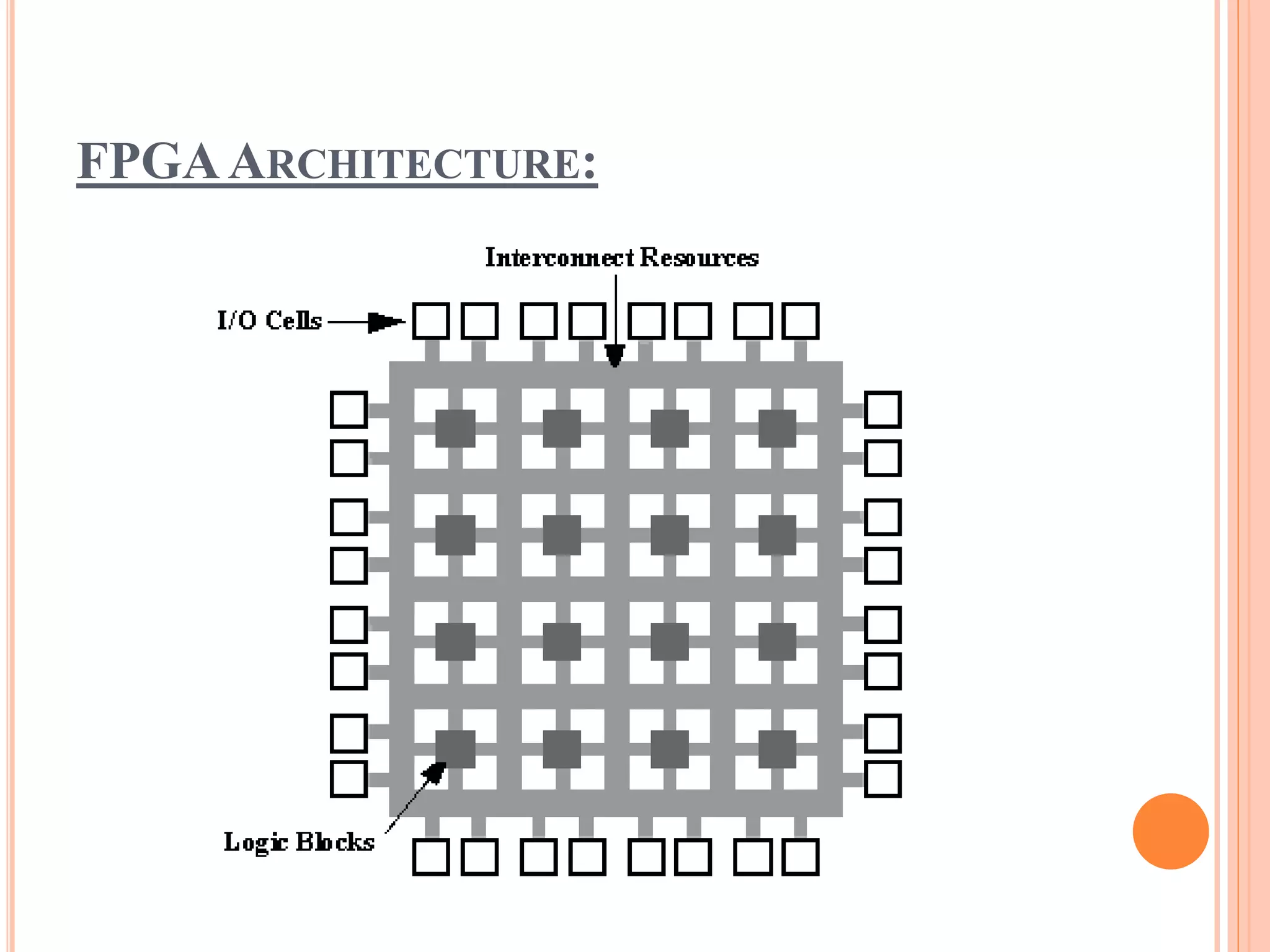
This document presents high-performance FPGA-based schemes for converting decimal to binary, employing bit-grouping techniques to enhance decimal arithmetic efficiency. It emphasizes the advantages of using shifters to reduce delays and improve performance in financial and scientific applications. The proposed architecture requires fewer look-up tables (LUTs) and demonstrates reduced delay compared to traditional methods.

1. HIGH PERFORMANCE FPGA-BASED DECIMAL-
TO-BINARY CONVERSION SCHEMES
FOR DECIMAL ARITHMETIC

2. TABLE OF CONTENTS:
 Introduction
 Bit- grouping
 Techniques used for bit-grouping
 FPGA architecture
 FPGA implementation
 Applications
 Tool used
 Conclusion
 Proposed work

3. INTRODUCTION :
 High performance architecture for decimal to binary
conversion to support decimal arithmetic .
 First split the BCD input into several groups of bits and
then compute the contribution of each group to the final
result .
 Add the contributions to form the final result.

4. High performance
depends
Area
Delay
Power

5. WHY WE ARE USING DECIMAL
ARITHMETIC?
 Decimal arithmetic has gained high impact on the overall
performance of today’s financial, scientific and
commercial applications.
 Decimal operand reduces potential rounding errors and
direct manipulation of these decimal numbers might
promise better performance.

6. BCD TO BINARY CONVERSION
 BCD number 76 is expanded to
(7 x10 + 6 x 1 = 7 x (8 + 2) + 6 x 1 = 7 x 23 + 7 x 21 + 6 x
20)
This means that the binary equivalent of the BCD
number 76 can be obtained by the addition of 7 shifted to
the left 3 times (0111000)2, 7 shifted to the left 1 time
(01110)2, and 6 not shifted (0110)2.
The binary result is (0111000)2 + (01110)2 + (0110)2=
(1001100)2.

7. WHY WE ARE USING SHIFTERS?
There is very large delay in multipliers so
we are using shifters.
 Shifters reduces delays which improves
the performance of decimal to binary
conversion.

8. BIT GROUPING
 Our Architecture is based on bit grouping.
 Bit-grouping is based on splitting the input BCD number
into groups of consecutive bits from the least significant
position to the most significant position.

9. GENERAL ARCHITECTURE FOR 4-BIT
GROUPING
CONTINUED….

10.  WD0 is used to represent the size of the output of
the D0 contribution generator unit.
 WD1 is used to represent the size of the output of
the D1 contribution generator unit, and so on.
 The BCD input size is N BCD digits, DN1 DN2 D1
D2, each digit is fed to its corresponding
contribution generator unit that computes the
contribution of that digit to the final binary result.

11. TECHNIQUES USED FOR BIT-
GROUPING:
i ) 4-bit grouping
ii) 6-bit grouping
iii) 8-bit grouping

12. 4-BIT GROUPING:
 In this grouping the size of each group is 4 bits i.e.
1BCD digit .
 For example, a (5)10 = (0101)BCD contributes
(0101)2 to the final binary result.

13. ARCHITECTURE USED FOR 4-BIT
GROUPING:

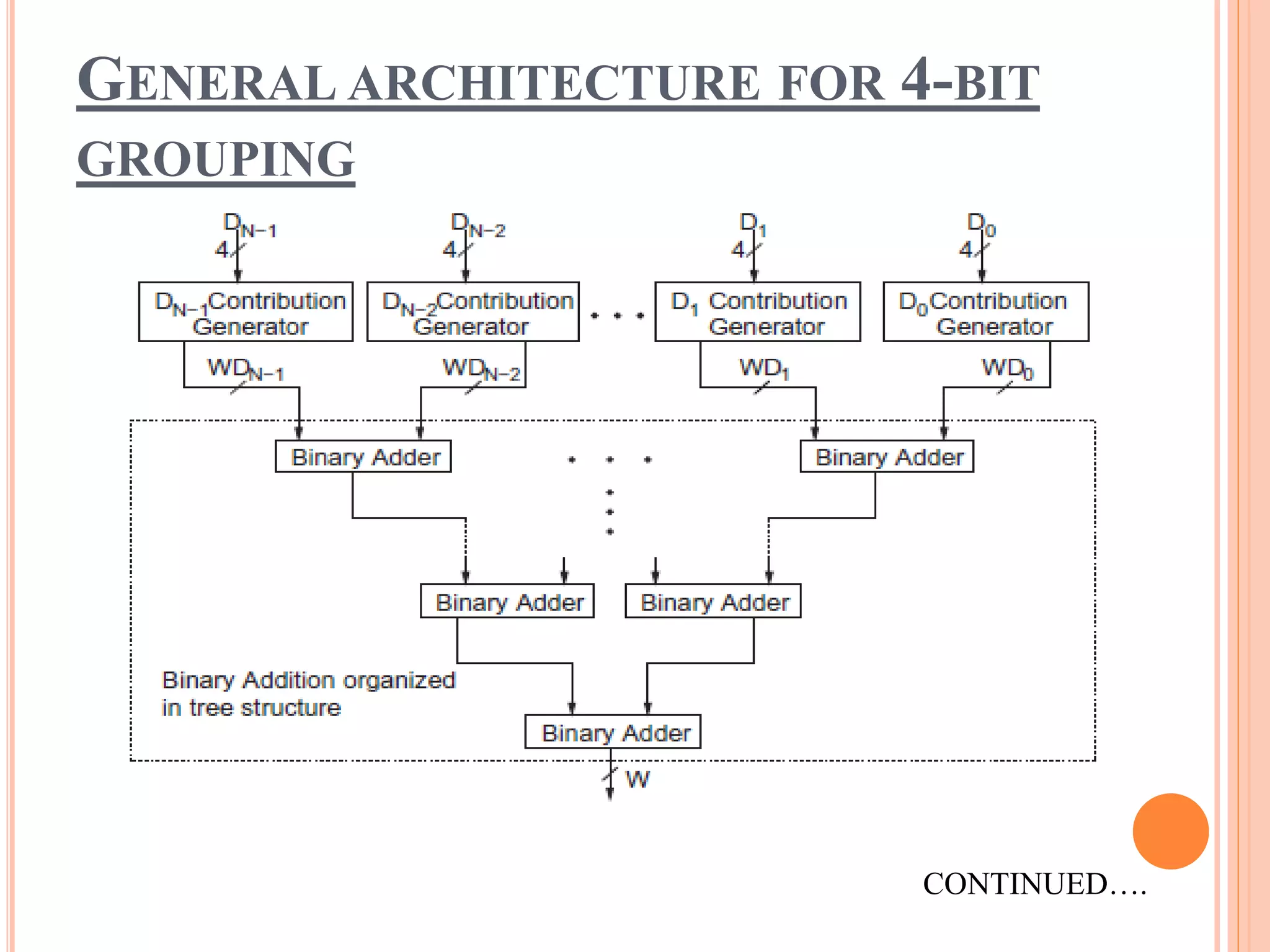
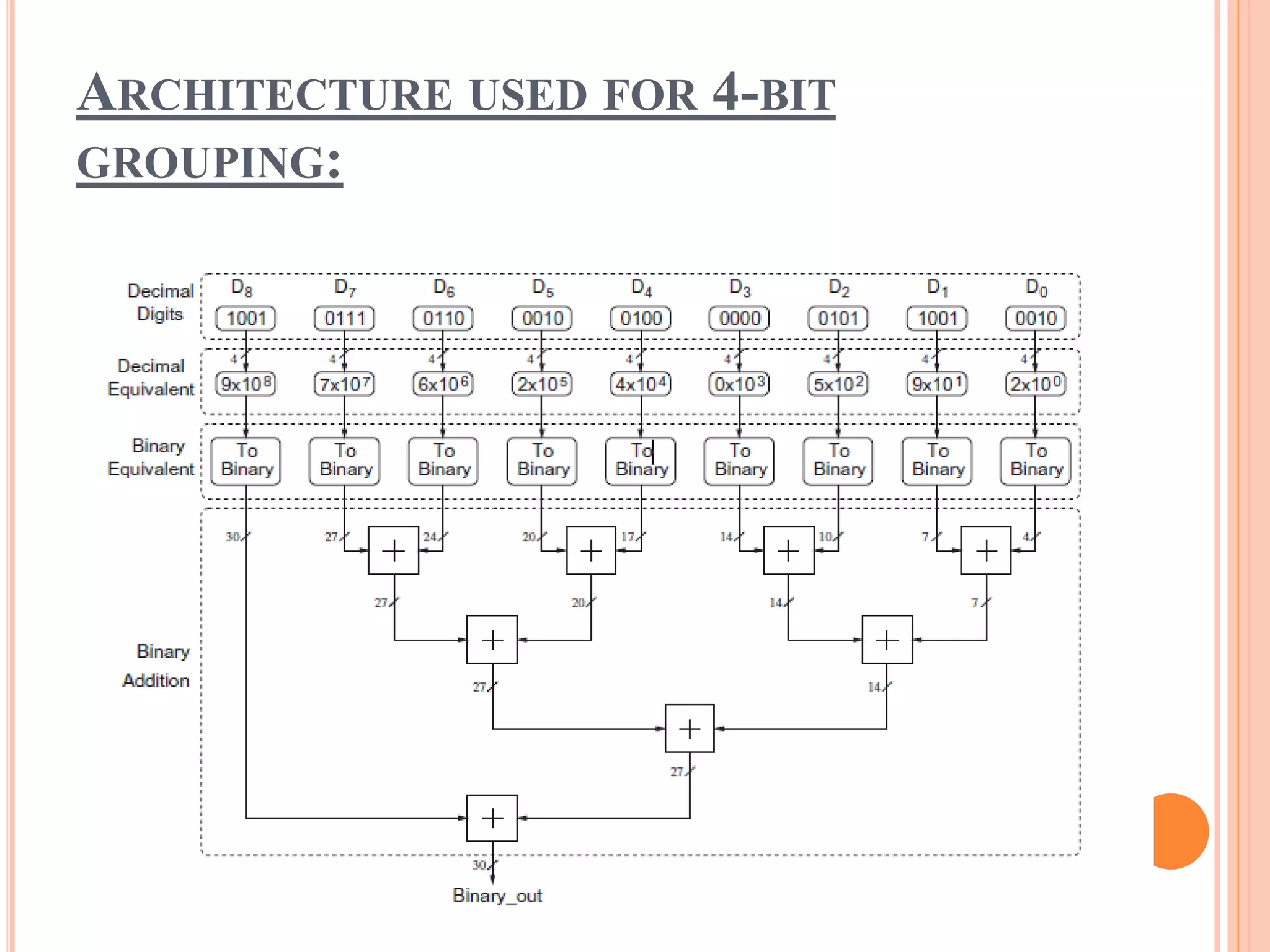
14. HOW TO CALCULATE SIZE OF WDI ?
Digit at position i contributes to the final binary result
with size WDi can be manually calculated as :
WDi = [log2 ( 9 x10i )]+ 1 bits; i = 0, 1, . . . N – 1,
and the final binary result w requires W bits where
W = [log2 (10N -1)]+ 1 bits.

15. 6 BIT GROUPING:
 In this grouping size of each group is 6 bits i.e. 1.5
BCD digits.
 The decimal equivalent of each group is formed
based on the 2 and 4 bits that compose the group

16. ARCHITECTURE USED FOR 6-BIT
GROUPING:

17. 8-BIT GROUPING:
 In this grouping, size of the group is 8 bits i.e. 2
BCD digits.
 The size of the most significant group in this
grouping can be 8 bits or 4 bits according to
number of BCD digits in the input.

18. ABOUT FPGA:
 FPGAs are programmable semiconductor devices that are based
around a matrix of Configurable Logic Blocks (CLBs) connected
through programmable interconnects.
 As opposed to Application Specific Integrated Circuits (ASICs),
where the device is custom built for the particular design, FPGAs
can be programmed to the desired application or functionality
requirements.
 Although One-Time Programmable (OTP) FPGAs are available, the
dominant type are SRAM-based which can be reprogrammed as the
design evolves.

19. FPGAARCHITECTURE:

20. FPGA IMPLEMENTATION:
 The implementation of our various bit-grouping schemes
varies from one FPGA family to another based on the
size of the look-up table (LUT) and the fabrication
technology of the FPGA family.
 Logic function of 4 variables fits into a single 4-input
LUT.
 6-variable function requires a hierarchy of 4-input LUTs
to be implemented on 4-input LUT FPGAs.

21. APPLICATIONS:
 Android apps.
 Scientific calculator.
 Desktop & laptops.
 Smart phones.

22. TOOL USED:
 Questa Sim 10.0b
 Xilinx 14.1

23. CONCLUSION
 We present high performance FPGA based decimal to
binary conversion scheme to support BCD arithmetic
based on binary hardware .
 The architecture presented here requires less LUTs as
compare to others and delay is also reduce by the help of
shifters in place of multipliers.

24. PROPOSED WORK
Hardware implementation of decimal to
binary conversion in FPGA.
 To reduce LUT’s(area) and delay.

25. REFERENCES
 M. Véstias, H. Neto, “Parallel decimal multipliers using
binary multipliers”, VI Southern Programmable Logic
Conference (SPL), 2010, pp. 73–78.
 H. Neto, M. Véstias, “Decimal multiplier on FPGA using
embedded binary multipliers”, International Conference on
Field Programmable Logic and Applications, 2008, FPL,
2008, pp. 197–202.
 M. Vestias, H. Neto, “ Iterative decimal multiplication using
binary arithmetic”, VII Southern Conference on
Programmable Logic (SPL), 2011, pp. 257–262.
 R.F. Tinder, “ Engineering Digital Design”, second ed.,
Elsevier, 2002.

26. ABOUT US
 Company Name: SiliconMentor
 Website: http://www.siliconmentor.com/
 For any enquiry feel free to contact us.