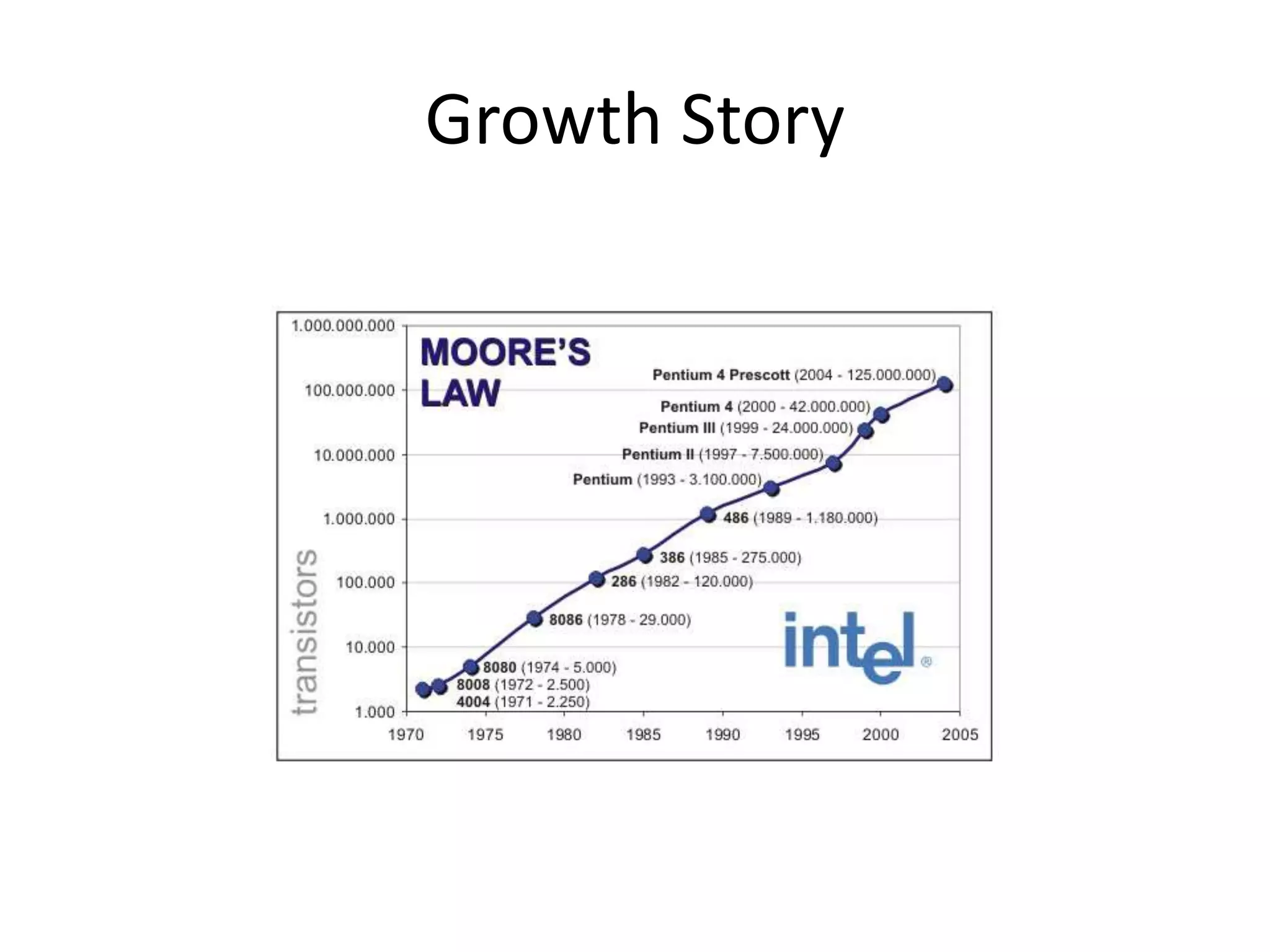
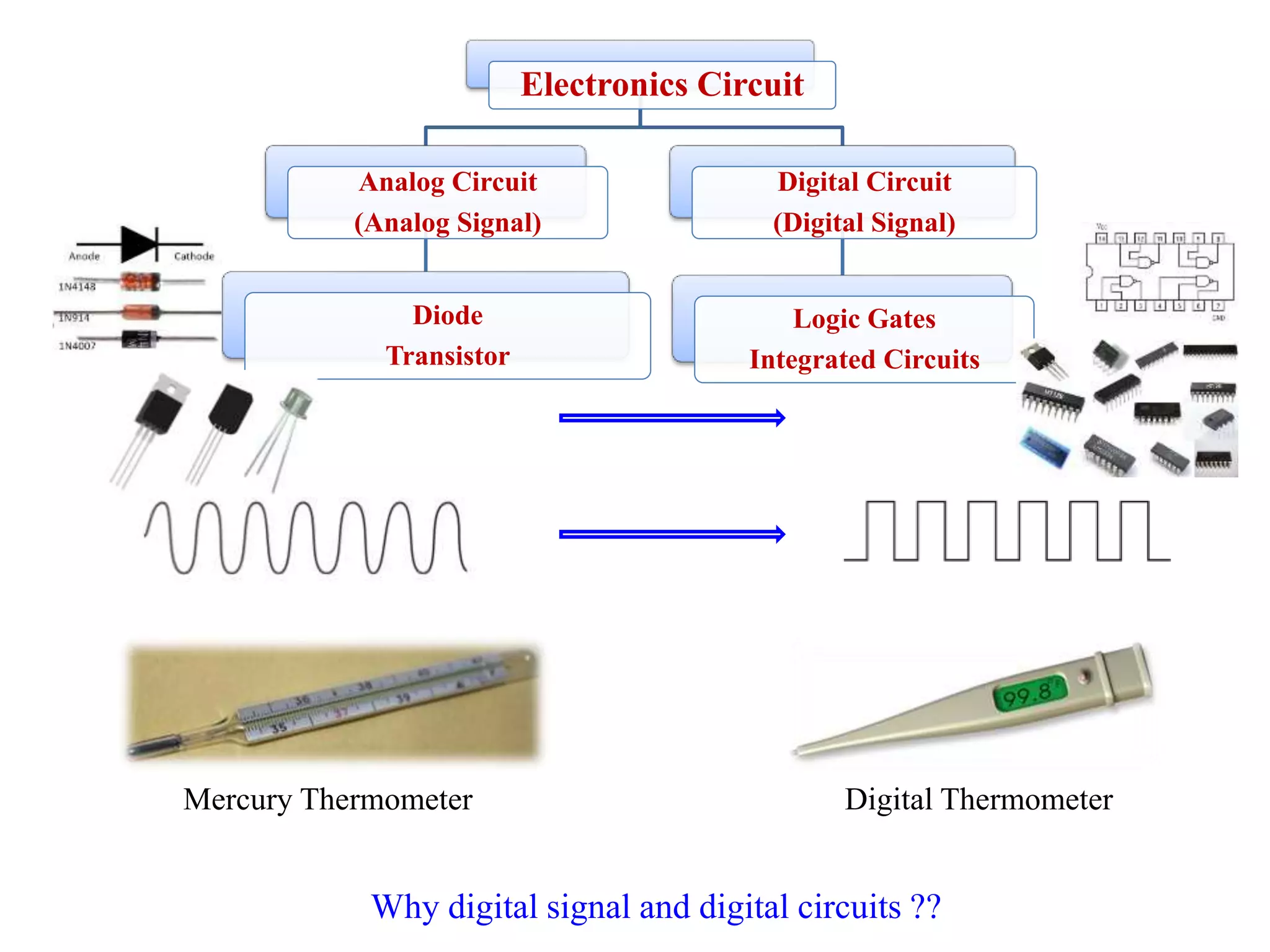
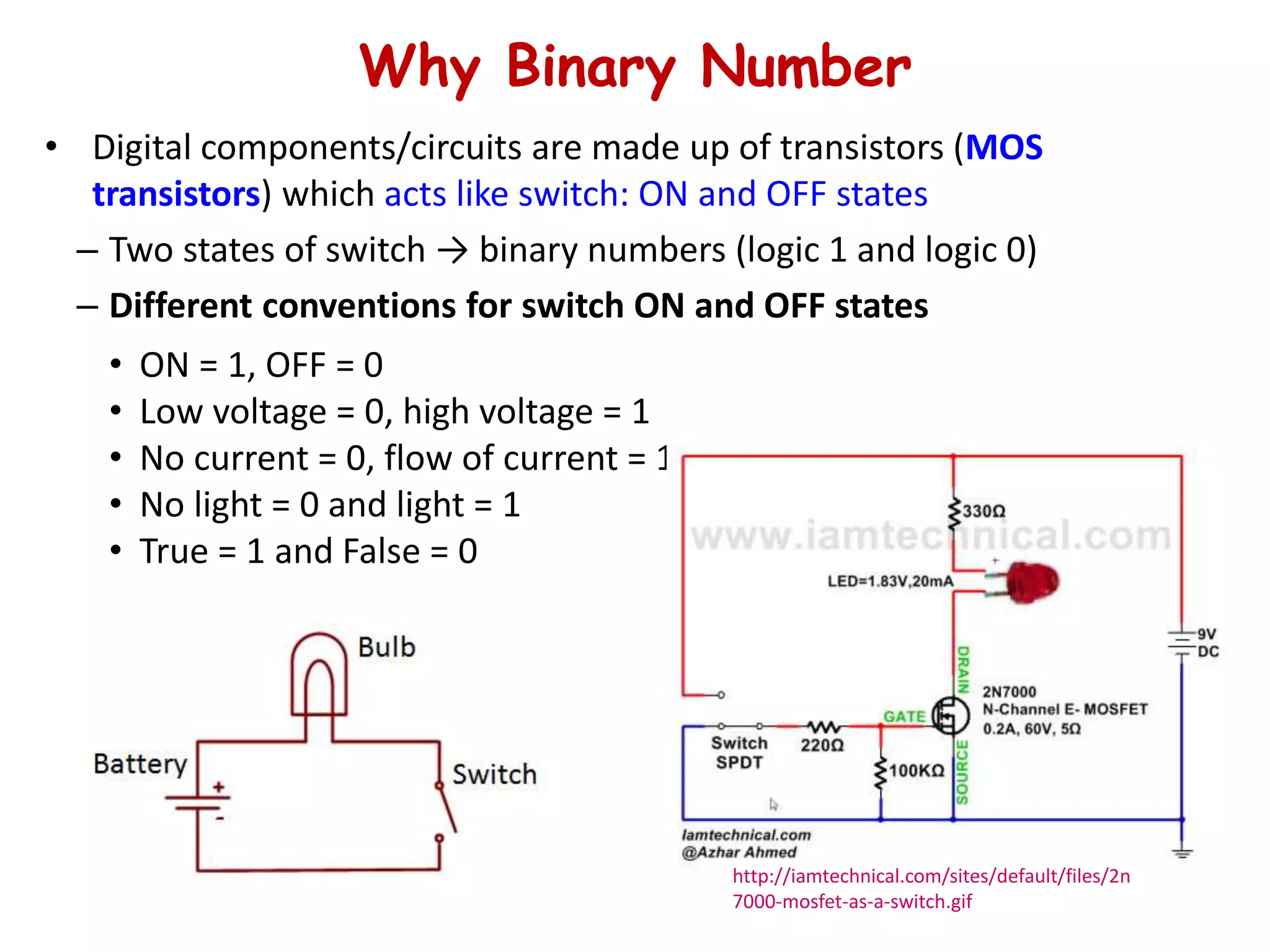
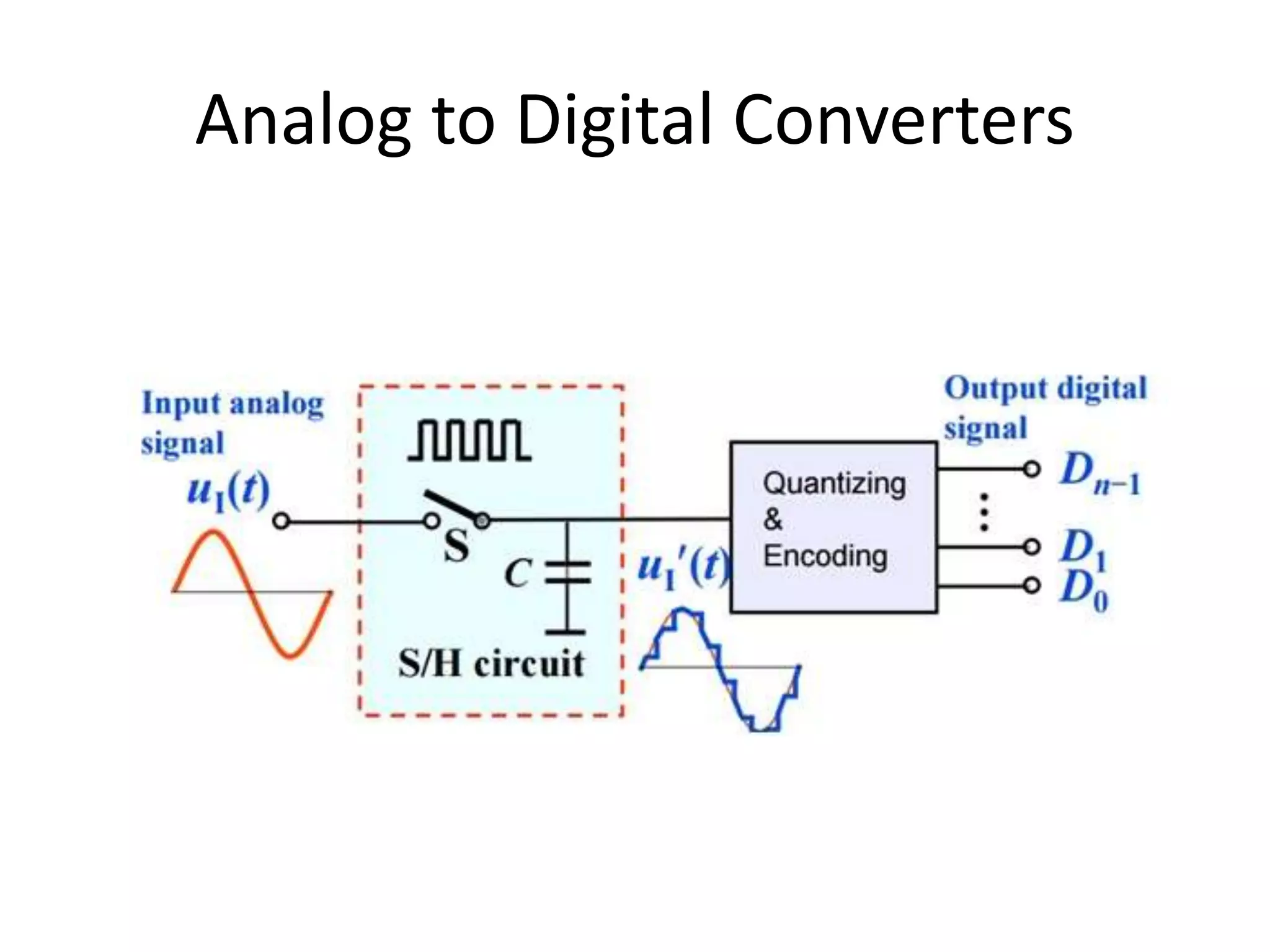
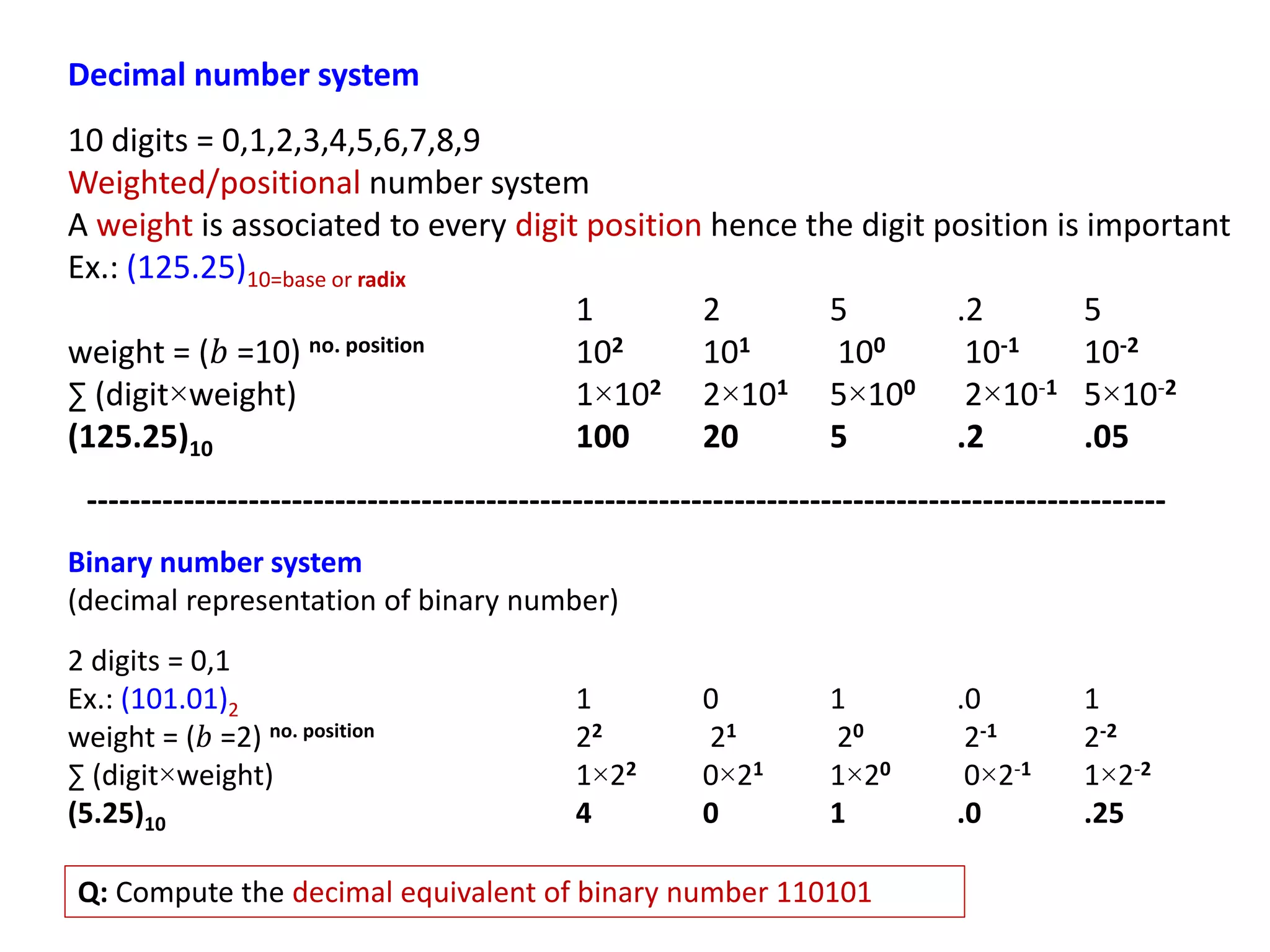
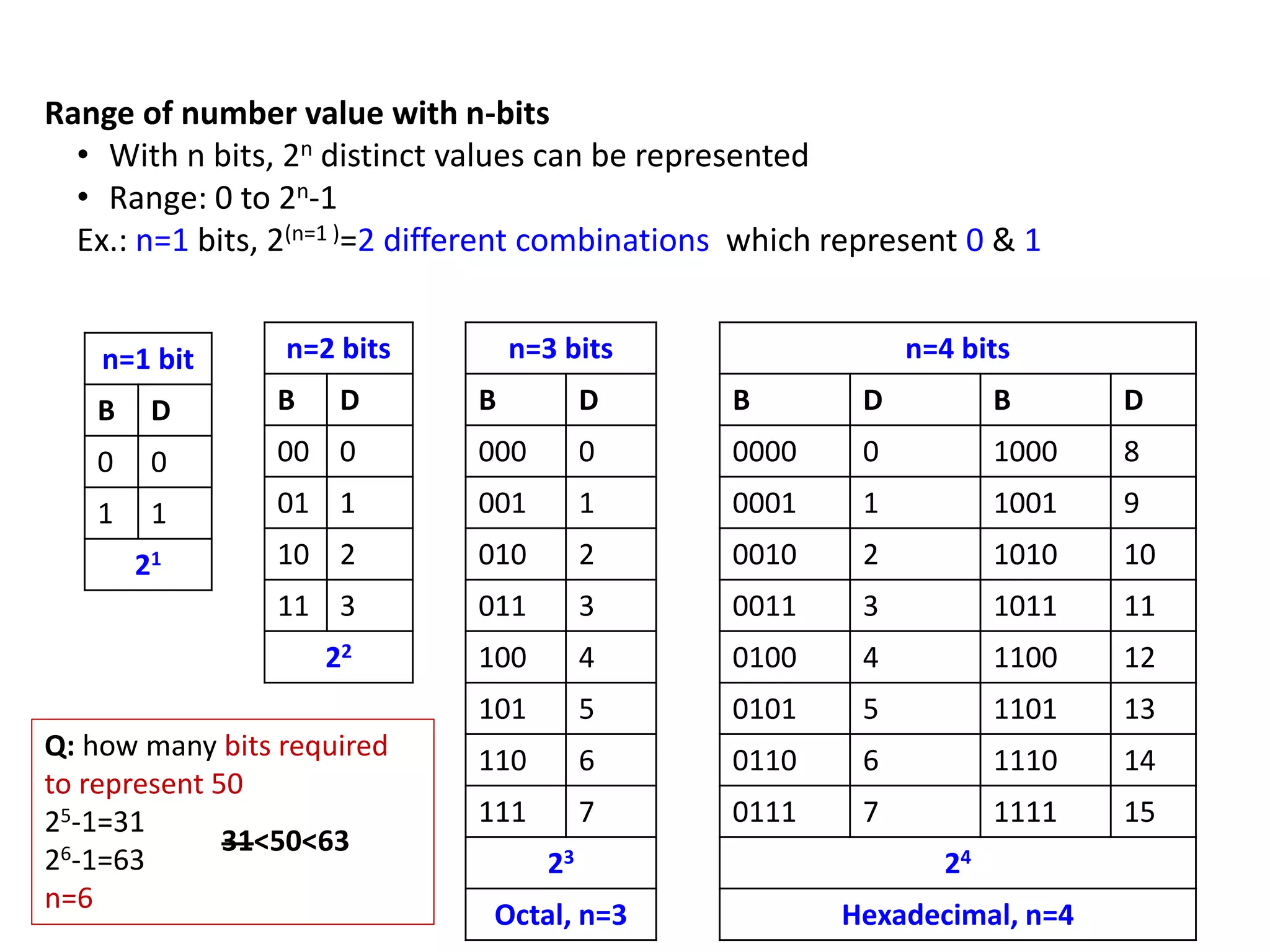
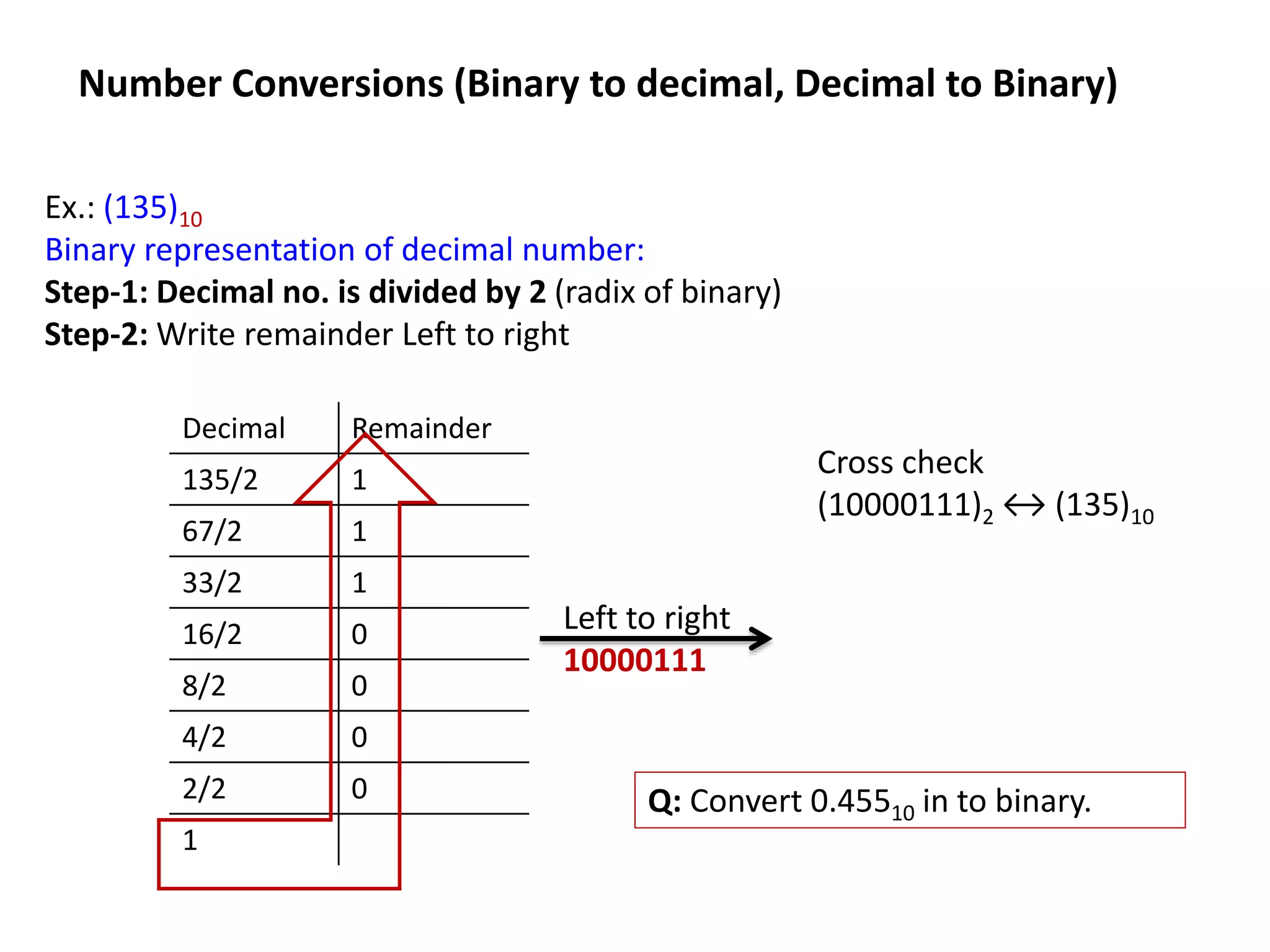
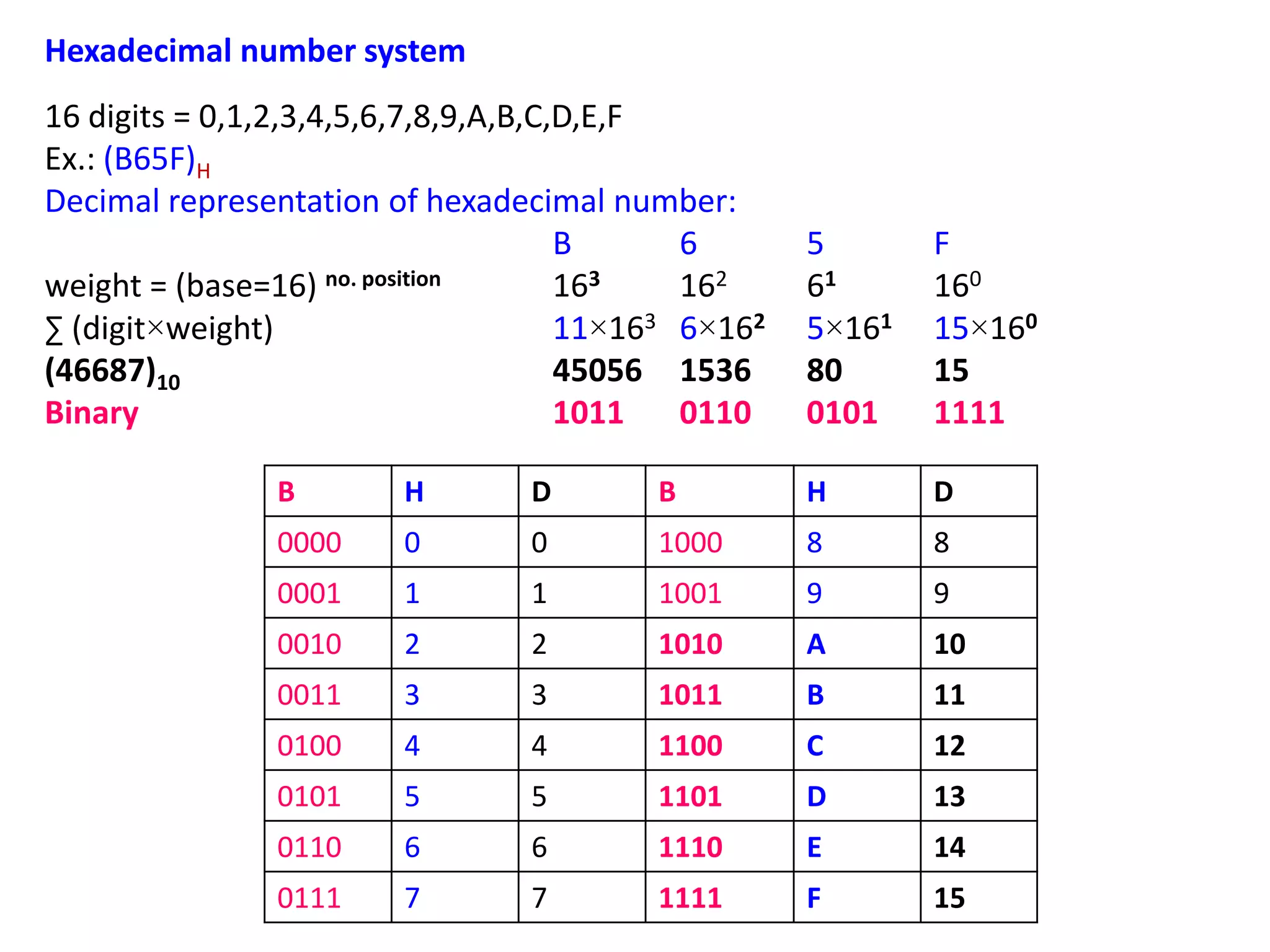
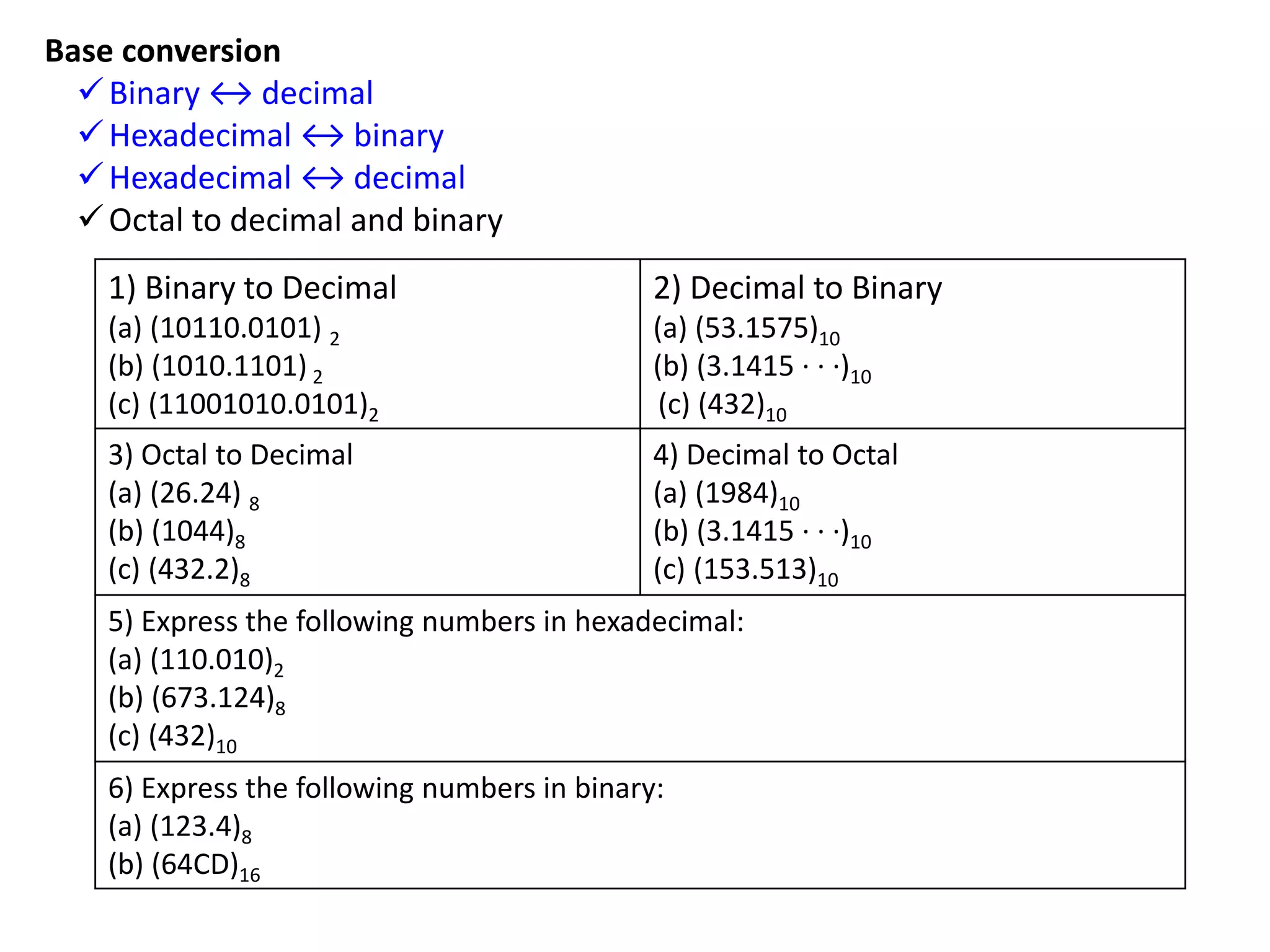
This document provides an overview of digital electronics, including: - A brief history of electronics from the invention of the light bulb to transistors. - An explanation of analog vs. digital signals and circuits, noting that digital circuits use discrete values represented by binary numbers. - How analog data is converted to digital data using analog-to-digital converters. - Different number systems used in digital electronics like binary, decimal, hexadecimal and their properties. 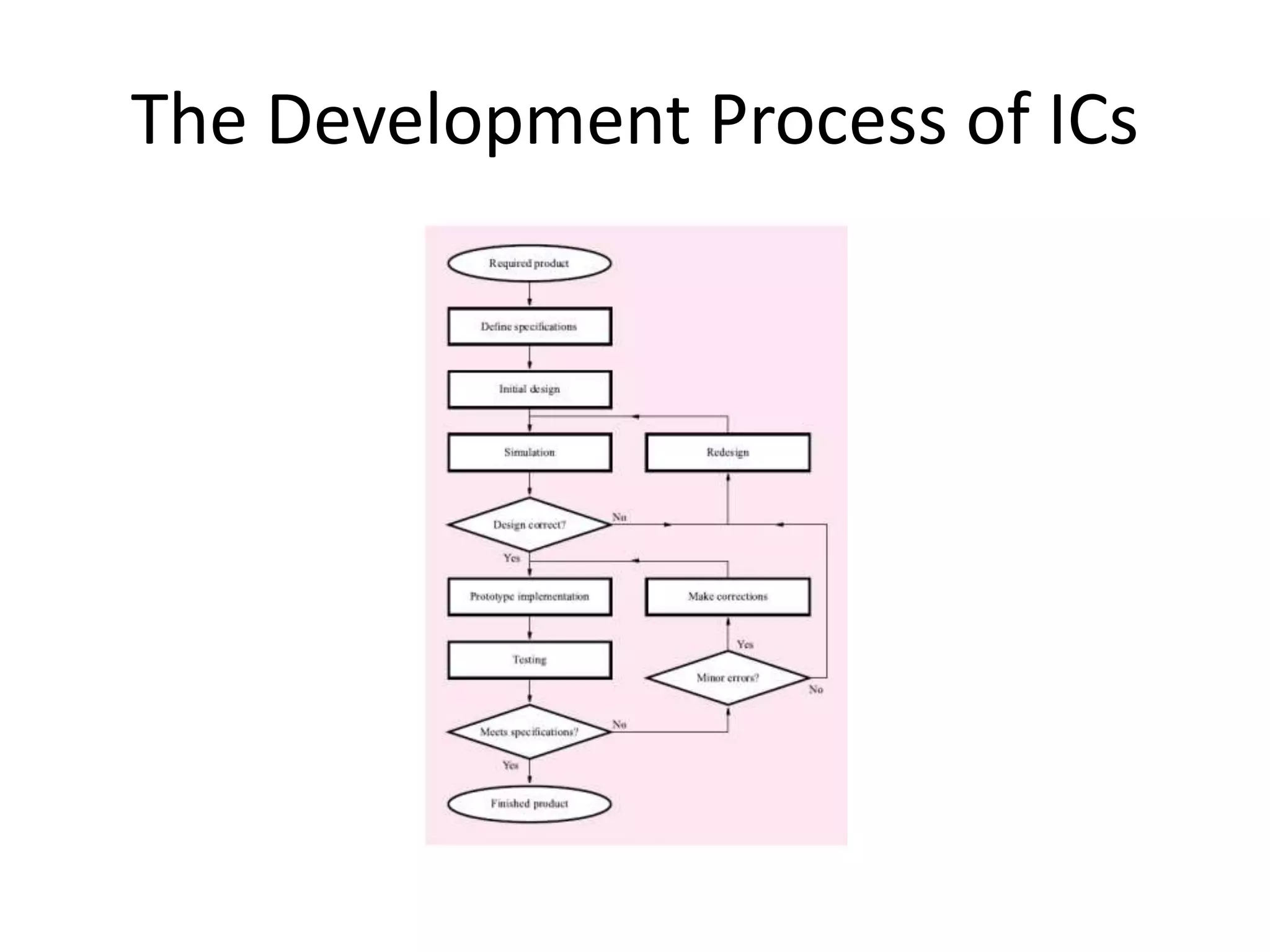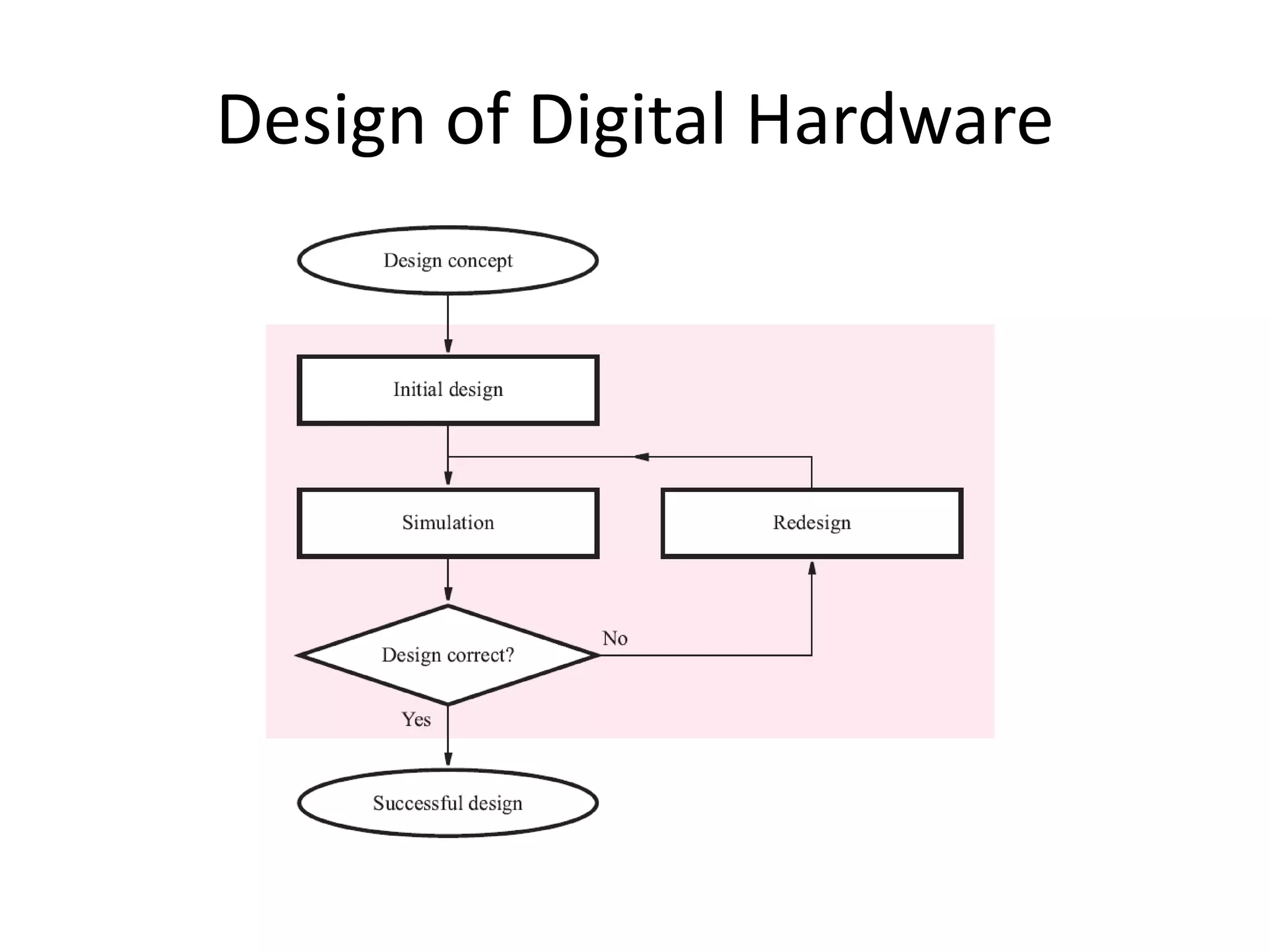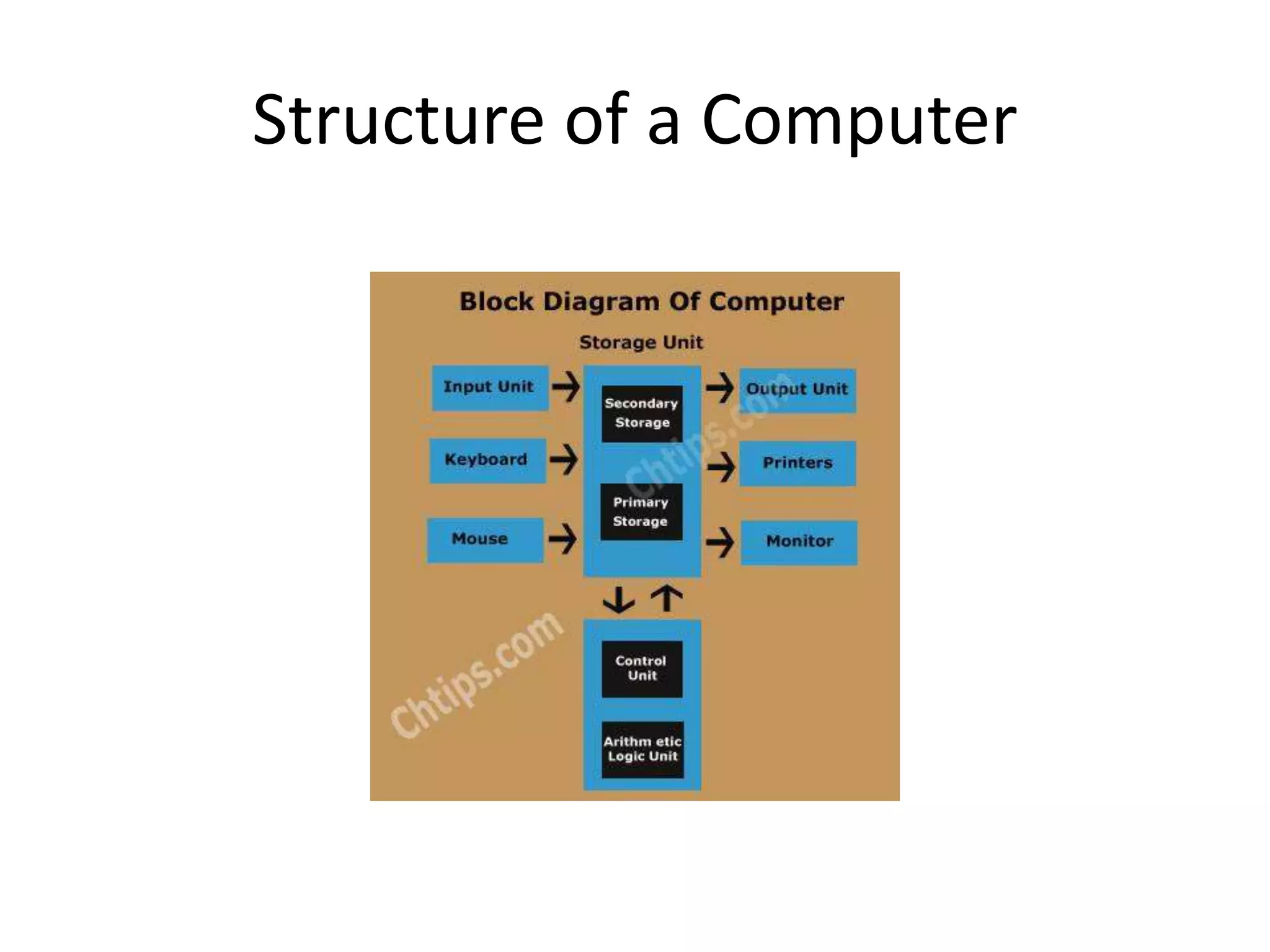- Examples of digital systems like computers, wireless communication, and how digital hardware is designed and implemented using programmable logic devices and application-specific integrated circuits.

1. Digital Electronics

2. Contents
• Background (History)
• Analog Vs Digital
• Conversion of Analog data to Digital data
• Binary System
• Number Systems

3. Brief History of Electronics
• 1878 Thomas Edison invented the Incandescent
light bulb.
• 1904 John Ambrose Fleming invented the diode
("oscillation valve“).
• 1907 Lee De Forest invented the triode tube.
• 1948 Bell lab developed Transistors. Scientists
names are Bardeen, Brattain, and Shockley
• Development of IC: 1958 Jack Kilby of Texas
Instruments and Robert Noyce of Fairchild
Semiconductor

5. Development of Semiconductors

6. Growth Story

7. The Development Process of ICs

8. Goal
1. Transforming Engineers to build capability of
designing and implementing complex digital
systems.
2. Use a hardware description Language (VHDL),
Verilog
3. Gain over all knowledge of digital system

9. Electronics Circuit
Analog Circuit
(Analog Signal)
Diode
Transistor
Digital Circuit
(Digital Signal)
Logic Gates
Integrated Circuits
Why digital signal and digital circuits ??
Mercury Thermometer Digital Thermometer

10. Recap:
 Applications of digital systems in society
 Difference between analog and digital signals/circuits
Analog signal have continuous
varying values
Digital signal have discrete set
of values
Information in the form of numbers, text, audio, and video
In digital system all the data is in the form of binary number
Q. Why digital?
 Digital data can be processed and transmitted more efficiently and
reliably
 Storage of digital data require less space and reproduced with great
accuracy
 Noise (unwanted voltage fluctuation) does not affect digital data
compared to analog data
Data ??

11. Digital Vs Analog
Accuracy
Programmability
Maintainability
Design Automation
 Area (cost), Power, performance, Bandwidth,
High frequency operation

12. Example of Digital Systems
• Computer
• Wireless communication system
• Digital TV
• Washing Machine
• Camera

13. Design of Digital Hardware

14. Structure of a Computer

15. Digital Hardware Products
For implementing circuits, three main types of chips
may be used:
1) Standard chips: Each standard chip contains a small amount of
circuitry (usually involving fewer than 100 transistors) and performs
a simple function.
2) Programmable logic devices: These chips have a very general
structure and include a collection of programmable switches that
allow the internal circuitry in the chip to be configured in many
different ways (PLDs, and FPGAs).
3) Custom chips: Such chips are intended for use in specific
applications and are sometimes called application-specific
integrated circuits (ASICs).

16. Analog to Digital Converters

17. Why Binary Number
• Digital components/circuits are made up of transistors (MOS
transistors) which acts like switch: ON and OFF states
– Two states of switch → binary numbers (logic 1 and logic 0)
– Different conventions for switch ON and OFF states
• ON = 1, OFF = 0
• Low voltage = 0, high voltage = 1
• No current = 0, flow of current = 1
• No light = 0 and light = 1
• True = 1 and False = 0
http://iamtechnical.com/sites/default/files/2n
7000-mosfet-as-a-switch.gif

18. Example: Digital Computer which receives data (input data), stores and
processes it, and produces data (output data)
Data: numbers, text, audio, and video in the form of binary numbers (string
of 0s and 1s), 2 digits = 0, 1. Ex.: 1001
Bit single binary digit (0 or 1)
Nibble collection of 4 bits
Byte collection of 8 bits
Word collection of 16/32/64 bits
1 Kbyte 2^10 bytes = 1024 bytes
1 Mbyte 2^20 bytes
1 Gbyte 2^30 bytes

19. Number System
Two categories: Weighted and non-weighted
Weighted/positional number system ??
A weight is associated to every digit position hence the digit position is
important
Ex.: Decimal number 125.25
Most used number systems:
 Decimal (10 digits: 0,1,2,3,4,5,6,7,8,9)
 Binary (2 digits: 0, 1)
 Octal (8 digits: 0,1,2,3,4,5,6,7)
 Hexadecimal (16 digits: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F)

20. Generalized Number
In General a number represented as:
• N 𝑏 = d𝑛−1d𝑛−2 … d1d0 . d−1d−2 …
• Number 𝑏𝑎𝑠𝑒/𝑟𝑎𝑑𝑖𝑥 =
𝐼𝑛𝑡𝑒𝑔𝑟𝑎𝑙 𝑝𝑜𝑟𝑡𝑖𝑜𝑛 𝑅𝑎𝑑𝑖𝑥 𝑝𝑜𝑖𝑛𝑡 𝐹𝑟𝑎𝑐𝑡𝑖𝑜𝑛𝑎𝑙 𝑝𝑜𝑖𝑛𝑡
 N 𝑏 = d𝑛−1𝑏𝑛−1
+ d𝑛−2𝑏𝑛−2
+ ⋯ + d1𝑏1
+

21. Decimal number system
10 digits = 0,1,2,3,4,5,6,7,8,9
Weighted/positional number system
A weight is associated to every digit position hence the digit position is important
Ex.: (125.25)10=base or radix
1 2 5 .2 5
weight = (𝑏 =10) no. position 102 101 100 10-1 10-2
∑ (digit×weight) 1×102 2×101 5×100 2×10-1 5×10-2
(125.25)10 100 20 5 .2 .05
----------------------------------------------------------------------------------------------------
Binary number system
(decimal representation of binary number)
2 digits = 0,1
Ex.: (101.01)2 1 0 1 .0 1
weight = (𝑏 =2) no. position 22 21 20 2-1 2-2
∑ (digit×weight) 1×22 0×21 1×20 0×2-1 1×2-2
(5.25)10 4 0 1 .0 .25
Q: Compute the decimal equivalent of binary number 110101

22. Range of number value with n-bits
• With n bits, 2n distinct values can be represented
• Range: 0 to 2n-1
Ex.: n=1 bits, 2(n=1 )=2 different combinations which represent 0 & 1
n=2 bits
B D
00 0
01 1
10 2
11 3
22
n=3 bits
B D
000 0
001 1
010 2
011 3
100 4
101 5
110 6
111 7
23
Octal, n=3
n=4 bits
B D B D
0000 0 1000 8
0001 1 1001 9
0010 2 1010 10
0011 3 1011 11
0100 4 1100 12
0101 5 1101 13
0110 6 1110 14
0111 7 1111 15
24
Hexadecimal, n=4
n=1 bit
B D
0 0
1 1
21
Q: how many bits required
to represent 50
25-1=31
26-1=63
n=6
31<50<63

23. Ex.: (135)10
Binary representation of decimal number:
Step-1: Decimal no. is divided by 2 (radix of binary)
Step-2: Write remainder Left to right
Decimal Remainder
135/2 1
67/2 1
33/2 1
16/2 0
8/2 0
4/2 0
2/2 0
1
Cross check
(10000111)2 ↔ (135)10
Left to right
10000111
Q: Convert 0.45510 in to binary.
Number Conversions (Binary to decimal, Decimal to Binary)

24. Conversion of Fraction

25. Hexadecimal number system
16 digits = 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
Ex.: (B65F)H
Decimal representation of hexadecimal number:
B 6 5 F
weight = (base=16) no. position 163 162 61 160
∑ (digit×weight) 11×163 6×162 5×161 15×160
(46687)10 45056 1536 80 15
Binary 1011 0110 0101 1111
B H D B H D
0000 0 0 1000 8 8
0001 1 1 1001 9 9
0010 2 2 1010 A 10
0011 3 3 1011 B 11
0100 4 4 1100 C 12
0101 5 5 1101 D 13
0110 6 6 1110 E 14
0111 7 7 1111 F 15

26. Base conversion
Binary ↔ decimal
Hexadecimal ↔ binary
Hexadecimal ↔ decimal
Octal to decimal and binary
1) Binary to Decimal
(a) (10110.0101) 2
(b) (1010.1101) 2
(c) (11001010.0101)2
2) Decimal to Binary
(a) (53.1575)10
(b) (3.1415 · · ·)10
(c) (432)10
3) Octal to Decimal
(a) (26.24) 8
(b) (1044)8
(c) (432.2)8
4) Decimal to Octal
(a) (1984)10
(b) (3.1415 · · ·)10
(c) (153.513)10
5) Express the following numbers in hexadecimal:
(a) (110.010)2
(b) (673.124)8
(c) (432)10
6) Express the following numbers in binary:
(a) (123.4)8
(b) (64CD)16

27. Tips for Big number conversion
Binary ↔ Decimal
• Example: 675.625 10 = ? 2
Decimal Remainder
675/16 3
42/16 A
2
Decimal Integer
0.625×16 A
0

28. Suggested Readings
 M. M. Mano, Digital Design, PHI
 S. Brown and Z. Vranesis, Fundamental of Digital Logic with VHDL design,
Tata Mc GRAW-Hill , 2003
 J. F. Wakerly, Digital Design Principles and Practices, Prentice-Hall , 2005