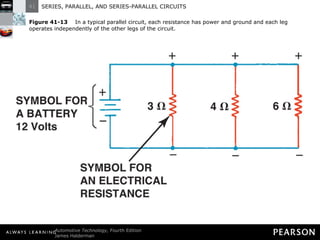
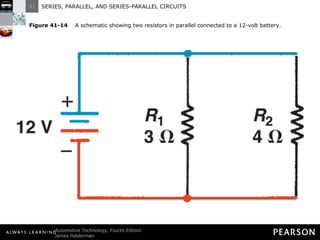
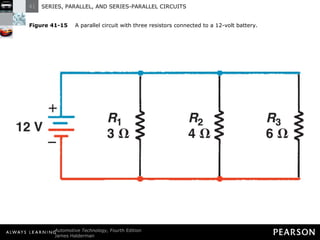
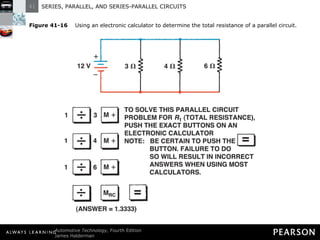
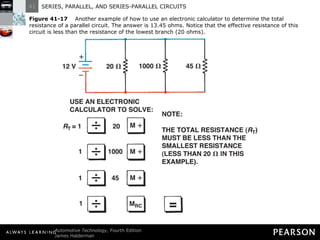
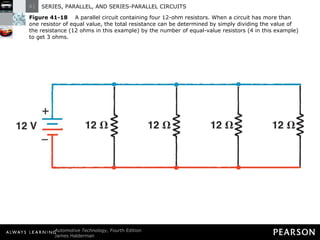
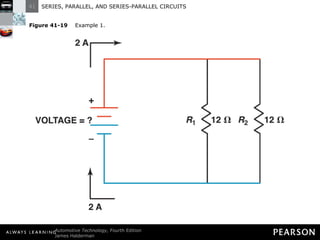
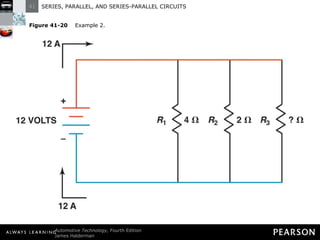
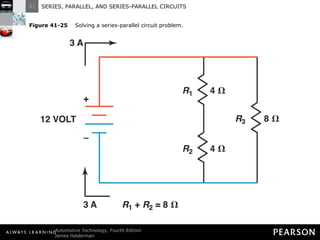
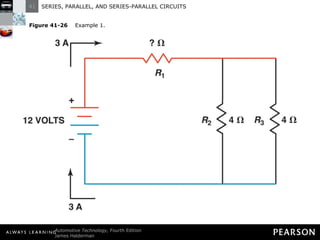
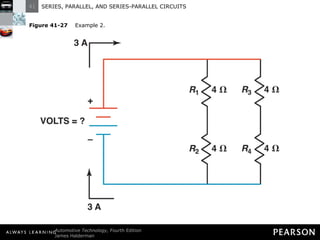
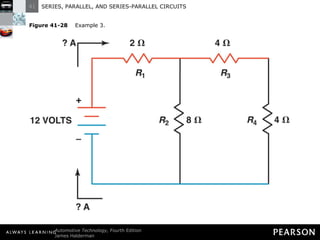
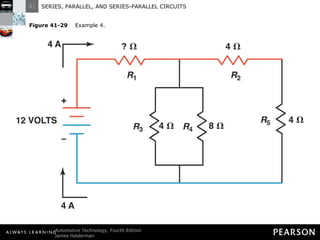
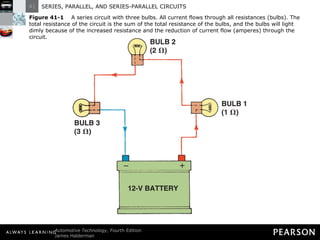
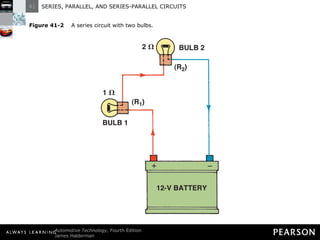
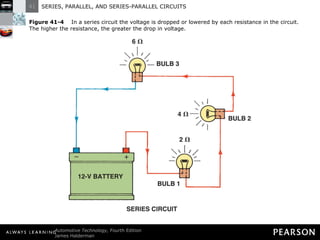
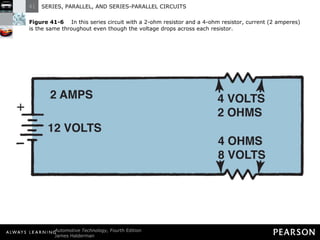
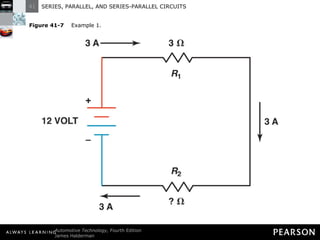
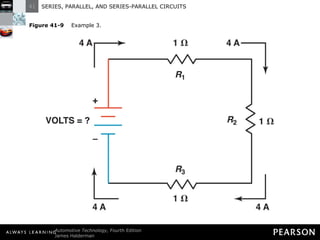
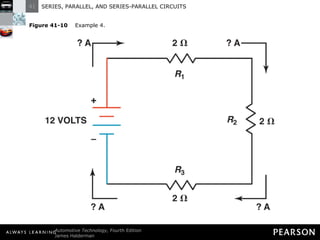
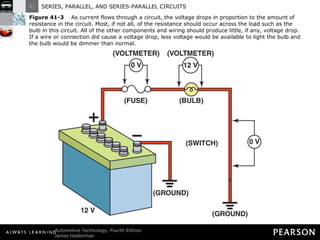
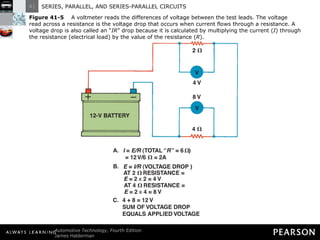
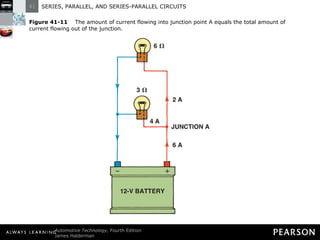
This document discusses series, parallel, and series-parallel circuits. It begins by defining the objectives and characteristics of each type of circuit. Key points include: - In a series circuit, current flows through all components in a single path and total resistance equals the sum of individual resistances. - Kirchhoff's laws state that the total voltage around any closed circuit equals the sum of the voltage drops, and the current entering a junction equals the current leaving. 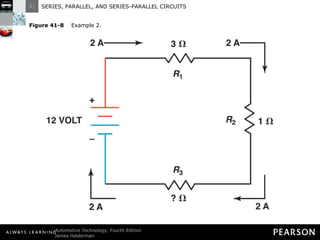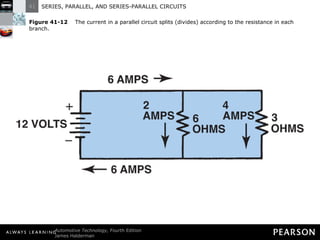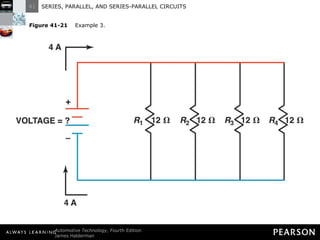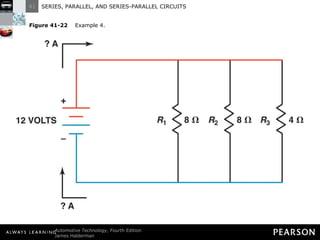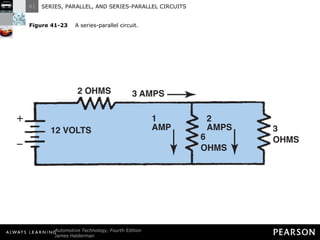- Parallel circuits have multiple current paths and the same voltage across each branch, while current varies depending on resistance. Total resistance is less than the smallest individual resistance.

1. SERIES, PARALLEL, AND SERIES-PARALLEL CIRCUITS 41

2. Objectives The student should be able to: Prepare for ASE Electrical/Electronic Systems (A6) certification test content area “A” (General Electrical/Electronic System Diagnosis). Identify a series circuit. Identify a parallel circuit. Identify a series-parallel circuit. Calculate the total resistance in a parallel circuit.

3. Objectives The student should be able to: State Kirchhoff’s voltage law. Calculate voltage drops in a series circuit. Explain series and parallel circuit laws. State Kirchhoff’s current law. Identify where faults in a series-parallel circuit can be detected or determined.

4. SERIES CIRCUITS

5. Series Circuits Complete circuit with more than one load Current has only one path to flow through all loads

6. OHM’S LAW AND SERIES CIRCUITS

7. Ohm’s Law and Series Circuits Total resistance is sum of all resistances in circuit Formula for total resistance ( R T ) R T = R 1 + R 2 + R 3 + . . .

8. Figure 41-1 A series circuit with three bulbs. All current flows through all resistances (bulbs). The total resistance of the circuit is the sum of the total resistance of the bulbs, and the bulbs will light dimly because of the increased resistance and the reduction of current flow (amperes) through the circuit.

9. Ohm’s Law and Series Circuits Total resistance of circuit shown is 6 ohms (1 Ω + 2 Ω +3 Ω) Use Ohm’s law to find current flow: I = E / R = 12 V/6 Ω = 2 A With total resistance of 6 ohms using a 12-volt battery in series circuit shown, 2 amperes current flow through entire circuit

10. Figure 41-2 A series circuit with two bulbs.

11. Ohm’s Law and Series Circuits One resistance eliminated Total resistance now 3 ohms (1 Ω + 2 Ω) Current flow now 4 amperes: I = E / R = 12 V/3 Ω = 4 A Current flow doubled (4 A instead of 2 A) when resistance cut in half

12. KIRCHHOFF’S VOLTAGE LAW

13. Kirchhoff’s Voltage Law Kirchhoff’s Second Law: Voltage around any closed circuit is equal to the sum (total) of the voltage drops across the resistances Voltage applied through a series circuit drops with each resistor

14. Kirchhoff’s Voltage Law Similar to how strength of athlete drops after each strenuous physical feat The greater the resistance, the greater the drop in voltage

15. Figure 41-3 As current flows through a circuit, the voltage drops in proportion to the amount of resistance in the circuit. Most, if not all, of the resistance should occur across the load such as the bulb in this circuit. All of the other components and wiring should produce little, if any, voltage drop. If a wire or connection did cause a voltage drop, less voltage would be available to light the bulb and the bulb would be dimmer than normal.

16. Figure 41-4 In a series circuit the voltage is dropped or lowered by each resistance in the circuit. The higher the resistance, the greater the drop in voltage.

17. Kirchhoff’s Voltage Law Applying Kirchhoff’s Voltage Law Total resistance of circuit determined by adding individual resistances (2 Ω + 4 Ω + 6 Ω = 12 Ω)

18. Kirchhoff’s Voltage Law Applying Kirchhoff’s Voltage Law Current through circuit determined using Ohm’s law I = E / R = 12 V/12 Ω = 1 A

19. Kirchhoff’s Voltage Law Applying Kirchhoff’s Voltage Law In circuit shown, following values are known: Resistance = 12 Ω, Voltage = 12 V, Current = 1 A

20. Kirchhoff’s Voltage Law Applying Kirchhoff’s Voltage Law Voltage drop determined using Ohm’s law and calculating for voltage ( E ) using value of each resistance individually: E = I × R Voltage drop for bulb 1: E = I × R = 1 A × 2 Ω = 2 V

21. Kirchhoff’s Voltage Law Applying Kirchhoff’s Voltage Law Voltage drop determined using Ohm’s law and calculating for voltage ( E ) using value of each resistance individually: E = I × R Voltage drop for bulb 2: E = I × R = 1 A × 4 Ω = 4 V

22. Kirchhoff’s Voltage Law Applying Kirchhoff’s Voltage Law Voltage drop determined using Ohm’s law and calculating for voltage ( E ) using value of each resistance individually: E = I × R Voltage drop for bulb 3: E = I × R = 1 A × 6 Ω = 6 V

23. Kirchhoff’s Voltage Law Applying Kirchhoff’s Voltage Law Sum of voltage drops should equal applied voltage (battery voltage): Total of voltage drops = 2 V + 4 V + 6 V = 12 V = Battery voltage

24. Kirchhoff’s Voltage Law Applying Kirchhoff’s Voltage Law This illustrates Kirchhoff’s second (voltage) law Another example is illustrated in FIGURE 41–5

25. Figure 41-5 A voltmeter reads the differences of voltage between the test leads. The voltage read across a resistance is the voltage drop that occurs when current flows through a resistance. A voltage drop is also called an “ IR ” drop because it is calculated by multiplying the current ( I ) through the resistance (electrical load) by the value of the resistance ( R ).

26. Kirchhoff’s Voltage Law Use of Voltage Drops Used in automotive electrical systems to drop voltage in: Dash lights High voltage to bulbs makes them bright; low voltage results in dim light

27. Kirchhoff’s Voltage Law Use of Voltage Drops Used in automotive electrical systems to drop voltage in: Blower motor (heater or air-conditioning fan) Highest resistance drops voltage most, causing lowest speed

28. Kirchhoff’s Voltage Law Use of Voltage Drops Used in automotive electrical systems to drop voltage in: Blower motor (heater or air-conditioning fan) Highest speed occurs when no resistance in circuit ?

29. SERIES CIRCUIT LAWS

30. Series Circuit Laws LAW 1: Total resistance in series circuit is sum total of individual resistances. Resistance values of each electrical load are simply added together. LAW 2: Current is constant throughout entire circuit. If 2 amperes of current leave battery, 2 amperes of current return to battery.

31. Figure 41-6 In this series circuit with a 2-ohm resistor and a 4-ohm resistor, current (2 amperes) is the same throughout even though the voltage drops across each resistor.

32. Series Circuit Laws LAW 3: Although current (in amperes) is constant, voltage drops across each resistance in circuit. Voltage drop across each load is proportional to value of resistance compared to total resistance. If a resistance is one-half of total resistance: Voltage drop across that resistance one-half of applied voltage

33. Series Circuit Laws LAW 3: Although current (in amperes) is constant, voltage drops across each resistance in circuit. Voltage drop across each load is proportional to value of resistance compared to total resistance. If a resistance is one-half of total resistance: Sum total of all voltage drops equals applied source voltage

34. SERIES CIRCUIT EXAMPLES

35. Series Circuit Examples Each of four examples includes solving for: Total resistance in the circuit Current flow (amperes) through the circuit Voltage drop across each resistance

36. Figure 41-7 Example 1.

37. Series Circuit Examples Unknown is value of R 2 Total resistance calculated using Ohm’s law R Total = E / I = 12 volts/3 A = 4 Ω

38. Figure 41-8 Example 2.

39. Series Circuit Examples Because R 1 = 3 ohms and total resistance = 4 ohms, value of R 2 = 1 ohm Unknown is value of R 3 Total resistance calculated using Ohm’s law R Total = E / I = 12 volts/2 A = 6 Ω

40. Series Circuit Examples Total resistance of R 1 (3 ohms) + R 2 (1 ohm) = 4 ohms Value of R 3 difference between total resistance (6 ohms) and value of known resistance (4 ohms) 6 – 4 = 2 ohms = R 3

41. Figure 41-9 Example 3.

42. Series Circuit Examples Unknown value is voltage of battery Use Ohm’s law to solve for voltage ( E = I × R ) R in this problem refers to total resistance ( R T )

43. Series Circuit Examples Total resistance of series circuit determined by adding values of individual resistors R T = 1 Ω + 1 Ω + 1 Ω R T = 3 Ω

44. Series Circuit Examples Placing value for total resistance (3 Ω) into equation: battery voltage = 12 volts E = 4 A × 3 Ω E = 12 volts

45. Figure 41-10 Example 4.

46. Series Circuit Examples Unknown is current (amperes) in circuit Use Ohm’s law to solve for current I = E / R = 12 volts/6 ohms = 2 A

47. Series Circuit Examples Example uses total resistance in circuit (6 ohms) = total of 3 individual resistors (2 Ω + 2 Ω + 2 Ω = 6 Ω) Current through circuit = 2 amperes

48. PARALLEL CIRCUITS

49. Parallel Circuits Complete circuit with more than one path for current Separate paths which split and meet at junction points called branches, legs, shunts

50. Parallel Circuits Current flow through each branch varies depending on resistance in branch Break or open in one leg does not stop current flow through remaining legs

51. KIRCHHOFF’S CURRENT LAW

52. Kirchhoff’s Current Law First law: Current flowing into any junction of circuit equal to current flowing out of junction Can be illustrated using Ohm’s law

53. Figure 41-11 The amount of current flowing into junction point A equals the total amount of current flowing out of the junction.

54. Kirchhoff’s Current Law Kirchhoff’s law: amount of current flowing into junction A equals current flowing out of junction A

55. Kirchhoff’s Current Law Because 6-ohm leg requires 2 amperes and 3-ohm leg requires 4 amperes, wire from battery to junction A must be able to handle 6 amperes

56. Kirchhoff’s Current Law Sum of current flowing out of junction (2 + 4 = 6 A) equal to current flowing into junction (6 A), proving Kirchhoff’s current law

57. PARALLEL CIRCUIT LAWS

58. Parallel Circuit Laws LAW 1: Total resistance of parallel circuit always less than that of smallest-resistance leg. Occurs because not all current flows through each leg or branch With many branches, more current can flow from battery Similar to more vehicles traveling on five-lane road than one-lane road

59. Parallel Circuit Laws LAW 2: Voltage is same for each leg of parallel circuit

60. Parallel Circuit Laws LAW 3: Sum of individual currents in each leg equals total current. Amount of current flow may vary for each leg depending on leg’s resistance Current flowing through each leg results in same voltage drop (from power side to the ground side) as for every other leg of circuit

61. Figure 41-12 The current in a parallel circuit splits (divides) according to the resistance in each branch.

62. DETERMINING TOTAL RESISTANCE IN A PARALLEL CIRCUIT

63. Determining Total Resistance in a Parallel Circuit Five methods commonly used to determine total resistance in parallel circuit METHOD 1: Total current (in amperes) can be calculated first by treating each leg as simple circuit

64. Figure 41-13 In a typical parallel circuit, each resistance has power and ground and each leg operates independently of the other legs of the circuit.

65. Determining Total Resistance in a Parallel Circuit Each leg has its own power and ground (–) Current through each leg independent of current through other leg Current through 3-Ω resistance = I = E/R = 12 V/3 Ω = 4 A

66. Determining Total Resistance in a Parallel Circuit Current through each leg independent of current through other leg Current through 4-Ω resistance = I = E / R = 12 V/4 Ω = 3 A

67. Determining Total Resistance in a Parallel Circuit Current through each leg independent of current through other leg Current through 6-Ω resistance = I = E / R = 12 V/6 Ω = 2 A

68. Determining Total Resistance in a Parallel Circuit Total current flowing from battery sum total of individual currents for each leg Total current 9 amperes (4 A + 3 A + 2 A + 9 A)

69. Determining Total Resistance in a Parallel Circuit If total circuit resistance ( R T ) needed, Ohm’s law can calculate it because voltage ( E ) and current ( I ) now known R T = E / I = 12 V/9 A = 1.33 Ω

70. Determining Total Resistance in a Parallel Circuit If total circuit resistance ( R T ) needed, Ohm’s law can calculate it because voltage ( E ) and current ( I ) now known Total resistance (1.33 Ω) smaller than that of smallest-resistance leg of circuit Not all current flows through all resistances as in a series circuit

71. Determining Total Resistance in a Parallel Circuit Because current has alternative paths through legs of parallel circuit, as additional resistances (legs) added, total current from battery increases

72. Determining Total Resistance in a Parallel Circuit METHOD 2: If only two resistors connected in parallel, total resistance ( R T ) can be found R T = ( R 1 × R 2 )/( R 1 + R 2 )

73. Figure 41-14 A schematic showing two resistors in parallel connected to a 12-volt battery.

74. Determining Total Resistance in a Parallel Circuit METHOD 2: If only two resistors connected in parallel, total resistance ( R T ) can be found Substituting 3 ohms for R 1 and 4 amperes for R 2 : R T = (3 × 4)/(3 + 4) = 12/7 = 1.7 Ω

75. Determining Total Resistance in a Parallel Circuit METHOD 2: If only two resistors connected in parallel, total resistance ( R T ) can be found Total resistance (1.7 Ω) smaller than that of the smallest-resistance leg of circuit.

76. Determining Total Resistance in a Parallel Circuit METHOD 2: If only two resistors connected in parallel, total resistance ( R T ) can be found Formula can be used for more than two resistances in parallel, but only two resistances can be calculated at a time

77. Determining Total Resistance in a Parallel Circuit METHOD 2: If only two resistors connected in parallel, total resistance ( R T ) can be found After solving for R T for two resistors, use value of R T as R 1 and additional resistance in parallel as R 2

78. Determining Total Resistance in a Parallel Circuit METHOD 3: Formula to find total resistance for any number of resistances in parallel 1/ R T = 1/ R 1 + 1/ R 2 + 1/ R 3 + . . .

79. Figure 41-15 A parallel circuit with three resistors connected to a 12-volt battery.

80. Determining Total Resistance in a Parallel Circuit METHOD 3: Formula to find total resistance for any number of resistances in parallel To solve for R T for the three resistance legs substitute values of resistances for R 1 , R 2 , and R 3 : 1/ R T = 1/3 + 1/4 + 1/6 or

81. Determining Total Resistance in a Parallel Circuit METHOD 3: Formula to find total resistance for any number of resistances in parallel To solve for R T for the three resistance legs substitute values of resistances for R 1 , R 2 , and R 3 : 1/ R T = 4/12 + 3/12 + 2/12 = 9/12

82. Determining Total Resistance in a Parallel Circuit METHOD 3: Formula to find total resistance for any number of resistances in parallel To solve for R T for the three resistance legs substitute values of resistances for R 1 , R 2 , and R 3 : Cross multiplying R T = 12/9 = 1.33 Ω

83. Determining Total Resistance in a Parallel Circuit METHOD 3: Formula to find total resistance for any number of resistances in parallel Note that result (1.33 Ω) is same regardless of method used

84. Determining Total Resistance in a Parallel Circuit METHOD 4: Same as Method 3, but using electronic calculator

85. Figure 41-16 Using an electronic calculator to determine the total resistance of a parallel circuit.

86. Figure 41-17 Another example of how to use an electronic calculator to determine the total resistance of a parallel circuit. The answer is 13.45 ohms. Notice that the effective resistance of this circuit is less than the resistance of the lowest branch (20 ohms).

87. Determining Total Resistance in a Parallel Circuit METHOD 5: Can be used whenever two or more resistances connected in parallel are same value

88. Figure 41-18 A parallel circuit containing four 12-ohm resistors. When a circuit has more than one resistor of equal value, the total resistance can be determined by simply dividing the value of the resistance (12 ohms in this example) by the number of equal-value resistors (4 in this example) to get 3 ohms.

89. Determining Total Resistance in a Parallel Circuit METHOD 5: Can be used whenever two or more resistances connected in parallel are same value To calculate total resistance ( R T ) of equal-value resistors, divide number of equal resistors into value of resistance R T = Value of equal resistance/Number of equal resistances = 12 Ω/4 = 3 Ω

90. PARALLEL CIRCUIT EXAMPLES

91. Parallel Circuit Examples Each example includes solving for: Total resistance Current flow (amperes) through each branch as well as total current flow Voltage drop across each resistance

92. Figure 41-19 Example 1.

93. Parallel Circuit Examples Example 1: Voltage of battery unknown Use E = I × R ( R is total resistance of the circuit) Using equation for two resistors in parallel, total resistance is 6 ohms

94. Parallel Circuit Examples Example 1: Voltage of battery unknown Placing value of total resistors into equation results in value for battery voltage of 12 volts E = I × R E = 2 A × 6 Ω E = 12 volts

95. Figure 41-20 Example 2.

96. Parallel Circuit Examples Example 2: Value of R 3 unknown Voltage (12 volts) and current (12 A) known Solve for unknown resistance by treating each branch as separate circuit

97. Parallel Circuit Examples Example 2: Value of R 3 unknown Kirchhoff’s law: total current equals total current flow through each branch R 1 current flow is 3 A ( I = E / R = 12 V/4 Ω = 3 A)

98. Parallel Circuit Examples Example 2: Value of R 3 unknown Kirchhoff’s law: total current equals total current flow through each branch R 2 current flow is 6 A ( I = E / R = 12 V/2 Ω = 6 A)

99. Parallel Circuit Examples Example 2: Value of R 3 unknown Kirchhoff’s law: total current equals total current flow through each branch Total current through R 1 and R 2 is 9 A (3 A + 6 A = 9 A)

100. Parallel Circuit Examples Example 2: Value of R 3 unknown Kirchhoff’s law: total current equals total current flow through each branch Because 12 A leaving and returning to battery, current flow through R 3 must be 3 A (12 A – 9 A = 3 A)

101. Parallel Circuit Examples Example 2: Value of R 3 unknown Kirchhoff’s law: total current equals total current flow through each branch Resistance 4 Ω because current through unknown resistance is 3 A ( I = E / R = 12 V/4 Ω = 3 A)

102. Figure 41-21 Example 3.

103. Parallel Circuit Examples Example 3: Voltage of battery unknown To solve for voltage according to Ohm’s law: E = I × R R refers to total resistance

104. Parallel Circuit Examples Example 3: Voltage of battery unknown Four resistors of equal value; total voltage determined by: R Total = Value of Resistors/Number of Equal Resistors R = 12 Ω/4 = 3 Ω

105. Parallel Circuit Examples Example 3: Voltage of battery unknown Inserting value of total resistance of parallel circuit (3 Ω) into Ohm’s law results in battery voltage of 12 V E = 4 A × 3 Ω

106. Parallel Circuit Examples Example 3: Voltage of battery unknown Inserting value of total resistance of parallel circuit (3 Ω) into Ohm’s law results in battery voltage of 12 V E = 12 V

107. Figure 41-22 Example 4.

108. Parallel Circuit Examples Example 4: Unknown is amount of current in circuit Ohm’s law equation for determining current: I = E / R R represents total resistance

109. Parallel Circuit Examples Example 4: Unknown is amount of current in circuit The two equal resistances (8 Ω) can be replaced by one 4 Ω resistance ( R Total = Value/Number = 8 Ω/2 × 4 Ω)

110. Parallel Circuit Examples Example 4: Unknown is amount of current in circuit Total resistance of parallel circuit containing two 8-ohm resistors and one 4-ohm resistor is 2 ohms Two 8 ohm resistors in parallel equals one 4 ohm resistor

111. Parallel Circuit Examples Example 4: Unknown is amount of current in circuit Total resistance of parallel circuit containing two 8-ohm resistors and one 4-ohm resistor is 2 ohms Reduces to two 4 ohm resistors in parallel, which equals 2 ohms

112. Parallel Circuit Examples Example 4: Unknown is amount of current in circuit Current flow from battery then calculated to be 6 A I = E / R = 12 V/2 Ω = 6 A

113. SERIES-PARALLEL CIRCUITS

114. Series-Parallel Circuits Combination of series and parallel segments in one complex circuit Includes parallel resistances plus additional resistances connected in series

115. Series-Parallel Circuits Two basic types of series-parallel circuits Circuit where load is in series with other loads in parallel Example: Dash light dimming circuit

116. Series-Parallel Circuits Two basic types of series-parallel circuits Circuit where load is in series with other loads in parallel Variable resistor used to limit current flow to dash light bulbs, which are wired in parallel

117. Figure 41-23 A series-parallel circuit.

118. Series-Parallel Circuits Two basic types of series-parallel circuits Circuit where parallel circuit contains resistors in series with one or more branches Example: Headlight and starter circuit

119. Series-Parallel Circuits Two basic types of series-parallel circuits Circuit where parallel circuit contains resistors in series with one or more branches Headlight switch usually connected in series with dimmer switch and in parallel with dash light dimmer resistors

120. Series-Parallel Circuits Two basic types of series-parallel circuits Circuit where parallel circuit contains resistors in series with one or more branches Headlights also connected in parallel with taillights and side marker lights

121. Figure 41-24 This complete headlight circuit with all bulbs and switches is a series-parallel circuit.

122. Series-Parallel Circuits Series-Parallel Circuit Faults Conventional parallel circuit, such as taillight, has electrical fault that increases resistance in one branch

123. Series-Parallel Circuits Series-Parallel Circuit Faults Amount of current flow through that branch reduced Added resistance creates voltage drop

124. Series-Parallel Circuits Series-Parallel Circuit Faults Lower voltage applied and single taillight is dimmer If added resistance occurs in part of circuit feeding both taillights, both taillights would be dimmer

125. Series-Parallel Circuits Series-Parallel Circuit Faults Added resistance creates series-parallel circuit from original parallel circuit

126. SOLVING SERIES-PARALLEL CIRCUIT PROBLEMS

127. Solving Series-Parallel Circuit Problems Combine or simplify as much as possible If two resistances in series within parallel branch Simplify circuit by adding two together before attempting to solve parallel section

128. Figure 41-25 Solving a series-parallel circuit problem.

129. SERIES-PARALLEL CIRCUIT EXAMPLES

130. Series-Parallel Circuit Examples Each example includes solving for: Total resistance Current flow (amperes) through each branch, as well as total current flow Voltage drop across each resistance

131. Figure 41-26 Example 1.

132. Series-Parallel Circuit Examples Example 1: Unknown resistor in series with other two resistances, connected in parallel Ohm’s law equation to determine resistance: R = E / I = 12 V/3 A = 4 Ω Total resistance of circuit 4 ohms

133. Series-Parallel Circuit Examples Example 1: Unknown resistor in series with other two resistances, connected in parallel Value of unknown determined by subtracting value of two resistors connected in parallel; parallel branch resistance is 2 Ω.

134. Series-Parallel Circuit Examples Example 1: Unknown resistor in series with other two resistances, connected in parallel Value of unknown resistance is 2 Ω Total R = 4 Ω – 2 Ω = 2 Ω

135. Figure 41-27 Example 2.

136. Series-Parallel Circuit Examples Example 2: Unknown is voltage of battery Ohm’s law equation: E = I × R Before solving, determine total resistance Each branch contains two 4-ohm resistors in series

137. Series-Parallel Circuit Examples Example 2: Unknown is voltage of battery Before solving, determine total resistance Add value in each branch to simplify circuit

138. Series-Parallel Circuit Examples Example 2: Unknown is voltage of battery Before solving, determine total resistance Parallel circuit now consists of two 8-ohm resistors

139. Series-Parallel Circuit Examples Example 2: Unknown is voltage of battery

140. Series-Parallel Circuit Examples Example 2: Unknown is voltage of battery Inserting value for total resistance into equation results in value of 12 V for battery voltage E = I × R

141. Series-Parallel Circuit Examples Example 2: Unknown is voltage of battery Inserting value for total resistance into equation results in value of 12 V for battery voltage E = 3 A × 4 Ω

142. Series-Parallel Circuit Examples Example 2: Unknown is voltage of battery Inserting value for total resistance into equation results in value of 12 V for battery voltage E = 12 volts

143. Figure 41-28 Example 3.

144. Series-Parallel Circuit Examples Example 3: Total current through circuit unknown Ohm’s law equation: I = E / R Before solving, determine total resistance of parallel circuit

145. Series-Parallel Circuit Examples Example 3: Total current through circuit unknown First simplify circuit by adding R 3 and R 4 (in series in same branch of parallel circuit)

146. Series-Parallel Circuit Examples Example 3: Total current through circuit unknown Resulting parallel section of circuit, now containing two 8-ohm resistors in parallel, can be replaced with one 4-ohm resistor

147. Series-Parallel Circuit Examples Example 3: Total current through circuit unknown

148. Series-Parallel Circuit Examples Example 3: Total current through circuit unknown Add 4-ohm resistor to 2-ohm ( R 1 ) resistor in series Total circuit resistance 6 ohms

149. Series-Parallel Circuit Examples Example 3: Total current through circuit unknown Determine current flow from Ohm’s law: I = E / R = 12 V/6 Ω = 2 A

150. Figure 41-29 Example 4.

151. Series-Parallel Circuit Examples Example 4: Value of resistor R 1 unknown Using Ohm’s law, total resistance of circuit 3 ohms R = E / I = 12 V/4 A = 3 Ω

152. Series-Parallel Circuit Examples Example 4: Value of resistor R 1 unknown Knowing total resistance not enough to determine value of R 1 R 2 and R 5 in series; combine to create 8-ohm parallel branch resistance Reduce the two 8-ohm branches to one 4-ohm branch

153. Series-Parallel Circuit Examples Example 4: Value of resistor R 1 unknown

154. Series-Parallel Circuit Examples Example 4: Value of resistor R 1 unknown Circuit simplified to one resistor in series ( R 1 ) with two 4-ohm branches Two 4-ohm branches can be reduced to one 2-ohm resistor

155. Series-Parallel Circuit Examples Example 4: Value of resistor R 1 unknown

156. Series-Parallel Circuit Examples Example 4: Value of resistor R 1 unknown Now circuit includes one 2-ohm resistor plus unknown R 1 Because total resistance 3 ohms, value of R 1 must be 1 ohm 3 Ω – 2 Ω = 1 Ω

157. TECH TIP Farsighted Quality of Electricity Electricity almost seems to act as if it “knows” what resistances are ahead on the long trip through a circuit. If the trip through the circuit has many high-resistance components, very few electrons (amperes) will choose to attempt to make the trip. BACK TO PRESENTATION If a circuit has little or no resistance (for example, a short circuit), then as many electrons (amperes) as possible attempt to flow through the complete circuit. If the flow exceeds the capacity of the fuse or the circuit breaker, then the circuit is opened and all current flow stops.

158. FREQUENTLY ASKED QUESTION Why Check the Voltage Drop Instead of Measuring the Resistance? Imagine a wire with all strands cut except for one. An ohmmeter can be used to check the resistance of this wire and the resistance would be low, indicating that the wire was okay. But this one small strand cannot properly carry the current (amperes) in the circuit. ? BACK TO PRESENTATION A voltage drop test is therefore a better test to determine the resistance in components for two reasons: An ohmmeter can only test a wire or component that has been disconnected from the circuit and is not carrying current. The resistance can, and does, change when current flows. A voltage drop test is therefore a better test to determine the resistance in components for two reasons: A voltage drop test is a dynamic test because as the current flows through a component, the conductor increases in temperature, which in turn increases resistance. This means that a voltage drop test is testing the circuit during normal operation and is therefore the most accurate way of determining circuit conditions. A voltage drop test is also easier to perform because the resistance does not have to be known, only that the unwanted loss of voltage in a circuit should be less than 3% or less than about 0.14 volts for any 12-volt circuit.

159. TECH TIP The Path of Least Resistance There is an old saying that electricity will always take the path of least resistance. This is true, especially if there is a fault such as in the secondary (high-voltage) section of the ignition system. If there is a path to ground that is lower than the path to the spark plug, the high-voltage spark will take the path of least resistance. BACK TO PRESENTATION In a parallel circuit where there is more than one path for the current to flow, most of the current will flow through the branch with the lower resistance. This does not mean that all of the current will flow through the lowest resistance, because the other path does provide a path to ground, and the amount of current flow through the other branches is determined by the resistance and the applied voltage according to Ohm’s law. Therefore, the only place where electricity takes the path of least resistance is in a series circuit where there are not other paths for the current to flow.