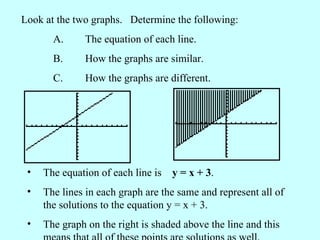
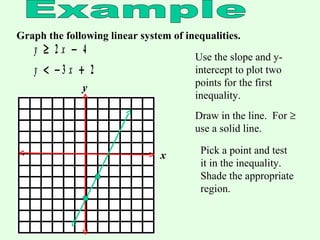
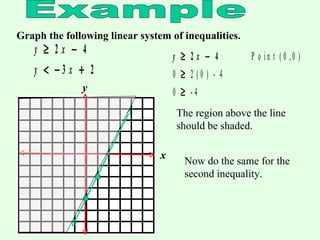
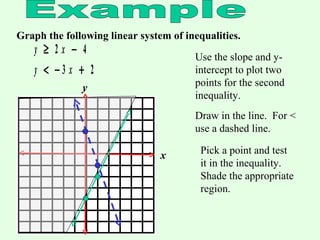
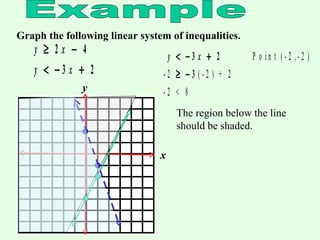
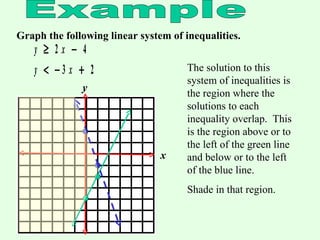
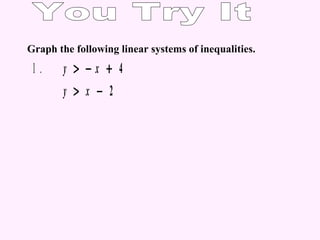
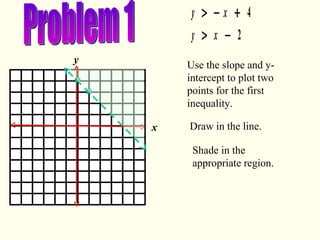
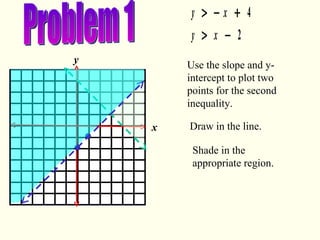
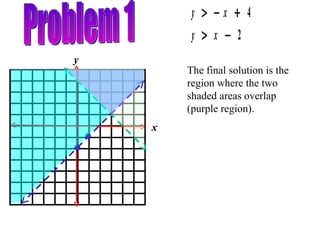
This document provides instructions for graphing systems of linear inequalities. It explains how to write inequalities in slope-intercept form, plot points to draw the line, and shade the appropriate region based on whether it is <, ≤, >, or ≥. An example problem is worked through step-by-step to demonstrate how to graph two inequalities and find the overlapping region that satisfies both inequalities. Practice problems are then provided for the reader to work through on their own.

1. Graphing Systems of Inequalities

2. Look at the two graphs. Determine the following: A. The equation of each line. B. How the graphs are similar. C. How the graphs are different. The equation of each line is y = x + 3 . The lines in each graph are the same and represent all of the solutions to the equation y = x + 3. The graph on the right is shaded above the line and this means that all of these points are solutions as well.

3. Inequalities with Greater Than Pick a point from the shaded region and test that point in the equation y = x + 3 . Point: (-4, 5) This is incorrect. Five is greater than or equal to negative 1. If a solid line is used, then the equation would be 5  -1 . If a dashed line is used, then the equation would be 5 > -1 . The area above the line is shaded .

4. Inequalities with Less Than Pick a point from the shaded region and test that point in the equation y = -x + 4 . Point: (1, -3) This is incorrect. Negative three is less than or equal to 3. If a solid line is used, then the equation would be -3  3 . If a dashed line is used, then the equation would be -3 < 3 . The area below the line is shaded .

5. Graphing Linear Inequalities Write the inequality in slope-intercept form. Use the slope and y-intercept to plot two points. Draw in the line. Use a solid line for less than or equal to (  ) or greater than or equal to (  ). Use a dashed line for less than (<) or greater than (>). Pick a point above the line or below the line. Test that point in the inequality. If it makes the inequality true, then shade the region that contains that point. If the point does not make the inequality true, shade the region on the other side of the line. Systems of inequalities – Follow steps 1-4 for each inequality. Find the region where the solutions to the two inequalities would overlap and this is the region that should be shaded.

6. Example Graph the following linear system of inequalities. Use the slope and y-intercept to plot two points for the first inequality. Draw in the line. For  use a solid line. Pick a point and test it in the inequality. Shade the appropriate region. x y

7. Example Graph the following linear system of inequalities. The region above the line should be shaded. Now do the same for the second inequality. x y

8. Example Graph the following linear system of inequalities. Use the slope and y-intercept to plot two points for the second inequality. Draw in the line. For < use a dashed line. Pick a point and test it in the inequality. Shade the appropriate region. x y

9. Example Graph the following linear system of inequalities. The region below the line should be shaded. x y

10. Example Graph the following linear system of inequalities. The solution to this system of inequalities is the region where the solutions to each inequality overlap. This is the region above or to the left of the green line and below or to the left of the blue line. Shade in that region. x y

11. You Try It Graph the following linear systems of inequalities.

12. Problem 1 Use the slope and y-intercept to plot two points for the first inequality. Draw in the line. Shade in the appropriate region. x y

13. Problem 1 Use the slope and y-intercept to plot two points for the second inequality. Draw in the line. Shade in the appropriate region. x y

14. Problem 1 The final solution is the region where the two shaded areas overlap (purple region). x y