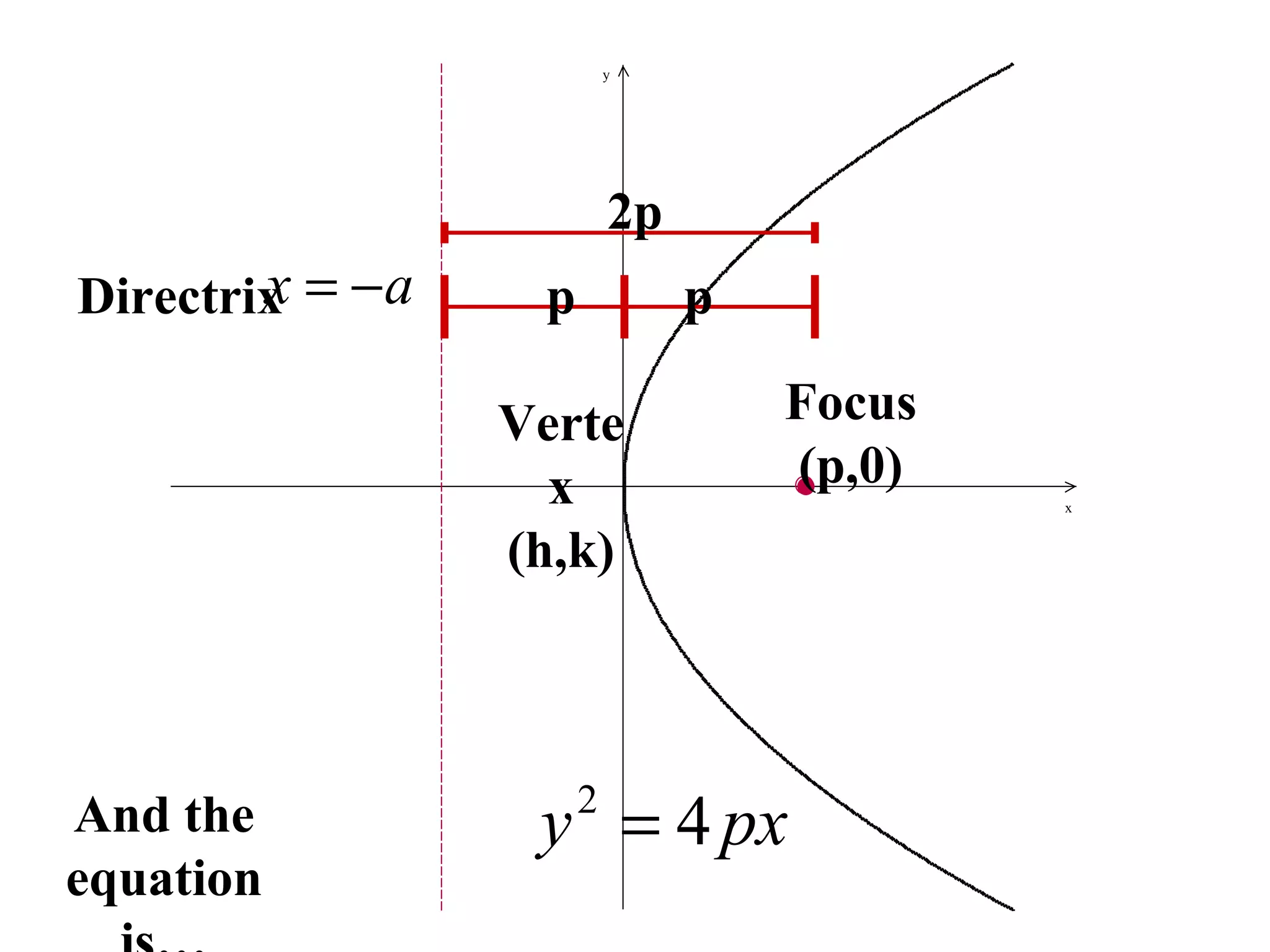
The document defines a parabola geometrically as the set of all points in a plane that are the same distance from a fixed point, called the focus, as they are from a fixed line, called the directrix. It provides examples of parabolas in standard form with the vertex at various points and opening in different directions. It also discusses how to write the standard form equation of a parabola given its focus and vertex, as well as how to find the focus and directrix of a parabola given its equation. Finally, it demonstrates how to use the method of completing the square to convert a general quadratic equation into the standard form needed for graphing a parabola.

2. Geometric Definition of a Parabola: The collection of
all the points P(x,y) in a a plane that are the same
distance from a fixed point, the focus, as they are from
a fixed line called the directrix.
y
Focus
(0,p) P
x
Verte
x
(h,k)

3. y As you can plainly see
the distance from the
focus to the vertex is a
and is the same distance
from the vertex to the
directrix! Neato!
Focus
(0,p) p
2p x
Verte
x p
Directrix y = -p
(h,k)
And the
equation x = 4 py
2
is…

4. y
Directrix = a
y
Verte p
x x
(h,k)
p
Focus
(0,-p)
And the
equation
x = −4 py
2
is…

5. y
2p
Directrix = −a
x p p
Verte Focus
x (p,0)
x
(h,k)
And the y = 4 px
2
equation

6. y
p p
Vertex
Directrix = a
x
Focus (- (h,k)
p,0)
x
And the y = −4 px
2
equation

7. STANDARD FORMS
Vertex at (h, k )
1) ( x − h) 2 = 4 p ( y − k )
Opens up
Vertex at (h, k )
2) ( x − h) 2 = −4 p ( y − k )
Opens down
Vertex at (h, k )
3) ( y − k ) 2 = 4 p ( x − h)
Opens right
Vertex at (h, k )
4) ( y − k ) = −4 p ( x − h)
2
Opens left
I like to call standard form “Good Graphing Form”

8. Graphing an Equation of a Parabola
Standard Equation of a Parabola (Vertex at Origin)
x = 4 py
2
x = 12 y
2
( 0, p )
focus ( 0, 3)
y = −p
directrix
y = −3

9. Graphing an Equation of a Parabola
Standard Equation of a Parabola (Vertex at Origin)
y = 4 px
2
y = 12 x
2
( p, 0 )
focus ( 3, 0 )
x = −p
directrix
x = −3

10. Graphing an Equation of a Parabola
Graph the equation. Identify the focus and directrix of the
parabola.
1. x = 2 y
2
1
4p = 2 p =
2
 1
focus:  0, 
 2
1
directrix: y = −
2

11. Graphing an Equation of a Parabola
Graph the equation. Identify the focus and directrix of the
parabola.
2. y = 16 x
2
4 p = 16 p = 4
focus: ( 4, 0 )
directrix: x = −4

12. Graphing an Equation of a Parabola
Graph the equation. Identify the focus and directrix of the
parabola.
1
3. x = − y
2
1 4 1
4p = − p = −
4 16
 1
focus:  0, − 
 16 
1
directrix: y =
16

13. Graphing an Equation of a Parabola
Graph the equation. Identify the focus and directrix of the
parabola.
4. y = −4 x
2
4 p = −4 p = −1
focus: ( − 1, 0 )
directrix: x = 1

14. Writing an Equation of a Parabola
Write the standard form of the equation of the parabola
with the given focus and vertex at (0, 0).
5. 0, 1( ) x = 4 py
2
x = 4( 1 ) y
2
x = 4y
2
 1 
6.  − , 0  y = 4 px
2
 2 
y 2
=4−
1
2
( )x y = −2 x
2

15. Writing an Equation of a Parabola
Write the standard form of the equation of the parabola
with the given focus and vertex at (0, 0).
7. ( − 2, 0 ) y = 4 px
2
y = 4( − 2) x y = −8 x
2 2
 1
8.  0,  x = 4 py
2
 4
1
x = 4(
2
4
)y x =y 2

16. Modeling a Parabolic Reflector
9. A searchlight reflector is designed so
that a cross section through its axis is a
parabola and the light source is at the
focus. Find the focus if the reflector is 3
feet across at the opening and 1 foot deep.
(1x5) = 4 p (1)
. 2 2
y
2.25 = 4 p
(1.5, 1) p = 2.25 = 9
225
4
400 16

17. Notes Over 10.2
Modeling a Parabolic Reflector
10. One of the largest radio telescopes has
a diameter of 250 feet and a focal length
of 50 feet. If the cross section of the radio
telescope is a parabola, find the depth.
x = 4 py
2 250
= 125
x = 4( 50 ) y
2
2
x = 200 y 15,625 = 200 y
2
125 = 200 y
2
y = 78.1 ft

18. General Form of any Parabola
Ax + By + Cx + Dy + E = 0
2 2
*Where either A or B is zero!
* You will use the “Completing the
Square” method to go from the
General Form to Standard Form,

19. Graphing a Parabola: Use completing the square
to convert a general form equation to standard
conic form
General form
y2 - 10x + 6y - 11 = 0
y2 + 6y + 9 = 10x + 11 + _____
9
(y + 3)2 = 10x + 20
(y + 3)2 = 10(x + 2)
Standard form
aka: Graphing form
(y-k)2 = 4p(x-h)