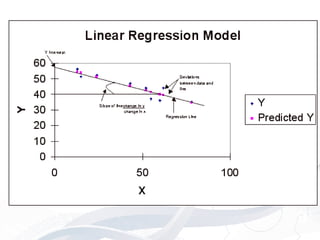
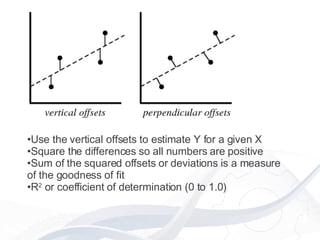
This document provides an overview of statistical modeling techniques using real data, including correlation, linear regression, and interpreting regression outputs in Excel. It discusses measuring the strength of relationships between variables, using linear regression to find relationships between a dependent variable and independent variables, and how to perform correlation and regression analyses in Excel using a sample dataset with income, education and age variables. Potential errors in modeling are also noted.

1. Teaching Basic Modeling Skills Using Real Data Steven Gordon Senior Director of Education and Client Services [email_address]

2. Goals of the Session Overview of statistical methods that can be used to build a model Sources of real data to test hypotheses about statistical relationships Example exercise(s) and techniques for downloading and extracting data, testing statistical relationships, and building a model based on the results

3. Measuring the Strength of a Relationship Correlation Statistical relationship between two variables Goes between -1.0 and 1.0 Zero means no relationship http://argyll.epsb.ca/jreed/math9/strand4/scatterPlot.htm

4. Linear Regression Assumes a cause and effect between one dependent variable and one or more independent variables Solution of the linear equation with a best fit to data Y = aX + b where: Y = the dependent variable a = a coefficient equivalent to the slope of the line b = the Y intercept of the line (the place where it crosses the Y axis) Y = a 1 X 1 + a 2 X 2 + a 3 X 3 + b for multiple causes

6. Use the vertical offsets to estimate Y for a given X Square the differences so all numbers are positive Sum of the squared offsets or deviations is a measure of the goodness of fit R 2 or coefficient of determination (0 to 1.0)

7. Using Excel for Regression Analysis Open the file Regress_Data.xls File shows a dataset with 40 observations showing Income, Education, and Age What would we hypothesize to be the relationships? Which is the dependent variable? Independent variables? Need to activate the data analysis toolpak Click on Tools from main menu in Excel – if Data Analysis is a submenu choice – good to go Otherwise – Select Tools> Add-Ins Mark the box next to the Analysis Toolpak and click OK

8. Do a Correlation Analysis Click on Tools – Data Analysis Choose Correlation from the pull-down menu Click in the input range box Choose all three columns including the labels by clicking and dragging across the entire dataset Click the Labels box to indicate the first row is labels Click New Worksheet and give it a name correlate What are the results?

9. Do a Regression Click Tools, Data Analysis Select Regression from the pull down menu Put your cursor in the field for the input Y Range Select the range for the dependent variable, including its label Put the cursor in the Input X Range Select the other two columns of number Mark the check boxes Labels Confidence Level Click on the radio button for New Worksheet and give it a name Click ok

10. Interpreting Regression Outputs in Excel 37.6 percent of variance explained after adjusting for degrees of freedom

11. More interpretation Significance of the equation. Probability of a false positive is less than 0.004 %

12. Coefficients and Their Significance Equation: Income = -17954.1 + 440.71*Age+ 1542.41*Education Significance of individual coefficients

13. Fitting Non-Linear Data Same principle and measurement of the deviations Choice of curve to fit not automatic Individual choice with possibility of error Real relationship may not be fully represented by experimental data

14. Potential Errors Chose the wrong function for non-linear data Experiments did not measure all possible circumstances Behavior may change in areas outside the sample data E.G. physical limitations of system lead to failure Variables may be highly correlated and have strong relationship in regression but one is not the cause of the other

15. Exercise Using Real Data