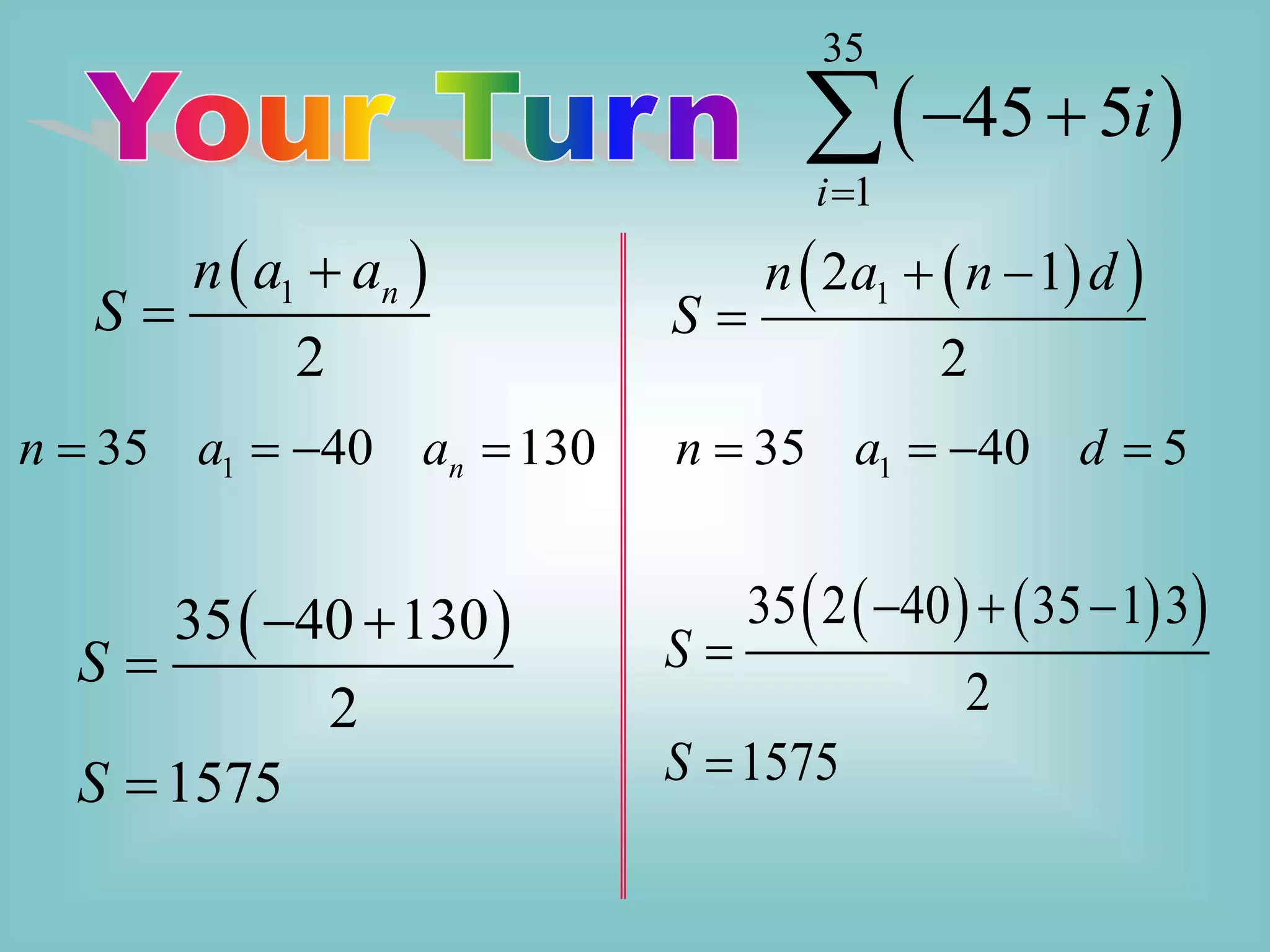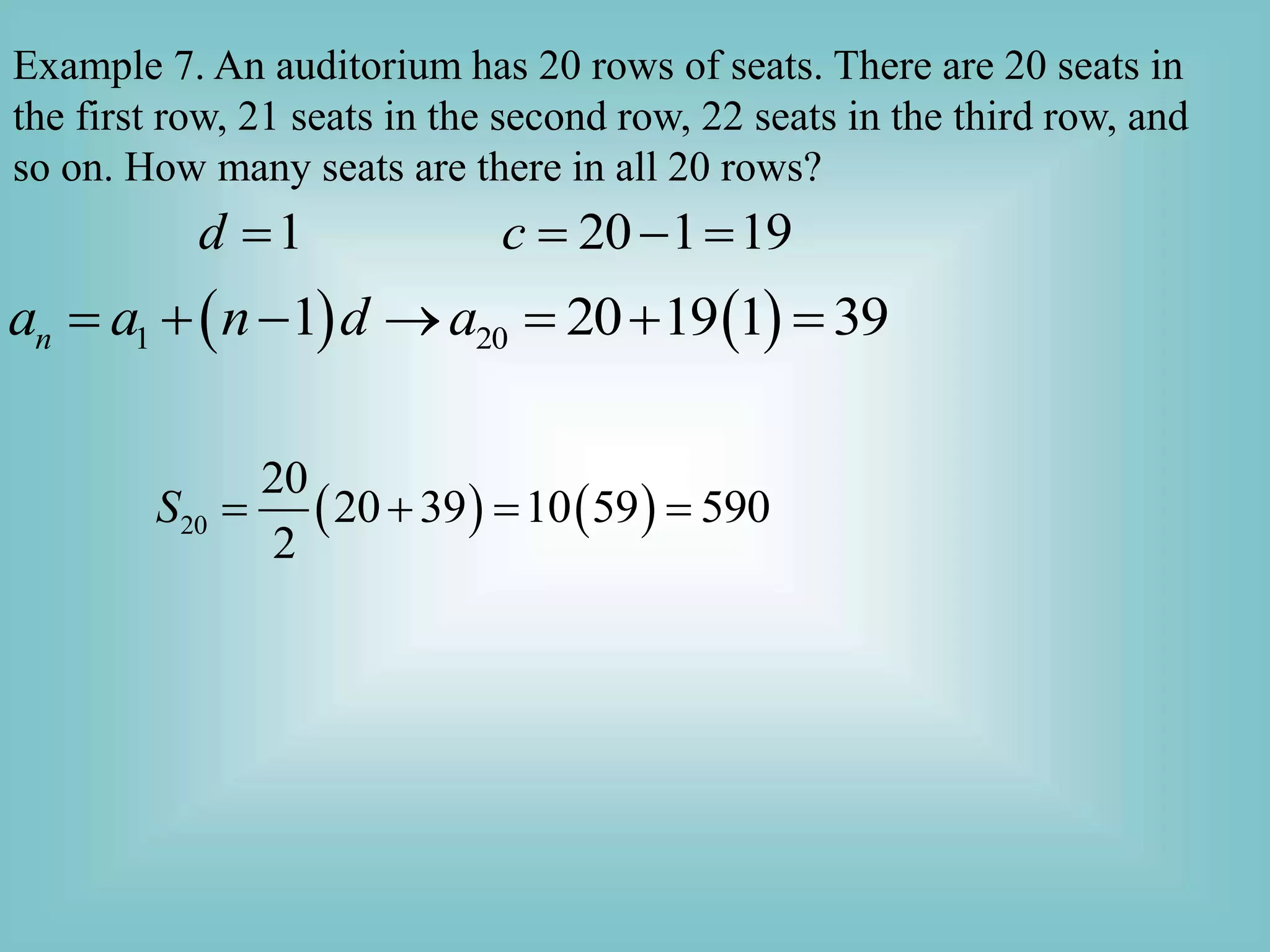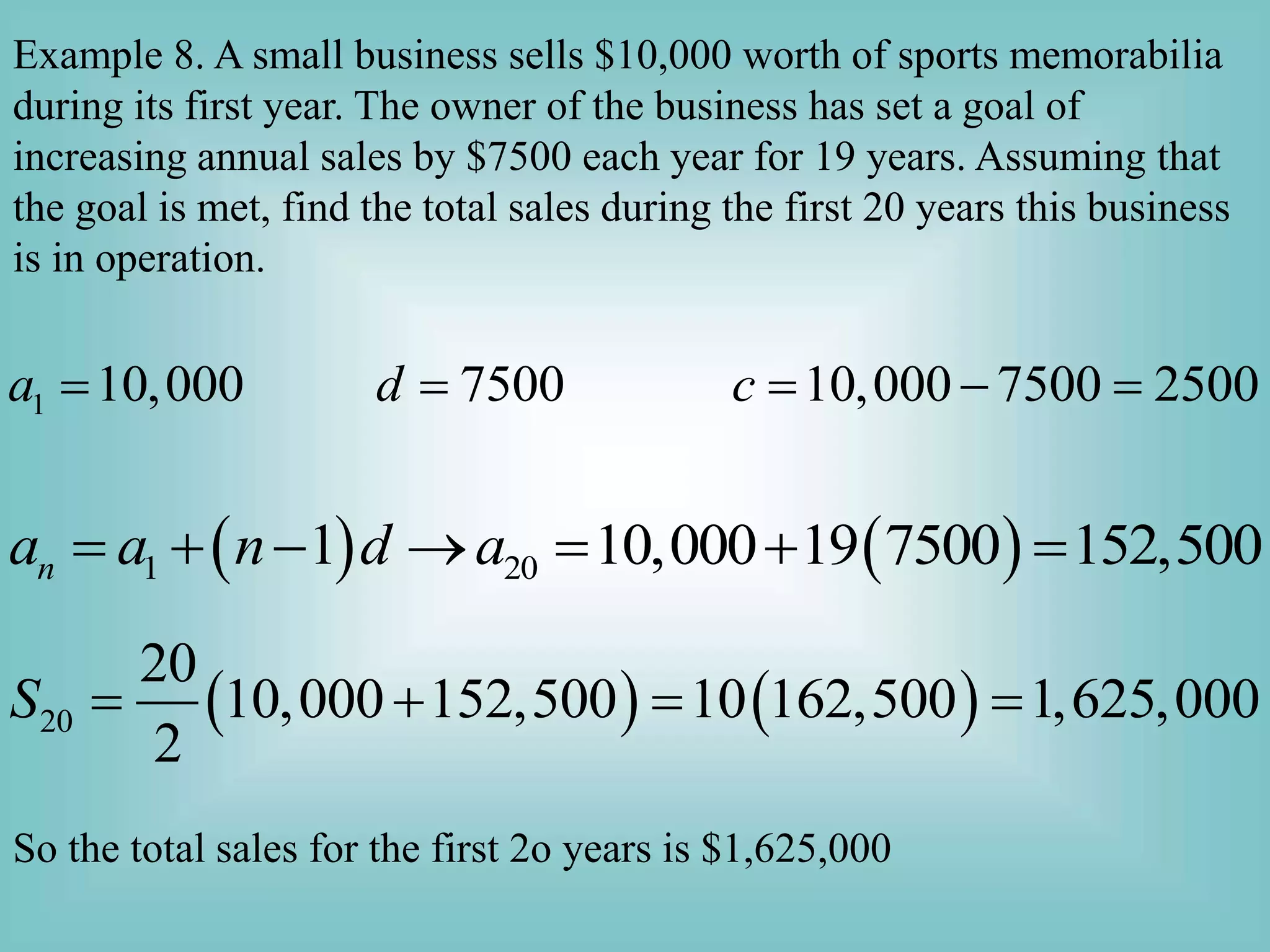The document discusses arithmetic sequences and series. Some key points include: - An arithmetic sequence is defined as a sequence where the difference between consecutive terms is constant. This constant difference is called the common difference. - Formulas are provided for finding the nth term of an arithmetic sequence and the sum of the first n terms of an arithmetic sequence. - Examples are given of identifying arithmetic sequences based on patterns of terms and solving problems using the formulas, such as finding missing terms or sums.

1. Arithmetic
Sequences
and Series

2. Sequences Series
List with commas “Indicated sum”
3, 8, 13, 18 3 + 8 + 13 + 18

4. An Arithmetic Sequence is
defined as a sequence in
which there is a common
difference between
consecutive terms.

5. Which of the following sequences are
arithmetic? Identify the common
difference.
3, 1, 1, 3, 5, 7, 9, . . .
 
15.5, 14, 12.5, 11, 9.5, 8, . . .
84, 80, 74, 66, 56, 44, . . .
8, 6, 4, 2, 0, . . .
 
50, 44, 38, 32, 26, . . .
    
YES 2
d 
YES
YES
NO
NO
1.5
d  
6
d 

6. 26, 21, 16, 11, 6, . . .
    

7. The general form of an ARITHMETIC sequence.
1
a
First Term:
Second Term: 2 1
a a d
 
Third Term:
Fourth Term:
Fifth Term:
3 1 2
a a d
 
4 1 3
a a d
 
5 1 4
a a d
 
nth Term:  
1 1
n
a a n d
  

8. Formula for the nth term of an ARITHMETIC
sequence.
 
1 1
n
a a n d
  
The nth term
n
a 
The term number
n 
The common difference
d 
1 The 1st term
a 

9. Given: 79, 75, 71, 67, 63, . . .
Find: 32
a
1 79
4
32
a
d
n

 

 
  
1
32
32
1
79 32 1 4
45
n
a a n d
a
a
  
   
 
IDENTIFY SOLVE

10. Given: 79, 75, 71, 67, 63, . . .
Find: What term number is -169?
1 79
4
169
n
a
d
a

 
 
 
  
1 1
169 79 1 4
63
n
a a n d
n
n
  
    

IDENTIFY SOLVE

11. Given:
10
12
3.25
4.25
a
a


1
3
3.25
4.25
3
a
a
n



 
 
1 1
4.25 3.25 3 1
0.5
n
a a n d
d
d
  
  

IDENTIFY SOLVE
Find: 1
a
What’s the real question? The Difference

12. Given:
10
12
3.25
4.25
a
a


10 3.25
0.5
10
a
d
n



 
 
1
1
1
1
3.25 10 1 0.5
1.25
n
a a n d
a
a
  
  
 
IDENTIFY SOLVE
Find: 1
a

14.  
50
1
73 2
p
p


    
71 69 67 . . . 25 27
       

15.    
71 69 67 . . . 25 27
      
   
27 25 . . . 67 69 71
      
44 44 44 . . . 44 44 44
     
 
 
50 71 27
2
 

1100

71 + (-27) Each sum
is the same.
50 Terms

16.      
 
1 1 1 1
2 . . . 1
a a d a d a n d
       
 
     
1 1 1 1
1 . . . 2
a n d a d a d a
       
 
1
2
n
n a a
s 

1
Sum
Number of Terms
First Term
Last Term
n
S
n
a
a


 




 

 
   
   
 
1 1 1 1 1 1
1 1 . . . 1
a a n d a a n d a a n d
           
     
     

17. Find the sum of the terms of this
arithmetic series.
 
35
1
29 3
k
k

 

 
1
2
n
n a a
S


1
35
35
26
76
n
a
a

 

 
35 26 76
2
875
S
S
 



18. Find the sum of the terms of this arithmetic
series.  
151 147 143 139 . . . 5
     
 
1
2
n
n a a
S


1
40
40
151
5
n
a
a


 
 
40 151 5
2
2920
S
S
 


 
  
1 1
5 151 1 4
40
n
a a n d
n
n
  
    

What term is -5?

19.  
1
2
n
n a
S
a


 
1 1
Substitute n
a a n d
  
 
 
 
 
1 1
1
1
2
2 1
2
n a a n d
S
n a n d
S
  

 

1
# of Terms
1st Term
Difference
n
a
d





 


20. Find the sum of this series  
36
0
2.25 0.75
j
j



2.25 3 3.73 4.5 . . .
    
 
 
1
2 1
2
n a n d
S
 

1
37
2.25
0.75
n
a
d



    
 
37 2 2.25 37 1 0.75
2
582.75
S
S
 



21.  
35
1
45 5
i
i

 

 
1
2
n
n a a
S


 
 
1
2 1
2
n a n d
S
 

1
35 40 130
n
n a a
    1
35 40 5
n a d
   
 
35 40 130
2
1575
S
S
 


   
 
35 2 40 35 1 3
2
1575
S
S
  



22. An introduction…………
1, 4, 7,10,13
9,1, 7, 15
6.2, 6.6, 7, 7.4
, 3, 6
 
    
Arithmetic Sequences
ADD
To get next term
2, 4, 8,16, 32
9, 3,1, 1/3
1,1/ 4,1/16,1/ 64
, 2.5 , 6.25
 
  
Geometric Sequences
MULTIPLY
To get next term
Arithmetic Series
Sum of Terms
35
12
27.2
3 9

 
Geometric Series
Sum of Terms
62
20/3
85/ 64
9.75

23. Find the next four terms of –9, -2, 5, …
Arithmetic Sequence
2 9 5 2 7
      
7 is referred to as the common difference (d)
Common Difference (d) – what we ADD to get next term
Next four terms……12, 19, 26, 33

24. Find the next four terms of 0, 7, 14, …
Arithmetic Sequence, d = 7
21, 28, 35, 42
Find the next four terms of x, 2x, 3x, …
Arithmetic Sequence, d = x
4x, 5x, 6x, 7x
Find the next four terms of 5k, -k, -7k, …
Arithmetic Sequence, d = -6k
-13k, -19k, -25k, -32k

25. Vocabulary of Sequences (Universal)
1
a First term

n
a nth term

n
S sum of n terms

n number of terms

d common difference

 
 
n 1
n 1 n
nth term of arithmetic sequence
sum of n terms of arithmetic sequen
a a n 1 d
n
S a a
2
ce
  
 



26. Given an arithmetic sequence with 15 1
a 38 and d 3, find a .
  
1
a First term

n
a nth term

n
S sum of n terms

n number of terms

d common difference

x
15
38
NA
-3
 
n 1
a a n 1 d
  
  
38 x 1 1
5 3
   
X = 80

27. 63
Find S of 19, 13, 7,...
  
1
a First term

n
a nth term

n
S sum of n terms

n number of terms

d common difference

-19
63
??
x
6
 
n 1
a a n 1 d
  
  
?? 19 6 1
?? 353
3 6
  


353
 
n 1 n
n
S a a
2
 
 
63
63
3 3
S
2
19 5

 
63 1 1
S 052


28. 16 1
Find a if a 1.5 and d 0.5
 
Try this one:
1
a First term

n
a nth term

n
S sum of n terms

n number of terms

d common difference

1.5
16
x
NA
0.5
 
n 1
a a n 1 d
  
 
16 1.5 0.
a 16 5
1
  
16
a 9


29. n 1
Findnif a 633, a 9, and d 24
  
1
a First term

n
a nth term

n
S sum of n terms

n number of terms

d common difference

9
x
633
NA
24
 
n 1
a a n 1 d
  
 
633 9 2
1
x 4
  
633 9 2 24
4x
  
X = 27

30. 1 29
Find dif a 6 and a 20
  
1
a First term

n
a nth term

n
S sum of n terms

n number of terms

d common difference

-6
29
20
NA
x
 
n 1
a a n 1 d
  
 
1
20 6 29 x
  

26 28x

13
x
14


31. Find two arithmetic means between –4 and 5
-4, ____, ____, 5
1
a First term

n
a nth term

n
S sum of n terms

n number of terms

d common difference

-4
4
5
NA
x
 
n 1
a a n 1 d
  
  
1
5 4 4 x
  

x 3

The two arithmetic means are –1 and 2, since –4, -1, 2, 5
forms an arithmetic sequence

32. Find three arithmetic means between 1 and 4
1, ____, ____, ____, 4
1
a First term

n
a nth term

n
S sum of n terms

n number of terms

d common difference

1
5
4
NA
x
 
n 1
a a n 1 d
  
  
4 1 x
1
5
  
3
x
4

The three arithmetic means are 7/4, 10/4, and 13/4
since 1, 7/4, 10/4, 13/4, 4 forms an arithmetic sequence

33. Find n for the series in which 1 n
a 5, d 3,S 440
  
1
a First term

n
a nth term

n
S sum of n terms

n number of terms

d common difference

5
x
y
440
3
 
n 1
a a n 1 d
  
 
n 1 n
n
S a a
2
 
 
y 5 3
1
x
  
 
x
40 y
4
2
5
 
 
 
1
2
x
440 5 5 x 3
   
 
x 7 x
440
2
3


 
880 x 7 3x
 
2
0 3x 7x 880
  
X = 16
Graph on positive window

34. The sum of the first n terms of an infinite sequence
is called the nth partial sum.
1
( )
2
n n
n
S a a
 

35. Example 6. Find the 150th partial sum of the arithmetic sequence, 5,
16, 27, 38, 49, …
1 5 11 5 11 6
a d c
      
11 6
n
a n
   
150 11 150 6 1644
a
   
   
150
150
5 1644 75 1649 123,675
2
S    

36. Example 7. An auditorium has 20 rows of seats. There are 20 seats in
the first row, 21 seats in the second row, 22 seats in the third row, and
so on. How many seats are there in all 20 rows?
1 20 1 19
d c
   
   
1 20
1 20 19 1 39
n
a a n d a
      
   
20
20
20 39 10 59 590
2
S    

37. Example 8. A small business sells $10,000 worth of sports memorabilia
during its first year. The owner of the business has set a goal of
increasing annual sales by $7500 each year for 19 years. Assuming that
the goal is met, find the total sales during the first 20 years this business
is in operation.
1 10,000 7500 10,000 7500 2500
a d c
    
   
1 20
1 10,000 19 7500 152,500
n
a a n d a
      
   
20
20
10,000 152,500 10 162,500 1,625,000
2
S    
So the total sales for the first 2o years is $1,625,000