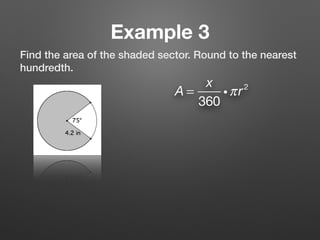
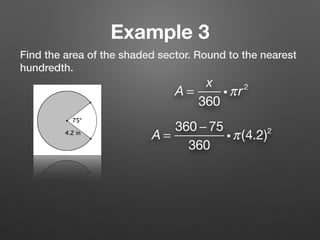
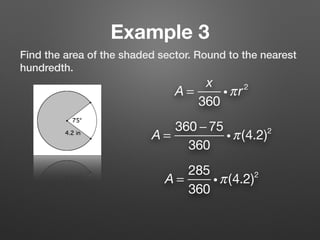
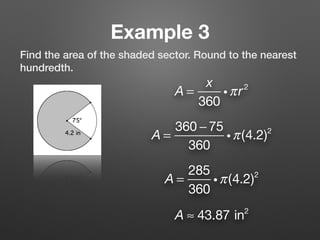
This document provides information about calculating areas of circles and sectors of circles. It defines key terms like sector and segment of a circle. It then presents 3 examples that demonstrate how to calculate the area of a full circle, sector of a circle, and segment of a circle using the appropriate formulas. The final section lists additional practice problems for students to work through.