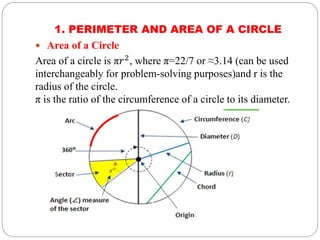
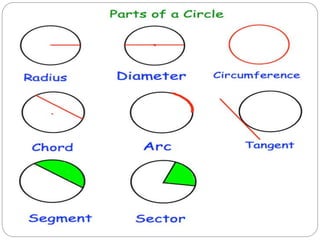
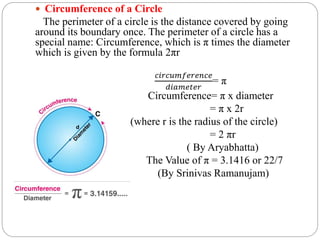
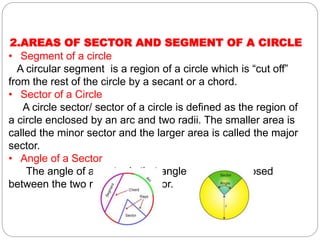
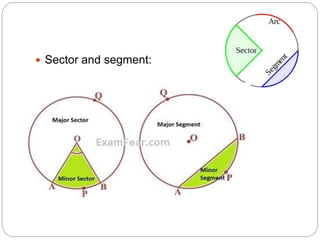
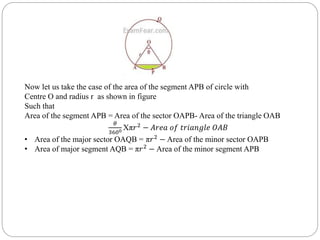
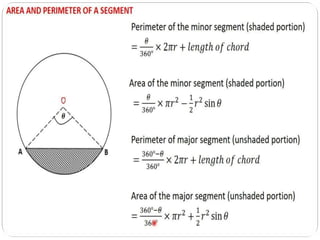
This document summarizes key concepts related to circles for a 10th grade class. It covers the perimeter and area of circles, finding the area of sectors and segments of circles, and calculating the areas of combinations of plane figures. The perimeter of a circle is called its circumference, which is 2πr. The area of a circle is πr^2. To find the area of a sector, use the formula (θ/360)×πr^2, where θ is the central angle of the sector in degrees and r is the radius. The area of combinations of shapes can be found by subtracting the area of one figure from another or adding/subtracting different areas.

1. By
Sri. Siddalingeshwara BP M.Sc, B.Ed, (P.hd)
AREAS RELATED TO CIRCLES
Chapter-10
for
class-x

2.  Content:
1.Perimeteer and Area of a Circle.
Area of a Circle
Parts of Circle
Circumference of a Circle
2.Areas of sector and segment of a Circle.
Segment of a circle
Sector of a Circle
Angle of a Sector
Length of an arc of a sector
Area of a Sector of a Circle
3.Areas of combination of Plane Figures.

3. 1. PERIMETER AND AREA OF A CIRCLE
 Area of a Circle
Area of a circle is π𝑟2, where π=22/7 or ≈3.14 (can be used
interchangeably for problem-solving purposes)and r is the
radius of the circle.
π is the ratio of the circumference of a circle to its diameter.

5.  Circumference of a Circle
The perimeter of a circle is the distance covered by going
around its boundary once. The perimeter of a circle has a
special name: Circumference, which is π times the diameter
which is given by the formula 2πr
𝑐𝑖𝑟𝑐𝑢𝑚𝑓𝑒𝑟𝑒𝑛𝑐𝑒
𝑑𝑖𝑎𝑚𝑒𝑡𝑒𝑟
= π
Circumference= π x diameter
= π x 2r
(where r is the radius of the circle)
= 2 πr
( By Aryabhatta)
The Value of π = 3.1416 or 22/7
(By Srinivas Ramanujam)

6. 2.AREAS OF SECTOR AND SEGMENT OF A CIRCLE
• Segment of a circle
A circular segment is a region of a circle which is “cut off”
from the rest of the circle by a secant or a chord.
• Sector of a Circle
A circle sector/ sector of a circle is defined as the region of
a circle enclosed by an arc and two radii. The smaller area is
called the minor sector and the larger area is called the major
sector.
• Angle of a Sector
The angle of a sector is that angle which is enclosed
between the two radii of the sector.

7.  Sector and segment:

8.  Length of an arc of a sector
The length of the arc of a sector can be found by using the
expression for the circumference of a circle and the angle of the
sector, using the following formula:
L= (θ/360°)×2πr
Where θ is the angle of sector and r is the radius of the circle.
 Area of a Sector of a Circle
Area of a sector is given by
(θ/360°)×π𝑟2
where ∠θ is the angle of this sector(minor sector in the following
case) and r is its radius
 Perimeter of the Sector: (θ/360°)×2πr+2r

9. Now let us take the case of the area of the segment APB of circle with
Centre O and radius r as shown in figure
Such that
Area of the segment APB = Area of the sector OAPB- Area of the triangle OAB
𝜃
3600 Xπ𝑟2
− 𝐴𝑟𝑒𝑎 𝑜𝑓 𝑡𝑟𝑖𝑎𝑛𝑔𝑙𝑒 𝑂𝐴𝐵
• Area of the major sector OAQB = π𝑟2
− Area of the minor sector OAPB
• Area of major segment AQB = π𝑟2
− Area of the minor segment APB

11. 3. Areas of combination of plane figures:
It’s a combination of geometric plane figures
some standard plane figures with shaded area marked:
To find the area of the shaded region in
 1. Shape A: find the difference between the area of the larger
circle and the area of the smaller circle
 2. Shape B: find the area of the square and then subtract the
area of the circle
 3. Shape C: Subtract the area of the rectangle from the area of
the circle
 4. Shape D: Difference between the area of the rectangle and
the triangle gives the area of the shaded region

12.  For Example:

13. References:
1.NCERT Text book
2.Google Sources
Thank you