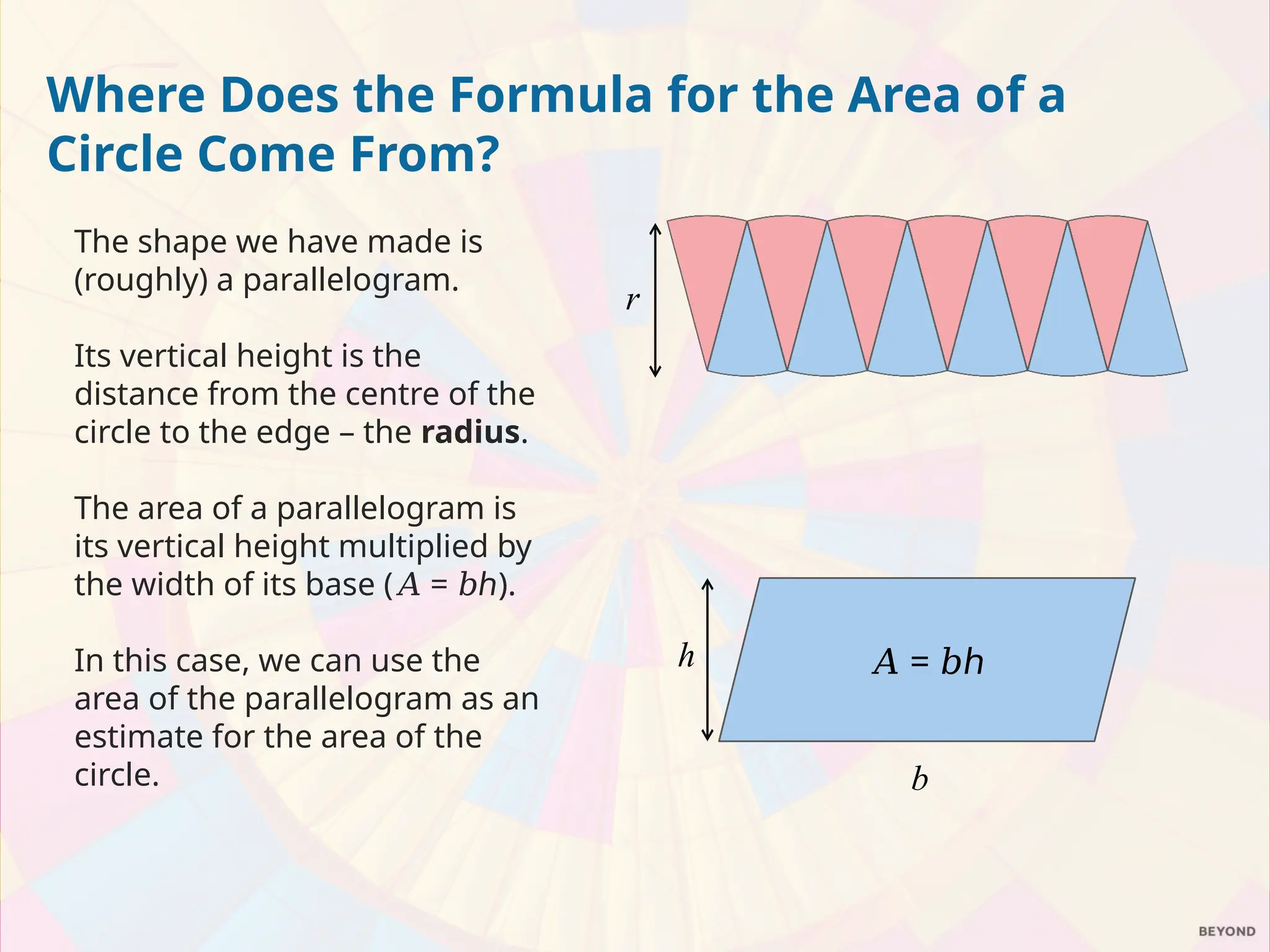
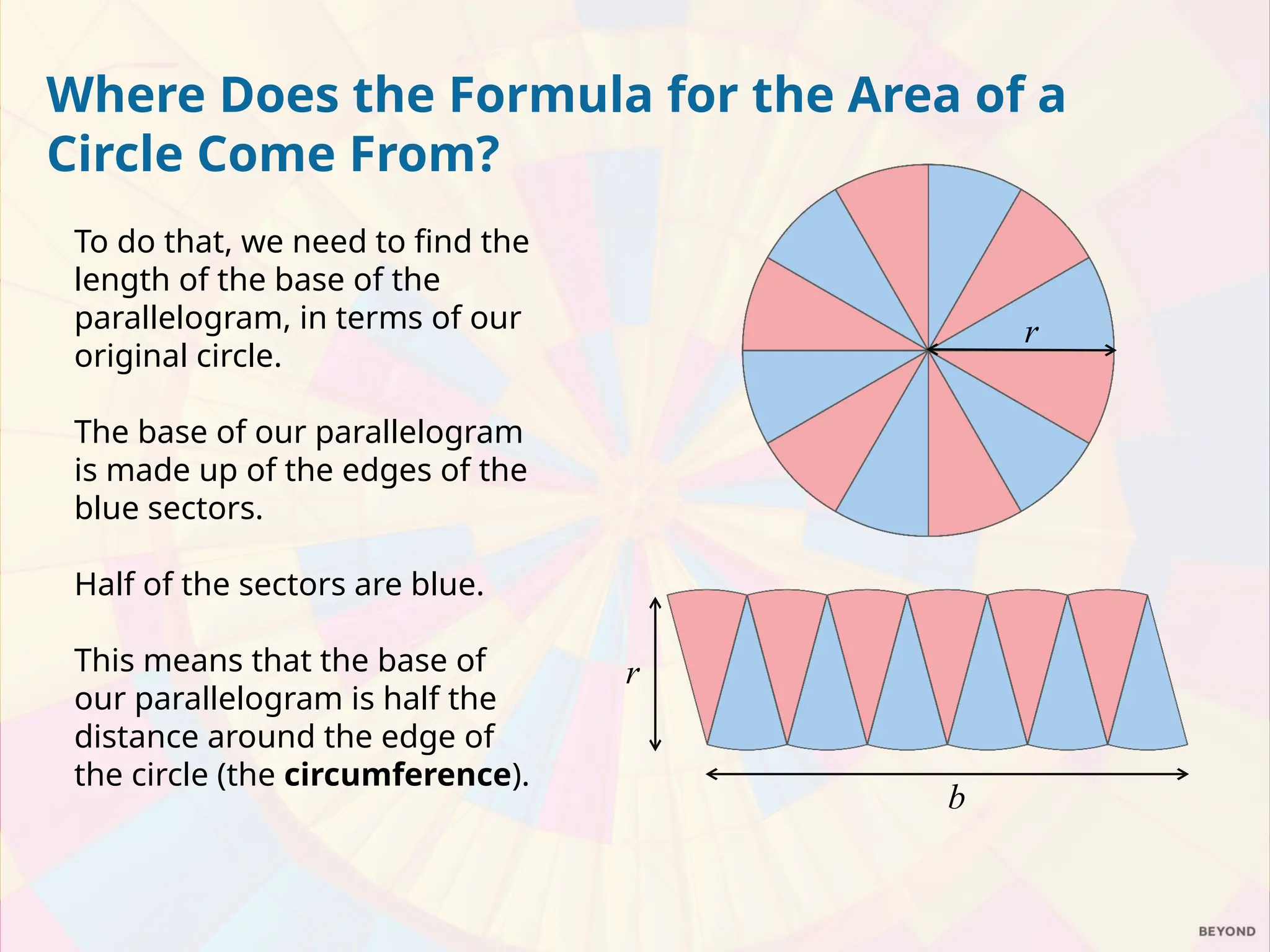
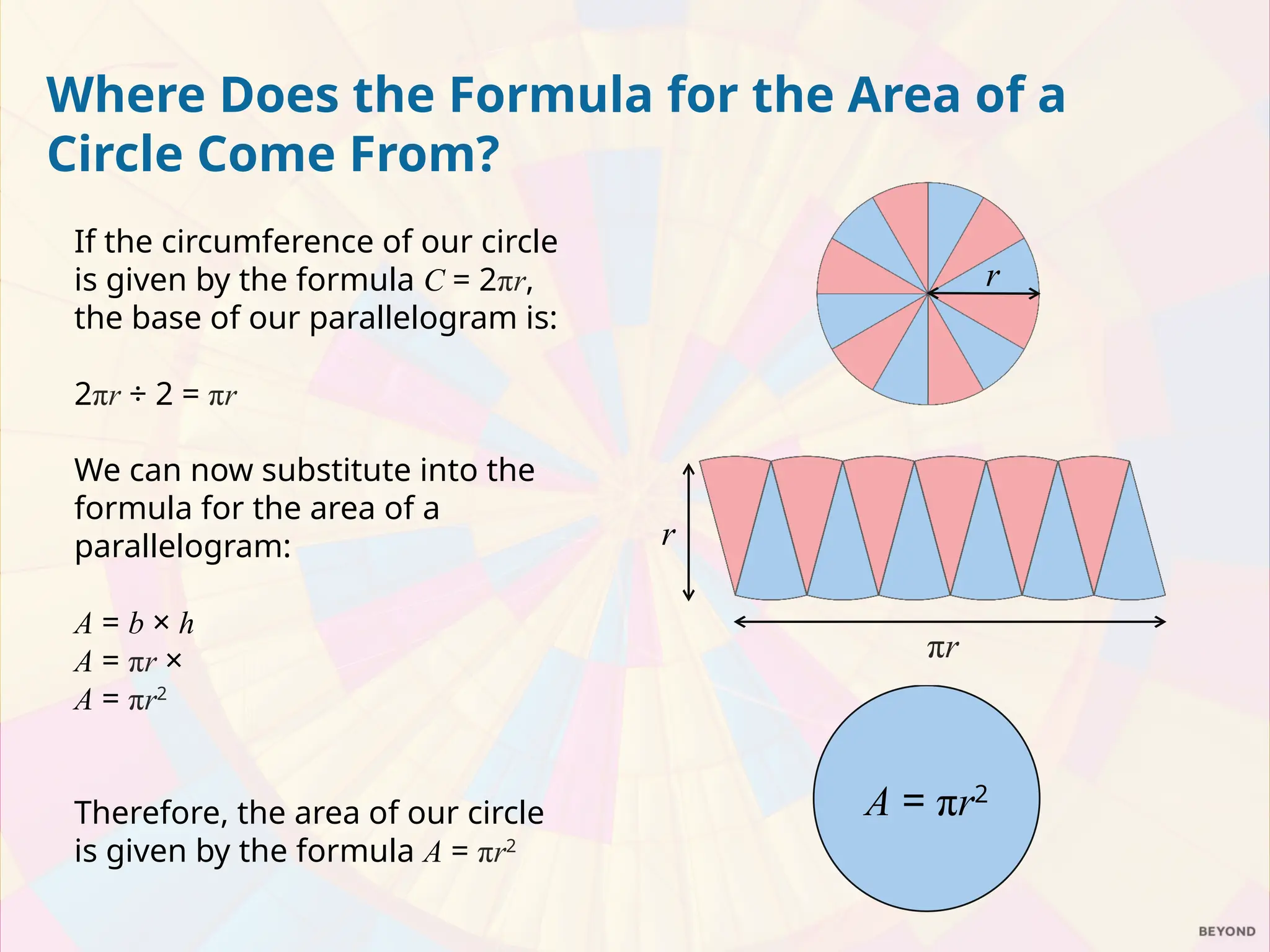
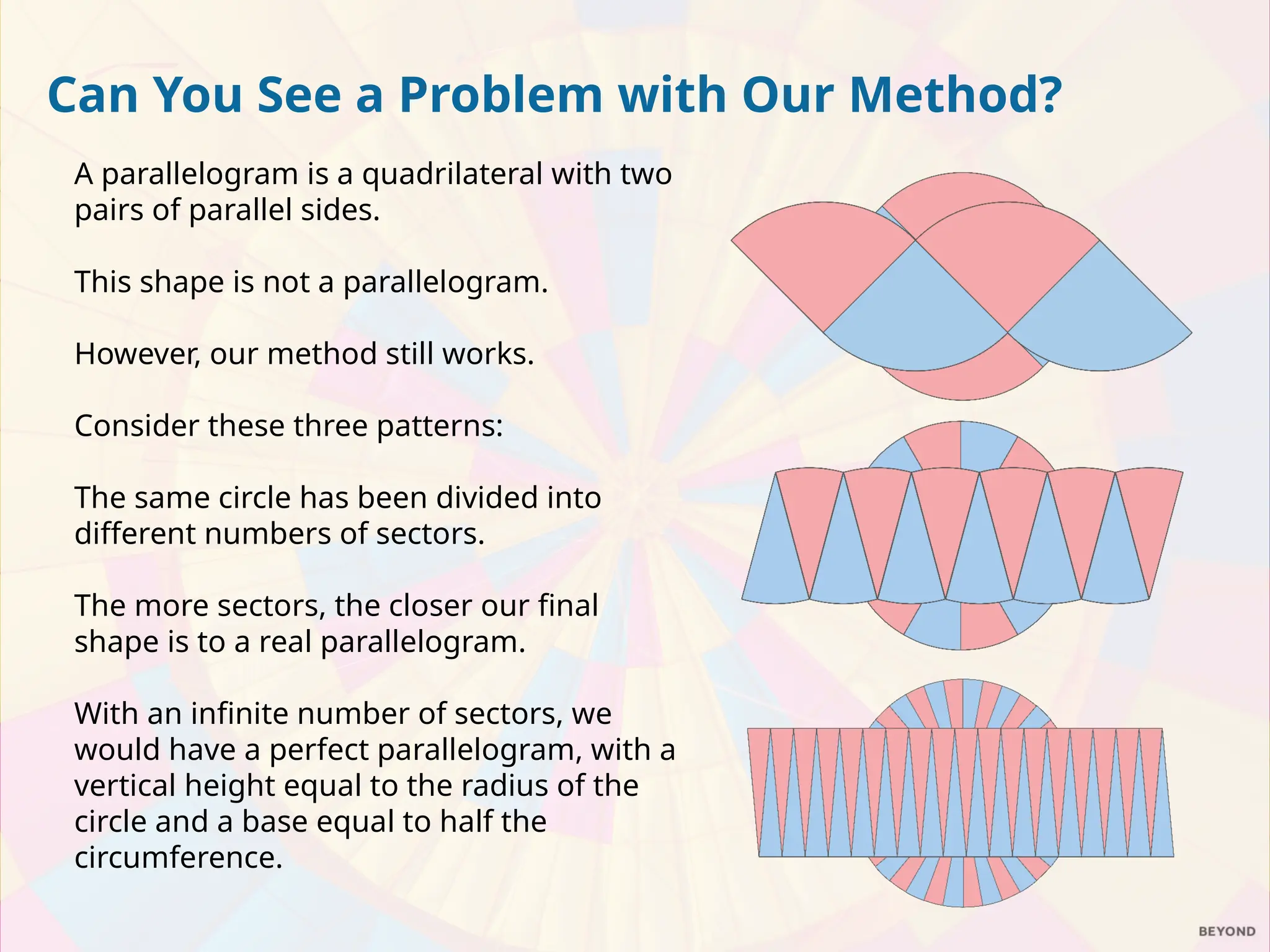
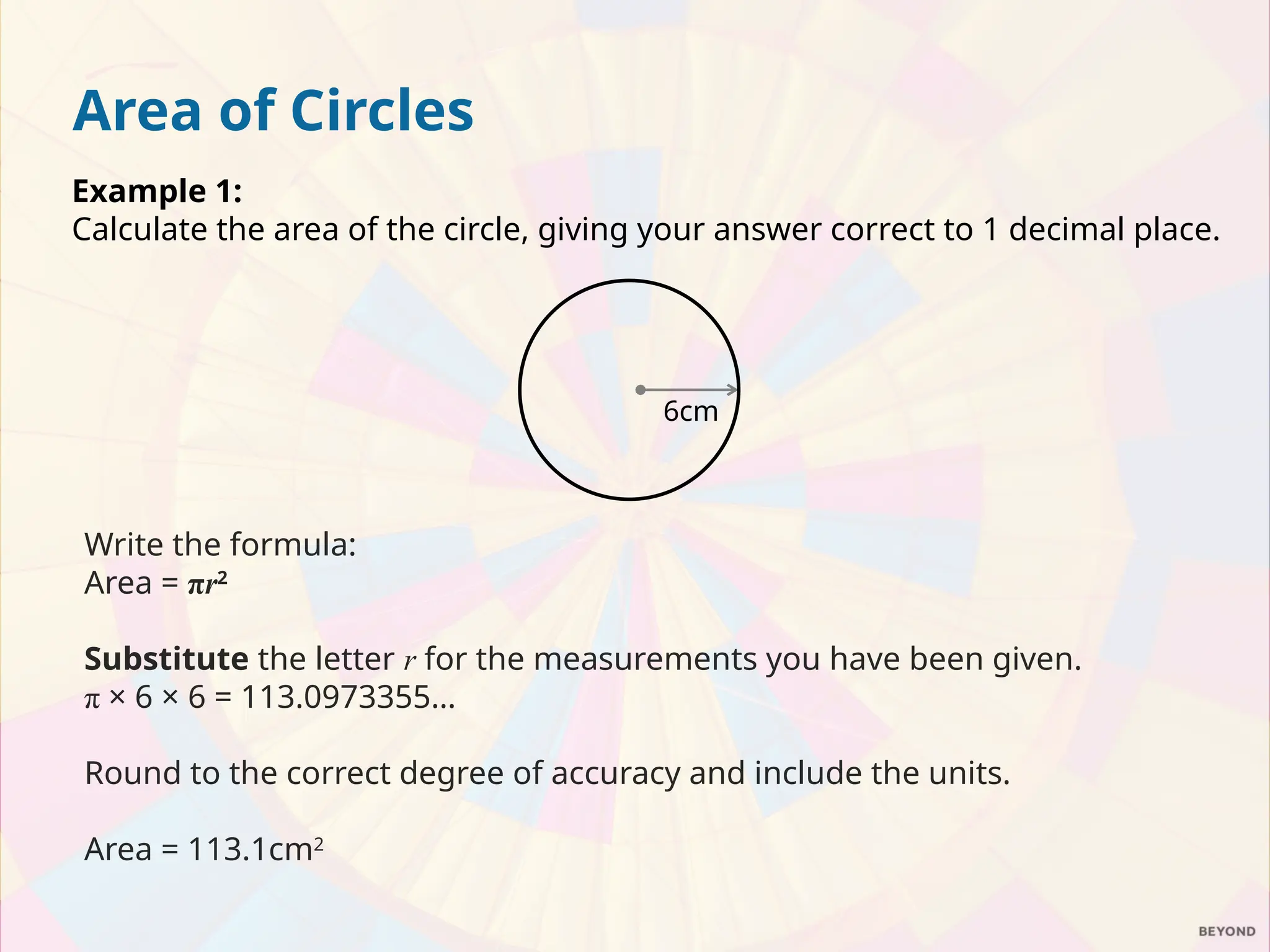
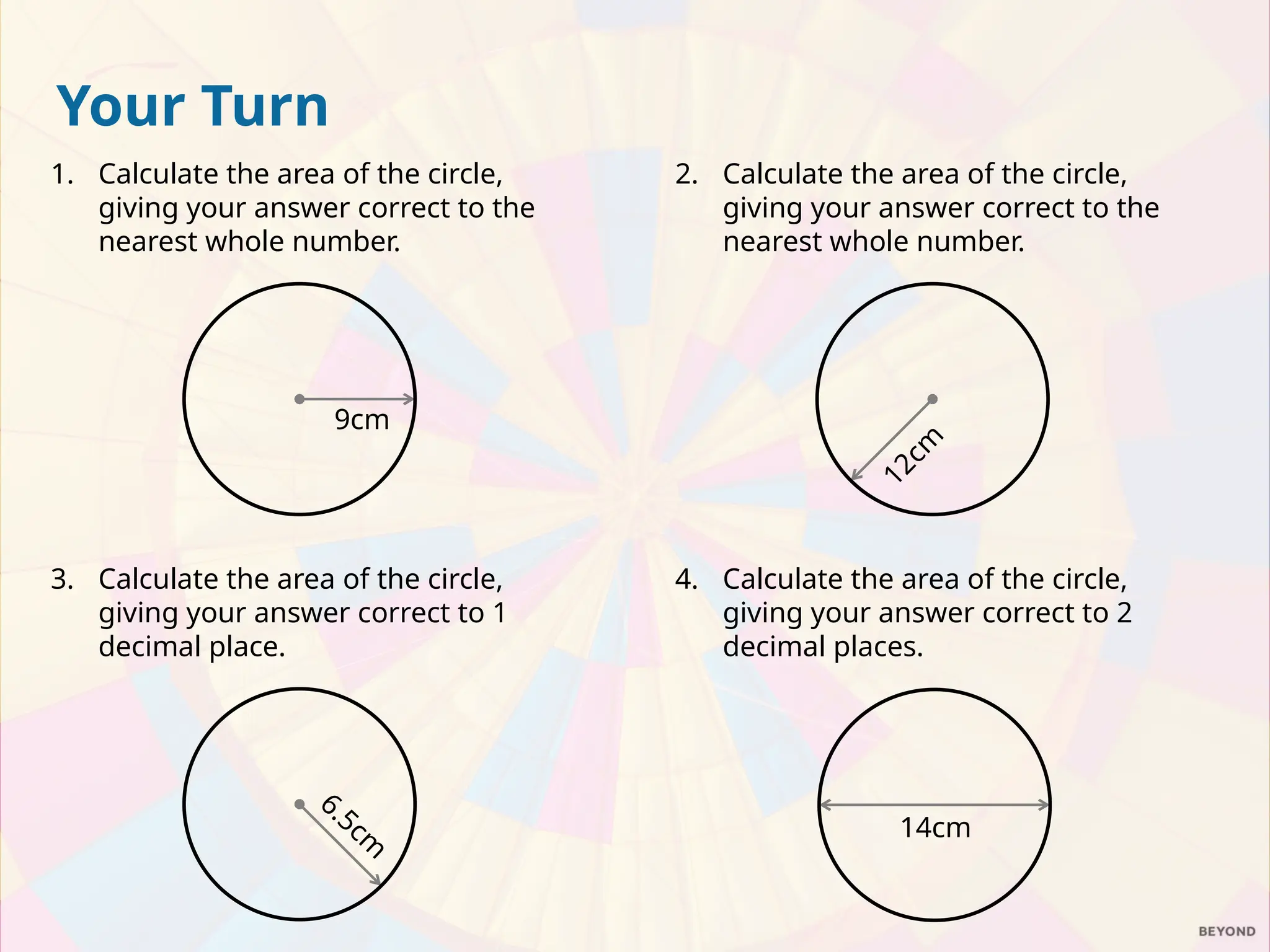
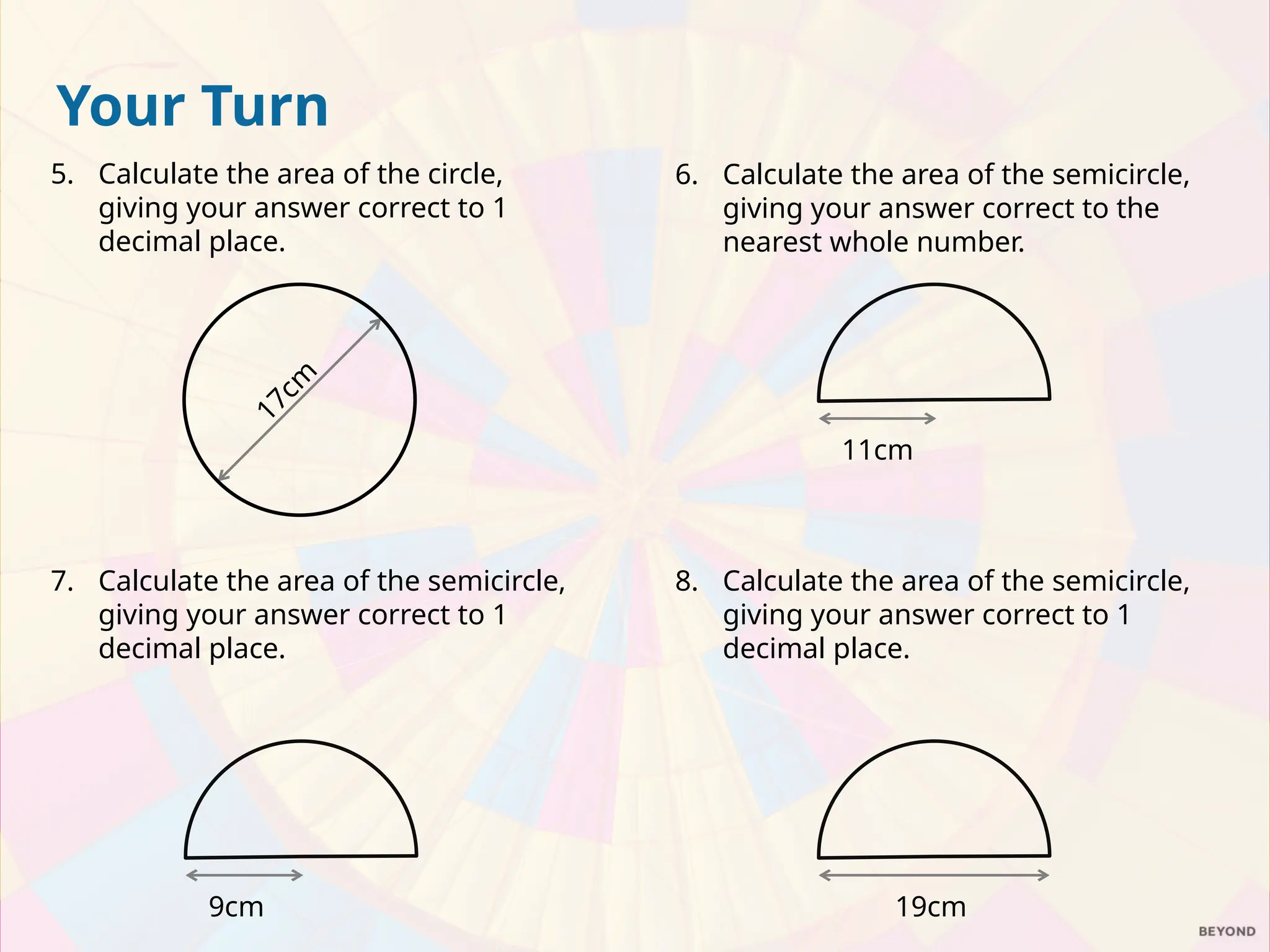
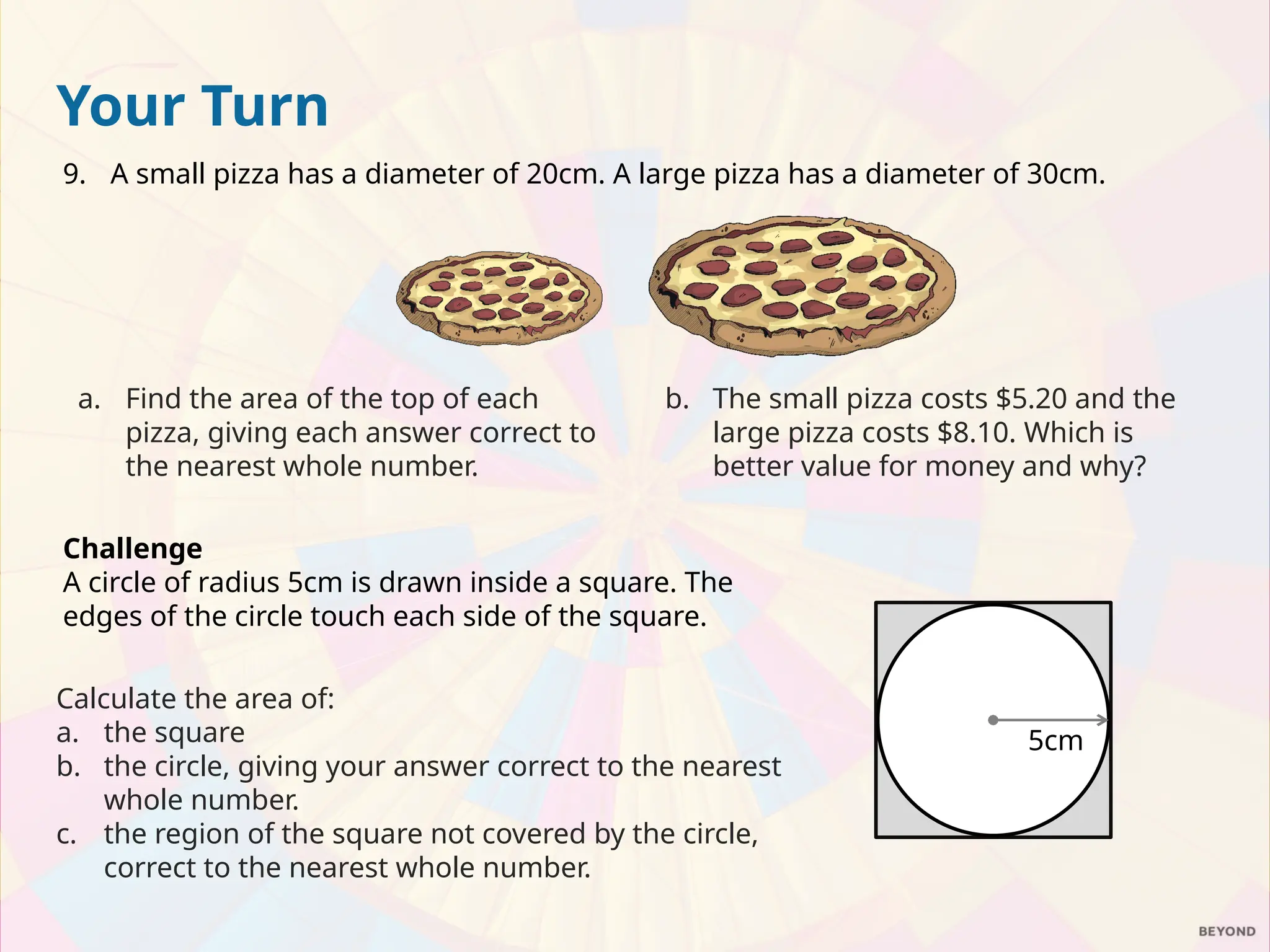
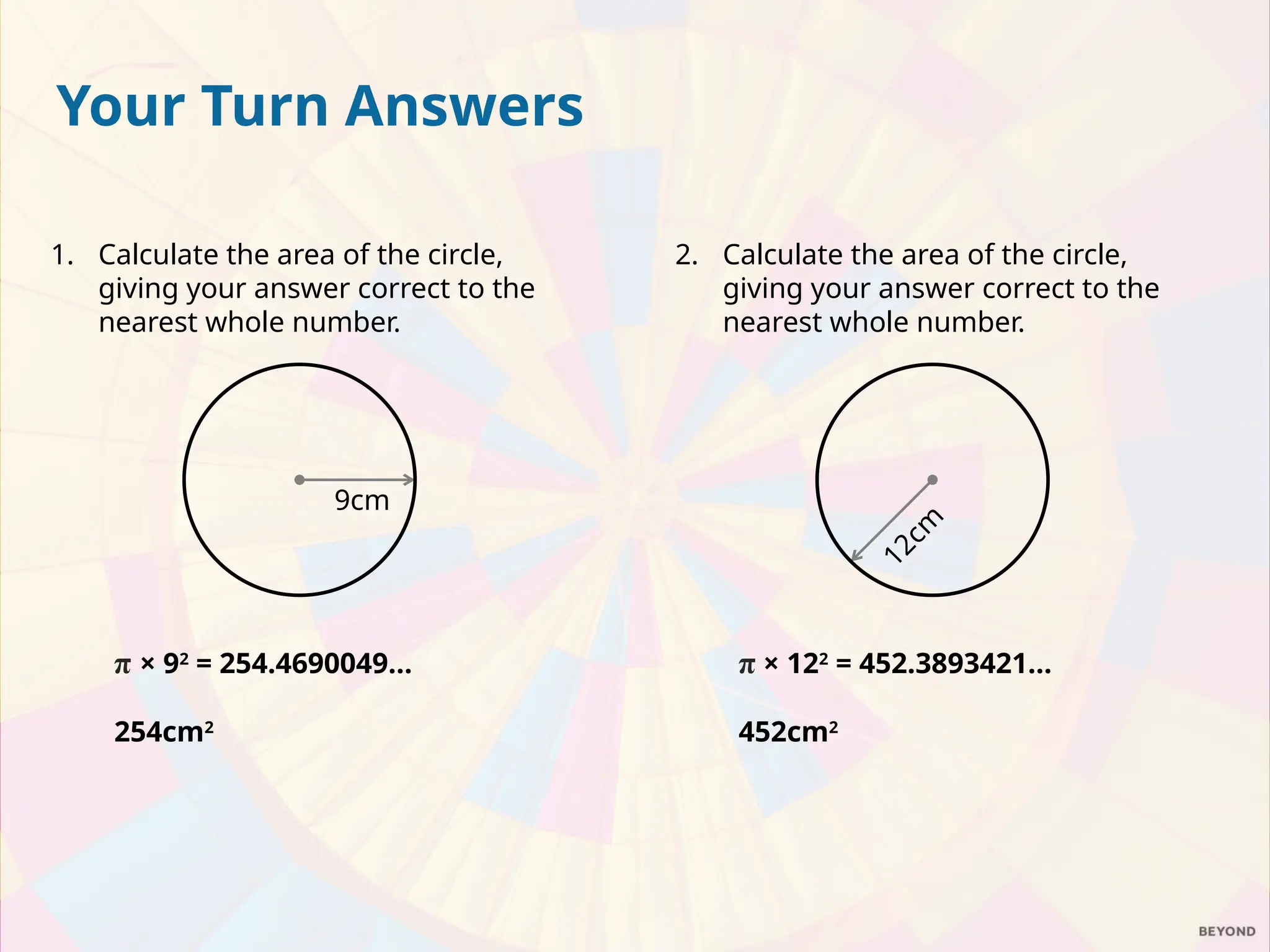
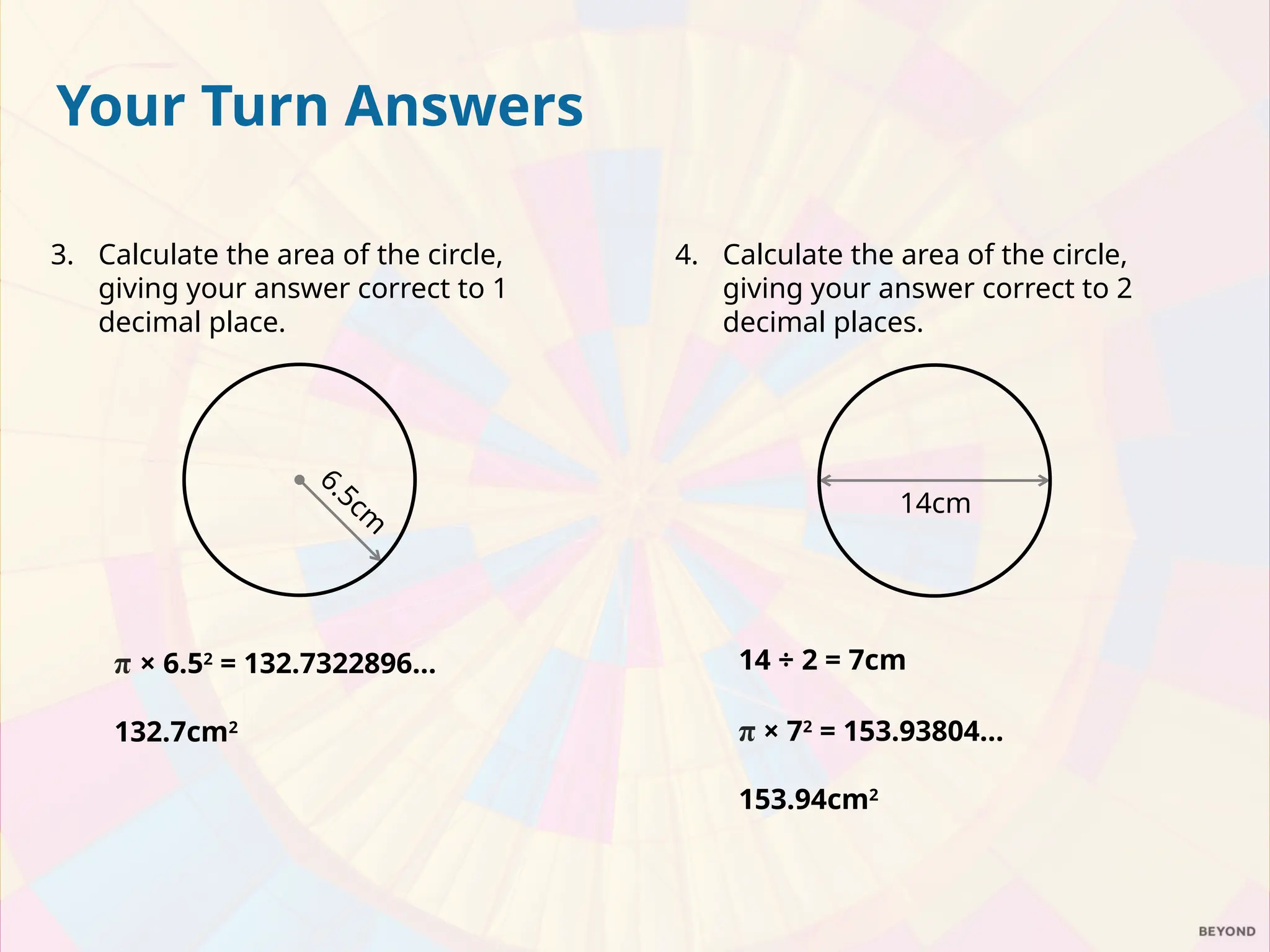
The document explains the relationship between the circumference, area, radius, and diameter of a circle, focusing on the derivation of the area formula A = πr². It demonstrates how the area can be estimated using the concept of rearranging sectors of a circle into a parallelogram, leading to practical examples of calculating areas for circles and semicircles. The document includes a series of exercises for calculating areas of various circles and compares the value of two pizzas based on their areas.

1. Circles, Areas
and Pi ()

2. • I can describe the relationship between circumference, area, radius
and diameter of a circle
• I can calculate the area of a circle using a formula
• Investigate the relationship between features of circles such as
circumference, area, radius and diameter
• Use formulas to solve problems involving area of circles
Learning Objectives
Success Criteria

3. Where Does the Formula for the Area of a
Circle Come From?
We know the area of a circle is given by the formula A = πr2
,
where r is the radius, but how can we show that this is
true?
A = πr2
Divide the circle into a number of equal
pieces (called sectors), from the centre.
Rearrange the sectors into this shape.

4. The shape we have made is
(roughly) a parallelogram.
Its vertical height is the
distance from the centre of the
circle to the edge – the radius.
The area of a parallelogram is
its vertical height multiplied by
the width of its base ( = ℎ).
𝐴 𝑏
In this case, we can use the
area of the parallelogram as an
estimate for the area of the
circle.
𝐴 = ℎ
𝑏
b
h
r
Where Does the Formula for the Area of a
Circle Come From?

5. To do that, we need to find the
length of the base of the
parallelogram, in terms of our
original circle.
The base of our parallelogram
is made up of the edges of the
blue sectors.
Half of the sectors are blue.
This means that the base of
our parallelogram is half the
distance around the edge of
the circle (the circumference).
r
r
b
Where Does the Formula for the Area of a
Circle Come From?

6. If the circumference of our circle
is given by the formula C = 2πr,
the base of our parallelogram is:
2πr ÷ 2 = πr
We can now substitute into the
formula for the area of a
parallelogram:
A = b × h
A = πr ×
A = πr2
Therefore, the area of our circle
is given by the formula A = πr2
r
r
πr
A = πr2
Where Does the Formula for the Area of a
Circle Come From?

7. Can You See a Problem with Our Method?
A parallelogram is a quadrilateral with two
pairs of parallel sides.
This shape is not a parallelogram.
However, our method still works.
Consider these three patterns:
The same circle has been divided into
different numbers of sectors.
The more sectors, the closer our final
shape is to a real parallelogram.
With an infinite number of sectors, we
would have a perfect parallelogram, with a
vertical height equal to the radius of the
circle and a base equal to half the
circumference.

8. Area of Circles
Example 1:
Calculate the area of the circle, giving your answer correct to 1 decimal place.
Write the formula:
Area = πr2
Substitute the letter r for the measurements you have been given.
π × 6 × 6 = 113.0973355…
Round to the correct degree of accuracy and include the units.
Area = 113.1cm2
6cm

9. Area of Circles
Example 2:
Calculate the area of the circle, giving
your answer correct to 1 decimal place.
This time, the diameter measurement has been given so the first step is to
halve it to find the radius.
10 ÷ 2 = 5cm
Write the formula:
Area = πr2
Substitute the letter r for the radius measurement you have just calculated.
π × 5 × 5 = 78.53981634…
Round to the correct degree of accuracy and include the units.
Area = 78.5cm2
10cm

10. Area of Circles
Example 3:
Calculate the area of the semicircle, giving your
answer correct to the nearest whole number.
This time, we have a semicircle. You can begin calculating the area of the
semicircle in the same way you would for a complete circle.
Write the formula:
Area = πr2
Substitute the letter r with the measurements you have been given.
π × 8 × 8 = 201.0619298…
Now, halve your answer (as you are calculating the area of a semicircle).
201.0619298… ÷ 2 = 100.5309649…
Round to the correct degree of accuracy and include the units.
Area = 101cm2
8cm

11. Your Turn
1. Calculate the area of the circle,
giving your answer correct to the
nearest whole number.
2. Calculate the area of the circle,
giving your answer correct to the
nearest whole number.
9cm
1
2
c
m
4. Calculate the area of the circle,
giving your answer correct to 2
decimal places.
14cm
3. Calculate the area of the circle,
giving your answer correct to 1
decimal place.
6.5cm

12. 8. Calculate the area of the semicircle,
giving your answer correct to 1
decimal place.
6. Calculate the area of the semicircle,
giving your answer correct to the
nearest whole number.
Your Turn
5. Calculate the area of the circle,
giving your answer correct to 1
decimal place.
1
7
c
m
19cm
7. Calculate the area of the semicircle,
giving your answer correct to 1
decimal place.
9cm
11cm

13. Your Turn
9. A small pizza has a diameter of 20cm. A large pizza has a diameter of 30cm.
a. Find the area of the top of each
pizza, giving each answer correct to
the nearest whole number.
b. The small pizza costs $5.20 and the
large pizza costs $8.10. Which is
better value for money and why?
Challenge
A circle of radius 5cm is drawn inside a square. The
edges of the circle touch each side of the square.
Calculate the area of:
a. the square
b. the circle, giving your answer correct to the nearest
whole number.
c. the region of the square not covered by the circle,
correct to the nearest whole number.
5cm

14. Your Turn Answers
1. Calculate the area of the circle,
giving your answer correct to the
nearest whole number.
π × 92
= 254.4690049…
254cm2
2. Calculate the area of the circle,
giving your answer correct to the
nearest whole number.
π × 122
= 452.3893421…
452cm2
9cm
1
2
c
m

15. 4. Calculate the area of the circle,
giving your answer correct to 2
decimal places.
14 ÷ 2 = 7cm
π × 72
= 153.93804…
153.94cm2
14cm
Your Turn Answers
3. Calculate the area of the circle,
giving your answer correct to 1
decimal place.
π × 6.52
= 132.7322896…
132.7cm2
6.5cm

16. 6. Calculate the area of the semicircle,
giving your answer correct to the
nearest whole number.
π × 112
= 380.1327111…
380.1327111… ÷ 2 = 190.0663555…
190cm2
11cm
Your Turn Answers
5. Calculate the area of the circle,
giving your answer correct to 1
decimal place.
17 ÷ 2 = 8.5cm
π × 8.52
= 226.9800692…
227.0cm2
1
7
c
m

17. 8. Calculate the area of the semicircle,
giving your answer correct to 1
decimal place.
19 ÷ 2 = 9.5cm
π × 9.52
= 283.528737…
283.528737 ÷ 2 = 141.7643685…
141.8cm2
19cm
Your Turn Answers
7. Calculate the area of the semicircle,
giving your answer correct to 1
decimal place.
π × 92
= 254.4690049…
254.4690049 ÷ 2 = 127.2345025…
127.2cm2
9cm

18. Your Turn Answers
9. A small pizza has a diameter of 20cm. A large pizza has a diameter of 30cm.
a. Find the area of the top of each
pizza, giving each answer correct to
the nearest whole number.
Small pizza
20 ÷ 2 = 10cm
π × 102
= 314.1592654…
314cm2
Large pizza
30 ÷ 2 = 15cm
π × 152
= 706.8583471…
707cm2
b. The small pizza costs $5.20 and the
large pizza costs $8.10. Which is
better value for money and why?
Small pizza: 5.20 ÷ 314.1592654 =
$0.01655211408 per cm2
Large pizza: 8.10 ÷ 706.8583471 =
$0.0114591559 per cm2
The large pizza presents better
value for money because it is
cheaper per cm2
.

19. Your Turn Answers
Challenge
A circle of radius 5cm is drawn inside a square. The
edges of the circle touch each side of the square.
Calculate the area of:
a. the square
5 × 2 = 10cm
10 × 10 = 100cm2
b. the circle, giving your answer correct to the nearest whole number.
π × 52
= 78.53981634…
79cm2
c. the region of the square not covered by the circle, correct to the nearest whole
number.
100 – 78.53981634… = 21.46018366…
21cm2
5cm