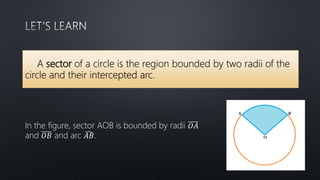
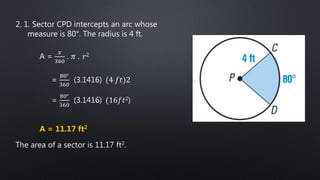
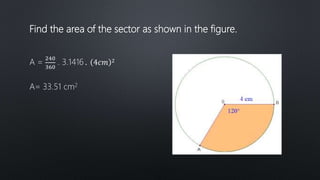
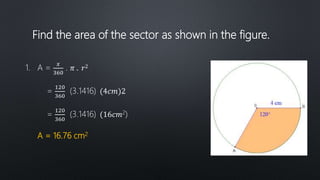
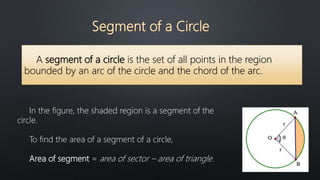
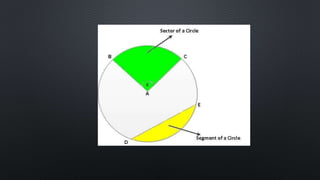
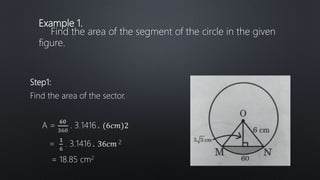
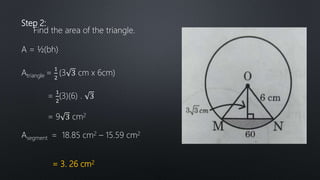
The document discusses finding the area of sectors and segments of circles. It defines a sector as the region bounded by two radii and their intercepted arc, and provides a formula to calculate the area of a sector based on the radius and arc measure. A segment is defined as the region bounded by an arc and its chord. To find the area of a segment, you calculate the area of the sector using the formula, then subtract the area of the triangle formed by the arc and chord. Two examples demonstrate using these formulas to solve for sector and segment areas.

2. A sector of a circle is the region bounded by two radii of the
circle and their intercepted arc.
In the figure, sector AOB is bounded by radii 𝑂𝐴
and 𝑂𝐵 and arc 𝐴𝐵.

3. Theorem 1.
The ratio of the area A of a sector of a circle to the area of a
circle is equal to the ratio of the measures of the intercepted arc to
360.
In the figure,
𝐴
𝜋𝑟2 =
𝑚𝐴𝐵
360
or A =
𝑚𝐴𝐵
360
. 𝜋𝑟2
Theorem 2. Area of a Sector Theorem
If a sector has radius r and its arc has measure x, then the
are A is A =
𝑥
360
. 𝜋 . 𝑟2

4. Illustrative Examples:
A. Find the area of the sector as shown in the
figure.
Solution:
1. Sector KLM intercepts an arc whose
measure is 120°. The radius is 9.
A =
𝑥
360
. 𝜋 . 𝑟2
=
120
360
. (3.1416) . (9)2
A = 84.82
The area of the sector 84.82

5. 2. 1. Sector CPD intercepts an arc whose
measure is 80°. The radius is 4 ft.
A =
𝑥
360
. 𝜋 . 𝑟2
=
80°
360
(3.1416) (4 𝑓𝑡)2
=
80°
360
(3.1416) (16𝑓𝑡2)
A = 11.17 ft2
The area of a sector is 11.17 ft2.

6. Find the area of the sector as shown in the figure.
A =
240
360
. 3.1416 . 4𝑐𝑚 2
A= 33.51 cm2

7. Find the area of the sector as shown in the figure.
1. A =
𝑥
360
. 𝜋 . 𝑟2
=
120
360
(3.1416) (4𝑐𝑚)2
=
120
360
(3.1416) (16𝑐𝑚2)
A = 16.76 cm2

8. A segment of a circle is the set of all points in the region
bounded by an arc of the circle and the chord of the arc.
In the figure, the shaded region is a segment of the
circle.
To find the area of a segment of a circle,
Area of segment = area of sector – area of triangle.

10. Example 1.
Find the area of the segment of the circle in the given
figure.
Step1:
Find the area of the sector.
=
= 18.85 cm2

11. Step 2:
Find the area of the triangle.
A = ½(bh)
Atriangle =
1
2
(3 3 cm x 6cm)
=
1
2
(3)(6) . 3
= 9 3 cm2
Asegment = 18.85 cm2 – 15.59 cm2
= 3. 26 cm2