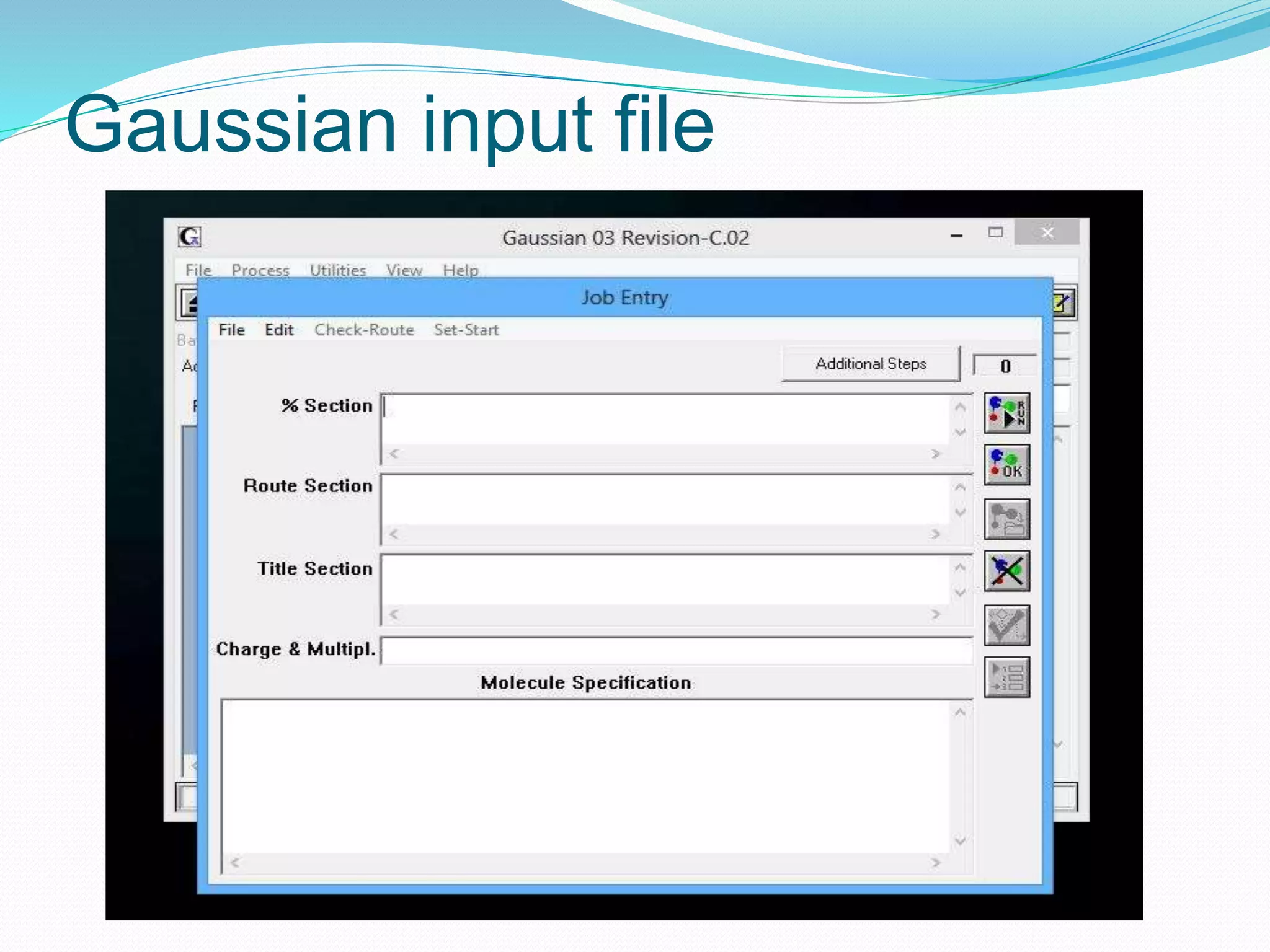
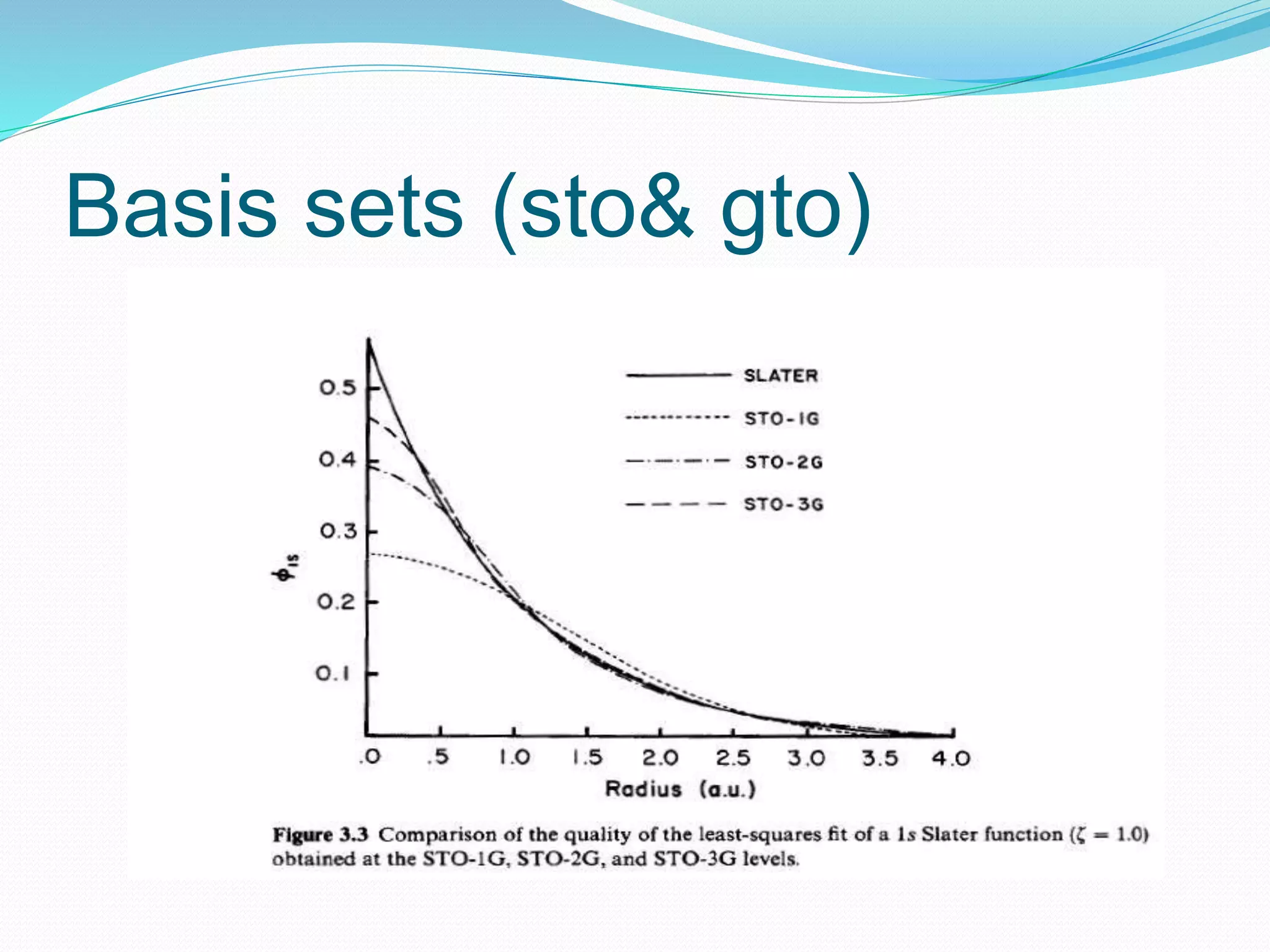
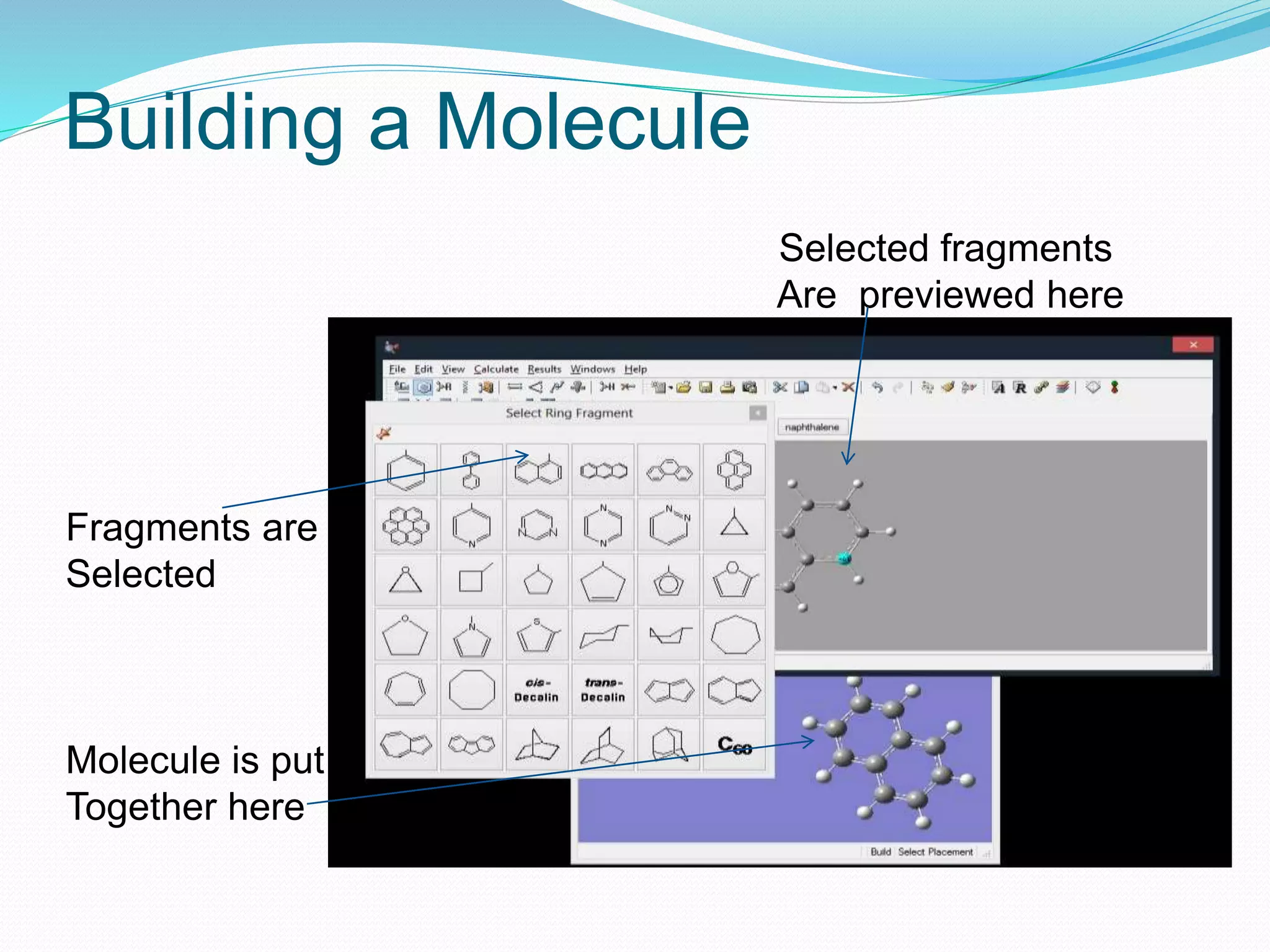
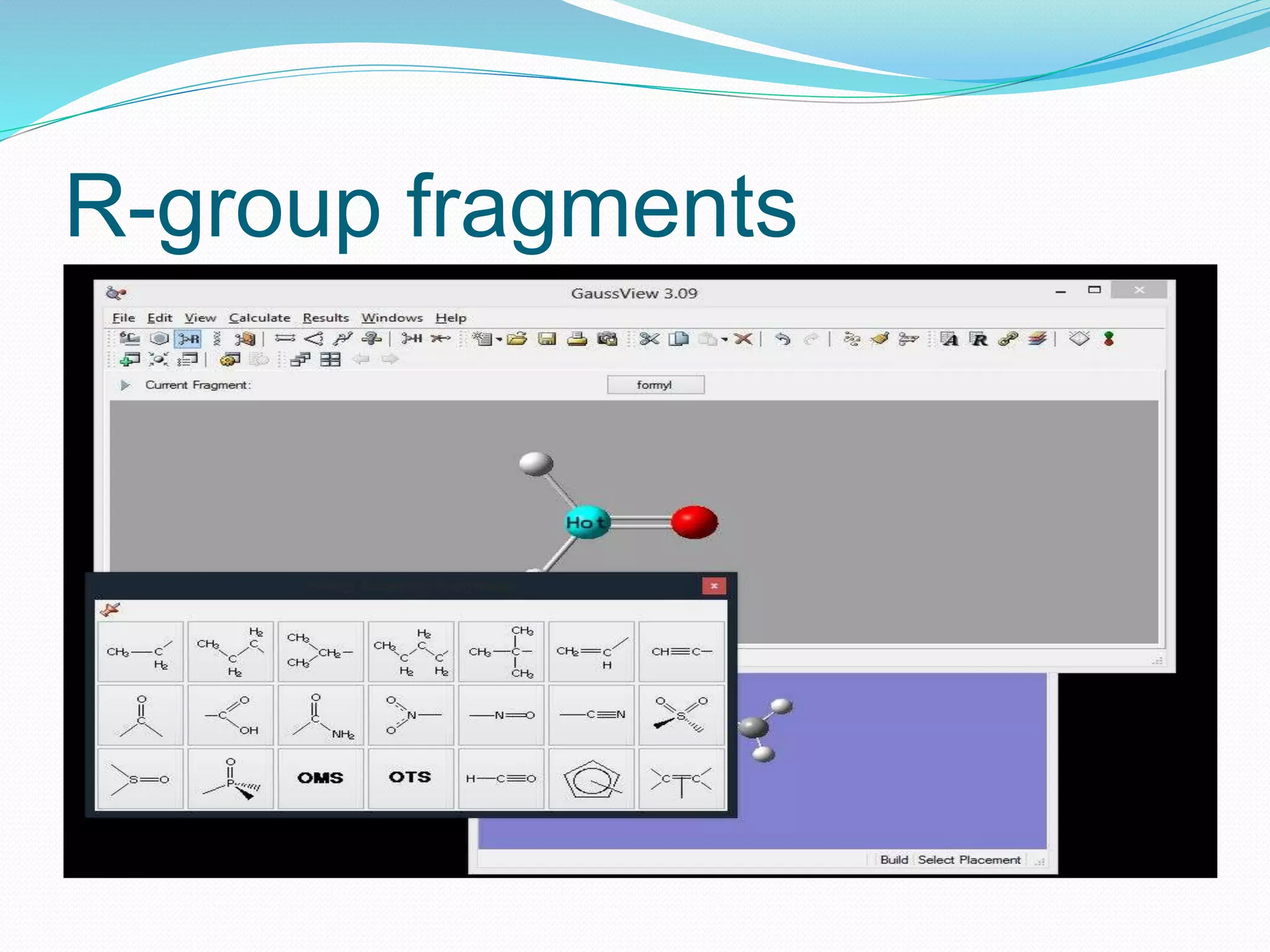
Gaussian is capable of performing several quantum chemical calculations including molecular energies, geometry optimization, vibrational frequencies, NMR properties, potential energy surfaces, and reaction pathways. It takes a Gaussian input file specifying the calculation type, theory, basis set, coordinates, etc. Common calculation types include single point energy, geometry optimization, and vibrational frequency. The output file provides optimized geometry, frequencies, energies, and other molecular properties.

2. Gaussian is capable of perdecting
many properties of the Atoms ,
molecules
 Molecular Energies
 Geometry optimisation
 Viberational frequencies
 NMR Properties
 Potential energy surface
 Reaction pathways

3. How to Create Input File

4. Gaussian input file

5. Eg : Water optimization
%mem=32mb System resources
#p hf/6-31g opt calculation type, method
basis set
hf/6-31g optimization of water titile
0 1 charge & multiplicity
O1 -0.464 0.177 0.0
H2 -0.464 1.137 0.0 molecular specification
H3 0.441 -0.143 0.0 z matrix or cartesian c.

6. Commands for Resource
Management(link 0)
%mem=n set the amount of dynamic meomory(n)
default is 32 mb
%chk=file location and name of checkpoint file
%nproc=n set the number of processors, n to use

7. Example of Route section
#n optfreqb3lyp/6-31g*
Where #n = normal print output, #p = max print output,
#t=min print output
Opt = geometry optimization
Freq = viberational frequencies
B3lyp = DFT(method)
6-31g* = Basis set
# HF/6-31g*Pop=Reg
#p B3LYP/cc-pvdz opt

8. Spin Multiplicity
Multiplicity = n + 1
where n = #no of unpaired electron

9. Calculation types
 Single point energy
 Geometry Optimization
 Viberational Frequency

10. Single Point Energy
 Keyword Sp
 It simply calculates Energy ,wavefunction and other
requested properties at single fixed geometry.
 It is also frequently carried out after a geometry
optimization.
 If no keyword present in route section By default
calculation leads to HF/STO-3G Sp
 Information get out of this calculation
single point energy(hartree), orbital Symmetries,Mullkien
atomic charges,Dipole Moments

11. Geometry Optimization
 Keyword : Opt
 It is a procedure that attempts to find the configuration of
Minimum Energy of the Molecule.
 It also calculate the Force on each atom by evaluating
gradient(first derivative) of energy with respect to atomic
postion
 It stops when a stationary point found(point where force
on each atom is zero)
 Information get out of this calculation
Atomic coordinates of optimized molecule
Optimized Parameters: atomic distances and angles
HOMO/LUMO eigenvalues (Hartrees)

12. Viberational Frequency
 Keyword : Freq
 It calculates the viberation of molecule
 Molecule Frequencies depend on the second derivative
of Energy with respect to nuclear Position(Hessian
matrix)
Information get out of this calculation
Single Point energy
Harmonic frequnecies (wavenumbers)
Reduced masses (amu)
Force constants
IR intensities
Raman intensities (not default)

13. Theoretical model
 Ab initio Methods :
HF,MP2,CCSD,QCISD
 Semi-emperical Method
AM1,MNDO,PM3
 Density functional theory
B3LYP,VWN,PW91

14. Ab initio Methods
 It is based on theoretical Principle and doesnot use
any experimental data other than constants.
 Using this method : calculation takes reasonably
long time.
 Example : Hf : Hartree fock
MPn :Moller Pesset Peterbation Theory
while Mp2, Mp4 most commonly used
Couple cluster(cc method)
CCSD,QCISD

15. Semi-emperical Methods
 Semi emperical methods are based hartree fock
formalism.
 It parmetrize or neglect the integrals based on
experimental data
 It can be applied to large molecules and give
accurate results
Methods : MNDO : modified neglect of diatomic
overlap
AM1 : austin model 1
PM3 : parmeterized model number 3

16. Density functional theory
 Dft methods are becoming more popular because
results obtained are comparable to ab intio methods
Dft differs from methods based on Hf calculation in
the way that it uses Electron density to compare
energy instead of wave function
eg: B3LYP : Becke3-parameter, Lee-Yang-Parr
VWN : Vosko Wilk Nusair Functional
PW91 : Perdew-Wang

17. Population analysis
 This keyword control the printing of molecular orbitals
and several types of population analysis and atomic
charges.
 Population are done once for Sp energy calculation and
at the first and last step of geometry optimisation.
 Keywords
Pop=minimal
Pop=none
Pop=full
Pop=regular

18. Types of basis sets
 Minimal basis sets
Sets which uses only one function for each atomic
orbital STO-nG means that n GTO are used to
describe one STO and only one STO is used to
describe an AO(Single Zeta).
Usually n<3 gives poor result so STO-3g is called
the minimal basis set

19. Basis sets (sto& gto)

20. Split-Valence
 A split valence basis uses one basis function for core
Atomic orbitals (1s²) and larger basis for valance
Atomic orbital
 Double-zeta Function
Two Basis function for each atomic orbital
 Triple-zeta Function
Three Basis function for each atomic orbital
and Qz,5z,6z,… so on Split valence
Eg: CH4 for C atom (1s²,2s²,2p²)

21. Eg: CH4 with split valence
double zeta basis
 C atom (1s²,2s²,2p²)
 With double zeta basis function
 C atom (1s²,2s’²,2s², 2px’2px,2py’2py,2pz’2pz)
 We get value 9
 Similarly for H atom (1s¹)
 With double zeta basis function(1s¹’1s¹)
 So 4*2=8
 Total value is 9+8= 17

22. Pople basis sets
 3-21G
3 Gtos for inner shell(core) , 2 Gtos for inner
valence , 1 Gto for outer valence
 6-31G
 6-311G

23. Polarization function
 *type (6-31G*)
 D type function added other than hydrogen atom and
f type function added on the transition metals
 **type (6-31G**)
 P type function added on hydrogen atom and d type
function added on all other atom, f type function
added on transition metals

24. Diffused function
 To provide more accurate description of anion or
neutral molecules
 + : diffuse function added on to atoms other than
hydrogen
 ++: diffuse function added on to all atoms
 6-31G+
 6-31G++

25. Dunning basis sets
 Correlation consistent
 Dunning created basis sets that can optimized using
correlated (CISD) wavefunction
various types
cc-pVXZ
cc= indicates that it is a correlation-consistent basis
pV= indicates that it is a polarized valence basis
xz = indicates the zeta number (x = D for Double , T for
triple , Q for quadruple , 5,6,7)
The prefix aug- can be used to add diffuse function
eg : aug-cc-pVTZ , aug-cc-VDZ

26. Z matrix
Hydrogenperoxide(h2o2)
 Z Matrix
0 1
O1
O2 O1 r2
H3 O1 r3 O2 a3
H4 O2 r3 O1 a3 H3 d4
(Blank line)
r2 = 1.3963
r3 = 1.011
a3 = 101.1196
d4 = 124.993

27. Building with Gauss View
 Instead of typing all the coordinates, theory, basis
set, etc., we can use GaussView.
 The calculation is specified by pointing and clicking
to build the molecule, and using pull-down menus to
select the calculation type, level of theory and basis
set.
 GaussView generates the Gaussian input file, and
can run Gaussian without ever returning to the Unix
prompt.
 GaussView can also be used to read Gaussian
output files and visualize the results

28. Gauss view
Builder viewer

29. Building a Molecule
Selected fragments
Are previewed here
Fragments are
Selected
Molecule is put
Together here

30. Biological fragments

31. R-group fragments

32. Method & Basis sets

33. Gaussian output file water

34. Gaussian output file water

35. Gaussian output file water

36. Gaussian output file water
 (…..)
1 2
3
A1 A1
B2
Frequencies -- 1737.0306 3988.3491
4145.2817
Red. masses -- 1.0915 1.0370
1.0887
Frc consts -- 1.9404 9.7193
11.0225

37. Gaussian output file water
………
This molecule is an asymmetric top.
Rotational symmetry number 2.
Rotational temperatures (Kelvin) 47.48924 19.51815 13.83283
Rotational constants (GHZ): 989.51639 406.69263 288.22978
Zero-point vibrational energy 59039.7 (Joules/Mol)14.11082
(Kcal/Mol)
Vibrational temperatures: 2499.20 5738.34 5964.13 (Kelvin)
Zero-point correction= 0.022487 (Hartree/Particle)
Thermal correction to Energy= 0.025321
Thermal correction to Enthalpy= 0.026266
Thermal correction to Gibbs Free Energy= 0.004914

38. Gaussian output file
 Geometry optimization and frequency calculation
 In the output file (log file)

39. Gaussian output file
 When the number in value reaches the number in
threshold then the optimization is completed.