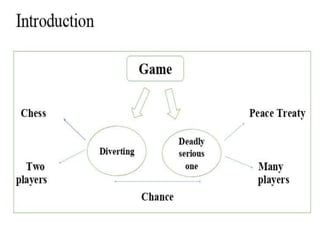
The document discusses game theory, focusing on non-zero-sum games where players' interests can overlap, emphasizing the complexity of cooperation without communication, exemplified by the prisoner's dilemma. It explores cooperative games where players may achieve better outcomes through coordination, highlighting the concept of Pareto optimal points and the challenges in identifying fair solutions. The text transitions to bargaining games, introducing Nash's solution as a guaranteed Pareto optimal point within the bargaining region.

1. Chapter: 5
Game Theory
Fatima zaheer
national defence university

3. Elements
• Two or more players
• One or more moves
• Rules of the game
Game:
scissors, paper, and stone
• Revealing their choices at the same time
• Outcome is immediate and understandable

5. Non-zero-sum games
• The gains of one player differ from the losses of the
other
• Players' interests overlap entirely
• No accepted solution.
• There is no single optimal strategy that is preferable
to all others, nor is there a predictable outcome.
• It is different from zero sum games in which the
winner receives the entire amount of the payoff
which is contributed by the loser.

6. Non-zero-sum games
• Cooperation may be achieved whether or not
there is direct communication.
• No communication, information is necessarily
imperfect
• Communication, there may be bargaining

7. The Prisoner’s Dilemma
• For example: Two men suspected of committing a bank
robbery together and are arrested by the police. They
are placed in separate cells, so that they cannot
communicate.
• Each suspect may either confess or remain silent. They
know the consequences of their actions.
Player B
PlayerA

8. COOPERATIVE GAMES
• Communication between the players in a game is impossible.
• They had no opportunity to coordinate their strategies and realize
together what neither can obtain on his own.
• Lets now give them that opportunity.
• Clash Of Wills
• Intuitively the fair solution was for the players to toss a coin and go
skiing together on heads and to the festival on tails (But they could not
coordinate their strategies)
• First, suppose Col and Row cannot communicate but each decides
separately to flip a coin and play his first strategy on heads and his
second on tails.

10. COOPERATIVE GAMES
• Horizontal axis is Row's scale and whose vertical axis is Col's scale.
• Then when x = 0, their coordinated strategy yields the point (2, 1).
• When x = 1, it yields the point (1,2), and when x falls between
these values, it yields a point on the line joining (2, 1) and (1, 2).
• It can be shown that Row and Col can achieve no utility points
better than the points on this line. Thus each of these points is
Pareto optimal.
• Yet, of course, those toward the (2, 1) end of the line are better
for Row and those toward the (1, 2) end are better for Col. The
problem for game theory, then, is to determine which point or
points on this line to recommend as the solution for the game

11. COOPERATIVE GAMES
• Furthermore, by playing coordinated strategies the players
can guarantee that they avoid outcomes that are worse for
both of them.
• The set of outcomes players can achieve by playing either
coordinated or individual strategies the achievable set.
• Limit our attention to the Pareto optimal members of the
achievable set.
• If only one does better, he does so at no cost to the
other-not even in psychological terms.
• Some game theorists think that all strategies that
produce Pareto optimal outcomes in a cooperative
game should count as solutions to that game.

12. COOPERATIVE GAMES
• But that does not distinguish the apparently "fair" outcome
(3/2, 3/2) of our recent game from the "biased" ones (2, 1) or
(1, 2), nor in a cooperative version of the prisoner's dilemma
would it distinguish ( — 1, — 25) and (— 25, — 1) from the
"cooperative" outcome ( — 2, — 2), since all three outcomes
are Pareto optimal.
• Thus the situation will quickly degenerate into a competitive
game in which the players vie for Pareto optimal outcomes
favourable to themselves.
• One way to deal with this is to have the players bargain for
Pareto optimal outcomes. This leads us to bargaining games.

13. BARGAINING GAMES
• The set of achievable outcomes will be called the bargaining
region of the game.
• We will assume that the region contains at least two Pareto
optimal points for otherwise there would be nothing to contest.
• The region contains a non Pareto optimal point, called the failure
point of the game, which marks the payoffs to the players in case
they fail to cooperate.
• The problem for the game theorist is to specify a point within the
bargaining region that would be selected by rational bargainers.
Let us call such a point the negotiation point of the game.
• We will examine first a solution proposed by John Nash.

15. Why Should We Count This Point As A
Solution?
• First, the Nash point is certain to be Pareto optimal.
• For if a point is not Pareto optimal, one or both of
the utility gains associated with it will be smaller
than those associated with some other point and
none of the gains will be larger than those associated
with any other point.
• Thus its associated product will not be maximal and
it cannot be a Nash point.
• Second, there will be only one Nash point