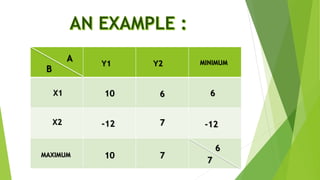
The document discusses game theory, its history, key concepts, and applications in various fields such as economics, psychology, and military strategy. It explains important elements like players, strategies, payoffs, and the concept of Nash equilibrium, illustrating these principles with examples including the prisoner's dilemma and penny matching game. The theory, established by pioneers like John von Neumann and John Nash, provides mathematical insights into competitive decision-making scenarios.

1. QUANTITATIVE ANALYSIS FOR DECISION MAKING
(QUANTITATIVE MANAGEMENT PROJECT)

2.  WHAT IS GAME THEORY?
 HISTORY OF GAME THEORY
 APPLICATIONS OF GAME THEORY
 KEY ELEMENTS OF A GAME
 TYPES OF GAME
 NASH EQUILIBRIUM (NE)
 PURE STRATEGIES AND MIXED STRATEGIES
 2-PLAYERS ZERO-SUM GAMES
 PRISONER’S DILEMMA

3.  THE BRANCH OF MATHEMATICS CONCERNED WITH THE ANALYSIS
OF STRATEGIES FOR DEALING WITH COMPETITIVE SITUATIONS,
WHERE THE OUTCOME OF A PARTICIPANT’S CHOICE OF ACTION
DEPENDS CRITICALLY ON THE ACTIONS OF OTHER PARTICIPANTS.
 GAME THEORY HAS BEEN APPLIED TO CONTEXTS IN WAR,
BUSINESS AND BIOLOGY.
 THE MATHEMATICS OF HUMAN INTERACTIONS.

4.  THE MATHEMATICAL THEORY OF GAMES WAS INVENTED BY JOHN
von NEUMANN AND OSKAR MORGENSTERN (1944)
 JOHN FORBES NASH Jr. INVENTS CONCEPT OF NASH EQUILIBRIUM
(1950)
 JOHN HARSANYI, JOHN FORBES NASH AND REINHARD SELTEN WON
NOBEL PRIZE IN ECONOMICS FOR GAME THEORY (1994)

5.  PSYCHOLOGY
 LAW
 MILITARY STRATEGY
 MANAGEMENT
 SPORTS
 GAME PLAYING
MATHEMATICS
COMPUTER SCIENCE
BIOLOGY
ECONOMICS
POLITICAL SCIENCE
INTERNATIONAL RELATIONS
PHILOSOPHY

6. PLAYERS : WHO IS INTERACTING?
STRATEGIES : WHAT ARE THEIR OPTIONS?
PAYOFFS : WHAT ARE THEIR INCENTIVES?
INFORMATION : WHAT DO THEY KNOW?
RATIONALITY : HOW DO THEY THINK?

7. COOPERATIVE OR NON COOPERATIVE
ZERO-SUM AND NON-ZERO SUM
SIMULTANEOUS AND SIQUENTIAL
PERFECT INFORMATION AND IMPERFECT INFORMATION
FINITE AND INFINITE STRATEGIES

8. THE UPPER VALUE OF THE GAME IS EQUAL TO THE
MINIMUM OF THE MAXIMUM VALUES IN THE COLUMNS.
THE LOWER VALUE OF THE GAME IS EQUAL TO THE
MAXIMUM VALUES OF THE MINIMUM VALUES IN THE ROW.

9. B
A
Y1 Y2 MINIMUM
X1
X2
MAXIMUM
6
7
10 7
6
-12
10
-12
6
7

10. A MIXED STRATEGY GAME EXISTS WHEN THERE IS NO
SADDLE POINT. EACH PLAYER WILL THEN OPTIMIZE
THEIR EXPECTED GAIN BY DETERMINING THE
PERCENT OF TIME TO USE EACH STRATEGY.

11. A
B
B
BELIEVES
B
DOESN’T
BELIEVE
A
BLUFFS
A
DOESN’T
BLUFF
1
0.50
0

12. A STABLE STATE OF A
SYSTEM INVOLVING THE
INTERACTION OF
DIFFERENT
PARTICIPANTS, IN WHICH
NO PARTICIPANT CAN
GAIN BY A UNILATERAL
CHANGE OF STRATEGY IF
THE STRATEGIES OF THE
OTHERS REMAIN
UNCHANGED.

13. For example, imagine a game between Tom and Sam.
In this simple game, both players can choose strategy
A, to receive $1, or strategy B, to lose $1. Logically,
both players choose strategy A and receive a payoff of
$1. If you revealed Sam's strategy to Tom and vice
versa, you see that no player deviates from the
original choice. Knowing the other player's move
means little and doesn't change either player's
behaviour. The outcome A, A represents a Nash
Equilibrium.

14. PENNY MATCHING :
• EACH OF THE TWO PLAYERS HAS A PENNY.
• TWO PLAYERS MUST SIMULTANEOUSLY
CHOOSE WHETHER TO SHOW THE HEAD OR
THE TAIL.
• BOTH PLAYERS KNOW THE FOLLOWING
RULES:
1. IF TWO PENNIES MATCH (BOTH HEADS
OR BOTH TAILS) THEN PLAYER 2 WINS
PLAYER 1’S PENNY.
2. OTHERWISE, PLAYER 1 WINS PLAYER 2’S
PENNY.
-1 , 1
1 , -1 -1 , 1
1 , -1
HEAD TAIL
PLAYER 2
HEAD
TAIL
PLAYER1

15. • NO COMMUNICATION
- STRATEGIES MUST BE UNDERTAKEN WITHOUT THE FULL
KNOWLEDGE OF WHAT THE OTHER PLAYERS (PRISONERS)
WILL DO.
• PLAYERS (PRISONERS) DEVELOP DOMINANT STRATEGIES BUT ARE
NOT NECESSARILY THE BEST ONE.
- ALBERT W. TUCKER

16. 10 YEARS FOR BILL
1 YEAR FOR TED
BOTH GET
5 YEARS
1 YEAR FOR BILL
1O YEARS FOR TED
BOTH GET
3 YEARS
CONFESS
NOT CONFESS
BILL
CONFESS NOT CONFESS
TED

17.  DEBOTTAM PAUL CHOUDHURY
 ISHITA BOSE
 SAUMYAJIT BANDAPADHYAY
 DEBOSMITA MAJUMDER
 JHILIK CHATTERJEE