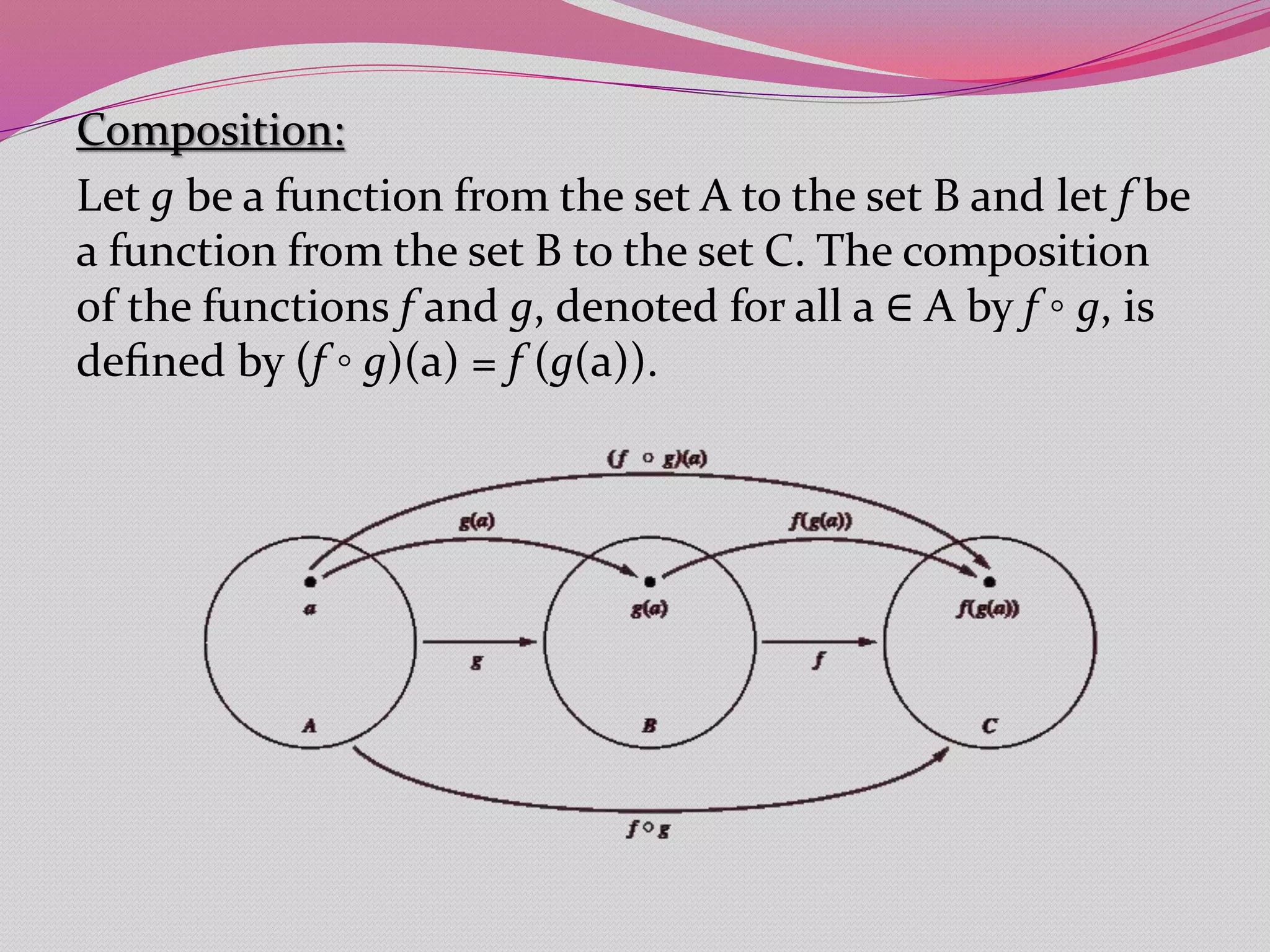
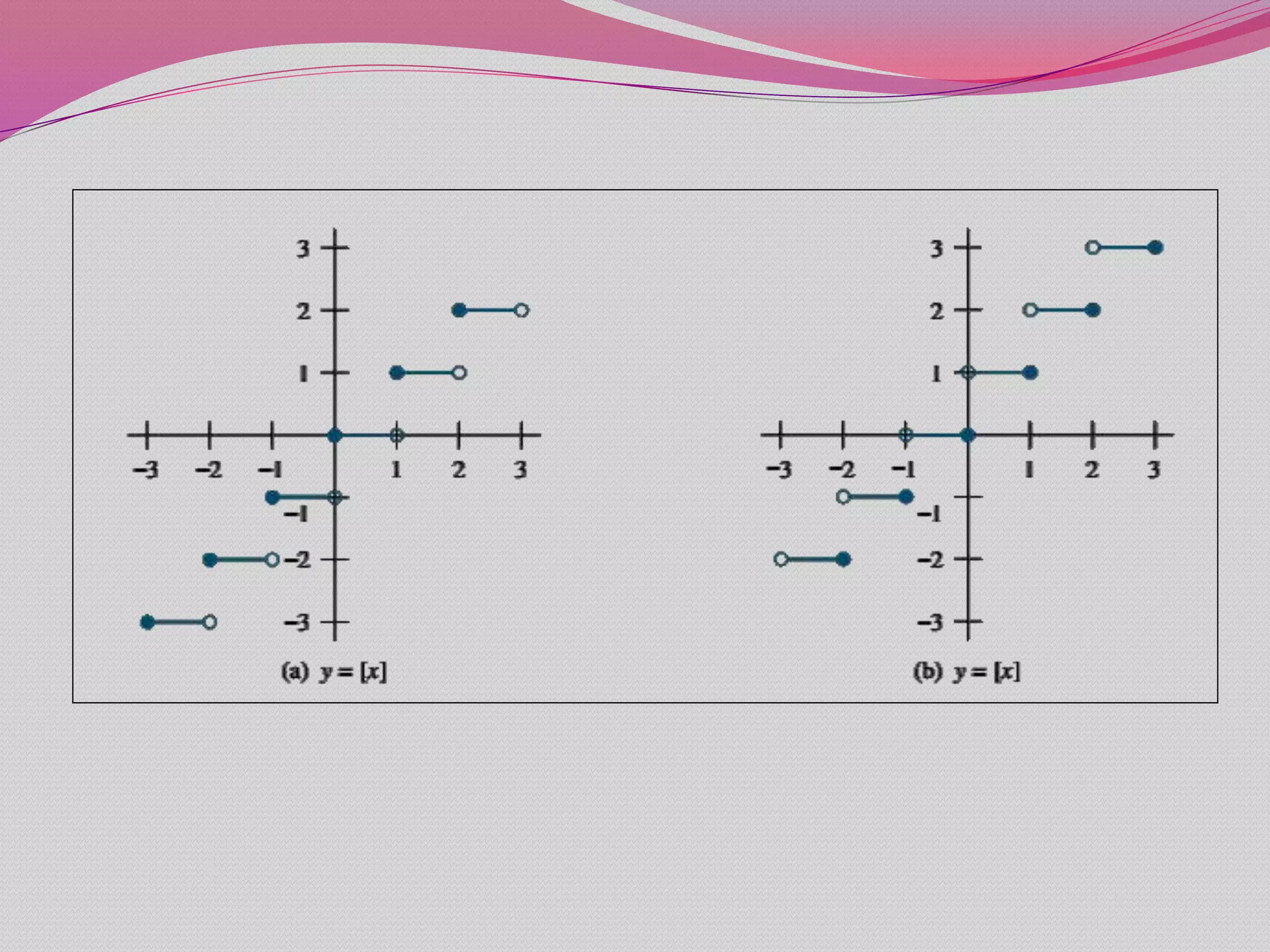
The document defines key concepts related to functions including: domain, codomain, range, one-to-one (injective) functions, increasing/decreasing functions, onto (surjective) functions, bijective functions, inverse functions, function composition, and floor and ceiling functions. It provides examples to illustrate these concepts and determine if specific functions have given properties.

1. Functions

2. Function:
Let A and B be nonempty sets. A function f from A to B
is an assignment of exactly one element of B to each
element of A.
 If is a function from A to B, we write
f : A → B
f(a) = b
 A is the domain of f and B is the codomain of f.
 b is the image of a and a is the pre-image of b.
 The range of f is the set of all images of elements of A.

3. Injective Function:
A function f is said to be one-to-one or injective if and
only if f(a) = f(b) implies that a = b for all a and b in the
domain of f.
 x  y (f(x) = f(y)  x = y)
 Determine whether the function f from {a, b, c, d} to {1, 2, 3,
4, 5} with f(a) = 4, f(b) = 5, f (c) = 1, and f(d) = 3 is one-to-
one.
 Solution: The function f is one-to-one because f takes on
different values at the four elements of its domain.

4.  If the function g: Z → Z is defined by the rule g(n) = n2
for all n ∈ Z, then is g one-to-one?
 Solution:
Let n1 = 2 and n2 =−2.
g(n1) = g(2) = 4
g(n2) = g(−2) = 4.
Hence g(n1) = g(n2) but n1≠n2,

5.  If the function f : R → R is defined by the rule
f(x)=4x−1, for all real numbers x, then is f one-to-one?
 Solution:
Suppose x and y are real numbers such that f(x)=f(y).
[We must show that x = y.]
By definition of f , 4 x − 1 = 4 y − 1.
4 x = 4 y
x = y

6. Increasing and Decreasing function:
A function f whose domain and codomain is a subset of
real numbers is called increasing if f(x) ≤ f(y), and
strictly increasing if f(x)<f(y), whenever x<y and x
and y are in the domain of f.
Similarly, f is called decreasing if f(x) ≥ f(y), and strictly
decreasing if f(x)>f(y), whenever x<y and x and y are in
the domain of f.
Surjective Function:
A function f from A to B is called onto, or surjective, if
and only if for every element b ∈ B there is an element a
∈ A with f(a) = b.

7.  Is the function f(x) = x2 from the set of integers to the
set of integers onto?
 Solution:
The function f is not onto.
(Example : there is no integer x with x2 =−1)
 Is the function f(x) = x + 1 from the set of integers to
the set of integers onto?
 Solution:
This function is onto, because for every integer y there
is an integer x such that f (x) = y.

8. Bijective Function:
The function f is a one-to-one correspondence, or a
bijective function, if it is both one-to-one and onto.
Inverse Function:
Let f be a one-to-one correspondence from the set A to
the set B. The inverse function of f is the function that
assigns to an element b belonging to B the unique
element a in A such that f(a) = b.
The inverse function of f is denoted by f -1. Hence,
f -1(b) = a when f(a) = b.

9.  Let f : Z → Z be such that f(x) = x + 1. Is f invertible,
and if it is, what is its inverse?
 Solution:
The function f has an inverse because it is a one-to-
one correspondence
f -1 (y) = y − 1.
 Let f be the function from R to R with f(x) = x2.Is f
invertible?
 Solution:
Because f(−2) = f(2) = 4, f is not one-to-one.

10. Composition:
Let g be a function from the set A to the set B and let f be
a function from the set B to the set C. The composition
of the functions f and g, denoted for all a ∈ A by f ◦ g, is
defined by (f ◦ g)(a) = f (g(a)).

11.  Let f and g be the functions from the set of integers to
the set of integers defined by f(x) = 2x + 3 and g(x) =
3x+2. What is the composition of f and g? What is the
composition of g and f ?
 Solution:
(f ◦ g)(x) = f(g(x)) = f(3x + 2) = 2(3x + 2) + 3 = 6x + 7
(g ◦ f )(x) = g(f(x)) = g(2x + 3) = 3(2x + 3) + 2 = 6x + 11.
Composition of a function and its inverse:
(f -1 ◦f)(x) = f -1(f(x)) = x

12. Floor and Ceiling Function:
The floor and ceiling functions map the real
numbers onto the integers (RZ).
The floor function assigns to rR the largest zZ
with zr, denoted by r.
Examples: 2.3 = 2, 2 = 2, 0.5 = 0, -3.5 = -4
The ceiling function assigns to rR the smallest
zZ with zr, denoted by r.
Examples: 2.3 = 3, 2 = 2, 0.5 = 1, -3.5 = -3

14. Solution:
      yxyxyx andnumbersrealallforthatdisproveorProve 
  11
2
1
2
1
2
1
and
2
1
Let





 yx
2
2
1
2
1












     yxyx Therefore,