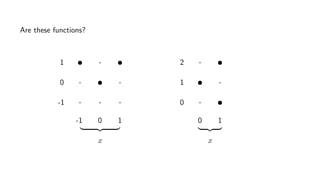
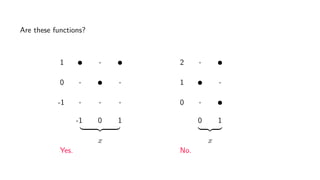
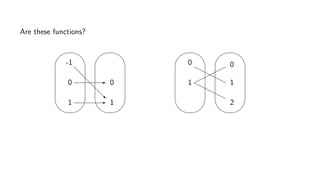
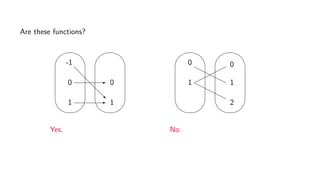
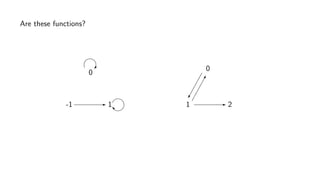
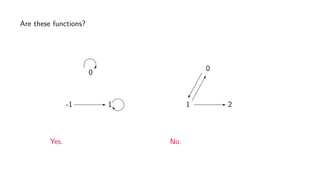
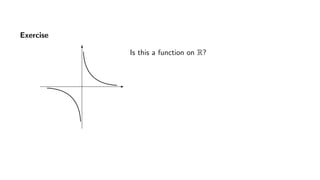
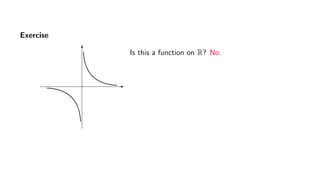
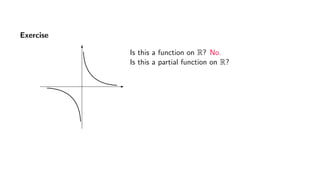
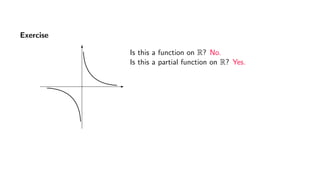
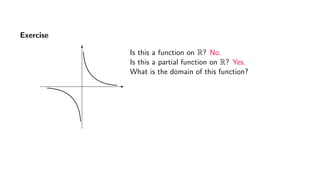
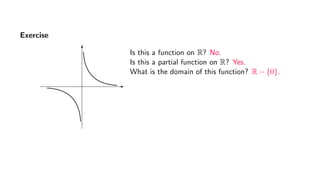
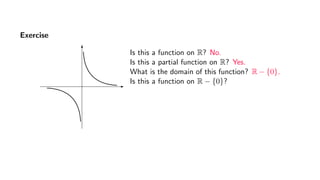
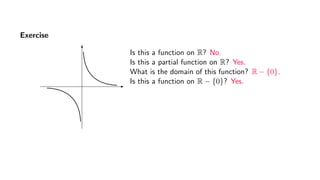
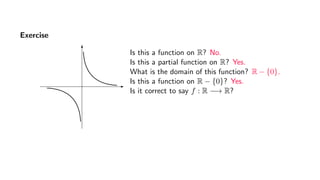
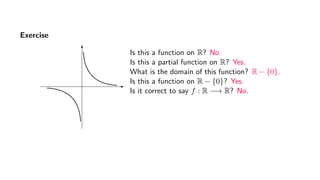
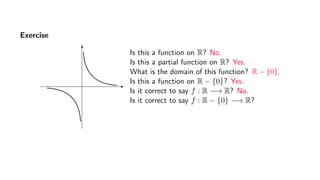
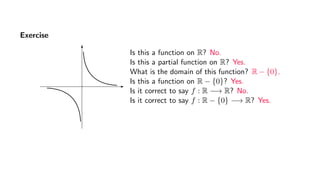
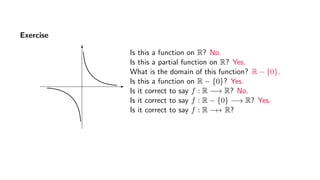
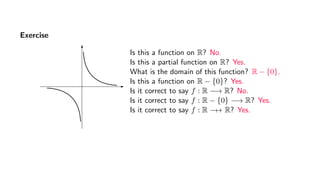
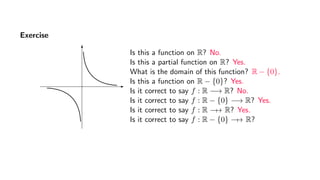
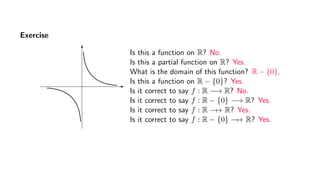
The document provides an overview of set theory, focusing on the definition and visualization of functions, existence and uniqueness in first-order logic, and the distinctions between total and partial functions. It explains how to determine if a relation is a function, employing vertical line tests and offering exercises to evaluate understanding. The text addresses specific functions, their domains, and conditions for them to be deemed total or partial functions.

1. Introduction to set theory and to methodology and philosophy of
mathematics and computer programming
Defining and visualizing functions
An overview
by Jan Plaza
c 2017 Jan Plaza
Use under the Creative Commons Attribution 4.0 International License
Version of November 4, 2017

2. Existence and uniqueness
How to express in first-order logic “there exists unique y s.t. A(y)”
without using the abbreviation ∃!y A(y) ?

3. Existence and uniqueness
How to express in first-order logic “there exists unique y s.t. A(y)”
without using the abbreviation ∃!y A(y) ?
Existence: ∃y A(y).
Uniqueness: ∀y1,y2 (A(y1) ∧ A(y2) → y1 =y2).

4. Existence and uniqueness; Functions
How to express in first-order logic “there exists unique y s.t. A(y)”
without using the abbreviation ∃!y A(y) ?
Existence: ∃y A(y).
Uniqueness: ∀y1,y2 (A(y1) ∧ A(y2) → y1 =y2).
Definition
A function is any binary relation f such that ∀x ∀y1,y2 (xfy1 ∧ xfy2 → y1 =y2),
or equivalently, ∀x (∃y xfy → ∀y1,y2 (xfy1 ∧ xfy2 → y1 =y2)).

5. Existence and uniqueness; Functions
How to express in first-order logic “there exists unique y s.t. A(y)”
without using the abbreviation ∃!y A(y) ?
Existence: ∃y A(y).
Uniqueness: ∀y1,y2 (A(y1) ∧ A(y2) → y1 =y2).
Definition
A function is any binary relation f such that ∀x ∀y1,y2 (xfy1 ∧ xfy2 → y1 =y2),
or equivalently, ∀x (∃y xfy → ∀y1,y2 (xfy1 ∧ xfy2 → y1 =y2)).
This means: if there is y s.t. xfy then such a y is unique.

6. Existence and uniqueness; Functions
How to express in first-order logic “there exists unique y s.t. A(y)”
without using the abbreviation ∃!y A(y) ?
Existence: ∃y A(y).
Uniqueness: ∀y1,y2 (A(y1) ∧ A(y2) → y1 =y2).
Definition
A function is any binary relation f such that ∀x ∀y1,y2 (xfy1 ∧ xfy2 → y1 =y2),
or equivalently, ∀x (∃y xfy → ∀y1,y2 (xfy1 ∧ xfy2 → y1 =y2)).
This means: if there is y s.t. xfy then such a y is unique.
Definition. Let f be a function.
1. Let x ∈ domain(f). The value of f at x , f(x) , is the unique y such that xfy.
2. f maps x to y , denoted f : x → y or x
f
→ y , if xfy.

7. x
Is this a function?

8. x
Is this a function? Yes.

9. x
Is this a function?

10. x
Is this a function? Yes.

11. x
Is this a function?

12. x
Is this a function? No. More than one value of y is paired with the same value of x.

13. Are these functions?
x x

14. Are these functions?
x
No.
x
Yes.

15. Are these functions?
{ −1, 1 , 0, 0 , 1, 1 },
i.e.
x y
−1 1
0 0
1 1
{ 1, 0 , 0, 1 , 1, 2 },
i.e.
x y
1 0
0 1
1 2

16. Are these functions?
{ −1, 1 , 0, 0 , 1, 1 },
i.e.
x y
−1 1
0 0
1 1
Yes.
{ 1, 0 , 0, 1 , 1, 2 },
i.e.
x y
1 0
0 1
1 2
No.

17. Are these functions?
-1
0
1
-1 0 1
x
0
1
2
0 1
x

18. Are these functions?
-1
0
1
-1 0 1
x
Yes.
0
1
2
0 1
x
No.

19. Are these functions?
-1
0
1
0
1
0
1
0
1
2

20. Are these functions?
-1
0
1
0
1
Yes.
0
1
0
1
2
No.

21. Are these functions?
0
-1 1
0
1 2

22. Are these functions?
0
-1 1
Yes.
0
1 2
No.

23. Terminology: total/partial, on
Definition. Let f be a function.
f is on X or f is a (total) function on X if domain(f) = X.
Definition. f is a partial function on X if there is X ⊆X s.t. f is a function onX .
Fact. If f is a partial function on X, then f is a total function on domain(f).
If f is a function and X ⊇ domain(f), then f is a partial function on X.
Fact. Consider these conditions:
1. f is a binary relation,
2. domain(f) ⊆ X,
3. for every x ∈ X, f maps x to at most one value,
4. for every x ∈ X, f maps x to least one value.
Then:
f is a function on X iff f satisfies conditions 1-4;
f is a partial function on X iff f satisfies conditions 1-3.

24. Vertical line tests on the Cartesian plane are the following.
Let G be a subset of the Cartesian plane.
G is the graph of a function from R to R
iff every straight line parallel to the y axis intersects G in exactly one point.
G is the graph of a partial function from R to R
iff every straight line parallel to the y axis intersects G in at most one point.
Vertical line tests in discrete Cartesian diagrams are the following.
Let G be a subset of X × Y in a discrete Cartesian diagram.
G is the graph of a function from X to Y
iff every column in the diagram contains exactly one point of G.
G is the graph of a partial function from X to Y
iff every column in the diagram contains at most one point of G.

25. Terminology: from, to
Definition. Let f be a function.
1. f is to/into Y if range(f) ⊆ Y .
2. f is (a total function) from X to Y , denoted f : X −→ Y or X
f
−→ Y ,
if domain(f)=X and range(f) ⊆ Y .
Definition
f is a partial function from X to Y , denoted f : X −→ Y or X
f
−→ Y ,
if there exists X ⊆ X such that f : X −→ Y .
f : X −→ Y f : X −→ Y
domain(f) ⊆ X domain(f) = X
range(f) ⊆ Y range(f) ⊆ Y
Our definitions imply that the term “to/into Y ” applies to partial functions as well:
for any partial function f, f is to/into Y iff range(f) ⊆ Y .

26. Exercise
Is this a function on R?

27. Exercise
Is this a function on R? No.

28. Exercise
Is this a function on R? No.
Is this a partial function on R?

29. Exercise
Is this a function on R? No.
Is this a partial function on R? Yes.

30. Exercise
Is this a function on R? No.
Is this a partial function on R? Yes.
What is the domain of this function?

31. Exercise
Is this a function on R? No.
Is this a partial function on R? Yes.
What is the domain of this function? R − {0}.

32. Exercise
Is this a function on R? No.
Is this a partial function on R? Yes.
What is the domain of this function? R − {0}.
Is this a function on R − {0}?

33. Exercise
Is this a function on R? No.
Is this a partial function on R? Yes.
What is the domain of this function? R − {0}.
Is this a function on R − {0}? Yes.

34. Exercise
Is this a function on R? No.
Is this a partial function on R? Yes.
What is the domain of this function? R − {0}.
Is this a function on R − {0}? Yes.
Is it correct to say f : R −→ R?

35. Exercise
Is this a function on R? No.
Is this a partial function on R? Yes.
What is the domain of this function? R − {0}.
Is this a function on R − {0}? Yes.
Is it correct to say f : R −→ R? No.

36. Exercise
Is this a function on R? No.
Is this a partial function on R? Yes.
What is the domain of this function? R − {0}.
Is this a function on R − {0}? Yes.
Is it correct to say f : R −→ R? No.
Is it correct to say f : R − {0} −→ R?

37. Exercise
Is this a function on R? No.
Is this a partial function on R? Yes.
What is the domain of this function? R − {0}.
Is this a function on R − {0}? Yes.
Is it correct to say f : R −→ R? No.
Is it correct to say f : R − {0} −→ R? Yes.

38. Exercise
Is this a function on R? No.
Is this a partial function on R? Yes.
What is the domain of this function? R − {0}.
Is this a function on R − {0}? Yes.
Is it correct to say f : R −→ R? No.
Is it correct to say f : R − {0} −→ R? Yes.
Is it correct to say f : R −→ R?

39. Exercise
Is this a function on R? No.
Is this a partial function on R? Yes.
What is the domain of this function? R − {0}.
Is this a function on R − {0}? Yes.
Is it correct to say f : R −→ R? No.
Is it correct to say f : R − {0} −→ R? Yes.
Is it correct to say f : R −→ R? Yes.

40. Exercise
Is this a function on R? No.
Is this a partial function on R? Yes.
What is the domain of this function? R − {0}.
Is this a function on R − {0}? Yes.
Is it correct to say f : R −→ R? No.
Is it correct to say f : R − {0} −→ R? Yes.
Is it correct to say f : R −→ R? Yes.
Is it correct to say f : R − {0} −→ R?

41. Exercise
Is this a function on R? No.
Is this a partial function on R? Yes.
What is the domain of this function? R − {0}.
Is this a function on R − {0}? Yes.
Is it correct to say f : R −→ R? No.
Is it correct to say f : R − {0} −→ R? Yes.
Is it correct to say f : R −→ R? Yes.
Is it correct to say f : R − {0} −→ R? Yes.

42. Example
1. Let f ={ 0, −1 , 1, 0 , 2, 3 }.
f is a function from {0, 1, 2} to Z.
f is also a function from {0, 1, 2} to {−1, 0, 3}.
2. Alternatively we could specify it as:
a function f on {0, 1, 2} s.t. f(0)=−1, f(1)=0, f(2)=3.
3. Alternatively we could specify it as:
a function f on {0, 1, 2} s.t. f : 0 → −1, f : 1 → 0, f : 2 → 3.
4. Alternatively we could specify it as:
a function f on {0, 1, 2} s.t. f(x)=x2 − 1.
5. Let g be a function on {0, 1, 2, 3} s.t. g(x)=x2 − 1.
Although g and f are defined by the same formula,
they are different functions
because they have different domains.

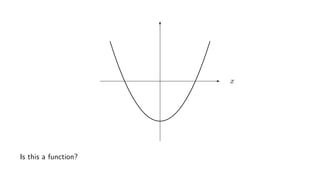
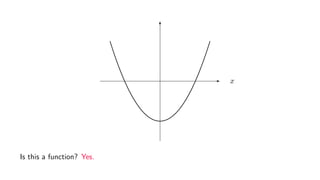
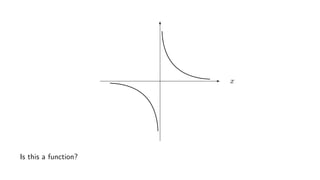
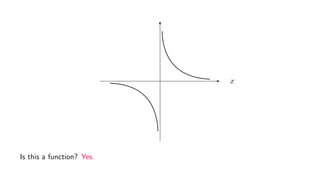
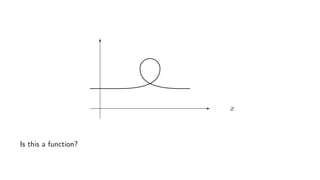
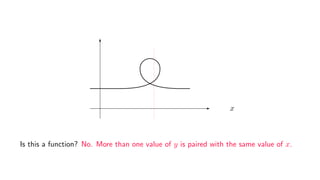
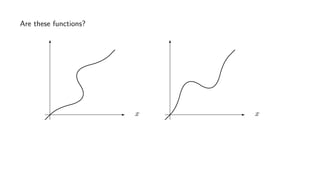
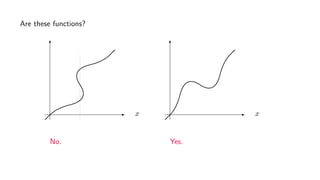
43. Example
1. Expression y =
√
1 − x2 does not define a function on R,
but it defines a function on [−1, 1].
2. Expression y = ±
√
1 − x2 specifies coordinates of points of a unit circle,
however it does not define a function on [−1, 1].

44. Exercise
Consider the formula y =
√
x.
(Recall that for x = 9 we have just y = 3,
because the definition of square root requires it to be non-negative.)
1. Does this formula define a function from R to R?

45. Exercise
Consider the formula y =
√
x.
(Recall that for x = 9 we have just y = 3,
because the definition of square root requires it to be non-negative.)
1. Does this formula define a function from R to R? No.

46. Exercise
Consider the formula y =
√
x.
(Recall that for x = 9 we have just y = 3,
because the definition of square root requires it to be non-negative.)
1. Does this formula define a function from R to R? No.
2. Does this formula define a function from {u ∈ R : u 0} to R?

47. Exercise
Consider the formula y =
√
x.
(Recall that for x = 9 we have just y = 3,
because the definition of square root requires it to be non-negative.)
1. Does this formula define a function from R to R? No.
2. Does this formula define a function from {u ∈ R : u 0} to R? Yes.

48. Exercise
Consider the formula y =
√
x.
(Recall that for x = 9 we have just y = 3,
because the definition of square root requires it to be non-negative.)
1. Does this formula define a function from R to R? No.
2. Does this formula define a function from {u ∈ R : u 0} to R? Yes.
3. Does this formula define a partial function from R to R?

49. Exercise
Consider the formula y =
√
x.
(Recall that for x = 9 we have just y = 3,
because the definition of square root requires it to be non-negative.)
1. Does this formula define a function from R to R? No.
2. Does this formula define a function from {u ∈ R : u 0} to R? Yes.
3. Does this formula define a partial function from R to R? Yes.

50. Exercise
Consider the formula y =
√
x.
(Recall that for x = 9 we have just y = 3,
because the definition of square root requires it to be non-negative.)
1. Does this formula define a function from R to R? No.
2. Does this formula define a function from {u ∈ R : u 0} to R? Yes.
3. Does this formula define a partial function from R to R? Yes.
4. Does this formula define a function from {u ∈ R : u 0} to Q?

51. Exercise
Consider the formula y =
√
x.
(Recall that for x = 9 we have just y = 3,
because the definition of square root requires it to be non-negative.)
1. Does this formula define a function from R to R? No.
2. Does this formula define a function from {u ∈ R : u 0} to R? Yes.
3. Does this formula define a partial function from R to R? Yes.
4. Does this formula define a function from {u ∈ R : u 0} to Q? No.

52. Exercise
Consider the formula y =
√
x.
(Recall that for x = 9 we have just y = 3,
because the definition of square root requires it to be non-negative.)
1. Does this formula define a function from R to R? No.
2. Does this formula define a function from {u ∈ R : u 0} to R? Yes.
3. Does this formula define a partial function from R to R? Yes.
4. Does this formula define a function from {u ∈ R : u 0} to Q? No.
5. Does this formula define a function from {u ∈ R : u 0} to {u ∈ R : u 0}?

53. Exercise
Consider the formula y =
√
x.
(Recall that for x = 9 we have just y = 3,
because the definition of square root requires it to be non-negative.)
1. Does this formula define a function from R to R? No.
2. Does this formula define a function from {u ∈ R : u 0} to R? Yes.
3. Does this formula define a partial function from R to R? Yes.
4. Does this formula define a function from {u ∈ R : u 0} to Q? No.
5. Does this formula define a function from {u ∈ R : u 0} to {u ∈ R : u 0}?
Yes.

54. Exercise
Are the following statements correct?
1. Let f1, f2 be functions.
If domain(f1) = domain(f2) and f1 ⊆ f2, then f1 = f2.

55. Exercise
Are the following statements correct?
1. Let f1, f2 be functions.
If domain(f1) = domain(f2) and f1 ⊆ f2, then f1 = f2. Yes.

56. Exercise
Are the following statements correct?
1. Let f1, f2 be functions.
If domain(f1) = domain(f2) and f1 ⊆ f2, then f1 = f2. Yes.
2. Let R1, R2 be binary relations.
If domain(R1) = domain(R2) and R1 ⊆ R2, then R1 = R2.

57. Exercise
Are the following statements correct?
1. Let f1, f2 be functions.
If domain(f1) = domain(f2) and f1 ⊆ f2, then f1 = f2. Yes.
2. Let R1, R2 be binary relations.
If domain(R1) = domain(R2) and R1 ⊆ R2, then R1 = R2. No.

58. Exercise
Are the following statements correct?
1. Let f1, f2 be functions.
If domain(f1) = domain(f2) and f1 ⊆ f2, then f1 = f2. Yes.
2. Let R1, R2 be binary relations.
If domain(R1) = domain(R2) and R1 ⊆ R2, then R1 = R2. No.
3. Let f1, f2 be partial functions on the same set X.
If f1 ⊆ f2, then f1 = f2.

59. Exercise
Are the following statements correct?
1. Let f1, f2 be functions.
If domain(f1) = domain(f2) and f1 ⊆ f2, then f1 = f2. Yes.
2. Let R1, R2 be binary relations.
If domain(R1) = domain(R2) and R1 ⊆ R2, then R1 = R2. No.
3. Let f1, f2 be partial functions on the same set X.
If f1 ⊆ f2, then f1 = f2. No.
Whenever the answer is negative, provide a counter-example.

60. Note
1. An attempt to define f : Q −→ Z:
f(m
n ) = m + n, where m, n ∈ Z.
This is not correct, because
1
2 = 2
4 but f(1
2) = 1 + 2 = 3=6 = 2 + 4 = f(2
4)
violating ∀x,y1,y2 (xfy1 ∧ xfy2 → y1 =y2).
2. An attempt to define g : Q −→ Z:
let g(0)=1 and
let g(m
n ) = m + n where m, n ∈ Z, m=0, n > 0,
and m and n do not have a common divisor greater than 1.
This is correct.
(We have used a canonical form of rational numbers.)
3. Every rational number has many representations (1
2 = 2
4 = ...).
To be correct, the definition must be
independent of the representation .

61. Exercise
Let Q+ be the set of all positive rational numbers.
Are these attempts to define a function correct?
1. f : Q −→ Q s.t. f(m
n ) = n
m where m, n ∈ Z.

62. Exercise
Let Q+ be the set of all positive rational numbers.
Are these attempts to define a function correct?
1. f : Q −→ Q s.t. f(m
n ) = n
m where m, n ∈ Z. No.

63. Exercise
Let Q+ be the set of all positive rational numbers.
Are these attempts to define a function correct?
1. f : Q −→ Q s.t. f(m
n ) = n
m where m, n ∈ Z. No.
2. f : Q+ −→ Q+ s.t. f(m
n ) = n
m where m, n ∈ Z.

64. Exercise
Let Q+ be the set of all positive rational numbers.
Are these attempts to define a function correct?
1. f : Q −→ Q s.t. f(m
n ) = n
m where m, n ∈ Z. No.
2. f : Q+ −→ Q+ s.t. f(m
n ) = n
m where m, n ∈ Z. Yes.
Show this by proving:
if m1, n1, m2, n2 ∈ Z and m1
n1
, m2
n2
∈ Q+ and m1
n1
= m2
n2
then n1
m1
= n2
m2
.

65. Note. An attempt to to model the concept “mother of”:
1. Persons is a non-empty set,
2. Persons is a finite set,
3. motherOf : Persons −→ Persons
(i.e. every person has a unique mother, who is a person),
4. motherOf is a function such that for every p in its domain:
p=motherOf(p),
p=motherOf(motherOf(p)),
p=motherOf(motherOf(motherOf(p))),
etc. (i.e. there are no cycles).
These conditions are contradictory.
(The same problem occurs with theSupervisorOf in employee databases.)
To see why, try drawing directed graphs
showing a function motherOf on a three-element set Persons.