This document contains solutions to problems related to basic conservation laws in fluid mechanics. Specifically: - Problem 1.1 derives the equation of continuity in Cartesian coordinates from the net inflow/outflow of a control volume. - Problems 1.2-1.4 derive the equation of continuity in cylindrical and spherical polar coordinates by applying transformations to the Cartesian form. - Problem 1.5 provides expressions for converting partial derivatives between Cartesian, cylindrical, and spherical coordinate systems, which are needed for applying conservation laws in different frames of reference.

1. SOLUTIONS MANUALFOR
by
Fundamental
Mechanics of Fluids
Fourth Edition
I.G. Currie

3. SOLUTIONS MANUAL FOR
by
Fundamental
Mechanics of Fluids
Fourth Edition
I.G. Currie

4. CRC Press
Taylor & Francis Group
6000 Broken Sound Parkway NW, Suite 300
Boca Raton, FL 33487-2742
© 2013 by Taylor & Francis Group, LLC
CRC Press is an imprint of Taylor & Francis Group, an Informa business
No claim to original U.S. Government works
Printed in the United States of America on acid-free paper
Version Date: 20120723
International Standard Book Number: 978-1-4665-1696-0 (Paperback)
This book contains information obtained from authentic and highly regarded sources. Reasonable efforts have been made to publish reliable data and
information, but the author and publisher cannot assume responsibility for the validity of all materials or the consequences of their use. The authors and
publishers have attempted to trace the copyright holders of all material reproduced in this publication and apologize to copyright holders if permission
to publish in this form has not been obtained. If any copyright material has not been acknowledged please write and let us know so we may rectify in any
future reprint.
Except as permitted under U.S. Copyright Law, no part of this book may be reprinted, reproduced, transmitted, or utilized in any form by any electronic,
mechanical, or other means, now known or hereafter invented, including photocopying, microfilming, and recording, or in any information storage or
retrieval system, without written permission from the publishers.
For permission to photocopy or use material electronically from this work, please access www.copyright.com (http://www.copyright.com/) or contact
the Copyright Clearance Center, Inc. (CCC), 222 Rosewood Drive, Danvers, MA 01923, 978-750-8400. CCC is a not-for-profit organization that provides
licenses and registration for a variety of users. For organizations that have been granted a photocopy license by the CCC, a separate system of payment
has been arranged.
Trademark Notice: Product or corporate names may be trademarks or registered trademarks, and are used only for identification and explanation
without intent to infringe.
Visit the Taylor & Francis Web site at
http://www.taylorandfrancis.com
and the CRC Press Web site at
http://www.crcpress.com

5. 1
BASIC CONSERVATION LAWS

7. BASIC CONSERVATION LAWS
Page 1-1
Problem 1.1
Inflow through x = constant: u y z  
Outflow through x x = constant: ( )u y z u y z x
x
      

 

Net inflow through x = constant surfaces: ( )u x y z
x
   

 

Net inflow through y = constant surfaces: ( )v x y z
y
   

 

Net inflow through z = constant surfaces: ( )w x y z
z
   

 

But the rate at which the mass is accumulating inside the control volume is:
( )x y z
t
  


Then the equation of mass conservation becomes:
( ) ( ) ( )x y z u v w x y z
t x y z

        
    
         
Taking the limits as the quantities , andx y z   become vanishingly small, we get:
( ) ( ) ( ) 0u v w
t x y z

  
   
   
   

8. BASIC CONSERVATION LAWS
Page 1-2
Problem 1.2
Inflow through R = constant: Ru R z  
Outflow through R R = constant: ( )R Ru R z u R z R
R
      

 

Net inflow through R = constant surfaces: ( )RRu R z
R
   

 

Net inflow through  = constant surfaces: ( )u R z   


 

Net inflow through z = constant surfaces: ( )zu R R z
z
   

 

But the rate at which the mass is accumulating inside the control volume is:
( )R R z
t
   


Then the equation of mass conservation becomes:
( ) ( ) ( )R zR R z Ru u R u R z
t R z


        

    
         
Taking the limits as the quantities , andR z   become vanishingly small, we get:
1 1
( ) ( ) ( ) 0R zRu u u
t R R R z


  

   
   
   

9. BASIC CONSERVATION LAWS
Page 1-3
Problem 1.3
Inflow through r = constant: 2
sinru r   
Outflow through r r = constant: 2
sinru r   
2
( sin )rr u r
r
    

 

Net inflow through r = constant surfaces: 2
( )sinrr u r
r
    

 

Net inflow through  = constant surfaces: ( sin )u r r    


 

Net inflow through  = constant surfaces: ( )u r r   


 

But the rate at which the mass is accumulating inside the control volume is:
2
( sin )r r
t
    


Then the equation of mass conservation becomes:
2 2
sin ( )sin ( sin ) ( )rr r r u r u r u r
t r
 

           
 
    
         
Taking the limits as the quantities , andr   become vanishingly small, we get:
2
2
1 1 1
( ) ( sin ) ( ) 0
sin sin
rr u u u
t r r r r
 

   
   
   
   
   

10. BASIC CONSERVATION LAWS
Page 1-4
Problem 1.4
Using the given transformation equations gives:
2 2 2
2
2 2
and tan
2 2 2 cos cos
1 sin 1
and sec sin
cos
y
R x y
x
R R
R x R
x x
y
x x R x R

 
  
 

  
 
    
 
 
      
 
Using these results, the derivatives with respect to andx y transform as follows:
sin
cos
cos
sin
R
x x R x R R
R
y y R y R R
z z
 

 
 

 
      
   
      
      
   
      
 

 
Using these results and the relationships between the Cartesian and cylindrical vector
components, we get the following expressions for the Cartesian terms in the continuity equation:
sin
( ) cos [ ( cos sin )] [( ( cos sin )]R Ru u u u u
x R R
 

       

  
   
  
cos
( ) sin [ ( sin cos )] [( ( sin cos )]R Rv u u u u
y R R
 

       

  
   
  
Adding these two terms and simplifying produces the following equation:
1
( ) ( ) ( ) ( )
1 1
( ) ( )
R
R
R
u
u v u u
x y R R R
Ru u
R R R



   

 

   
   
   
 
 
 
Substituting this result into the full continuity equation yields the following result:
1 1
( ) ( ) ( ) 0R zRu u u
t R R R z


  

   
   
   

11. BASIC CONSERVATION LAWS
Page 1-5
Problem 1.5
The equations that connect the two coordinate systems are as follows:
2
2 2 2 2 2
2 2 2
sin cos sin sin cos
tan cos
( )
x r y r z r
y z
r x y z
x x y z
    
 
  
    
 
Using the relations given above, the following identities are obtained for the various partial
derivatives:
sin cos sin sin cos
1 1 1
cos cos cos sin sin
1 sin 1 cos
0
sin cos
r r r
x y z
x r y r z r
x r y r z
    
  
    
    
 
  
  
  
  
     
  
  
  
  
Thus the following expressions are obtained for the various Cartesian derivatives:
1 sin
sin cos cos cos
sin
1 1 cos
sin sin cos sin
sin
1
cos sin
r
x x r x x
r
r r
r
y y r y y
r r r
r
z z r z z
r r
 
 

   
  
 
 

   
  
 
 
 

      
  
      
  
  
  
      
  
      
  
  
  
      
  
      
 
 
 
Next we need the Cartesian velocity components expressed in terms of spherical components.
This may be achieved by noting that the velocity vector may be written as follows:
x y z r ru v w u u u        u e e e e e e
Then, if we express the base vectors in spherical coordinates in terms of the base vectors in
Cartesian coordinates, equating components in the previous equation will yield the required
relationships. Thus, noting that:

12. BASIC CONSERVATION LAWS
Page 1-6
sin cos sin sin cosx y z x y zx y z r r r         r e e e e e e
Also, recalling from Appendix A that:
it follows that
sin cos sin sin cos
cos cos cos sin sin
sin cos
i
i i
r x y z
x y z
x y
x x


    
    
 
 

 
  
  
  
r r
e
e e e e
e e e e
e e e
Substituting these expressions into the equation obtained above for the velocity vector, and
equating coefficients of like base vectors, yields the following relationships connecting the
Cartesian and spherical velocity components:
sin cos cos cos sin
sin sin cos sin cos
cos sin
r
r
r
u u u u
v u u u
w u u
 
 

    
    
 
  
  
 
Using these results, and those obtained for the Cartesian derivatives, produces the following
expression for the Cartesian terms that appear in the continuity equation:
2
2
1 1 1
( ) ( ) ( ) ( ) ( sin ) ( )
sin sin
ru v w r u u u
x y z r r r r
       
   
     
    
     
Substituting this result into the full continuity equation yields the following expression:
2
2
1 1 1
( ) ( sin ) ( ) 0
sin sin
rr u u u
t r r r r
 

   
   
   
   
   
Problem 1.6
From Appendix A, the following value is obtained for the convective derivative:
1 2 3 2
1 2 3 2 2 1 1
1 1 1 1 2 1 2
3
1 1 3 3 1 2 3
3 3 1
1
( ) ( ) ( )
( ) ( ) ( ) ( )
a a a a
a a a h a h a
h x x x h x x
a
h a h a
h x x
       
                 
   
    
   
a a
e e e

13. BASIC CONSERVATION LAWS
Page 1-7
Applying this result to cylindrical coordinates, we interpret the various terms as follows:
1 2 3
1 2 3
1 2 3
1 2 3
1 1
R z
R z
a u a u a u
x R x x z
h h R h



  
  
  
  e e e e e e
Using these results, the required term becomes:
 ( ) ( )
R z R R z
R R z z
u u u u u u u
u u u Ru u
R R R R R z R
 
 

         
         
          
e u u
Simplifying the right side of this equation produces the required result:
 
2
( )
R R R
R R z
u u u u u
u u
R R R z
 

  
   
  
e u u
Problem 1.7
We use the same starting equation from Appendix A as in the previous problem. However, since
we are dealing with spherical coordinates here, the various terms are as follows:
1 2 3
1 2 3
1 2 3
1 2 3
1 sin
r
r
a u a u a u
x r x x
h h r h r
 
 
 

  
  
  
  e e e e e e
Using these results, the required term becomes:
 ( ) ( ) ( sin
sin
r r r
r r
u u u u u u u
u u u r u r u
r r r r r r r
   
    
  
          
          
           
e u u
Simplifying the right side of this equation yields the required result:
 
2 2
( )
sin
r r r
r r
u u u u u u u
u
r r r r
   
  
   
   
  
e u u

14. BASIC CONSERVATION LAWS
Page 1-8
Problem 1.8
For a Newtonian fluid, the shear stress tensor is defined by the following equation:
k i j
i j i j
k j i
u u u
x x x
  
   
       
Evaluating the various terms in this expression for Cartesian coordinates ( , ,x y z ) and Cartesian
velocity components ( , ,u v w ) yields the following results:
2
2
2
xx
y y
z z
x y y x
xz z x
y z z y
u v w u
x y z x
u v w v
x y z y
u v w w
x y z z
u v
y x
u w
z x
v w
z y
  
  
  
  
  
  
    
    
    
    
    
    
    
    
    
  
   
  
  
   
  
  
   
  
For a monotonic gas, the Stokes relation requires that 2 /3   . Then the relations obtained
above assume the following special form:
4 2 2
3
4 2 2
3
4 2 2
3
xx
y y
z z
x y y x
xz z x
y z z y
u v w
x y z
v u w
y x z
w u v
z x y
u v
y x
u w
z x
v w
z y






  
  
  
   
   
   
   
   
   
   
   
   
  
   
  
  
   
  
  
   
  

15. BASIC CONSERVATION LAWS
Page 1-9
Problem 1.9
For a Newtonian fluid, the dissipation function is defined by the following equation:
2
k i j j
k j i i
u u u u
x x x x
 
      
               
Evaluating the various terms in this equation for the Cartesian coordinates ( , ,x y z ) and the
Cartesian velocity components ( , ,u v w ), yields the following value for :
2 22 2
2 22
2
u v w u v w
x y z x y z
u v u w v w
y x z x z y
 

            
             
             
          
          
           
For a monotonic gas, the Stokes relation requires that 2 /3   . Then the general expression
for  obtained above assumes the following special form:
2 22 2
2 22
2
2 2 2
3
u v w u v w
x y z x y z
u v u w v w
y x z x z y

             
              
           
          
          
          
Problem 1.10
For steady flow of an inviscid and incompressible fluid, but one for which the density is not
constant, the two-dimensional governing equations are:
( ) ( ) 0u v
x y
u u p
u v
x y x
v v p
u v
x y y
 
 
 
 
 
 
  
  
  
  
  
  
Dividing the continuity equation by 0 and using the definitions of the new velocity
components as given, we get:

16. BASIC CONSERVATION LAWS
Page 1-10
0 0
0 0 0
* *
* *
* *
0
0
u v
x y
u v
u v
x x x y
 
 
  
  
    
    
       
       
                    
The last two terms in the last equation represent the steady-state form of the material derivative
of the square root of the density ratio. For an incompressible fluid, this quantity will be zero.
Then the continuity equation becomes:
* *
0 (1.15)
u u
x x
 
 
 
Adding the original form of the continuity equation to each of the components of the momentum
equation, and dividing throughout by the constant 0 , yields the following form of the
momentum equations:
2
0 0 0
2
0 0 0
1
1
p
u u v
x y x
p
u v v
x y y
 
  
 
  
     
             
     
             
Using the definitions of the new velocity components, these equations become:
   
   
2
0
2
0
* * *
* * *
1
1
p
u u v
x y x
p
u v v
x y y


  
  
  
  
  
  
Expanding the terms on the left side of this equation and using Eq. (1.15) reduces the momentum
equations to those of an incompressible fluid. The resulting equations are as follows:
0
0
* *
* *
* *
* *
* *
0
1
1
u v
x y
u u p
u v
x y x
v v p
u v
x y y


 
 
 
  
  
  
  
  
  

17. 2
FLOW KINEMATICS

19. FLOW KINEMATICS
Page 2-1
Problem 2.1
The following graph was drawn using EXCEL.
__________________________________________________________________________
Problem 2.2
(a) 1
(1 )
But 1 when 0 0
dy v
t
dx u
y t x C
x y t C
Hence at 0t the equation of the streamline is:
y x

20. FLOW KINEMATICS
Page 2-2
1 2
1
(b) 1
1
log(1 )
dx dy
u v
dt t dt
x t C y t C
The condition that 1x y when 0t requires that 1 2 1C C , so that:
1 log(1 ) 1x t y t
Eliminating t between these two equations shows that the equation of the pathline is:
1x
y e
(c) Here, the equations obtained in (b) above are required to satisfy the condition 1x y
when t . This leads to the values 1 1 log(1 )C and 2 1C . Hence the
parametric equations of the streakline are:
log(1 ) 1 log(1 ) 1x t y t
At time 0t these equations become:
1 log(1 ) 1x y
Eliminating the parameter between these two equations yields the following equation
for the streakline at 0t :
1
2 x
y e
Problem 2.3
(a) (1 ) 1 0u x t v w
(1 )
1 1(1 ) at 0t s sdx
x t x C e C e t
ds
21
dy
y s C
ds
But x = y = 1 when s = 0 so that 1 2 1C C . Hence:
and 1s
x e y s
1y
x e

21. FLOW KINEMATICS
Page 2-3
(b) (1 /2)
1(1 ) t tdx
x t x C e
dt
21
dy
y t C
dt
But x = y = 1 when t = 0 so that 1 2 1C C . Hence:
(1 / 2)
and 1t t
x e y t
2
( 1)/2y
x e
(c) As in (b): (1 /2)
1 2andt t
x C e y t C
But x = y = 1 when t = so that (1 /2)
1 2and 1C e C . Hence:
(1 /2) (1 /2) (1 /2)
for 0t t
x e e t
and 1 1 for 0y t t
(1 )(3 )/ 2y y
x e
(d) From the continuity equation:
( ) ( ) ( ) 0
D
u v w
t x y z Dt
u
Hence: (1 )
D
t
Dt
u since (1 )tu here.
i.e. (log ) (1 )
D
t
Dt
Therefore log (1 / 2) logt t C
So that (1 /2)t t
C e
But 0 when t = 0 so that 0C . Hence:
(1 /2)
0
t t
e along the streamline
Problem 2.4
The equations that define the streamlines are as follows:
/(1 )
(1 )
log log
(1 )
or
i i
i i
i i
s t
i i
dx dx ds
ds or
u x t
s
x C
t
x C e

22. FLOW KINEMATICS
Page 2-4
Let 0i ix x when 0s . Then:
/(1 )
0
s t
i ix x e
So that:
0 0 0
x y z
x y z
for any time t .
The equations that define the pathlines are as follows:
(1 )
log log(1 ) log
or (1 )
i i i
i
i i
i i
dx dx x
u or
dt dt t
x t C
x C t
Let 0i ix x when 0s . Then:
0
0
(1 ) or (1 )
i
i i
i
x
x x t t
x
So that:
0 0 0
x y z
x y z
as per the streamlines.
Problem 2.5
(a) 2 2
16 10u x y v w y z
10 10
2
0 0
5 5
0 0
0 0
2
10 10
0 0
5 5
16,000
On 0 10, 0: 16
3
On 0 5, 10: 10 50
16,000
On10 0, 5: (16 5) 50
3
On 5 0, 0: 10 50
x y udx x dx
y x vdy dy
x y udx x dx
y x vdy dy
Then, adding the components around the counter-clockwise path gives:
50
(b) For the area specified, and 1z z
v u
x y
n e .
10 5
0 0
( 1)
A
dA dx dyω n

23. FLOW KINEMATICS
Page 2-5
50
A
dAω n
This is the same result that was obtained in (a), so that Eq. (2.5) is verified for this flow.
Problem 2.6
2 2 2 2
and
x y
u v
x y x y
1 1 1 1
1 1 1 1
1 1 1 1
2 2 2 21 1 1 1
( , 1) ( 1, ) ( , 1) ( 1, )
1 1 1 1
u x dx v y dy u x dx v y dy
xdx y dy xdx y dy
x y x y
In the foregoing equation, we note that there are two pairs of offsetting integrals. Hence:
0
Problem 2.7
(a) 2 2
9 2 10 2u x y v x w yz
11 1
2 3
1 1 1
( , 1) (9 2) [3 2 ] 2u x dx x dx x x
11 1
1 1 1
( 1, ) 10 [10 ] 20v y dy dy y
11 1
2 3
1 1 1
( , 1) (9 2) [3 2 ] 10u x dx x dx x x
11 1
1 1 1
( 1, ) ( 10) [ 10 ] 20v y dy dy y
Hence: 2 20 10 20 32du l
(b) 2
2 8x y z x z
w v u w v u
z
y z z x x y
ω e e e e e
Hence 50 8x zω e e on the plane 5z

24. FLOW KINEMATICS
Page 2-6
(c) For the plane 5z the unit normal is zn e . Hence:
1 1
1 1
8 32
A
dA dx dyω n
This agrees with the result obtained in (a) - as it should, since
A
d dAu l ω n
Problem 2.8
2 2 2 2
and
y x
u v
x y x y
1 1 1 1
1 1 1 1
1 1 1 1
2 2 2 21 1 1 1
1
1 1
121
(a) ( , 1) ( 1, ) ( , 1) ( 1, )
1 1 1 1
4 4[tan ]
1
u x dx v y dy u x dx v y dy
dx dy xdx dy
x y x y
d
2
2 2
2 2 2 2 2 2 2 2 2 2
(b)
1 2 1 2
( ) ( ) ( ) ( )
v u
x y
x y
x y x y x y x y
0 provided and 0x y
2 2 2 2 2 2
2 2
(c) and
( ) ( )
u x y v x y
x x y y x y
0 provided and 0x yu

25. FLOW KINEMATICS
Page 2-7
Problem 2.9
;u y v x
(a)
1 1 1 1
1 1 1 1
d ( ) ( )dx dy dx dyu
1 1 1 1
1 1 1 1
2 2 2 2
[ ] [ ] [ ] [ ]y yx x
4( )
(b) ( )
A
v u
ndA dxdy dxdy
x y
4( )
A
ndA
(c) and
dx dy
y x
ds ds
or
dy x
y dy xdx
dx y
2 2 2
2 2 2
y x c
2 2 2
x y c
(d) 2 2 2
1 and 1 x y c where andu y v x .
But x = 1 when y = 0 so that c 2
= 1. Therefore;
2 2
1x y
(e) 2 2 2
1 x y c where andu y v x .
But x = 0 when y = 0 so that c = 0. Therefore;
y x

26. FLOW KINEMATICS
Page 2-8
Problem 2.10
The vorticity vector will be in the z direction and its magnitude will be:
1 1
( , ) ( )
u
R Ru
R R R
(a) 0 andRu u R
2
( ) ( ) 2
and 0
R
Ru R R
R R
u
( , ) 2R R
(b) 0 and
2
Ru u
R
( ) 0
2
and 0
R
Ru
R R
u
( , ) 0 provided 0R R

27. 3
SPECIAL FORMS OF THE
GOVERNING EQUATIONS

29. SPECIAL FORMS OF THE GOVERNING EQUATIONS
Page 3-1
Problem 3.1
From the definition of the enthalpy h we have /e h p   . Substituting this result into the
left side of the given relation gives the expression:
D Dh D p
Dt Dt Dt
Dh Dp p D
Dt Dt Dt

  




 
   
 
  
Substituting this result into the full version of the given relation produces the equation:
( )
Dh Dp p D
p k T
Dt Dt Dt



      u  
The term immediately to the left of the equality sign and the term immediately to the right of
it cancel each other by virtue of the continuity equation. Thus the equivalent expression
becomes:
( )
Dh Dp
k T
Dt Dt
     
Problem 3.2
From Appendix A we obtain the following vector identity:
   
 
2
1
2
1
2
1
2
1
2
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( )
 
 
  
      
u u u u u u
u u u u u u
u u u u u u
u u u u u



   
     
    
    
In the foregoing, use has been made of an identity from Appendix A for the term ( )u a  ,
in which a u . Also, use was made of an identity from Appendix A for the term
( )u  . For an incompressible fluid 0u so that:
  21
2
( ) ( ) ( )   u u u u u u
    

30. SPECIAL FORMA OF THE GOVERNING EQUATIONS
Page 3-2
Problem 3.3
From Bernoulli’s equation we have:
2
0
1 1
2 2
( )p p U   u u
In cylindrical coordinates, the velocity-squared term in this equation may be written as
follows:
2 2
2 22 2
2 2 2 2
2 2
4 2
2 2 2
4 2
4 2
2
4 2
1 cos 1 sin
1 2 (cos sin )
1 2 cos2
Ru u
a a
U U
R R
a a
U
R R
a a
U
R R

 
 

 
   
      
   
 
    
 
 
   
 
u u
Substituting this result into the Bernoulli equation gives the required expression for the
pressure at any location whose coordinates are ( , )R  :
4 2
2
0 4 2
1
2
( , ) 2 cos2
a a
p R p U
R R
  
 
   
 
Substituting R a in the foregoing expression produces the following value for the surface
pressure:
2
0
1
2
( , ) (1 2cos2 )Up a p    
Note that this result may be expressed as a non-dimensional pressure coefficient as follows:
0
21
2
( , )
2cos2 1p
p a p
C
U




  

31. 4
TWO-DIMENSIONAL POTENTIAL FLOWS

33. TWO-DIMENSIONAL POTENTIAL FLOWS
Page 4-1
Problem 4.1
cosz F
cos( )
cos cos( ) sin sin( )
cos cosh sin sinh
i
i i
x i y i
Therefore cos coshx
And sin sinhy
Eliminating using 2 2
cos sin 1
2 2
2 2
1
cosh sinh
x y
This is the equation of ellipses whose major and minor semi-axes are coshx and sinhy .
1
2
1
( ) cos
1
d
W z z
dz z
For x = 2 and y = 0, z = 2 and we get
1 1
0 and
3 3 3
i
W u v i.e
downwards velocity.
_____________________________________________________________________________
Problem 4.2
coshz F
cosh( )
cosh cosh( ) sinh sinh( )
cosh cos sinh sin
i
i i
x i y i
Therefore cosh cosx
And sinh siny
Eliminating using 2 2
cosh sinh 1
2 2
2 2
1
cos sin
x y
This is the equation of a family of hyperbolas whose semi-axes are cosx and siny .
1
2
1
( ) cosh
1
d
W z z
dz z
For x = 1/2 and y = 0, z = 1/2 so that
1 2 2
0 and
3 / 4 3 3
i
W u v i.e
upwards velocity.
_____________________________________________________________________________

34. TWO-DIMENSIONAL POTENTIAL FLOWS
Page 4-2
Problem 4.3
2 2
2 2 2
2 2 2 2 2 2 1
2 2 2
1
2 2 2
( ) log( ) log( )
2 2
log( )
2
log ( ) 2
2
2
log ( ) 4 tan
2 2
2
( , ) tan
2
m m
F z z i h z i h
m
z h
m
x h y i x y
m m x y
x h y x y i
x h y
m x y
x y
x h y
( ,0) 0 streamlinex
We can evaluate the velocity components from the complex velocity, then substitute the results
into Bernoulli's equation to get the pressure.
2 2
2 2
2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2
2 2 2 2 2 2
2 2 2 2 2
2 2 2
( ) log( )
2
2
2
( ) 2 ( ) 2
( ) 4 ( ) 4
( ) 2
( , )
( ) 4
( ) 2
and ( , )
( )
dF d m
W z z h
dz dz
m z
z h
m x x h y x y m y x h y x y
i
x h y x y x h y x y
m x x h y x y
u x y
x h y x y
m y x h y x y
v x y
x h y 2 2 2
4 x y
Hence 2 2
( ,0) and ( ,0) 0
m x
u x v x
x h
. Then from Bernoulli's equation:
2 2
0
1
2
( ,0) ( ,0) ( ,0)p x p u x v x
2 2
0 2 2 2 2
( ,0)
2 ( )
m x
p x p
x h
The force on the plate is obtained by integrating the pressure difference across it along the entire
surface. Noting that the pressure distribution is symmetric in x , we get:

35. TWO-DIMENSIONAL POTENTIAL FLOWS
Page 4-3
0
0
2 2
2 2 2 20
2 ( ,0)
( )
F p p x dx
m x dx
x h
2
i.e. (upwards )
4
m
F
h
Problem 4.4
( ) log( ) log( )
2 2 2
log
2 2
1 /
log ...where 1
2 1 / 2
1 /
log( ) log
2 2 1 / 2
log{(1 / )(1 / )}
2
log(1 2 / )
2
log(2 / )
2
i
i
m m m
F z z b z b i
m z b m
i
z b
m z b m
i e
z b
m m z b m
e i
z b
m
z b z b
m
z b
m
z b
m
z
b
In the expansions above it has been assumed that / 1z b . Now let andb m in such
a way that /m b U . This yields the result:
( )F z U z
This is the complex potential for a uniform flow of magnitude U in the positive x direction.

36. TWO-DIMENSIONAL POTENTIAL FLOWS
Page 4-4
Problem 4.5
2 2
2
2
2
2
2
( ) log( ) log( / ) log( ) log( / )
2 2 2 2 2
( )( / )
log
2 ( )( / ) 2
(1 / )(1 / )
log ...where 1
2 (1 / )(1 / ) 2
(1 / )(1
log( ) log
2 2
i
i
m m m m m
F z z b z a b z b z a b i
m z b z a b m
i
z b z a b
m z b a b z m
i e
z b a b z
m m z b a
e 2
2 2
2
2
/ )
(1 / )(1 / ) 2
log{(1 / )(1 / )(1 / )(1 / }
2
log(1 2 / 2 / )
2
log(2 / 2 / )
2
b z m
i
z b a b z
m
z b a b z z b a b z
m
z b a b z
m
z b a b z
In the foregoing expansions, it has been assumed that / 1z b . Now let andb m in
such a way that /m b U . This yields the result:
2
( )
a
F z U z
z
This is the complex potential for a uniform flow U past a circular cylinder of radius a .
Problem 4.6
2 2
2
2
2
2
2
( ) log( ) log( / ) log( / ) log( ) log
2 2 2 2 2
( )( / )
log
2 ( )( / )
( / 1)( / )
log
2 ( )( / )
log as
2 ( )( / )
m m m m m
F z z b z a b z a z b
m z b z a b
b z z a
m z b z a b
z z a
m z
b
z z a

37. TWO-DIMENSIONAL POTENTIAL FLOWS
Page 4-5
2 2
2 2
1
i.e. ( ) log
2 ( / ) / )
log[ ( / ) / )]
2
m
F z
z a a z
m
z a a z
On the surface of the circle of radius a this result becomes:
2
2 2
( ) log[ ( / ) )]
2
log[2 cos ( / )] log{ [( / ) 2 cos ]
2 2
i i i
i
m
F ae ae a ae
m m
a a e a a
2
log{( / ) 2 cos }
2 2
m m
a a i
For a , 2
( / ) 2a a so that 2
/ 2 cosa a and so / 2m . Therefore the
circle of radius a is a streamline. The required complex potential is given by:
2
( ) log
2 ( )( / )
m z
F z
z z a
The resulting flow field is illustrated below.
To determine the force acting on the cylinder, we calculate the complex velocity:

38. TWO-DIMENSIONAL POTENTIAL FLOWS
Page 4-6
2
1 1 1
( )
2 ( ) ( / )
m
W z
z z z a
2
2
2 2 2 2 2 2
1 1 1 2 2 2
( )
2 ( ) ( / ) ( ) ( / ) ( )( / )
m
W z
z z z a z z z z a z z a
Using this result and the Blasius integral law (for a contour that includes the cylinder, but
excludes the sink at z ) produces the following expression for the force that acts on the
cylinder:
2
2
2
2 2 2
2 2
2
( )
2
2 (residues of ( ) inside )
2
2 2 2 2
2 / / ( / )
2 /
4 ( / )
C
X iY i W z dz
i i W z C
m
a a a
m a
a
From this result, there is no force acting on the y-direction, and the force that acts in the x-
direction is:
2 2
2 2
2 ( )
m a
X
a
Problem 4.7
2
( ) ( )
2
2
2
2
( ) log log
2 2
log log
2 2 2
( )( / )
log since 1
2 ( )( / ) 2
(1 / )(1 / )
log
2 (1 /
i i
i i
i i
i
i i
i i
m m a
F z z be z e
b
m a m m
z e z be i
b
m z be z a be m
i e
z be z a be
m z be a bz e
z be 2
)(1 / ) 2i i
m
i
a bz e

39. TWO-DIMENSIONAL POTENTIAL FLOWS
Page 4-7
2 2
2
2
i.e. ( ) log (1 / )(1 / )(1 / )(1 / )
2
log 1 (2 / 2 / )
2
2 / 2 /
2
i i i i
i i
i i
m
F z z be a bz e z be a bz e
m
z be a bz e
m
z be a b z e
In the foregoing expansions, it has been assumed that / 1z b and 2
/ 1a bz . Now let
andb m in such a way that /m b U . Thus the following result is obtained:
2
( ) i ia
F z U z e e
z
Problem 4.8
2 2
2
2
2
2
2
( ) log( ) log( ) log( ) log( ) log
2 2 2 2 2
( )( / )
log
2 ( )( / )
(1 / )( / )
log
2 ( )( / )
( / )
log for
2 ( )
(
log
2
i i a i a i i
F z z b z z z b
b
i z b z a
b z z a b
i z b z a
z z a b
i z a
b
z z
i 2
2
/ )
( )
( / )
log log
2 ( ) 2
a z
z
i a z i
z
( )
( ) log log
2 ( ) 2
i
i
i
i ae i
F ae
ae
The last result gives the value of the complex potential on the surface of the cylinder i
z ae .
We now note that the argument of the first logarithm on the right side of this equation is of the
form i
R e , where 1R . Therefore, the imaginary part of the entire first term is zero, so that:
( , ) log constant
2
a
This confirms that the circle of radius a is a streamline, so that the required complex potential is:

40. TWO-DIMENSIONAL POTENTIAL FLOWS
Page 4-8
2
( / )
( ) log
2 ( )
i z a
F z
z z
The complex velocity for this flow field is defined by the following equation:
2
2
2
2 2 2 2 2 2
1 1 1
( )
2 ( / ) ( )
1 1 1 2 2 2
( )
2 ( / ) ( ) ( / )( ) ( / ) ( )
i
W z
z a z z
W z
z a z z z a z z z a z z
Using this result and the Blasius integral law (for a contour that includes the cylinder, but
excludes the vortex at z ), produces the following expression for the force that acts on the
cylinder:
2
2
2
2 2 2
2 2
2 2
( )
2 2
2 residues of ( ) inside
2
2 2 2 2
2 ( / ) ( / ) / ( )
2 ( )
C
i
X iY i W z dz
i i W z C
a l a a
a
a
Hence there is no force acting in the y-direction, and the force in the x-direction is:
2 2
2 2
2 ( )
a
X
a
Problem 4.9
2
( ) ( ) log
2
a i z
F z U z
z a
and
2
2
1
( )
2
a U i
W z U
z z

41. TWO-DIMENSIONAL POTENTIAL FLOWS
Page 4-9
2
2
2
2
2
2
2 2 4 2
2 2 2
2 4
2 2
3 2 2
2
2 2
2 2
( , )
2
and ( , )
2
( , ) ( ) ( )
2
( )
2 4
2
( , ) 2 2 cos2 sin
4
i i
i i
i i i i
i i
a U i
W R U e e
R R
a U i
W R U e e
R R
a U iU a U
W W R U e e e e
R R R
a U
i e e
R R
U
W W a U U
a a
Now use Bernoulli’s equation with the pressure far from the cylinder specified to be 0p . Then:
2
0
1
2
( , ) ( )p R p U W W
2
2 2
0 2 2
1
( , ) cos2 sin
2 8
U
p a p U U
a a
The upward force acting on the cylinder is defined by the following expression:
2
0
2
0
( , ) sin
sin sin
LF p a a d
U
a d
a
In the foregoing, it has been recognized that
2 2
0 0
sin sin cos 0m d m n d for all
values of and form n m . Hence the value of the lift force is:
LF U
Problem 4.10
(a) ( ) log log
2 2
m
F z z i z
log( ) log( )
2 2
i im
Re i Re
Hence
1
( , ) log
2
R m R
And
1
( , ) log
2
R m R

42. TWO-DIMENSIONAL POTENTIAL FLOWS
Page 4-10
(b)
1 1
( )
2 2
m
W z i
z z
Therefore ( )
2 2
i i
R
m
u iu e i e
R R
2
R
m
u
R
2
u
R
(c) From Bernoulli’s equation:
02 21
( )
2
R
pp
u u
Therefore
2 2
0
2 2 2 2
1
2 4 4
pp m
R R
2 2
0 2 2
1
( , ) ( )
8
p R p m
R
_____________________________________________________________________________
Problem 4.11
(a)
2 2
( ) 2
( ) ( )
a a
F z U z
z ih z ih
On y = 0:
2 2
( ) 2
( ) ( )
a a
F x U x
x ih x ih
2
2 2
2
2
( )
a x
U x
x h
Therefore
2
2 2
( ,0) 2 1
( )
a
x Ux
x h
Hence
2 2
22 2 2 2
2
( ,0) ( ,0) 2 1 2
a a x
u x x U Ux
x x h x h
2 2 2
22 2 2 2
2
( ,0) 2 1
a a x
u x U
x h x h
(b)
2 2 2 3
2 2 2 2 2 2 2 2 3
2 4 8
( ,0) 2
( ) ( ) ( )
u a x a x a x
x U
x x h x h x h

43. TWO-DIMENSIONAL POTENTIAL FLOWS
Page 4-11
2 2
2 2 2 2 2
4 4
3
( ) ( )
a Ux x
x h x h
Then the maximum/minimum occurs when x = 0 or when
2
2 2
4
3 0
( )
x
x h
; that is, when
2 2
3x h .
Hence
2
max 2
( ,0) 2 1
a
u x U
h
at x = 0
And
2
min 2
( ,0) 2 1
8
a
u x U
h
at 3x h
(c) From Bernoulli’s equation:
2 2( ,0) 1 1
( ,0) (2 )
2 2
opp x
u x U
So that 2 21
( ,0) 2 ( ,0)
2
op x p U u x
But from (b):
2
22 2 2 2 2 2
2 2 2
22 2 2 2 22 2
2 ( )
( ,0) 4 1 4 1
( )
a a x a h x
u x U U
x h x hx h
Therefore:
2
2 2 2
2 2
22 2
( )
( ,0) 2 2 1o
a h x
p x p U U
h x
_____________________________________________________________________________
Problem 4.12
1 1
2 2
1 1
2 2 3
(i) ( ) log( ) log( )
2 2
log( ) log( ) log
2 2 2
i i
i i
m m
F z z ae z ae
m m m
z ae z ae z
On the circle of radius , i
a z ae so that:

44. TWO-DIMENSIONAL POTENTIAL FLOWS
Page 4-12
1 1
2 2
1 1
2 2
1 1
2 2 3
1 2
2 32
( , ) log ( ) log ( )
2 2
log ( ) log ( ) log( )
2 2 2
log ( )
2
log ( ) log(
2 2
i ii i
i ii i i
i ii i i
i ii i i
m m
F a a e e a e e
m m m
a e e a e e ae
m
a e e e e e
m m
a e e e e e a
1 1 1
1
2 2 2 3 3
2
)
log 2(cos cos ) log
2 2
log 2(cos cos ) log log
2 2 2 2
i
e
m m m
a i
m m m m m
a i a i
From the imaginary part of the last equality we deduce the result:
1 2 3( , ) ( )
2
a m m m
Then the value of 3m that makes the circle of radius a a streamline is:
3 1 2m m m
(ii) Substituting the last result into the expression for ( )F z and differentiating with respect to z
gives:
1 1 2
1 2
2
1 1 1 1 1 1
( )
2 2i i i i
m m
W z
z z ae zz ae z ae z ae
On the surface of the circle of radius , i
a z ae so that:
1 1 2 2
1 2
( ) ( ) ( ) ( )
1 1 1 1
( , ) 1 1
2 21 1 1 1
i i
i i i i
m m
W a e e
a ae e e e
Using the cylindrical representation of the complex velocity gives the following expressions
for the velocity components on the surface of the cylinder:

45. TWO-DIMENSIONAL POTENTIAL FLOWS
Page 4-13
1 1
2 2
( ) ( )
1
1 1
( ) ( )
1
2 2
1 1
1
2 2 2cos( ) 2 2cos( )
1 1
1
2 2 2cos( ) 2 2cos( )
i i
R
i i
m e e
u iu
a
m e e
a
1 1 1
1 1
2 2 2
2 2
( , ) 0
sin ( ) sin ( )
and ( , )
4 1 cos( ) 1 cos( )
sin ( ) sin ( )
4 1 cos( ) 1 cos( )
Ru a
m
u a
a
m
a
Then, since 2 2
Rq u u , it follows that the magnitude of the velocity on the surface of
the cylinder is:
1 2
1 1 2 2
1 1 1 1
2 2 2 2
( , ) cot ( ) cot ( ) cot ( ) cot ( )
4 4
m m
q a
a a
(iii)We first use the condition ( , ) 0S
dq
a
d
. This gives the result:
1 2 2
1 1
2 2 2
2 2
1 1 1 1
2 2 2 2
1 1 1 1
2 2 2 2
cosec ( ) cosec ( )
4
cosec ( ) cosec ( ) 0
4
m
a
m
a
2 2
1 1
2 1
2 2
2 2
1 1
2 2
1 1
2 2
cosec ( ) cosec ( )
cosec ( ) cosec ( )
S S
S S
m m
The condition
2
1/ 2
2
( , )S e
d q
a cU R
d
gives the following equation:
1 1 2 2
1/21 2
3 3 3 3
1 1 2 2
1 1 1 1
2 2 2 2
1 1 1 1
2 2 2 2
cos ( ) cos ( ) cos ( ) cos ( )
8 8sin ( ) sin ( ) sin ( ) sin ( )
S S S S
e
S S S S
m m
cU R
a a
________________________________________________________________________

46. TWO-DIMENSIONAL POTENTIAL FLOWS
Page 4-14
Problem 4.13
1
( 1)
1
hence ... for critical points
n
n
n
n
n n
c
z
n
d z c
d
c
That is, the critical points are located at c times the nth root of +1 in the plane. Hence the
critical points are located at:
2 /
0,1,2, ...,( 1)i m n
ce where m n
+ic
-c +c +c -c +c
-ic
n = 2 n = 3 n = 4
From the equation of the mapping function it follows that:
( 1)
1
( 1)
n
i i n
n
c
x i y e e
n
Hence, equating real and imaginary parts on each side of this equation:
1
1
cos cos( 1)
( 1)
sin sin ( 1)
( 1)
n
n
n
n
c
x n
n
c
y n
n
Using the relations 2 2 2
and tan /R x y y x we get:
2 2 2 2
1
2
2 2
2 2( 1)
2
(cos sin ) cos cos( 1) sin sin( 1)
( 1)
cos ( 1) sin ( 1)
( 1)
n
n
n
n
c
R n n
n
c
n n
n

47. TWO-DIMENSIONAL POTENTIAL FLOWS
Page 4-15
1
1
sin sin ( 1)
( 1)
tan
cos cos( 1)
( 1)
n
n
n
n
c
n
n
c
n
n
Hence the equations defining the surface in the z plane are
1/22
2
2 1
1 cos
( 1) ( 1)
sin ( 1)
( 1)
sin
tan tan
cos( 1)
( 1)
cos
n n
n
n
c c
R n
n n
c n
n
c n
n
Expanding the results obtained above for 1 gives:
1
1 cos
( 1)
sin
tan 1 tan
( 1) sin cos
n
n
R n
n
n
n
The object shape for 0.7, 3n is shown below.
y / ρ
x / ρ

48. TWO-DIMENSIONAL POTENTIAL FLOWS
Page 4-16
Problem 4.14
From the mapping function the parametric equations of the mapping are:
2
2
cos
sin
c
x
c
y
For the chosen system of units a circle is drawn in the plane. From this diagram, values of the
radius are obtained at the various values of the angle over the range 0 0
0 to 360 . The
corresponding values of andx y are then calculated from the parametric equations above. The
following diagrams were drawn using an EXCEL program to calculate the values of andx y and
to plot the results.
(a) SI Units (mm)
(b) English Units (inches)
Problem 4.15
In the following, is the angle through which the stagnation point must be rotated in order to
satisfy the Kutta condition, a is the radius of the circle that produces the airfoil, and L is the
length of the wing element.
(a) SI Units
The chord in Prob. 4.14 was 241 mm, so that all lengths will be magnified by the ratio
3.0/0.241 = 12.448.

49. TWO-DIMENSIONAL POTENTIAL FLOWS
Page 4-17
1 0
2 2
3
air
2
7.5
tan 6.582
60.0 5.0
12.448 (60.0 5.0) 7.5 0.8145
1.225 /
4 sin 293.3 /
1.225 250 293.3 1.0L
a mm m
kg m
U a m s
F U L N
4
8.982 10LF N
(b) English Units
The chord in Prob. 4.14 was 9.66 inches = 0.805 feet, so that all lengths will be magnified by
the ratio 9.0/0.805 = 11.18.
1 0
2 2
3
air
2
0.3
tan 6.582
2.4 0.2
11.18 (2.4 0.2) 0.3 2.438
0.002378 /
4 sin 2,634.3 /
(0.002378 32.2) 750 2,634.3 3.0L f
a ins ft
slug ft
U a ft s
F U L lb
5
4.538 10L fF lb
Problem 4.16
Consider a sector whose vertex is located at the origin in the z -plane (point A) and let the
corresponding point in the -plane be the origin (point a). Then, from the Schwarz-Christoffel
transformation:
1
1
1
( 0) n
n
dz
K
d
z n K
The constant of integration has been taken to be zero since 0z when 0. The scaling
constant K is undetermined in this case, and there is no loss of generality in specifying its value
to be such that 1nK . Then:
n
z

50. TWO-DIMENSIONAL POTENTIAL FLOWS
Page 4-18
Hence for a uniform flow of magnitude U in the -plane:
( ) n
F z U z
Problem 4.17
1/2
1/2 1 1/2
1/2
2 1/2
2 1/2 2 1/2
1 1
( 1)
( 1) ( 0) ( 1)
( 1)
1
( 1)
1 1
( 1) ( 1)
cosh sec
dz
K
d
K
K
z K A
When 0, 1z so that the constant A = 0. Also, when (1 ) , 1z i so that the
constant /K . Thus the equation of the mapping is:
1 1
cosh secz
The flow in the -plane is that of a source located at the origin. Since half of this flow will be in
each half-plane, the strength of the source in the -plane will be 2 U , so that the complex
potential will be:
( ) log
U
F
Problem 4.18
1 / /
( 0) ( 1) ( )
1 1
dz
K
d
K
Hence the differential equation of the mapping function is:

51. TWO-DIMENSIONAL POTENTIAL FLOWS
Page 4-19
21 1
r
ndz
K
d
The flow in the -plane is that of a source located at the origin. Since half of this flow will be in
each half-plane, the strength of the source will be 2 U H . Hence the complex potential will be:
( ) log
U H
F z
2
( )
1
r
n
dF dF d
W z
dz d dz
U H
K
2
i.e. ( )
1
r
nU H
W z
K
As the point D is approached, z while and ( )W z U . Hence from the foregoing
equation:
( ) 1
U H
W z U
K
H
K
As the point A is approached, z while 0 and ( ) /W z U H h. Hence:
2 2
( )
r r
n nU H U H
W z U
h K
2n
rH
h

52. TWO-DIMENSIONAL POTENTIAL FLOWS
Page 4-20
Problem 4.19
1 1/2 1/2
1/2
( 0) ( 1) ( )
1 1
dz
K
d
K
let 2
1
s
then
2
2
1
s
s
so that 2
1
1
1 s
and
2
2
( 1)
1
s
s
2
2
(1 )
( )
dz s
K
d s s
but 2 2
2 ( 1)
(1 )
d s
ds s
2 2
2 2
2( 1)
(1 )( )
1 1
2
(1 ) ( )
1 1 1 1
2
2(1 ) 2(1 ) 2 ( ) 2 ( )
dz dz d
K
ds d ds s s
K
s s
K
s s s s
1 1
log(1 ) log(1 ) log( ) log( )
1 1
log log
1
z K s s s s A
s s
K A
s s
At the location ,C so that 0s . Also, 0z , so that 0A . At the location , 1B so
that s . Also, ( )z i H h so that:
1
( )
( 1)
K H h

53. TWO-DIMENSIONAL POTENTIAL FLOWS
Page 4-21
1 1 1
( ) log log
1( 1)
s s
z H h
s s
In order to determine the constant , we specify the velocity at the location z to have the
value U. Then the source at z will have strength 2Uh , which will also be the strength of
the source located at 0. Then:
(2 )
( ) log
2
1
( )
U h
F
U h
W
1/2
( 1)
( ) ( )
( ) 1
d h
W z W U
dz H h
Then using the conditions discussed above at the location 0 produces the following result:
2
H
h
Thus the equation of the mapping becomes:
2
2
1 /
log log
1 /
( / )
where
1
H s h H h s
z
s H H h s
H h
s

55. 5
THREE-DIMENSIONAL POTENTIAL FLOWS

57. THREE-DIMENSIONAL POTENTIAL FLOWS
Page 5-1
Problem 5.1
From Appendix A, the vorticity vector in spherical coordinates is defined by:
sin
sin
r
r
r r
r
u r u r u
 
 

 

  
 
  
e e e
u  
For axisymmetric flows, the velocity component u will be zero and all derivatives with respect
to  will be zero. Thus two components of the vorticity vector will be zero, and the remaining
component is defined as follows:
2
2
2
( , ) sin ( ) sin
1 1
sin
sin
ru
r r r u r
r
r
r r
   

 

  

 
 
    
    
    
In the last equality, the definition of the Stokes stream function has been used from Eqs. (5.3a)
and (5.3b). Thus if the flow is irrotational, the equation to be satisfied by the Stokes stream
function is:
2
2
2
1
sin 0
sin
r
r
 

  
   
  
   
Problem 5.2
Equation (5.18) is:
2
2
2
1
sin 0
sin
r
r
 

  
   
  
   
From Eq. (5.5b) the stream function for a uniform flow is:
2 21
2
( , ) sinr Ur  
Then
2
2 2 2
2
sinr U r
r





And 2 21
sin sin
sin
U r

 
  
  
  
  
Hence 2 21
2
( , ) sinr Ur   is a solution.

58. THREE-DIMENSIONAL POTENTIAL FLOWS
Page 5-2
From Eq. (5.6b) the stream function for a source is:
( , ) (1 cos )
4
Q
r  

  
Then
2
2
2
0r
r



And
1
sin 0
sin


  
  
 
  
Hence ( , ) (1 cos )
4
Q
r  

   is a solution.
From Eq. (5.7b) the stream function for a doublet is:
2
( , ) sin
4
r
r

  

 
Then
2
2 2
2
sin
2
r
r r
 



 

And 21
sin sin
sin 2 r
 
 
   
  
 
  
Hence 2
( , ) sin
4
r
r

  

  is a solution.
Problem 5.3
Substituting the assumed form of solution into Eq. (5.18) and dividing the entire equation by the
product RT produces the following result:
2 2
2
sin 1
0
sin
r d R d dT
R dr T d d

  
 
  
 
Employing the usual argument of separable solutions, we now point out that since the first term
is a function of r only and the second term is a function of  only, the only way that the two
terms can add up to zero for all values of andr  is for each term to be constant. For
convenience, we choose the value of the constant for the term involving R to be ( 1)n n  . Then
the ordinary differential equation for R will be:
2
2
2
( 1) 0
d R
r n n
dr
  
This is an equi-dimensional ordinary differential equation, so that the solution will be of the
following form:
( ) m
R r Ar
Then it follows that ( 1) ( 1) 0m m n n   
The two possible solutions to this algebraic equation are:

59. THREE-DIMENSIONAL POTENTIAL FLOWS
Page 5-3
or ( 1)m n m n   
The second possibility leads to diverging values of the velocity as the radius r becomes large.
Thus for finite values of the velocity, the solution for R will be:
( ) n
n nR r A r 

The differential equation that is to be satisfied by T then becomes:
1
sin ( 1) 0
sin
d dT
n n T
d d

  
 
   
 
Let cos  be the new independent variable. Then the differential equation becomes:
2
2
2
(1 ) ( 1) 0
d T
n n T
d


   
Next introduce a new dependent variable that is defined by the relation 2 1/2
(1 )T    . From
this definition, the following derivatives are obtained:
2 1/2 2 1/2
2 2
2 1/2 2 1/2 2 2 3/2 2 1/2
2 2
(1 ) (1 )
(1 ) 2 (1 ) (1 ) (1 )
dT d
d d
d T d d
d d d

   
 
 
       
  

  
   
       
Thus, in terms of the new dependent variable  , the differential equation becomes:
2
2
2 2
1
(1 ) 2 ( 1) 0
1
d d
n n
d d
 
  
  
 
       
This is a special form of the Associated Legendre equation. The general form of the Associated
Legendre equation is:
2 2
2
2 2
(1 ) 2 ( 1) 0
1
d d m
n n
d d
 
  
  
 
       
The solution of this last equation, for any values of andm n, is:
( ) ( ) ( )
m m
mn mn n mn nB P C Q    
2 /2
2 /2
( )
where ( ) (1 )
( )
and ( ) (1 )
m
m nm
n m
m
m nm
n m
d P
P
d
d Q
Q
d

 


 

 
 

60. THREE-DIMENSIONAL POTENTIAL FLOWS
Page 5-4
In the foregoing expressions, and
m m
n nP Q are, respectively, the Associated Legendre functions
of the first and second kind of order m , while andn nP Q are, respectively, the Legendre
functions of the first and second kind. Then the equation derived here is the Associated
Legendre equation of order one; that is, 1m  . The Legendre functions of the second kind
diverge for values of 1   so that, in order to eliminate the possibility of infinitely large
velocities, the constants
m
nC must be taken to be zero. Thus the finite solutions to the given
differential equation, for any value of n , must be of the following form:
2 1/2
( )
( ) (1 )
ndP
d

  

 
Combining the elements of the solution we have, for any value of n :
2 1/2
( , ) ( )(1 ) ( )
where cos
n n nr A R r    
 
 

Substituting the foregoing results for ( ) and ( )n nR r   into the expression for the stream
function yields the result:
2
2
( )(1 )
( , )
sin
(cos )
n
n n
n nn
dP
r A
r d
d
A P
r d

 






   
This solution is valid for any value of the integer n , so that a more general solution will be
obtained by superimposing all such solutions. This produces the result:
1
sin
( , ) (cos )n n nn
n
d
r A P
r d

  



   
Problem 5.4
Substituting 0nA  for 1n  in the result obtained in the foregoing problem gives:
1 1
sin
( , ) (cos )
d
r A P
r d

  

   
But 1(cos ) cosP   so that the first term in the general solution gives the following result:
2
1
sin
( , )r A
r

   
This is the same as Eq. (5.7b) in which 1 / 4A   .

61. THREE-DIMENSIONAL POTENTIAL FLOWS
Page 5-5
Problem 5.5
Using the expression for the stream function for a doublet as given by Eq. (5.7b), and employing
the notation defined in Fig. 5.13, the following result is obtained:
2 2
*
( , ) sin sin
4 4
r
 
   
  
  
We now consider a point P that lies on the circle of radius r a . Then, referring to Fig. 5.13,
the following two identities follow from application of the sine rule:
sin ( ) sin
sin ( ) sin
a
a

  

  




Using these two results, the equation for the stream function on the circle of radius a becomes:
2 3
3 3
*sin
( , )
4
a
a
  
  
  
 
   
 
This result shows that the stream function will not be constant on r a unless:
3
* 
 

 
  
 
In order to evaluate the ratio of the lengths that appear in this result, we employ the cosine rule
on the triangles shown in Fig. 5.13 to obtain the following two identities:
2 2 2
4 3
2 2
2
2 cos
2 cos
a l al
a a
a
l l
 
 
  
  
Eliminating cos between these two equations gives the following results:
3
*
a
l
a
l


 

 
  
 

Substituting this last result into the expression for the stream function produces the following
result for the stream function for a sphere of radius a with a doublet of strength  located along
the flow axis at r l :
3
2 2
3
( , ) sin sin
4 4
a
r
l
 
   
   
  

62. THREE-DIMENSIONAL POTENTIAL FLOWS
Page 5-6
Using Eq. (5.7a) for the velocity potential yields the following result for the two doublets:
2 2
*
( , ) cos cos
4 4
r
 
   
  
 
Using the result obtained above relating the strengths of the two doublets produces the following
expression for the velocity potential for a sphere of radius a with a doublet of strength 
located along the flow axis at r l :
3
2 3 2
( , ) cos cos
4 4
a
r
l
 
   
   
 
Problem 5.6
From Eq. (5.14c) the force due to a doublet of strength  is given by:
(5.6.1)
i
x
 

 

u
F
where iu is the velocity induced by all singularities associated with the flow field, except that of
the doublet in question. Then, from the results obtained in the previous problem, the appropriate
velocity potential, due to the doublet located at 2
/x a l , will be:
3
3 2
( , ) cos
4
a
r
l

  
 
 
But on the x -axis, for 2
/x a l , we have the following values:
2
0 ( / )and x a l   
Then along the x -axis, the appropriate velocity potential is:
3
3 2 2
3
3 2 3
3
3 2 4
3
2 2 4
( ,0)
4 ( / )
( ,0) ( ,0)
2 ( / )
3
and ( ,0)
2 ( / )
3
( ,0)
2 ( )
i x x
i
x
i
x
a
x
l x a l
a
x x
x l x a l
a
x
x l x a l
a l
l
x l a



 





 


 
 

 
 

 
 
u e e
u
e
u
e


Substituting this last result into Eq. (5.6.1) gives the following value for the force:
3
2 2 4
3
2 ( )
x
a l
l a
 



F e

63. THREE-DIMENSIONAL POTENTIAL FLOWS
Page 5-7
Problem 5.7
Integrating the partial differential equation for ( , )r t once with respect to r gives:
2
( )r f t
r



In the foregoing, ( )f t is some function of time. Applying the second of the given boundary
conditions shows that the function ( )f t has the following value:
2
( )f t R R
Thus the radial velocity in the fluid at any distance r from the sphere at any time t will be:
2
2
( , )
R R
r t
r r



Integrating the foregoing equation with respect to r yields the result:
2
( , ) ( )
R R
r t g t
r
   
where ( )g t is some function of time. Since the velocity potential  must be a constant, at most,
for large values of the radius r , it follows that the function ( )g t must be zero. Then the value of
the velocity potential will be:
2
( , )
R R
r t
r
  
In order to establish an expression for the pressure, we employ Bernoulli’s equation in the form
given by Eq. (3.2c). Then, since the density is constant in this case, Bernoulli’s equation gives:
2
1
2
( )
p
F t
t r
 

  
   
  
Since the first and third terms on the left side of this equation are zero far from the sphere, and
given that the value of the pressure is 0p there, the value of the quantity ( )F t is 0( ) /F t p  .
Then, using the results obtained above, the Bernoulli equation becomes:
22 2 2
0
2
1
2
( 2 ) ( , ) pR R R R p r t R R
r r 
 
    
 
2 2 4 2
0
4
( , ) 2
2
pp r t R R RR R R
r r r 
   
Then on the surface of the sphere, where r R , this expression becomes:
0 23
2
( , ) pp r t
RR R
 
  

64. THREE-DIMENSIONAL POTENTIAL FLOWS
Page 5-8
At 0t  the foregoing expression becomes:
2 3/2
1/2
3
2
1
0 ( )
d
RR R R R
R dt
  
Integrating this equation once with respect to r produces the following result:
3/2 3/2
0 0constantR R R R  
3/2
0 0
3/2
3/2
3/2
0 0
hence
1
and
R RdR
dt R
dt R dR
R R
 
  
Evaluating the foregoing integrals between the limits of 0 and t for time, and 0 and 0R for the
radius R , we get the result:
0
0
2
5
R
t
R

Problem 5.8
Eq. (5.9b) defines the velocity potential for a uniform flow of magnitude U approaching a
sphere of radius a in the positive x -direction. If we replace U with U in this expression, we
will get the velocity approaching the sphere in the negative x -direction. Then, if we add a
uniform flow in the positive x -direction, the result will correspond to a sphere that is moving
with velocity U in an otherwise quiescent fluid. The resulting velocity potential is:
3
2
1
2
( , ) cos (5.8.1)
U a
r
r
   
In the foregoing equation, , andU r  are all considered to be functions of time. In order to
switch to coordinates andx R, where both of these coordinates do not vary with time, we use
the relations:
2 2 1/2
0 0( ) cos and [ ( ) ]x x r r R x x    
Substituting these expressions into Eq. (5.8.1) we get the following result:
03
2 2 3/2
0
1
2
( )
( , ) (5.8.2)
[ ( ) ]
x x
x R U a
R x x


 
 
In the foregoing, 0andU x are both considered to be functions of time, but all of the other
quantities are time-independent. To obtain an expression for the pressure, we employ
Bernoulli’s equation in the form defined by Eq. (3.2c) in which the quantity ( )F t is evaluated

65. THREE-DIMENSIONAL POTENTIAL FLOWS
Page 5-9
using the given pressure far from the body where temporal variations vanish, and where the
velocity components vanish. Thus the applicable form of Bernoulli’s equation is:
1
2
( , ) pp r
t
 
 

   

u u
It is easier to evaluate the first term in this equation using Eq. (5.8.2), rather than using Eq.
(5.8.1). We note that only 0andU x are functions of time, and that
0
and
xU
U U
t t

 
 
Then from Eq. (5.8.2) the following expression is obtained for the temporal derivative of the
velocity potential:
3 2 3
2
2 3
1 1
2 2
( , ) cos (1 3cos )
U a U a
r
t r r

  

   

The velocity-squared term in Bernoulli’s equation is readily obtained from Eq. (5.8.1), producing
the following result:
2 2
2 6
2 2
6
1
4
1
cos sin
r r
U a
r
 

 
    
     
    
 
  
 
u u
Substituting these two results into the Bernoulli equation produces the following expression for
the pressure at any point in the fluid:
3 2 3 2 6
2 2 2
2 3 6
1 1 1 1
2 2 2 4
( , ) cos (1 3cos ) (cos sin )
U a U a U a
p r p
r r r
  
         
The force that acts on the sphere will be in the positive x -direction and its value may be
obtained by integrating the pressure over an annular area of surface, ensuring that the x -
component of this product is evaluated. That is, the force on the sphere will be defined by:
2
0
2 ( , )sin cosF a p a d

     
Using the result obtained above for the pressure, its value on the surface will be:
2 2 21 1 1
2 2 4
( , ) cos (1 4cos sin )p a p Ua U         
Substituting this value of the surface pressure into the integral expression for the force acting on
the sphere shows that the only non-zero term will be:
3 2
0
sin cosF a U d

     
Evaluating this integral shows that the force acting on the sphere will be:
32
3
F a U 
Referring to Eq. (5.17), the foregoing result will be recognized as the apparent mass of the
sphere multiplied by the acceleration of the sphere. That is, this is the same result as would be

66. THREE-DIMENSIONAL POTENTIAL FLOWS
Page 5-10
obtained by replacing the fluid flow field with its apparent mass and considering this mass to
follow the sphere while obeying Newton’s second law of motion.
_____________________________________________________________________________

67. 6
SURFACE WAVES

69. SURFACE WAVES
Page 6-1
Problem 6.1
From Eq. (6.5a)
22
2
2 2
1 tanh
2
c h h
gh h gh
   
   
     
     
     
(6.1.1)
Let
2
2
2
, and
2
c
V S
gh h gh
 

 
  
Then Eq. (6.1.1) becomes: 2
2
1
1 tanh
S
V 
 
   
    
   
(6.1.2)
Then for 1 : 2
2
1
S S
V  
 
 
    
 
Hence for a minimum value of V:
2
2 1 0
dV S
V
d 
  
S  (6.1.3)
That is:
2
2 h gh
 
 

Substituting the results from Eq. (6.1.3) into Eq. (6.1.2) gives:
 2 1
1 1 tanhV S
S
 
   
 
That is
2 2
2
2 tanh
c gh
gh gh
 
 

_____________________________________________________________________________
Problem 6.2
Using a frame of reference that is moving with velocity c in the positive x -direction, the
quantity z ct should be replaced by z in our earlier results. Also, from the moving frame of
reference, there will be a uniform flow of magnitude c in the negative x -direction, so that this
component must be added to the solution. Hence, using Eq. (6.7c), the required complex
potential will be:
2
( , ) cos ( )
sinh (2 / )
c
F z t c z z i h
h
 
  
   
We expand the ratio of the two transcendental functions as follows:

70. SURFACE WAVES
Page 6-2
2
2 2 2 2 2
cos ( ) cos cosh sin sinh
sinh (2 / ) sinh (2 / )
2 2 2
cos coth sin
2 2
cos sin for 2 / 1
z
i
h
z h z h
z i h i
h h
z h z
i
z z
i h
e

    
    
   
  
  
 
 
 

 

 
  

Hence the deep-liquid version of the foregoing result is:
2
( , )
z
i
F z t c z c e




  
2
( )
2
( , ) ( )
2 2
( ) cos sin
i x i y
y
F z t i c x i y c e
x x
c x i y c e i




  
 

 
 
     
 
     
 
Hence the stream function is defined by the following expression:
2
2
( , ) sin
y
x
x y c y c e



 

  
When , 0y    . Hence from the foregoing expression:
2
2
sin
y
x
e



 


Problem 6.3
2 /
( , ) i z
F z t c z c e  
 
  
2 /
2 /
2
( ) 1
2
and ( ) 1
i z
i z
dF
W z c ic e
dz
W z c ic e
 
 






 
     
 

   
 
2
2 2 / 2 / 2 2 ( )/
2
2 2 4 /
2 2 2
hence ( ) 1
2 2
1 2 sin
i z i z i z z
y
WW z c i e i e e
c e
     
 
  
  
  
 
 
 
 
 
     
   
 
    
   

71. SURFACE WAVES
Page 6-3
Substituting this result into Bernoulli’s equation produces the following result:
2 2
2 2 / 2 4 / 2 21 1
2 2
4 2 2 2
1 sin 1y yp x P
c e e g y c      
  
     
     
            
        
Using this result on the free surface where andy p P  , and using Eq. (6.18a), gives:
2 2
2 2 4 / 2 21 1
2 2
4 2 2
1 1c e g c   
    
  
     
          
        
Solving this equation for 2
c gives:
2
2 2 2 2 4 /
2
(2 / ) (4 / ) (2 / )
g
c
e  

        

 
Expanding the foregoing result and noting that / /    gives:
2
4 /
2 2
2
4
1
/ 2
4
1 1
/ 2
1 (2 / )
g
c
e
g
g
 

    
 
    
 
    
 
    
 
  

 
  
 


     
 

  
For / 0   the foregoing result becomes:
2
2
g
c



This result confirms Eq. (6.3b). Also, for / 1  the same equation shows that:
2
2 2
/(2 )
1 (2 / )
g
c
 
  


The last result shows that the effect of finite amplitude is to increase the speed of the wave.
Problem 6.4
For a wave travelling at velocity c in the positive x -direction on a liquid of depth h , the
complex potential is:

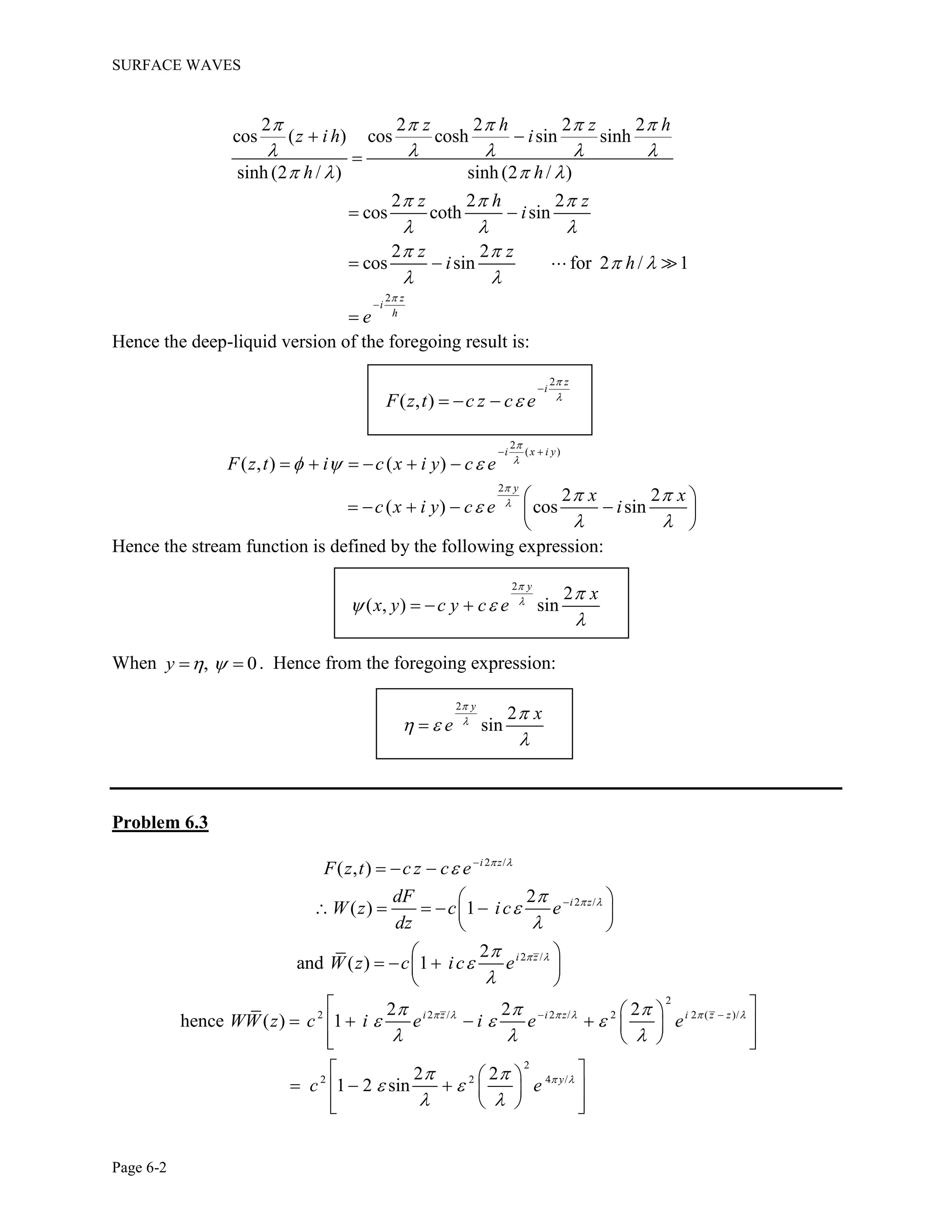
72. SURFACE WAVES
Page 6-4
2
( ) cos ( )
sinh (2 / )
c
F z z ct i h
h
 
  
   
We change the speed from c to U , and the liquid depth from h to H . At the same time, we
superimpose a uniform flow of magnitude U in the negative x -direction to account for the fact
that we are observing the flow from a frame of reference that is moving with the wave; that is,
with velocity U in the positive x -direction. Then the wave will appear to be stationary, and the
originally-quiescent liquid will appear to be approaching us in the negative x -direction. Also,
the distance z from the fixed origin will change such that z ct z  . The resulting complex
potential is:
2
( ) cos ( )
sinh (2 / )
2
( ) cos [ ( )]
sinh (2 / )
2 2 2 2
( ) cos cosh ( ) sin sinh ( )
sinh (2 / )
U
F z U z z i H
H
U
U x i y x i y H
H
U x x
U x i y y H i y H
H
 
  
 
  
    
     
   
     
 
        
Hence the stream function for the flow will be:
2 2
( , ) sin sinh ( )
sinh(2 / )
U x
x y U y y H
H
  

   
   
The relationship connecting the mean liquid speed, the liquid depth, and the wavelength of the
surface wave is given by Eq. (6.3a) in which c is replaced by U and the depth h is replaced by
H . This gives:
2
2
tanh
2
U H
g H H
 
 

Problem 6.5
Put U h  when 0 sin(2 / )y h x     in the expression obtained in Prob. 6.4 for the
stream function. This produces the following equation:
0 0
2
0 sinh [( ) sin 2 / ]
sinh(2 / )
U
U H h x
H
 
   
  
    
Consider 0 ( )H h  and solve this equation for the amplitude ratio, to get:
 0
sinh (2 / )
sinh 2 ( )/
1
cosh (2 / ) coth (2 / ) sinh (2 / )
H
H h
h H h
  
  
     





73. SURFACE WAVES
Page 6-5
But, from Prob. 6.4, 2
coth (2 / ) 2 /H U g    . Hence the expression for the amplitude ratio
becomes:
2
0
1
cosh(2 / ) ( / 2 ) sinh(2 / )h g U h

      


It may be observed that the amplitude ratio will be positive (so that the surface wave will be in
phase with the bottom surface) for values of U for which:
2
2
tanh
2
U g h
g h h
 
 

Conversely, the amplitude ratio will be negative (so that the surface wave will be out of phase
with the bottom surface) for values of U that reverse this inequality.
Problem 6.6
Superimposing the two given waves produces the following composite wave:
1 2
1 2
1
2
2 2
( , ) sin ( ) sin ( )x t x c t x c t
 
 
 
 
    
  
1 1
2 2
but sin sin 2cos ( ) sin ( )A B A B A B   
Hence the equation of the composite wave may be written in the following form:
1 2 1 2
1 2 1 2 1 2 1 2
1 1 1 1
( , ) cos sin
c c c c
x t x t x t   
       
          
                                    
If 1 2 1 2andc c    , the coefficient of time in the cosine component will be much smaller than
that of the sine component. Thus the cosine function will vary much more slowly with time than
the sine function. Hence the expression for ( , )x t may be thought of as being of the following
form:
1 2
1 2 1 2
1 1
( , ) ( , )sin
c c
x t A x t x t 
   
    
               
In the foregoing equation, the amplitude ( , )A x t varies slowly with time compared with the
frequency of the sine term.
Problem 6.7
(a) 2
0
1
2
V g dx

  

74. SURFACE WAVES
Page 6-6
2 2
0
1
2
2
sin ( )g x ct dx
 
 

 
   

Hence: 21
4
V g  
(b) From Eq. (6.7a):
2 2 2 2
( , ) cos ( ) sinh coth cosh
y h y
x y c x ct
   
 
   
 
    
 
2 2
( ,0) coth cos ( )
h
x c x ct
 
 
 
  
Also
2 2
( ,0) cos ( )x c x ct
y
  

 

  

Hence:
2
2 2 2
0
1
2
2 2 2 2
coth cos ( ) where tanh
2
h g h
T c x ct dx c
     
 
    
  
21
4
T g  
Problem 6.8
The linearized form of Bernoulli’s equation is:
( , , )
( , , ) ( )
p x y t
x y t g y F t
t



  

The function ( )F t may be considered to be incorporated into the velocity potential ( , , )x y t . In
addition, the pressure may be considered to be measured relative to the hydrostatic value, so that
the term g y may be considered to be incorporated into the pressure term. Thus the pressure
perturbation that is induced by the wave will be represented by:
2
( , , ) ( , , )
2 2 2 2 2
sin ( ) sinh coth cosh
p x y t x y t
t
y h y
c x ct


    
 
    

 

 
   
 
In the above, Eq. (6.7a) has been used for the velocity potential ( , , )x y t . From this same
equation we also evaluate:
2 2 2 2 2
( , , ) sin ( ) sinh coth cosh
y h y
x y t c x ct
x
     

    
  
   
  

75. SURFACE WAVES
Page 6-7
2 2
3 2 2
2
2
3 2 2
2
2
3 2 2
2
2 2 2 2 2
sin ( ) sinh coth cosh
2
cosh ( )
2 2
sin ( )
2
sinh
4
1 cosh ( )
1 2 2
sin ( )
22 sinh
y h y
p c x ct
x
y h
c x ct
h
y h
c x ct
h
     
 
    

   
 


   
 

    
     
    
 
  
    
   
 
 
   
    
   
 
Substituting this result into the expression for the work done gives:
0
2
3 2 2
2
4
sinh ( )
1 2 2 4
sin ( )
22 sinh
h
WD p dy
x
h y h
c x ct
h

 
   
 
 





 
   
    
   
  

Using Eq. (6.3a) to eliminate 2
c from the foregoing equation produces the result:
2 2
2 2 2
sinh cosh
1 2
sin ( )
2 22 sinh cosh
h h h
WD g c x ct
h h
  
    
 
 
 
 
   
 
 
2 21 2 2 /
sin ( ) 1
2 sinh (2 / )cosh (2 / )
h
WD g c x ct
h h
  
 
    
 
   
 
For deep liquids, the term inside the square brackets in the foregoing equation becomes unity.
Then the average work done will be:
/
ave
0
( )
c
WD WD dt

 
/
2 2
ave
0
2
1 2
i.e. ( ) sin ( )
2
1
4
c
WD g c x ct dt
g
 
 

  
 


In the above, the integration has been carried out over time corresponding to one complete cycle
of the wave train. This result shows that for deep liquids:
1
2
( ) ( )aveWD T V 

76. SURFACE WAVES
Page 6-8
Problem 6.9
Since the fluid motion is in the xy -plane only, the vorticity vector will lie in the z -plane and
will have the following magnitude:
2v u
x y
 
 
   
 
Hence from the given expression for the stream function:
2 2
( )k l  
The material derivative of the total vorticity is given by the following expression:
D
u v v
Dt t x y
t x
  

 

   
   
  
 
 
 
In the foregoing, the nonlinear terms have been neglected as being quadratically small. Then:
2 2
2 2
( )
( )( ) ( )
D
k l
Dt t x
k l i ik
 

  
  
  
 
  
2 2
( )
D
i k k l
Dt
  

     
From the foregoing result, the value of  that makes the material derivative of the total vorticity
equal to zero is:
2 2
( )
k
k l

 

Problem 6.10
The velocity potential in both regions of the flow must satisfy Laplace’s equation and the
solutions will be similar to those of section 6.12. However, the solution for 1 must be able to
satisfy the boundary condition at y   , namely, that / y  must vanish there. Thus the
exponential function in the solution for 1 should be replaced with the equivalent hyperbolic
function whose derivative with respect to y vanishes at y   . This means that the solution
will be of the following form:
2
( )
1 1
2 2
( )
2 2
2
0: ( , , ) cosh ( )
0 : ( , , )
i x t
i x t y
y x y t A e y
y x y t A e e



 

 

  



 
    
 

77. SURFACE WAVES
Page 6-9
Imposing the kinematic interface conditions given by Eqs. (6.16e) and (6.16f), with 1 0U  and
2U U , yields the following values for the constants:
1
2
2
sinh
( )
i
A
A i U
 
 

 
 
 
Using these values, the expressions for the two velocity potentials become:
2
( )
1
2 2
( )
2
2
cosh ( )
( , , )
2
sinh
( , , ) ( )
i x t
i x t y
y
x y t i e
x y t i U e e



 

 


  
 

  

 

 
 
Next, we impose the pressure condition at the interface between the two fluids. This condition is
defined by Eq. (6.16g), with 1 2 1 20, andU U U       . This results in the following
quadratic equation for  :
2 22
1 coth 2 0U U
 
 

 
    
 
Thus the coefficient of the time in the equation of the interface will be:
1/2 2
1 coth
2
1 coth
i
U
 

 




This result shows that  will have an imaginary part for all wavelengths  and all flow
velocities U , so that the interface will be unstable. The wavelength that makes the imaginary
part of  a maximum is 0  .
Problem 6.11
As in the last problem, we take the equation of the interface to be:
2
( )
( , )
i x t
x t e



 


The solution for the velocity potential in each flow region will be similar to that of section 6.12,
except that the y -dependence must be capable of satisfying the boundary conditions that
/ 0y   on both andy h y h   . Hence the velocity potentials will be of the following
form:

78. SURFACE WAVES
Page 6-10
2
( )
1 1
2
( )
2 2
2
( , , ) cosh ( )
2
( , , ) cosh ( )
i x ct
i x ct
x y t A e h y
x y t A e h y












 
 
Substituting these expressions into the kinematic conditions defined by Eqs. (6.16e) and (6.16f)
in which 1 2 0U U  , produces the following values for the constants:
1
2
2
sinh
2
sinh
i
A
h
i
A
h
 


 


 

Substituting these values into the expressions for the velocity potentials gives:
2
( )
1
2
( )
2
2
cosh ( )
( , , )
2
sinh
2
cosh ( )
( , , )
2
sinh
i x ct
i x ct
h y
x y t i e
h
h y
x y t i e
h





  



  





 


Next we impose the pressure condition at the interface, which is defined by Eq. (6.16g) with
1 2 0U U  . This gives, after dividing through by  , the following expression for  :
2 2
1 1 2 2
2 2 2 2
coth coth
h h
g g
   
     
   
   
Solving this equation for  gives the following result:
1 2
1 2
2
tanh
2
g h   

   
 
     
This shows that the interface is stable (i.e. the amplitude will decay with time) for 1 2  , but
that it is unstable (i.e. the amplitude will grow with time) for 1 2  .

79. 7
EXACT SOLUTIONS

81. EXACT SOLUTIONS
Page 7-1
Problem 7.1
The solution that will exist for large times will be that for flow between two parallel surfaces, as
defined by Eq. (7.1b). Then the solution for finite times will be of the following form:
*( , )
( , )
u y t y
u y t
U h
where
* 2 *
2
u u
t y
with *
( , ) 0u y
and * 1
1
2
( ,0) ( 1) sinn
n
y n y
u y
h n h
In the above, the velocity *
( , )u y has been made to vanish leaving the Couette flow solution
for large values of time. Also, the value of *
( ,0)u y has been made equal to the negative of the
Couette flow distribution so that the net value of the total velocity ( ,0)u y is zero. The Fourier
series for the saw-tooth value of *
( ,0)u y has been used to make the initial condition compatible
with the separable solution to the partial differential equation.
The solution for *
( , )u y t may now be obtained by separation of variables. The solution will be
trigonometric in y , to permit matching the initial condition at 0t , and it will be exponential in
time. Thus the solution becomes:
2
/* 1
1
2
( , ) ( 1) sinn h tn
n
n y
u y t e
n h
This expression satisfies the differential equation and the boundary conditions. Hence the
complete solution becomes:
2
/1
1
( , ) 2
( 1) sinn h tn
n
u y t y n y
e
U h n h
Problem 7.2
The partial differential equation and boundary conditions to be satisfied are:
2
2
1
1
for ( , )
2
( ,0) 1 sin
( , ) finite
n
n
u u
u y t
t y
y U n y
u y U
h n h
u y t

82. EXACT SOLUTIONS
Page 7-2
In the foregoing, the Fourier series representation for the saw-tooth velocity distribution that
exists at 0t has been deduced from Prob. 7.1.
The solution for ( , )u y t may be obtained by separation of variables. The solution will be
trigonometric in y , to permit matching the initial condition at 0t , and it will be exponential in
time. Also, we recall that the separation constants for both the andy t dependence must be
related to each other in such a way that they produce a solution to the partial differential
equation. Thus the solution becomes:
2 2
21
1
2
( , ) 1 sin
n
tn h
n
U n y
u y t e
n h
Problem 7.3
Consider the solution to consist of the velocity that exists for large values of the time t, plus a second
component of the solution. For large values of the time t the flow will be independent of time, and the
velocity, call it u1, will depend on y only. Hence the governing equation becomes:
2
1
2
0 2
d u
P
dy
Then: 2
1( )u y Py Ay B
1( 1) 0u P A B and 1( 1) 0u P A B
0 andA B P
2
1( ) (1 )u y P y
Substituting 1 2( , ) ( ) ( , )u y t u y u y t into the governing equation for 0t gives:
2 2
1 2 1 2
2 2
2
u u u u
P
t t y y
The first term on the LHS and the first and second terms on the RHS add up to zero, so that the equation
governing the second component of the solution is:
2
2 2
2
2
2where ( ,0) (1 )
u u
t y
u y P y

83. EXACT SOLUTIONS
Page 7-3
But the Fourier series for 2
2 2
1
2 4
(1 ) ( 1) cos
3
n
n
n
y n y
n
. Hence we look for a separation of
variables solution for 2 ( , )u y t of the form:
2 ( , ) ( ) cosu y t T t n y
Substituting this expression into the PDE for 2 ( , )u y t we get:
2 2dT
n T
dt
So that:
2 2
( ) n t
nT t C e
Therefore:
2 2
2
1
( , ) cos n t
n
n
u y t C n y e D
But 2
2 2 2
1
2 4
( ,0) (1 ) ( 1) cos
3
n
n
n
u y P y P n y
n
Therefore: 2 2
2 4
and ( 1)
3
n
nD P C P
n
Hence:
2 2
2
1
2 2
2
( , ) (1 ) cos
3
4
where ( 1)
n
n t
n
n
n
n
u y t P y P H n y e
H
n
_____________________________________________________________________________
Problem 7.4
Here: ( ); 0u u y v w
For this situation, continuity is identically satisfied. Hence, noting that the gravitational force is
defined by sin cos 0x y zg gf e e e it follows from the Navier-Stokes equations that the
equation to be solved for ( )u y is:
2
2
sin
d u g
dy
(a) (i) Integrating this equation twice gives
2
( ) sin
2
g y
u y Ay B
The conditions (0)u U and ( ) 0u h give and sin
2
gh U
B U A
h
Hence;
2
( ) 1 1 sin
2
y gh y y
u y U
h h h

84. EXACT SOLUTIONS
Page 7-4
(ii)
2
0 0
( ) 1 1 sin
2
h h y gh y y
Q u y dy U dy
h h h
3
sin
2 12
Uh gh
Q
(iii) 0Q 2
6
sin
U
gh
(b) (i) Here (0) and ( ) 0
du
u U h
dy
(for zero stress). Hence:
2
( ) 2 sin
2
gh y y
u y U
h h
(ii) Integrating:
3
sin
3
gh
Q Uh
(iii) 0Q 2
3
sin
U
gh
which is a smaller angle than in (b)
Problem 7.5
Using Eq. (7.2c) for the velocity distribution, we get the following expression for the volumetric
flow rate, EQ , for the elliptic pipe:
2 2 2 2 2 2
1 /
2 2 2 20 0
2 2
2 2
1
4 1
2
2
8
b a z b
E
dp a b y z
Q dz dy
dx a b a b
dp a b ab
dx a b
Denoting the flow area by and / byA ab b a , this equation may be written in the
following form:
2
2
2
2
2 2 2
1
(7.5.1)
4 1
1 1 2
4 1 (1 )
E
E
dp
Q A
dx
Q dp
A
dx
For a maximum flow rate with a given value of the area A , the derivative above must be zero.
This requires that 1, so that:
1
b
a

85. EXACT SOLUTIONS
Page 7-5
The velocity distribution for flow in a circular conduit is given by Eq. (7.2b). From this result
the volumetric flow rate CQ in a circular conduit will be:
2 2
0
4
2
1
( )2
4
2 4
1
(7.5.2)
8
a
C
dp
Q a R RdR
dx
dp a
dx
dp
A
dx
In the foregoing, the flow rate has been expressed as a function of the flow area 2
A a . From
Eqs. (7.4.1) and (7.4.2), the ratio of the two volumetric flow rates, for a common pressure
gradient and a common flow area, is:
2
2
1
E
C
Q
Q
Hence for 4 / 3 the flow ratio becomes:
24
0.96
25
E
C
Q
Q
Problem 7.6
The partial differential equation that is to be satisfied in this case is the following:
2 2
2 2
0
dp u u
dx y z
Then, substituting the assumed form of solution for the velocity ( , )u y z gives:
3
6
dp
b dx
Since this value is a constant, the assumed form of the solution is valid and the complete solution
becomes:
3
( , ) 3 3
6 2 3 3 2 3
dp b b b
u y z z z y z y
b dx
Problem 7.7
(a) 2
1
1
2
( ) 1 4( )u y A y

86. EXACT SOLUTIONS
Page 7-6
2
1 1
2
1
2
8 ( ) and 8
du d u
A y A
dy dy
Hence the differential equation is satisfied provided A = P so that a solution is:
2
1
1
2
( ) 1 4( )u y P y
(b) 2
1
sinh
( , ) sin
sinh
n
n
n z
u y z B n y
n
2 2
2 22 2 2 2
2 22 2
and
u u
n u n u
y z
Hence another solution is: 2
1
sinh
( , ) sin
sinh
n
n
n z
u y z B n y
n
(c) 3
1
sinh ( )
( , ) sin
sinh
n
n
n z
u y z C n y
n
2 2
3 32 2 2 2
3 32 2
and
u u
n u n u
y z
Hence another solution is: 3
1
sinh ( )
( , ) sin
sinh
n
n
n z
u y z C n y
n
(d) 2
1 1
1
2
sinh sinh ( )
( , ) 1 4( ) sin sin
sinh sinh
n n
n n
n z n z
u y z P y B n y C n y
n n
This expression satisfies the correct boundary conditions at 1y . At 0 andz z we have:
z = 0: 2
1
1
2
0 1 4( ) sinn
n
P y C n y
z = α: 2
1
1
2
0 1 4( ) sinn
n
P y B n y
The Fourier series for the bracketed term { } is the following:
21
2
1 4( )y = 3 3
1
16
sin where 1 ( 1)n
n n
n
K n x K
n
Hence matching the boundary expressions requires the following values for the constants Cn and Bn:
andn n n nC PK B PK
2
1 1
1
2
sinh sinh ( )
( , ) 1 4( ) sin sin
sinh sinh
n n
n n
n z n z
u y z P y P K n y P K n y
n n
_____________________________________________________________________________

87. EXACT SOLUTIONS
Page 7-7
Problem 7.8
The only non-zero component of velocity in this case will be ( , )u y z and this velocity
component will be the solution to the following reduced form of the Navier-Stokes equations:
2 2
2 2
0
u u
y z
with ( , ) 0u y
and
1
2
( ,0) [1 ( 1) ]sinn
n
n y
u y U U
n b
In the foregoing, the boundary condition on 0z has be written in terms of the Fourier series
for a square wave of height U . The solution to this problem may be obtained by separation of
variables. In this solution, the y -dependence will be trigonometric and the z -dependence will
be exponential. Hence, the solution will be:
1
2
( , ) [1 ( 1) ] sin
n z
n b
n
n y
u y t U e
n b
The volumetric flow rate Q may be evaluated by integrating the velocity to give:
0 0
1
2
2 20
1
2
1 ( 1) sin
2
1 ( 1)
n z
b
n b
n
n z
n b
n
n y
Q dz U e dy
n b
b
U e dz
n
Thus the volumetric flow rate past any vertical plane across the flow will be:
22
3 3
1
2
1 ( 1)n
n
Q U b
n
Problem 7.9
(a)
1 1d dw dp
R
R dR dR dz
Fluid #1:
2
1 1 1
1
1
( ) log
4
dp R
w R A R B
dz
Fluid #2:
2
2 2 2
2
1
( ) log
4
dp R
w R A R B
dz
The fact that 1( )w R should be finite when 0R requires that the constant 1 0A . Also,
matching the shear stresses at 1R R produces the following result:

88. EXACT SOLUTIONS
Page 7-8
1 2 1 1 2
1 2 2
1
0
2 2
dw dw R R Adp dp
A
dR dR dz dz R
Hence the expressions for the velocity profiles become:
2
1 1
1
1
( )
4
dp R
w R B
dz
2
2 2
2
1
( )
4
dp R
w R B
dz
The boundary conditions 1 1 2 1( ) ( )w R w R and 2 2( ) 0w R then give the results:
2 2
1 1
1 2
1 2
1 1
4 4
R Rdp dp
B B
dz dz
2
2
2
2
1
0
4
Rdp
B
dz
Therefore:
2
2
2
2
1
4
Rdp
B
dz
And: 2 2 2
1 2 1 1
2 1
1 1
( )
4
dp dp
B R R R
dz dz
Hence the velocity components are:
22 2 2 2
1 2 1 1
2 1
2 2
2 2
2
1
( ) ( ) ( )
4
1
( ) ( )
4
dp
w R R R R R
dz
dp
w R R R
dz
(b) From above:
22 2 2
1 2 1 1
2 1
1
(0) ( )
4
dp
w R R R
dz
22 2
1 2 1
2 1
1
(0) 1
4
dp
w R R
dz
__________________________________________________________________________
Problem 7.10
In the present case, 00 and 0i . Then, from Eq. (7.3a):
2 2
0 0
2 2
0
( )
i
i
R R
u R R
RR R

89. EXACT SOLUTIONS
Page 7-9
2 2
0
0 2 2 2
0
( )
1
2
( )
i
i
u
R R
R R
R R
R R R
In the foregoing, the shear stress has been evaluated using the formulae in Appendix C. Then,
if 0T is the torque acting on the fluid at 0R R , we have the result:
2
0 0 02 ( )T R R
If iT is the torque acting on the fluid at iR R , then the required torques are:
2 2
0
0 0 2 2
0
4
( )
i
i
i
R R
T T
R R
Problem 7.11
The velocity distribution is defined by Eq. (7.3a):
2 2
02 2
0 0 02 2 2
0
1
( ) ( ) ( )
( )
i
i i i
i
R R
u R R R R
R R R
Now let the outer radius become infinitely large in this expression; that is, let 0R . Then:
2
0 0( ) ( )
i
i
R
u R R
R
Next, bring the fluid far from the origin to rest by setting 0 0. This gives the result:
2
( )
i iR
u R
R
The complex potential for a line vortex of the given strength is:
2
( ) logi iF z i R z
Thus the complex velocity will be represented by the following expression:
2
( ) ( )
i ii i i
R
R
W Re u iu e i e
R
Thus the velocity resulting from the line vortex will be described by the following equation:
2
( )
i iR
u R
R
This is the same result as obtained for the rotating cylinder. Therefore, a line vortex may be
thought of as consisting of a very small cylinder rotating in an otherwise quiescent fluid.

90. EXACT SOLUTIONS
Page 7-10
Problem 7.12
The problem to be solved for the velocity ( , )u y t consists of the following partial differential
equation and boundary conditions:
2
2
(0, ) cos
( , ) 0
u u
t y
u t U nt
u h t
Following the procedure employed in section 7.5, we look for a solution to this problem of the
following form:
( , ) Re ( ) int
u y t w y e
In the foregoing, Re means the “real part of” as before. Substituting this assumed form of
solution into the partial differential equation produces the following ordinary differential
equation for ( )w y :
2
2
0
d w n
i w
dy
But
1
(1 )
2
i i
Hence the solution for ( )w y that satisfies the homogeneous boundary condition at y h is:
( ) sinh (1 ) ( )
2
n
w y A i h y
Then the solution for the velocity ( , )u y t will assume the following form:
( , ) Re sinh (1 ) ( )
2
i ntn
u y t A i h y e
Imposing the boundary condition at 0y on this solution indicates the following value for the
constant A :
sinh (1 )
2
U
A
n
i h
Thus the solution for the velocity ( , )u y t will be:
sinh (1 ) ( )
2
( , ) Re
sinh (1 )
2
int
n
i h y
u y t U e
n
i h
Although the real part of this equation may be evaluated explicitly, it will be left in the form
given above for brevity.

91. EXACT SOLUTIONS
Page 7-11
Problem 7.13
Using the definition of the Reynolds number NR , Eq. (7.6) becomes:
cosh (1 )
( , ) Re 1
cosh (1 )
N
x int
N
y
i R
P a
u y t i e
n i R
(a) For any value of NR , the following identity is valid:
cosh (1 ) cosh( )cos( ) sinh( )sin( )N N N N Ni R R R i R R
In particular, for 1NR , the following expansion is valid:
But cosh (1 ) (1 )(1 ) ( )( )
1
N N N
N
i R i R R
i R
Also
2
cosh (1 ) 1N N
y y
i R i R
a a
2
2
cosh (1 ) 1
Therefore
1cosh (1 )
1 1
N N
NN
N
y y
i R i R
a a
i Ri R
y
i R
a
Thus the expression for the velocity ( , )u y t becomes:
2
2
( , ) Re 1
1 cos
x int
N
x
N
P y
u y t i i R e
n a
P y
R nt
n a
That is, using the definition of the Reynolds number NR , we get the result:
2 2
2
( , ) 1 cos
2
xP a y
u y t nt
a
The solution obtained above corresponds to Couette flow between two parallel surfaces in
which the magnitude of the pressure is varying slowly with time. That is, the flow behaves
like Couette flow in which the magnitude of the pressure gradient is defined by the
instantaneous value of cosxP t .

92. EXACT SOLUTIONS
Page 7-12
(b) For andNR y a we get:
cosh (1 )
0
cosh (1 )
N
N
y
i R
a
i R
( , ) Re (1 )
x int
P
u y t i e
n
That is, the velocity distribution for large values of the parameter NR will be:
( , ) sin
xP
u y t nt
n
This solution corresponds to an inviscid flow in which the velocity responds to the pressure
gradient only. That is, the temporal acceleration of the fluid is equal to the applied pressure
gradient.
Problem 7.14
The partial differential equation to be solved and the assumed form of solution are:
where ( , ) ( )
2
and
R
t R R R
R t f
t
R
t
Then the following expressions are obtained for the various derivatives indicated:
1
2 2
1
2
1
2
f f
t t t t
f
R t t
R
R f f
R R t t t
In the foregoing, primes denote differentiation with respect to the variable . We now substitute
these expressions in the assumed form of solution. This produces the following ordinary
differential equation:
21
2
(1 ) 0f f f
Integrating this equation term by term, and using integration by parts where appropriate, gives:

93. EXACT SOLUTIONS
Page 7-13
21
2
( ) ( )f f d f f f d f d A
In the above, A is a constant of integration. Simplifying this equation gives the result:
21
2
f f A
For small but non-zero values of t , both f and its derivative f will be zero for all areas of the
fluid away from the origin. Thus the constant A must be zero. Then the solution becomes:
2
4
( )f Be
2
4
( , )
2
R
t
R t Be
t
In order to evaluate the constant of integration B , we observe that for small values of the time t
the total circulation in the fluid will be . Thus, from Eq. (2.5):
2
2
4
0
0
2
2
2
2
or 4 1
where
4
A
R
t
dA
Be R dR
t
B e d
R
t
ω n
The value of the definite integral is a half, so that the constant B must have the value 1/ 2B .
Then the solution for the vorticity distribution will be:
2
4
( , )
4
R
t
R t e
t
From Appendix A, the only non-zero component of the vorticity vector is defined as follows:
2
2
4
4
1
( )
4
2
R
t
R
t
Ru e
R R t
Ru e C
The constant of integration C may be evaluated by observing that 0 asu t , since the
vortex will be fully decayed for large values of the time. This gives the value / 2C so that
the velocity distribution will be defined as follows:
2
4
( , ) 1
2
R
t
u R t e
R

94. EXACT SOLUTIONS
Page 7-14
The pressure distribution may be evaluated from the radial component of the momentum
equations which, for the flow field under consideration, reduces to the following form:
2
1u p
R R
Hence the pressure distribution will be defined by the following integral:
2 2
2
4
0 2 3
1
( , ) 1
4
R
t
p R t p e dR
R
2 2
2
4 2
0 2 3 3 3
1 2 1
4
R R
t t
p e e dR
R R R
This result may be expressed in terms of the following exponential integral:
1
E( ) a x
ax e dx
x
2 2 3 3
log
1! 2 2! 3 3!
ax a x a x
x
In order to reduce the expression for ( , )p R t to the form of this standard integral we integrate
each of the integrals obtained above by parts as follows:
2
2
2 2
24 4
3 2
4 4
2
4
2
2
2 2
3 2
1 1
...where
2
1 1 1
2 8
1 1
E
2 8 4
1 1 1
and E
2 4 2
R
t t
t t
R
t
R R
t t
e dR e d R
R
e e d
t
R
e
R t t
R
e dR e
R R t t
Substituting these values into the expression for the pressure obtained earlier, produces the
following result:
2 2
2 2 2 2
2 4
0 2 2
( , ) 1 2 E E
8 2 2 4
R R
t t R R R
p R t p e e
R t t t
_____________________________________________________________________________
Problem 7.15
For the given velocity components, the left side of the continuity equation becomes:
1
( ) 2 2 0
z
R
u
Ru a a
R R z

95. EXACT SOLUTIONS
Page 7-15
That is, the continuity equation is satisfied for all values of the parameters anda K . For the
given velocity components, the R -component of the Navier-Stokes equations is:
2
2
2
2
3
2
2
3
1 1
1
i.e.
(7.15.1)
R R R
R
u u u up
u R
R R R R R R R
K p a a
a R
R R R R
p K
a R
R R
Similarly, the -component of the Navier-Stokes equations gives the result:
2
3 3
1 1
1
i.e.
0 (7.15.2)
R
R
u u u u up
u R
R R R R R R R
a K a K p K K
R R R R R
p
Finally, the z -component of the Navier-Stokes equations shows that:
2
2
2
2
1
1
i.e. 4 0
4 (7.15.3)
z z
z
u up
u
R z z
p
a z
z
p
a z
z
Eq. (7.15.2) shows that the pressure p is independent of . Then Eqs. (7.15.1) and (7.15.3)
give, respectively:
2 2 2
12
2 2
2
( , ) ( )
2 2
( , ) (2 ) ( )
K a R
p R z g z
R
p R z a z g R
Comparing these two expressions shows that the pressure distribution is defined by the following
equation:
2
2 2 2 2
0 2
( , ) 4
2
K
p R z p a R a z
R
Substituting the revised expressions for the velocity components into the Navier-Stokes
equations, as per above, leads to the following modified expressions for the pressure gradient:

96. EXACT SOLUTIONS
Page 7-16
2
2 2
3
2
( )
4
p K
f a R
R R
p K
R f f a K R f
R
p
a z
z
The first and last of these equations pose no new restrictions on the function f . However, the
right side of the middle equation must be zero since there is no -dependence in the flow. This
leads to the following differential equation for f :
2
1 1
0
1
i.e. 0
a
f f f
R R
d a
f f
dR R
Integrating the last equation and noting that 1 and 0 asf f R gives:
2
2
2
2
1
hence 1
and u 1
a R
a R
a a
f f
R
f C e
K
C e
R
Since the velocity u must be finite as 0R , we must choose the value of the constant in this
equation to be 1C . This gives the following expression for the function f :
2
2
1
a R
f e

97. 8
LOW-REYNOLDS-NUMBER
SOLUTIONS

99. LOW-REYNOLDS-NUMBER SOLUTIONS
Page 8-1
Problem 8.1
Eq. (8.8b) gives the expression for the pressure distribution in a fluid that is moving uniformly
past a fixed sphere. Using this result, and noting that cosx r  , we get the following value for
the pressure on the surface of the sphere:
3
( , ) cos
2
U
p a
a

  
This pressure distribution is symmetric about the flow axis so that it is sufficient to consider the
force acting on an annular element of surface whose area is:
2
2 sindS a d  
The force in the positive x -direction due to the pressure distribution around the sphere will have
the following value:
0
2
0
( , ) cos
3 sin cos
pF p a d
Ua d


  
    
 



The value of the integral in the last equation is 2/3 so that the following value is obtained for the
force, or drag, on the sphere due to the pressure distribution around it:
2pF Ua 
Eq. (8.8c) gives the value of the total drag on the sphere due to both shear effects and pressure
effects. Comparing the foregoing result with Eq. (8.8c) leads us to the conclusion that two-thirds
of the total drag in Stokes flow is due to shear effects, and one-third is due to the distribution of
pressure around the surface.
Problem 8.2
For a liquid drop the boundary conditions that will exist at the interface between the outer flow
and the inner flow will be the following:
( , ) ( , ) 0 (8.2.1 )
( , ) ( , ) (8.2.1 )
( , ) ( , ) (8.2.1 )
r r
r r
u a u a a
u a u a b
a a c
 
 
 
 
   
 


where ( , )
r
r
u u
r r
r r r



  

 
  
  
In the foregoing equation, the variables associated with the inner flow are indicated with a
primed superscript.
The outer flow will have the same general form as for a rigid sphere, but the boundary conditions
indicated above will replace the ones used previously. Then the general solution for the outer

100. LOW-REYNOLDS-NUMBER SOLUTIONS
Page 8-2
flow will consist of the superposition of a uniform flow, a doublet, and a stokeslet. This gives
the following values for the velocity and the pressure:
3 4 2
3 4 2
3
1 1
3
1 1 3
2
x x r x r
x r
x x
U A c
r r r r
x x
U A c A c
r r r r
x
p c
r

   
       
   
   
        
   

u e e e e e
e e
In order to facilitate the imposition of the boundary condition defined by Eq. (8.2.1a), we use the
relationship connecting Cartesian and spherical coordinate systems as follows:
cos sinx r   e e e
Then the velocity vector for the outer flow may be written as flows:
3 3
2 2 1 1
cos sinrU A c U A c
r r r r
 
   
        
   
u e e
The first component on the right side of this equation must vanish on the surface r a by virtue
of the boundary condition (8.2.1a). This requires that the strength of the doublet is:
3
2
2
a
A U c
a
 
  
 
Then the outer flow will be described by the following equations:
3 2
3 2
3 2
3 2
2
2
1 cos 1 cos (8.2.2 )
1
1 sin 1 sin (8.2.2 )
2
1
2 cos (8.2.2 )
r
a a
u U c a
r r r
a a
u U c b
r r r
p c c
r

 
 
 
   
      
   
   
       
   

The inner flow may be defined by solving the Stokes equations using the given form for the
pressure distribution. This is most easily done through use of the stream function formulation, as
follows. We use the following identity, valid for any Stokes flow, to give:
2
2
( ) ( )
1
p

    
    
u u u
u
   
   
Applying this result to the inner flow for which p KU x  , we get:
cos sinx rKU KU KU       e e e 
Thus the magnitude of the vorticity must be given by the following expression:

101. LOW-REYNOLDS-NUMBER SOLUTIONS
Page 8-3
1
2
sinKUr    e
This makes
1
2
0 and sinr KUr          . Then:
1 1
( sin ) ( )
sin
cos sin ...as required.
r
r
r
r r r
KU KU
  

  
 
 
 
  
 
  
e e
e e
 
Then, from the definition of the vorticity in terms of the velocity components, this result requires
that the following equation be satisfied:
1
2
1 1
( ) sin
ru
ru KUr
r r r
 

    
 
We now introduce the Stokes stream function as defined by Eqs. (5.3a) and (5.3b). This
produces the following partial differential equation to be satisfied:
2
2 2
2 2
1
2
sin 1
sin
sin
KU r
r r
  

  
    
  
   
A separable solution to this equation of the following form is sought:
2
( , ) ( ) sinr U R r   
Substitution of this assumed form of solution leads to the following ordinary differential
equation that is to be satisfied by ( )R r :
2
2
2 2
1
2
2
d R R
K r
dr r
 
The particular solution to this differential equation is 4
/ 20Kr and the complementary solution
will be of the form n
r since the homogeneous equation is equi-dimensional. Substitution of
n
R r reveals that 2 or 1n n   , so that the complete solution is:
4 2
4 2 2
2
3
2
3
1
( )
20
1
( , ) sin
20
1 2
hence ( , ) 2 cos
10
1
and ( , ) 2 sin
5
r
N
R r K r M r
r
N
r U K r M r
r
N
u r U K r M
r
N
u r U K r M
r

  
 
 
  
     
 
     
 
      
 

In the foregoing, , andK M N are constants of integration. Since the velocity components must
both be finite at 0r  , it follows that we must choose 0N  . Also, the radial component of
velocity must be zero on r a . This requires that 2
/ 20M K a  . Thus the velocity and
pressure in the inner flow will be defined as follows:

102. LOW-REYNOLDS-NUMBER SOLUTIONS
Page 8-4
2 2
2 2
1
( , ) ( ) cos (8.2.3 )
10
1
( , ) ( 2 ) sin (8.2.3 )
10
( , ) cos (8.2.3 )
ru r U K a r a
u r U K a r b
p r KU r c

 
 
  
   
  
 
The outer and inner flow fields, as defined by Eqs. (8.2.2) and (8.2.3), must now be matched at
the interface, r a . From the kinematic condition (8.2.1b) and the dynamic condition (8.2.1c)
we get, respectively:
2
2
1 2 3
10 2
3 6
3
10
U a K c U
a
U a K c U
a

 
 
   
In arriving at the latter equation, it should be noted that the second term in the expression for the
shear stress is zero since u is of the form ( ) sinf r  where ( )f a vanishes. Then, for this
particular velocity distribution, the shear stress is given by the following expression:
( , )r
r a
u
a r
r r

  

 
  
  
The solution to the two algebraic equations arising out of the boundary conditions is:
2
2
3
1 ( / )
3
4 1 ( / )
5 /
1 ( / )
U a
c
K
a
 
 
 
 

 




The force acting on the fluid due to the stokeslet is defined by Eq. (8.6c). Thus the force acting
on the liquid drop will be:
drop
2
3
8 ( )
1 ( / )
6
1 ( / )
F c
U a
 
 

 
 



The drag force acting on the solid sphere is given by Eq. (8.8c), so that:
drop
solid
2
3
1 ( / )
1 ( / )
F
F
 
 



Although not explicitly requested, the resulting velocity and pressure distributions outside and
inside the drop are defined by the following equations:

103. LOW-REYNOLDS-NUMBER SOLUTIONS
Page 8-5
3 2
3 2
3 2
3 2
2
3
2
3
1 /
3
( , ) 1 cos 1 cos
2 1 /
1 /
3
( , ) 1 sin 1 sin
2 4 1 /
r
a U a a
u r U
r r r
a U a a
u r U
r r r

 
  
 
 
  
 
   
         
   
          
2
2 2
2
2 2
2
2
2
3
1 /
3
( , ) cos
2 1 /
/
( , ) ( )cos
2 1 /
/
( , ) ( )sin
2 1 /
1
( , ) 5 cos
1 /
r
U a
p r
r
U
u r a r
a
U
u r a r
a
r
p r U
a

 
 
 
 
 
 
 
 
 
  
 

 

   

  

 

Problem 8.3
One way of verifying that the given expression is a solution to the Stokes equations is to first
convert it to a fixed-base coordinate system. Thus we use the following relation:
sin cos sin sin cos
sin sin cos
r x y z
r x z y
    
  
  
    
e e e e
e e e e
Then the value of the Laplacian of the velocity vector will be:
2
2 2
2 2 2 2 2
1 1 1
( ) sin ( ) ( )
sin sin
0
r x r x r xr r r r
r r r r r

    
       
                

u e e e e e e
Hence a valid solution to the Stokes equations is:
0
r xr
p
 

u e e
Consider a linear combination of the foregoing solution and the solution for a rotlet as defined by
Eq. (8.5a). Then the resulting velocity field will be defined as follows:
2
1
r x r xAr B
r
   u e e e e
The applicable boundary conditions for this case are:

104. LOW-REYNOLDS-NUMBER SOLUTIONS
Page 8-6
0 0 0...when
...when
r x
i i r x i
r r r
r r r
   
   
u e e
u e e
This leads to the following algebraic equations for the constants A and B :
3 3
0 0
3 3
0
3 3
0 0
3 3
0
( )
( )
( ) )
( )
i i
i
i i
i
r r
A
r r
r r
B
r r
 


  
 

These values give the following velocity and pressure distributions for the flow between the two
spheres:
3 3 3 3
0 0 0 0
3 3 3 3 2
0 0
( ) ( ) ) 1
( ) ( )
constant
i i i i
r x
i i
r r r r
r
rr r r r
p
      
   
   

u e e
Eq. (8.5c) defines the torque that acts on the fluid, and hence the torque that acts on the sphere.
The value is:
8 xB  M e
Thus, inserting the value obtained for the constant B we get:
3 3
0 0
3 3
0
( ) )
8
( )
i i
x
i
r r
r r
 
  


M e
If we let 0ir  in the foregoing results, the values of the velocity, the pressure and the torque
become:
0
constant
0
r xr
p
  


u e e
M
Problem 8.4
For the given pressure distribution and using the assumed velocity distribution, the following
result is obtained:
2
2
( )
t
t


 

 

 
    
 
u
u
    
Hence the partial differential equation to be satisfied by the function  is:

105. LOW-REYNOLDS-NUMBER SOLUTIONS
Page 8-7
2 1
0
t




  

The boundary conditions to be satisfied by the velocity on the surface of an oscillating sphere of
radius a , and also far from the sphere, are as follows:
( , ) cos ( ) (8.4.1 )
( , ) finite as (8.4.1 )
ra t a t a
r t r b
 
  
u e
u

In consideration of Eq. (8.4.1a) it is clear that the velocity, and the function  , will both be
functions of andr t only. Furthermore, the time dependence will be defined by the time
dependence of the sphere’s motion. However, the possibility of a phase lag exists in the r -
dependence. Then the partial differential equation to be solved for the function  will be:
2
2
1 1
0
where ( , ) Re{ ( ) }i t
r
r r r t
r t R r e 
 


  
  
   

Substituting the assumed form of solution into the partial differential equation gives:
2
2
1
0
d dR
r i R
r dr dr



  
 
This differential equation may be simplified by introducing a new dependent variable r R  .
Then the differential equation becomes:
2
2
0
d
i
dr



  
Thus the solution to the original differential equation is seen to be:
/ ( ) / ( )1
( ) i r a i r a
R r Ae Be
r
       
 
In order to satisfy the boundary condition (8.4.1b) we must choose 0B  . Hence the solution
for the function ( , )r t becomes:
/ ( )
/2 ( ) [ /2 ( )]
( , ) Re
Re
i r a i t
r a i r a
A
r t e e
r
A
e e
r
  
   
  
  
 
  
 
 
  
 
In the foregoing, we have used the fact that (1 )/ 2i i  . In terms of the function ( , )r t ,
the boundary condition (8.4.1a) is:
( , ) Re{ }i t
a t ae 
 
Imposing this boundary condition on the solution establishes the value for the constant A to be
2
A a . Then:
2
[ /2 ( )]/ ( )
( , ) Re i t r ar aa
r t e e
r
   
    
  
 
Then the velocity distribution in the fluid will be defined by the following expressions:

106. LOW-REYNOLDS-NUMBER SOLUTIONS
Page 8-8
2
/ ( )
where ( , ) cos[ / 2 ( )]r aa
r t e t r a
r
 

    
 
  
u  
Problem 8.5
In spherical coordinates, the vorticity vector and the Stokes stream function for any
axisymmetric flow are defined as follows:
2
1 1
( )
1
sin
1
sin
r
r
u
r u
r r r
u
r
u
r r
 



 


 
  
  




 

e
Substitution of the last two expressions into the first gives:
2
2 2
2
2
2
2 2
1 sin 1
sin sin
1
i.e.
sin
sin 1
where
sin
r r r
L
r
L
r r


  
   



  
    
    
    
 
   
   
   
e
e


The quantity 2
L in the foregoing is a linear, second-order differential operator that is similar to,
but not equal to, the Laplacian operator. We next take the curl of  twice and invoke standard
vector identities as follows:
2 2
2
2
2 2
2 2
2 2
1 1
( ) ( )
sin sin
1 sin 1
( ) ( )
sin sin
1
( )
sin
rL L
r r r
L L
r r r
L L
r



 
  

 
   


 
   
 
     
          
e e
e
e
 
  

The following vector identities, and the Stokes equations, are now used to show that the left side
of the last equation is zero:

107. LOW-REYNOLDS-NUMBER SOLUTIONS
Page 8-9
2
[ ( ) ]
)
0
p
     


u u
= (
     
 
That is, the partial differential equation that is to be satisfied by the Stokes stream function, for
any pressure distribution, is:
2 2
( ) 0L L  
2
2
2 2
sin 1
where
sin
L
r r

  
  
  
   
_____________________________________________________________________________
Problem 8.6
A solution to the partial differential equation obtained in Prob. 8.5 above is now sought in the
following form:
( , ) ( )r r f  
Substituting this assumed form of solution into the partial differential equation shows that:
4 2
3 4 2
1
2 0
d f d f
f
r dr dr
 
   
 
The general form of the solution to this equation is:
( ) sin cos sin cosf A B C D         
The boundary conditions that must be satisfied by this solution are the following:
( ,0) 0 (0) 0
1
( ,0) (0)
( , / 2) 0 ( / 2) 0
1
( , / 2) 0 ( / 2) 0
r f
r
r U f U
r
r f
r
r f
r




 

 


 


   


 


 





Imposing these boundary conditions leads to the following four algebraic equations that are to be
satisfied:

108. LOW-REYNOLDS-NUMBER SOLUTIONS
Page 8-10
0
0
2
0
2
B
A D U
A C
B C D



  
 
   
The solution to this set of equations is:
2
2
0
/ 2
( / 2) 1
1
( / 2) 1
A U
B
C U
D U



 





Then the corresponding solution for the stream function will be as follows:
2
2
( , ) sin sin cos
( / 2) 1 2 2
U
r r
 
      

  
     
    
The solution obtained above exhibits the following orders of magnitude:
Ur u U 
Hence the order of magnitude of the inertia terms and the viscous terms will be as follows:
inertia forces
2
r
r
u U
u
r r




viscous forces
2
2 2 2
ru U
r r





Hence Reynolds number,
inertia forces
viscous forces
N
U r
R


Since the Reynolds number must be small compared to unity, it follows that the radius r must
satisfy the following condition for the solution to be valid:
r
U



109. 9
BOUNDARY LAYERS

111. BOUNDARY LAYERS
Page 9-1
Problem 9.1
For andx    , the following expressions for the two first derivatives are obtained:
v
x x x
u
y y y
 
   
 
  
      
   
      
     
  
     
But the quantity h may be approximated as follows in a boundary layer:
21 1
2 2
h p p u      u u
Then, from the foregoing results, the following expressions are obtained:
2 2
2 2
(9.1.1)
0
1
(9.1.2)
and (9.1.3)
p h u
u
x x x
h h u u
v u u v
p h u
u
y y y
u h
y
u u h
y

 
   

 
 
  
 
  
   
   
   
  
  
  
 

 
 

 

Substituting Eqs. (9.1.1), (9.1.2) and (9.1.3) into the boundary layer approximation to the Navier-
Stokes equations gives:
2
2
2
2
1
1
u u p u
u v
x y x y
u u v h h v h u u u h
u uv u uv



           
   
   
   
         
         
         
Performing algebraic simplification to this equation produces the following result:
2
2
h h
u
 
 

 
This equation is of the same form as the one-dimensional heat conduction equation.
Problem 9.2
For flow over a flat surface the Blasius equation for ( )f  is, from Eq. (9.4a):
3 2
3 2
1
0 (9.2.1)
2
d f d f
f
d d 
 

112. BOUNDARY LAYERS
Page 9-2
(a) Consider ( ) ( ) where /f F f F d f d   . Then the following derivatives are obtained:
2
2
23 2 2
2
3 2 2
df
F
d
d f dF df dF dF
F
d d d df df
d f d dF df dF dF df d F dF d F
F F F F
d d df d df df d df df df

  
   

  
      
          
      
Substituting these expressions into Eq. (9.2.1) and simplifying, produces the following result:
22
2
1 1
0 (9.2.2)
2
d F dF f dF
df F df F df
 
   
 
(b) Consider 2
( ) ( ) where ( / )/ and /F f G G dF df f F f    . Then the following
derivatives are obtained:
 
2
2
2 3
1
2
2
2
dF
G f
df
d F d dG
f G
df df d
dG dF F
f G
d f df f
dG G
f G
d f f
dG
G G
d








 
  
 
 
   
 
 
   
 
  
Substituting these expressions into Eq. (9.2.2) and simplifying produces the following result,
which is a first-order ordinary differential equation, as required:
1
( 2 ) 1 0
2
dG G
G G
d

  
 
     
 
Problem 9.3
Starting with the given ordinary differential equation, we first multiply by the integrating factor
f , then we integrate, as follows:
2
1 ( ) 0f f   
2
( ) 0f f f f f      

113. BOUNDARY LAYERS
Page 9-3
hence 2 31 1
2 3
( ) ( )f f f A    
The constant of integration, A , may be evaluated by noting that along the centreline of the flow
the velocity gradient is zero due to symmetry. This leads to the following conditions:
( ) 1 as
( ) 0 as
f
f
 
 
   
   
Thus the value of the constant is 2/3A  and the differential equation beomes:
2 31 1 2
2 3 3
( ) ( )f f f    
We now let ( ) ( )G f  which reduces the differential equation to the following form:
2 31 1 2
2 3 3
( )G G G   
hence 32
3
2 3G G G   
so that
3
2
3 2 3
dG
d
G G
 
 
(1 )(1 )(2 )
(1 ) (2 )
dG
G G G
dG
G G

  

 
The foregoing equation may be integrated by making the following change of variables:
let 2
( ) ( ) 2F G  
2
2 2
then
3 (3 )
3 ( 3 ) 3 ( 3 )
dF
d
F
dF dF
F F
 

 
 
Integrating this equation and adding a constant of integration, B , gives the result:
2 1 1
( ) log( 3 ) log( 3 )
3 3 3
B F F      
2 ( )
2 ( )
1
hence
3 1
1
tanh ( )
2
B
B
F e
e
B








 
  
 
therefore ( ) 2 3 tanh
2
f B


 
    
 
The constant B may be evaluated from the boundary condition (0) 0f   . This gives:

114. BOUNDARY LAYERS
Page 9-4
2
tanh 1.146
32 2
( ) 2 3 tanh 1.146
2
B B
f


 
   
 
 
    
 

Solving this equation for ( )f  yields the result:
2
( ) 3tanh 1.146 2
2
f


 
    
 
Problem 9.4
From section 9.3, the equation to be satisfied by the stream function ( , )x y for the case of no
pressure gradient is:
2 2 3
2 3
(9.4.1)
y xdy x y y
    

    
 
    
A solution to this partial differential equation of the following form is sought:
1/3
2/3
( , ) 6 ( )
where ( , )
x y x f
y
x y
x
  
 


For this assumed form of solution, the following values are obtained for the various partial
derivatives that are required:
2/3 2 2/3
2 1/3
2
2 4/3 3 4/3
2
3 1
2
3
4 5/3
3
2 4
6
2 4
6
6
x f x f
x
x f
y
x f x f
x y
x f
y
x f
y

   

 

   

 

 
 

 



 





   
 






Substituting these results into Eq. (9.4.1) and simplifying produces the following ordinary
differential equation for ( )f  :
2
2 2( ) 0f f f f     (9.4.2)
The boundary conditions that are to be satisfied by the function ( )f  are the following:

115. BOUNDARY LAYERS
Page 9-5
( ,0) 0
( ,0) 0
( , ) 0 as
v x
u
x
y
u x y y




  
These boundary conditions impose the following conditions on the function ( )f  :
(0) 0 (9.4.3 )
(0) 0 (9.4.3 )
f a
f b

 
( ) 0 as (9.4.3 )f c    
Integrating Eq. (9.4.2) produces the following result, where A is the constant of integration:
2f f f A  
The boundary conditions (9.4.3a) and (9.4.3b) require that the constant 0A  . Then, integrating one
more time gives the result:
2 2
f f B  
In the foregoing, the constant of integration has been taken to be 2
B . Separating variables in the last
equation produces the following expression:
2 2
( )
d f
d
B f


This equation may be integrated to arrive at the following result:
( ) tanhf B B C  
In the foregoing equation, C is the constant of integration. Applying the boundary condition (9.4.3a)
shows that 0C  , so that the solution for the function ( )f  becomes:
( ) tanhf B B 
Thus the solution for the stream function becomes:
1/3
2/3
( , ) 6 tanh
y
x y B x B
x
   

  
 
The constant B may be evaluated if the mass flow rate in the jet is known. Then, for any given value of
the flow rate, the integral of the velocity across the jet must equal the specified value, and this
requirement determines the constant B .
Problem 9.5
2
1/3 2/3 1/31
and
3 2
dU dU k
U k x k x U x
dx dx
 
   
Hence the boundary layer equation becomes:

116. BOUNDARY LAYERS
Page 9-6
2 2 2 3
1/3
2 3
3
k
x
y x y x y y
    
    
  
     
We assume a solution of the following form:
1/3
3 2
( ) where
2 3
m k y
k x f
x
   

 
Now calculate the various derivatives that are required as follows:
13
2 3
m
k x f m f
x
 
      
  
1/3m
k x f
y
 


2
4/3 1 1
( )
3 3
m
k x f m f
x y

       
   
2
2/3
2
2
3
mk
k x f
y





3 2
1
3
2
3
mk
x f
y





Substitute these results into the B.L. equation and remove the multiplicative brackets:
2
2 2 5/3 2 2 5/3 2 2 5/3 2 2 5/3
2
1/3 2 1
1 1
( )
3 3 3
2
3 3
m m m m
m
k
k x f f m k x f x f f mk x f f
k
x k x f
    
 
           
 

The first and third terms cancel each other, and the quantity 2
k may be cancelled throughout the
equation. Hence the differential equation reduces to:
1 2 5/3 2 5/3 2 1/32 1 1
( ) 0
3 3 3
m m m
x f m x f f m x f x           
 
In order for a similarity solution to exist, all x dependence must be eliminated from this equation. That is,
the following powers of x must be zero:
5 1
1 2
3 3
m m    
These equations are satisfied for
2
3
m 
Substituting this value of m into the differential equation gives:
21 1
( ) 0
2 2
f f f f     

117. BOUNDARY LAYERS
Page 9-7
Problem 9.6
(a)
1/22 3
0 2
( ) ( ,0) ( ,0) (0)
u U
x x x f
y y x
 
   
  
    
   
1/2
0
21
2
( ) 2 (0)
2 (0)
x
x f
f
U x RU
 

 
  
 

But 2
( ) 0.166 ( ) 0.332f f         for 1
0
21
2
( ) 0.664
x
x
RU



(b)
1
( , ) ( ) ( )
2 2 x
U U
v x y f f f f
x x R
 
 

      

( , ) 1
( )
2 x
v x y
f f
U R
  
For , 1 and ( ) 1.721y f     
( ) ( 1.721) 1.721f        
( , ) 0.8605
x
v x y
U R
 

(c)
2 2 2
2 2 2z
v u
x y x y y
  

    
      
    
( )z
U
U f
x
 

 
____________________________________________________________________________________
Problem 9.7
Here
( , )u x y y
a b
U 
 
The two boundary conditions that must be satisfied by this velocity distribution are:

118. BOUNDARY LAYERS
Page 9-8
( ,0)
0 0
( , )
1 1
u x
a
U
u x
b
U

  
  
Hence the velocity distribution across the boundary layer is defined by the equation:
( , )
...where (9.7.1)
u x y y
U
 

 
From section 9.8, the momentum integral for flow over a flat surface is:
0
0
( )
d
u U u dy
dx
 

 
1 0
20
or 1 (9.7.2)
d u u
d
dx U U U

 

 
   
  

Using Eq. (9.7.1), we obtain the following values:
1
0 0
0
1 (1 )
6
and ( ,0)
u u
dy d
U U
u U
x
y
 
   

 

 
    
 

 

 
Substituting these values into Eq. (9.7.2) yields the following ordinary differential equation to be
solved for the boundary layer thickness  :
2
1
6
12
d
dx U
x
C
U
 
 
 

 
We take the thickness of the boundary layer to be zero when 0x  , which requires that the
constant of integration 0C  . Thus the boundary layer thickness will be defined by:
12 3.464
N N
x R R

 
The displacement thickness is defined by the following relation:
1
0 0
*
1 (1 )
2
u
dy d
U
 
   
 
     
 
 
This gives the following value for *
 :
*
3 1.732
N N
x R R

 
The momentum thickness is defined by the following relation:

119. BOUNDARY LAYERS
Page 9-9
1
0 0
1 (1 )
6
u u
dy d
U U
 
    
 
     
 
 
This gives the following value for  :
1 1 0.577
3 N N
x R R

 
Finally, the surface shear stress coefficient is defined by the following relation:
0
21
2
2 1
UU
 


Then, using the value obtained above for  we find:
0
21
2
1 1 0.577
3 N NR RU


 
These values compare favorably with those obtained in section 9.8, in spite of the crude velocity
profile that was used.
Problem 9.8
Here
2 3
( , )u x y y y y
a b c d
U   
   
      
   
The four boundary conditions that must be satisfied by this velocity distribution are:
2
2
( ,0) 0
( , )
( , )
0
( ,0)
0
u x
u x U
u x
y
u x
y










These conditions yield the following values for the constants , , anda b c d .
0, 3/ 2, 0, 1/ 2a b c d    
Hence the velocity distribution across the boundary layer is defined by the equation:
3( , ) 3 1
...where (9.8.1)
2 2
u x y y
U
  

  
From section 9.8, the momentum integral for flow over a flat surface is:

120. BOUNDARY LAYERS
Page 9-10
0
0
( )
d
u U u dy
dx
 

 
1 0
20
or 1 (9.8.2)
d u u
d
dx U U U

 

 
   
  

Using Eq. (9.8.1), we obtain the following values:
1
3 3
0 0
0
3 1 3 1
2 2 2 2
39
1 1
280
3
and ( ,0)
2
u u
dy d
U U
u U
x
y

      

 

    
         
    

 

 
Substituting these values into Eq. (9.8.2) yields the following ordinary differential equation to be
solved for the boundary layer thickness  :
2
39 3
280 2
39 3
560 2
d
dx U
x
C
U
 
 



 
We take the thickness of the boundary layer to be zero when 0x  , which requires that the
constant of integration 0C  . Thus the boundary layer thickness will be defined by:
280 1 4.641
13 N N
x R R

 
The displacement thickness is defined by the following relation:
1
3
0 0
* 3 1
2 2
3
1 (1 )
8
u
dy d
U

     
 
      
 
 
This gives the following value for *
 :
*
315 1 1.740
104 N N
x R R

 
The momentum thickness is defined by the following relation:
1
3 3
0 0
3 1 3 1
2 2 2 2
39
1 1
280
u u
dy d
U U

       
    
          
    
 
This gives the following value for  :
117 1 0.646
280 N N
x R R

 
Finally, the surface shear stress coefficient is defined by the following relation:

121. BOUNDARY LAYERS
Page 9-11
0
21
2
3 1
UU
 


Then, using the value obtained above for  we find:
0
21
2
117 1 0.646
280 N NR RU


 
Problem 9.9
( , )
Here sin
2
sin ...where
2
u x y y
U
y



 

 
  
 
 
Then 0
( ,0)
2
u x U
y
 
 


 

Substituting these values into the momentum integral yields the following ordinary differential
equation to be solved for the boundary layer thickness  :
2 1
2 2
1 2 1
2 2 2
d
dx U
x
C
U
  
  
 


  
 

   
 

We take the thickness of the boundary layer to be zero when 0x  , which requires that the
constant of integration 0C  . Thus the boundary layer thickness will be defined by:
2 1 4.795
4 N N
x R R



 

The displacement thickness is defined by the following relation:
1
0 0
* 2 2
1 (1 sin ) 1
u
dy d
U

    
 
   
        
   
 
This gives the following value for *
 :
*
2 1 1.743
( 2)
4 N N
x R R



  

The momentum thickness is defined by the following relation:

122. BOUNDARY LAYERS
Page 9-12
1
0 0
2 2 1
1 sin (1 sin )
2
u u
dy d
U U

     
 
   
        
   
 
This gives the following value for  :
4 1 0.655
2 N N
x R R
 
 
Finally, the surface shear stress coefficient is defined by the following relation:
0
21
2
1
UU
 


Then, using the value obtained above for  we find:
0
21
2
4 1 0.655
2 N NR RU
 


 
Problem 9.10
1
y
y
u
e
U
u
U e
y








 




and 0 ( ,0)
u U
x
y
 
 


 

Then the value of the momentum integral becomes:
 
 
1
0 0
2
1 1
1 2
2
u u
dy e e d
U U
e e

 
 
 


 
 
 
   
 
  
 
Hence  21
1 2
2
d
e e
d x
   
 
 
  
Therefore
2
2
1 2
x
Ue e 
 

 

 
(taking the constant of integration to be zero)
2
2 1
1 2 N
x Re e 
 
 

 

123. BOUNDARY LAYERS
Page 9-13
Problem 9.11
0
1
1/7 1/7
0
1
8/7 9/7
0
1
(1 ) /
7 7
8 9
u u
dy
U U
d where y


     
  
 
  
 
  
 
   


7
72
 
Kármán integral 
1/42
0
02
where
44
d U
dx U U
  

 

   
 
1/4
7 1
72 44
d
dx U
 

 
  
 

1/4
1/4 18
77
d
dx U
 


  
 
1/4
5/44 18
constant
5 77
x
U



  
 
The constant of integration will be zero for 0 when 0x   . Hence:
4/5 1/5
4/545
154
x
U


  
    
  
4/5
1/5 1/5
N N
45 1 0.3737
154x R R
  
  
 
1/4 1/4 1/5
1/200
N1/4 1/4
2 N N
1
2
1 1 1 1 1 154
22 22 22 45
x
R
U R RU
 
 
    
       
    
1/5
0
1/5 1/5
2 N N
1
2
1 154 1 0.0581
22 45 R RU


 
  
 
7 7
72 72x x
 
   
4/5
1/5 1/5
N N
7 45 1 0.0363
72 154x R R
  
  
 

124. BOUNDARY LAYERS
Page 9-14
1
1
* 1/7 8/7
0 0
0
7
1 (1 )
8 8
u
dy d
U
 
      
   
            
 
4/5*
1/5 1/5
N N
1 45 1 0.0467
8 154x R R
  
  
 
Problem 9.12
From Eq. (9.12f), the momentum thickness is defined by the following equation:
2 2
2 0
5 5/6
6 0
5/6
0.47
( ) ( )
( )
0.47
0.2564
x
x
x U d
U x
A d
A x
x
A

  

 






Hence 7/6
0.5063
x Ax
 

Substituting this result into Eq. (9.12g) gives the following equation for the pressure gradient
parameter  :
22 2
37
0.04273
315 945 9072
dU
dx


  
    
 
There are three positive roots to this equation; 3.367, 21.326 and 32.829  . It follows from
Eq. (9.12b) that only the first of these values is physically reasonable. Then the following values
are obtained:
2
3.367
3
0.2719
10 120
37
0.1126
315 945 9072
 
 
  
 
  
   
 
Hence from Eq. (9.12d), the following value is obtained for the boundary layer thickness  :
7/6
4.4967
x Ax
 

The value of the displacement thickness *
 may now be determined from Eq. (9.12c):

125. BOUNDARY LAYERS
Page 9-15
7/6
*
1.2226
x Ax
 

Finally, the value of the surface shear stress 0 may be determined from Eq. (9.12e):
0
0
21
2
2
6
2
2
6
U
UU
 

 

 
  
 
 
  
 

0
7/6
21
2
1.1392
AxU
 


Problem 9.13
The only change to the boundary layer equations for this problem is to retain the body force term
in the form of the gravitational force. Thus the equations to be solved are:
0 (9.13.1)
u v
x y
 
 
 
2
2
(9.13.2)
u u dU u
u v U g
x y dx y

  
   
  
To obtain the momentum integral, we first add Eq. (9.13.1) to Eq.(9.13.2), then we integrate the
latter with respect to y between the limits 0 andy y   . Following the procedure that was
used in section 9.8, this produces the following result:
2
2
2
02
0 0
02
0 0 0
02
0 0 0 0
0
0 0
( ) ( )
( ) ( , )
( )
( ) ( )
dU u
u uv U g
x y dx y
dU
u dy U v x U dy g
x dx
u dU
u dy U dy U dy g
x x dx
d d dU dU
u dy Uudy udy U dy g
dx dx dx dx
d dU
u U u dy U u dy g
dx dx
 
  
   
 


 










  
   
  

   

 
   
 
    
    
 
  
   
 

126. BOUNDARY LAYERS
Page 9-16
That is
02 *
( )
d dU
U U g
dx dx

  

  
Using the definitions of the various thicknesses yields the following result:
0
2 2
* 1
(2 )
d dU g
dx U dx U U
 
 

   
Since the velocity profile in this problem is the same as that used in section 9.8 of the text, the
values of the various quantities of interest will be the same. Then:
2
0
0
0
*
2
2
1
15
1
1
3
( ,0)
2 2
u
U
u u
dy
U U
u
dy
U
u x U
y


 
 
 



 
 
   
 
 
   
 

 



Substituting these values into the momentum integral obtained above, leads to the following
ordinary differential equation to be satisfied by the boundary layer thickness  :
1/2
15
6 0
2
d
dx x xg
  

  
The solution to this ordinary differential equation is of the form m
C x  . Substituting this form
of solution into the equation shows that:
1/4
1 12
and
4 5 (2 )
m C
g

 
Then the solution for the boundary layer thickness  becomes:
3 1/4 3 1/4
12
1.5492
5 (2 ) (2 )x g x g x
  
 
Using the relationships connecting *
and  with  , the following values are obtained:

127. BOUNDARY LAYERS
Page 9-17
3 1/4 3 1/4
3 1/4 3 1/4
0
3 1/4 3 1/4
2
*
1
2
4
0.5164
15 (2 ) (2 )
4
0.2066
(2 ) (2 )375
20
2.582
3 (2 ) (2 )
x g x g x
x g x g x
g x g xU
  
  
  

 
 
 

129. 10
BUOYANCY-DRIVEN FLOWS

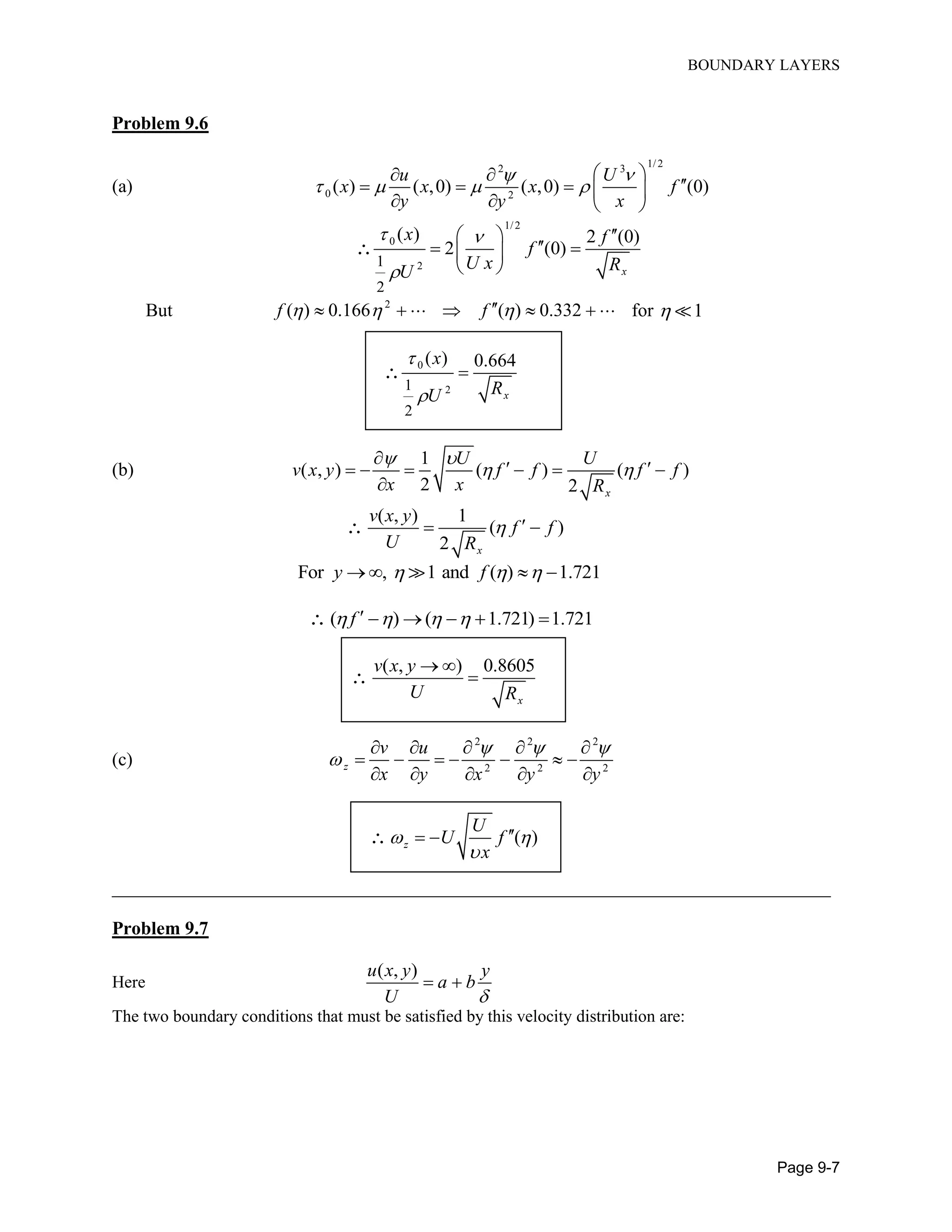
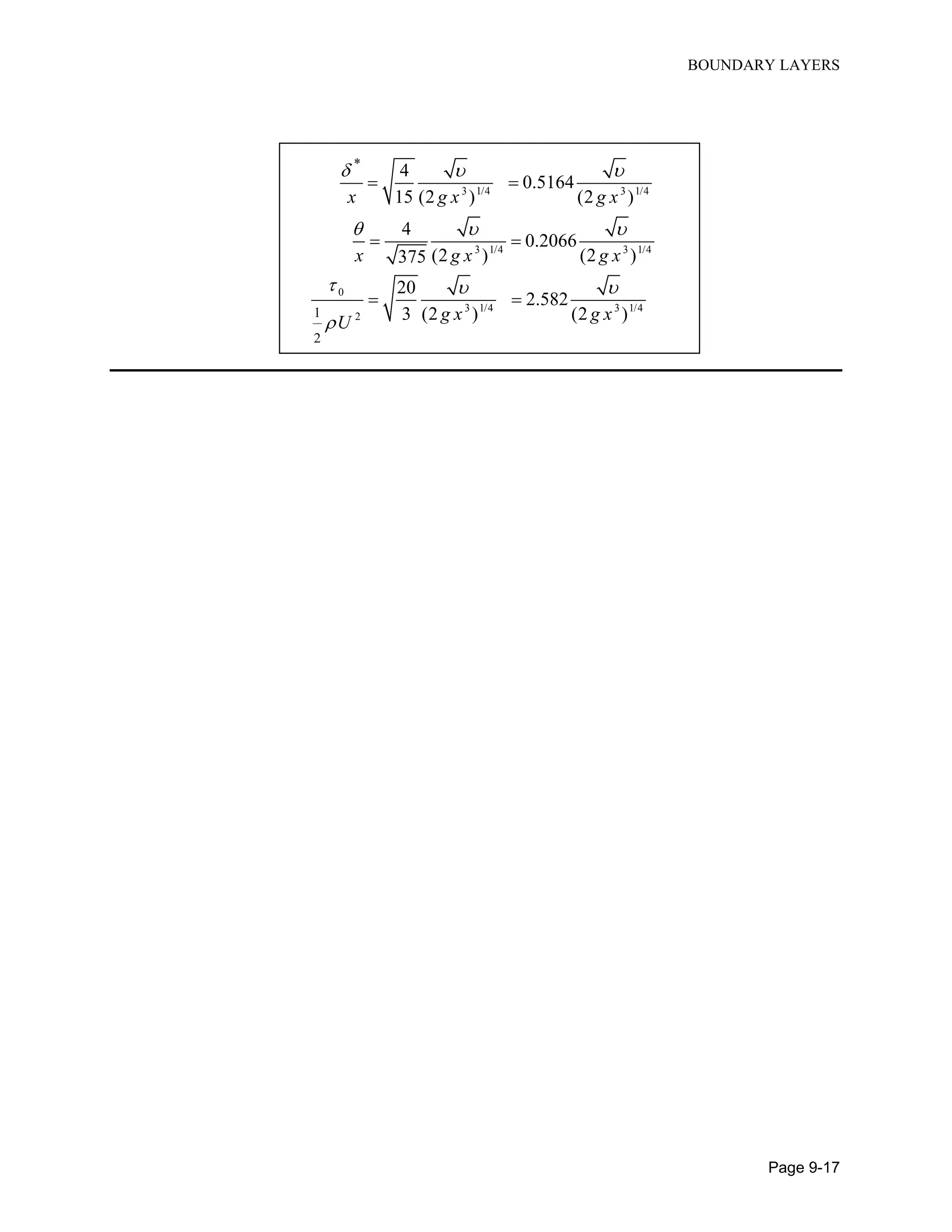
131. BUOYANCY-DRIVEN FLOWS
Page 10-1
Problem 10.1
From section 10.6 of the text, the partial differential equations to be satisfied are as follows:
1 1 1 1 1
(10.1.1)
(10.1.2)
R g
R R x R R R x R R R R R R R R
R
R x x R R R
     

    

             
                     
      
   
      
Using the given expressions, the following derivatives are obtained:
1
1
1 2
2
1
1 2
2
2 2
1 22
3
3 3
1 23
1
3
2 3
2
2 2
2 32
( )
[ ( ) ]
( )
m
m n
m n
m n
m n
r
r n
m n
C x n f m f
x
C C x f
y
C C x n f m n f
x y
C C x f
y
C C x f
y
C x n F r F
x
C C x F
y
C C x F
y













 






  





    
 







  







Substituting these expressions into Eqs. (10.1.1) and (10.1.2) and simplifying yields:
2 2 1 2 2 2 1
1 2 1 2
32 3 3
1 2 3
2
( 2 ) ( ) ( )
( ) (10.1.3)
m n m n
m n r n
m n C C x f mC C x f f f f
C
C C x f f f g x F
C
 
   
   
 
     
    
1 1
1 2 3 1 2 3 2 3 ( ) (10.1.4)m n r m n r r n
C C C x r f F mC C C x f F C C x F F       
     
If a similarity solution exists, all of the powers of x in Eq. (10.1.3) must be the same so that x
cancels out of the equation. This leads to the equations:
1 and 4 1m n r  

132. BUOYANCY-DRIVEN FLOWS
Page 10-2
Similarly, the powers of x in Eq. (10.1.4) must cancel. This produces the same two equations
for , andm n r . That is, for a similarity solution to exist:
1 and 4 1m n r  
In order to determine the values of , andm n r , we must impose the condition that the total
amount of heat leaving the source has the value Q. This condition is expressed by Eq. (10.26),
which requires that 0m r  so that the total amount of heat leaving the source is independent
of x . This additional condition leads to the following values for a similarity solution to exist:
1
2
1 1m n r   
Problem 10.2
For 1rP  , Eqs. (10.27a), (10.27b), (10.28a) and (10.28b) become:
0
1
(1 ) 0 (10.27 )
1
0 (10.27 )
(0) (0) (0) 0 (10.28 )
1
(10.28 )
2
d
f f f F a
d
F f F b
f f F a
f F d b

 




 
     
 
  
   
 
(a) Assume the following expressions to be valid for the functions andf F :
2
2
2 3
( )
1
( )
( )
f A
a
F B
a









For these assumed values, Eq. (10.27b) becomes:
2 4 2 4
6
0
( ) ( )
B AB
a a
 
 
  
 
It can be seen that this equation is satisfied by:
6A 
(b) Using 6A  in the expression for the function f , the following quantities are obtained:

133. BUOYANCY-DRIVEN FLOWS
Page 10-3
2
2 2 2
12 12
( ) ( )
f
a a
 
 
  
 
2 4
2 2 2 2 3
12 60 48
( ) ( ) ( )
f
a a a
 
  
   
  
3 5
2 2 2 3 2 4
3
2 2 2 3
144 432 288
( ) ( ) ( )
1 48 48
( ) ( )
f
a a a
d
f
d a a
  
  
 
   
    
  
 
    
  
Using these results, Eq. (10.28b) becomes:
2 30
1
12
( ) 2
d
a B
a
 
 



The value of the integral in this equation is 4
1/(8 )a , so that one equation relating the
constants anda B is:
3
(10.2.1)
3
a
B


Substituting the various derivatives evaluated above into Eq. (10.27a) yields the following
additional equation relating anda B:
96 (10.2.2)B a
From Eqs. (10.2.1) and (10.2.2) we get:
2
4 2
(4 2 )
3
a
B





Using these values, the solutions for the functions andf F become:
2
2
3
2 3
( ) 6
(4 2 )
(4 2 ) 1
( )
3 (4 2 )
f
F


 


  




It will be noted that these expressions satisfy the boundary condition defined by Eq.(10.28a).

134. BUOYANCY-DRIVEN FLOWS
Page 10-4
Problem 10.3
For 2rP  , Eqs. (10.27a), (10.27b), (10.28a) and (10.28b) become:
1
(1 ) 0 (10.27 )
d
f f f F a
d

 
 
     
 
0
2
0 (10.27 )
(0) (0) (0) 0 (10.28 )
1
(10.28 )
2
F f F b
f f F a
f F d b




  
   
 
Assume the following expressions to be valid for the functions andf F :
2
2
2 4
( )
1
( )
( )
f A
a
F B
a









For these assumed values, Eq. (10.27b) becomes:
2 5 2 5
8 2
0
( ) ( )
B AB
a a
 
 
  
 
It can be seen that this equation is satisfied by:
4 (10.3.1)A 
Using 4A  in the expression for f yields the following quantities:
3
2 2 2
2 4
2 2 2 2 3
3 5
2 2 2 3 2 4
3
2 2 2 3
8 8
( ) ( )
8 40 32
( ) ( ) ( )
96 288 192
( ) ( ) ( )
1 32 32
( ) ( )
f
a a
f
a a a
f
a a a
d
f
d a a
 
 
 
  
  
  
 
   
  
 
   
  
    
  
 
    
  
Using these results, Eq. (10.28b) assumes the following form:
2 50
1
12
( ) 2
d
a B
a
 
 



The value of the integral in the foregoing expression is 5
1/(10 )a , so that one of the equations
relating anda b is:

135. BUOYANCY-DRIVEN FLOWS
Page 10-5
45
(10.3.2)
8
B a


Substituting the various derivatives evaluated previously into Eq. (10.27a) yields the following
additional equation relating anda b :
2
64 (10.3.3)B a
From Eqs. (10.3.2) and (10.3.3) we get the values:
5
2
16
5
8
5
a
B




Using these values, we obtain the following solutions for the functions andf F :
2
2
5
2 4
4
( )
(16 2 / 5 )
8 1
( )
5 (16 2 / 5 )
f
F


 


 




It will be noted that these expressions satisfy the boundary condition defined by Eq.(10.28a).
Problem 10.4
(a) The assumed form of solution to Eq. (10.32a) is the following:
( ) i x
iU x A e


Substituting this assumed form of solution into Eq. (10.32a) leads to the result:
2 2 3 2
( ) 0i aR    
The solutions to this algebraic equation are as follows:
1/21/3
1/3
4
1 ( 1)
a
i
R
 

  
     
   
We note that the three cubic roots of (-1) are:
1/3 /3 5 /3
( 1) ; ;
(1 3)/ 2; 1; (1 3)/ 2
i i i
e e e
i i
  
 
   
Thus the values of the three exponent coefficients in the assumed form of solution consist of
one real root and one pair of complex conjugate roots. This makes the solution:

136. BUOYANCY-DRIVEN FLOWS
Page 10-6
1/21/3
1 4
1/21/3
2 4
1/21/3
3 4
1
2
1
2
1
1 (1 3)
1 (1 3)
a
a
a
R
R
i
R
i
 

 

 

  
    
   
  
     
   
  
     
   
(b) Applying the six boundary conditions defined by Eq. (10.32b) produces the following six
homogeneous equations that must be satisfied:
1 2 3 1 2 3
1 2 3
1 2 3 4 5 6
1 1 2 2 3 3 1 4 2 5 3 6
2 2 22 2 2 2 2 2
1 1 2 2 3 3
2 2 22 2 2 2 2 2
1 4 2 5 3 6
1 2 3 4 5 6
1 1 2 2 3 3 1 4
0
0
0 ( ) ( ) ( )
( ) ( ) ( )
0
0
C C C C C C
C C C C C C
C C C
C C C
C e C e C e C e C e C e
C e C e C e C e
     
   
     
     
     
   
  
  
     
      
     
     
     
     1 2 3
1 2 3
1 2 3
2 5 3 6
2 2 22 2 2 2 2 2
1 1 2 2 3 3
2 2 22 2 2 2 2 2
1 4 2 5 3 6
0 ( ) ( ) ( )
( ) ( ) ( )
C e C e
C e C e C e
C e C e C e
 
  
  
 
     
     
  
 
     
     
Setting the determinant of the coefficients of the constants 0iC  requires that the following
determinant be zero:

137. BUOYANCY-DRIVEN FLOWS
Page 10-7
1 2 3 1 2 3
1 2 3 1 2 3
1 2 3 1 2
1 2 3 1 2 3
2 2 2 2 2 22 2 2 2 2 2 2 2 2 2 2 2
1 2 3 1 2 3
1 2 3 1 2 3
2 2 2 2 2 22 2 2 2 2 2 2 2 2 2
1 2 3 1 2 3
1 1 1 1 1 1
( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) (
e e e e e e
e e e e e e
e e e e e
     
     
    
     
           
     
          
  
  
  
  
     
  
      32 2
) e


Problem 10.5
For free boundaries, as with rigid boundaries, two boundary conditions that must be satisfied are
that the perturbation velocity component in the x -direction and the perturbation temperature
should both be zero on the boundaries. However, the no-slip condition should be replaced with
the condition that there should be no shear stress on the free surfaces. With reference to
Appendix C, this implies that the following components of shear stress that act on the surface x
= constant should be zero:
0
u v w u
y x x z
      
   
   
Since u must be zero on all parts of the plane x = constant, it follows that derivatives of u
with respect to andy z will be zero. That is, the stress-free conditions expressed above may be
stated as follows:
0
v w
x x
  
 
 
Since the stability problem has been posed in terms of the velocity component in the x -direction
only, the foregoing conditions should be redefined in terms of the x -component of velocity.
This may be done by differentiating the continuity equation with respect to x , then imposing the
two conditions expressed above. This leads to the following condition:
2
2
2
0
or 0
u
x
D U





138. BUOYANCY-DRIVEN FLOWS
Page 10-8
Combining this last condition with the two unchanged conditions produces the following
boundary conditions that must be satisfied at the free surfaces:
2 2 2 2
( ) 0 ...on 0 and 1
x
U D U D U
h
    

139. 11
SHOCK WAVES

141. SHOCK WAVES
Page 11-1
Problem 11.1
The First Law of Thermodynamics may be expressed in the following form:
de dq pdv
but andh e pv dq T ds
hence ( )d h pv T ds p dv
Therefore T ds dh vdp
( , )
( , )
s s
s s p T ds dp dT
p T
h h
h h p T dh dp dT
p T
Substituting these expressions into the result obtained above gives:
s s h h
T dp dT dp dT vdp
p T p T
Equating the coefficients of anddT dp in this equation produces the following relations:
1
1
s h
T T T
s h
v
p T p
Differentiating the first of the above equations by p and the second by T permits s to be
eliminated to produce the following result:
2 2
2
1 1 1h h h v
v
T p T T p T p T T
h v
v T
p T
But, for an ideal gas we have 1/ /v RT p in which case the right side of this equation is
zero. That is:
0 ...for
h
p RT
p
This verifies that h is independent of p for an ideal gas, and that it depends on the temperature
T only for an ideal gas.

142. SHOCK WAVES
Page 11-2
Problem 11.2
( , )
( , )
s s
s s v T ds dv dT
v T
e e
e e v T de dv dT
v T
Substituting these expressions into the First Law of Thermodynamics gives:
s s e e
T dv dT dv dT p dv
v T v T
Equating the coefficients of anddT dv in this equation produces the following relations:
1
1
s e
T T T
s e
p
v T v
Differentiating the first of the above equations by v and the second by T permits s to be
eliminated to produce the following result:
2 2
2
1 1 1e e e p
p
T v T T v T v T T
e p
T p
v T
But, for an ideal gas we have p RT so that the right side of this equation is zero. That is:
0 ...for
e
p RT
v
This verifies that the internal energy e depends on the temperature T only for an ideal gas. A
much quicker way of arriving at this result is to use the reciprocity relation given at the end of
the Appendix on Thermodynamics.
0
e p
p T p T R
v T
if p RT .
Problem 11.3
From Appendix E we obtain the following two relations:
0
0
0 0 0
and
so
dq
s s dq de p dv
T
de p
dq dv
T T

143. SHOCK WAVES
Page 11-3
0
0 0
de p
s s dv
T T
0
0 0
i.e. v
dT
s s C Rvdv
T
Integrating this equation and using the fact that 1/ v yields the result:
0
0
0
log logv
T
s s C R
T
Using the relation p vC C R in the foregoing result produces the equation:
0
0
0
0 0 0
( )log log
log log
p
p
T
s s C R R
T
T T
C R
T T
Hence, using the ideal gas law, the last equation becomes:
0
0 0
log logp
T p
s s C R
T p
Problem 11.4
[ ( ) ]
where ( , ) and ( , )
u f x u a t
u u x t a a x t
( )
and 1
u u a
f u a t
t t t
u u a
f t
x x x
hence ( ) ( ) ( )
u u u u a a
u a u a u a t f
t x t x t x
But we know that u is a function of and that a is also a function of , so that we may
consider a to be a function of u only. Hence:
a da u
t du t
a da u
x du x
Substituting these results into the differential expression above gives:

144. SHOCK WAVES
Page 11-4
( ) ( ) 1
u u u u da
u a u a t f
t x t x du
( ) 1 1 0
u u da
u a t f
t x du
Either the first curly bracket is zero or the second curly bracket is zero. In general, the latter
cannot be true since the equation is valid for all values of the time t, so that the first curly bracket
must be zero. That is, the following is the solution to the wave equation:
( , ) [ ( ) ]u x t f x u a t
Problem 11.5
( ) 0
u u
u a
t x
( ) 0
u u u a u
u a
t x x x x x x
or
D u u a u
Dt x x x x
The partial derivative of a with respect to x may be shown to be proportional to the partial
derivative of u with respect to x as follows. In section 11.2, the following relationships were
established:
1
2
0
0
3 3
2 2
0 0 0
0 0 0
hence
1
2
1
2
a a
d
du a
a da d u
x d du x
a u
a x
u
x
Substituting this expression into the equation for the steepness of the wave front gives:
2
1
2
D u u
Dt x x

145. SHOCK WAVES
Page 11-5
Separating variables in the foregoing result produces the following equation:
2
1
2
u
D
x
Dt
u
x
Integrating this equation and taking the steepness to be when 0S t produces the following
value for the steepness at any time t :
1 1 1
2
t
u S
x
or
2 1 1
1
t
uS
x
This result gives the value of the time t to achieve any steepness
u
x
. In particular, to achieve
an infinite steepness:
2 1
1
t
S
This result shows that S must be negative if the steepness is to become infinite. That is, if a
shock wave is to form, the steepness of the original wave must be negative.
Problem 11.6
2
2 1
1 2
log
v
ps
C p
We now employ Eqs. (11.8b) and (11.8c) for the density ratio and the pressure ratio,
respectively, across a normal shock wave. This leads to the following expression:
2
2 1
1 2
1
( 1) 22
log 1 ( 1)
1 ( 1)v
Ms
M
C M
In the foregoing, we now want to express
2
1M in terms of
2
1( 1)M in the last square bracket.
Hence we rewrite the second square-bracketed term as follows:

146. SHOCK WAVES
Page 11-6
2
2 2 1
1 1
2 22
1 11
1
1 ( 1)
( 1) 2 ( 1)( 1) ( 1) 1
( 1) 1 ( 1)( 1) 1 ( 1)
M
M M
M MM
Then, denoting
2
1( 1)M by , the foregoing result assumes the following form:
2 1
log 1 log 1 log(1 )
1 1v
s
C
For 1, each of the foregoing logarithmic terms may be expanded as follows:
2 3
2 3
2 3
2 3
2 3
2 3
2 3
2 8
log 1 2 2
1 ( 1) ( 1) 3 ( 1)
1 ( 1) 1 ( 1) 1 ( 1)
log 1
1 ( 1) 2 ( 1) 3 ( 1)
1 1
log (1 )
2 3
Substituting these values into the expression derived above shows that the coefficients of the
terms that are linear and quadratic in are zero. Thus the leading non-zero term is:
2
3
3
2 ( 1)
3 ( 1)v
s
C
This result shows that weak shock waves, that is, waves for which 1 1M , are almost
isentropic.
Problem 11.7
(a) From the given pressure/density relation:
d dp
c
2
2 1
1
2 22
2 1 1 1 2 2
1
1
hence log ( )
( ) log
p p
c
p p c u u
In the last equation, the pressure difference has been eliminated using the momentum
equation, Eq. (11.3b). Dividing both sides of the last equation by c and using the fact that
the speed of sound is given by 2
/ /a dp d c yields the following identity:

147. SHOCK WAVES
Page 11-7
2 22
1 2
1
log (11.7.1)M M
Squaring Eq. (11.3a) and dividing the result by c gives:
2 2 2 2
1 1 2 2u u
c c
Using the results
2 2
1 1 2 2/ and /a c a c , where a is the speed of sound, yields the
following result from the last equation:
2
2 1
2
1 2
(11.7.2)
M
M
Substituting Eq. (11.7.2) into Eq. (11.7.1) results in the following equation:
2
2 21
1 22
2
log
M
M M
M
(b) From part (a) we have the result:
2 1
2
2 1
1
2
1
2
2
( )
2 2
2 1
( ) log
log
so that
p p
c
p p c
M
c
M
M M e
In the foregoing, Eq. (11.7.2) has been used. Substituting this equation into the main result
of part (a) produces the following expression:
2 1
2 1
2 ( )
2 21
1 12
2
( )
21 2
1
log
( )
1
p p
c
p p
c
M
M M e
M
p p
M e
c
1 2
2 1 2
1 ( )/
( ) /
1
p p c
p p c
M
e
Problem 11.8
From section 11.2, the continuity and momentum equations for a propagating sound wave are as
follows:

148. SHOCK WAVES
Page 11-8
( ) 0
1
u
t x
u u dp
u
t x d x
The corresponding equations for a shallow liquid are, from section 6.5:
( ) 0
h
hu
t x
u u h
u g
t x x
In the last two equations, h is interpreted as being the local depth of the liquid, not the mean
depth. Comparing the two sets of equations shows that the following variables are the analog of
each other:
Gas Liquid
u u
h
In order to make the analogy complete, the coefficients on the right side of the momentum
equation should be the same. This requires that:
0
0
1
1
but
dp
g
d
pp
c
dp
c
d
so that 2
c g
Then, in order to complete the analogy, we must have:
0
2
0
2 and 2
p
g
Problem 11.9
Using the given form of the solution, the following derivatives are obtained:

149. SHOCK WAVES
Page 11-9
u U p
x p x
u U
y y
u U p U p
c
t p t p x
v V p
y y x
Substituting these results into the continuity and momentum equations, and assuming that the
partial derivative of p with respect to x is not zero, leads to the following two equations to be
satisfied by andU V :
0
1
( ) 0
U V
p y
U U
U c V
p y
For the given form of similarity solution, the following derivatives are obtained:
1/2
1/2
1/2
*
*
*
1
2
U
p U
p
U dU
p
y dy
V dV
p
y dy
Substituting these results into the equations obtained above yields the following:
*
*
*
* * * *
1
0
2
1 1
( ) 0
2
dV
U
dy
dU
V U U C
dy
_____________________________________________________________________________

151. 12
ONE-DIMENSIONAL FLOWS

153. ONE-DIMENSIONAL FLOWS
Page 12-1
Problem 12.1
Using Eqs. (12.2a) and (12.2b) to evaluate the constant, the Riemann invariant along the line
constant  shows that in region 4 the value of the velocity and the value of the pressure must
satisfy the following relation:
1
0 0 0
1 1
(12.1.1)
pu p
a p p 
 
Similarly, using the   constant characteristic we get:
I
0 0 0
1 1uu p
a p a 
  
In the foregoing, Iu represents the gas velocity at, and of, the interface. In order to evaluate this
quantity, we consider the 1 characteristic which, using Eqs. (12.2a) and (12.2b) to evaluate the
constant, gives:
I 1
0 0
1 1u p
a p 
 
1
0 0 0
1 1 2
(12.1.2)
pu p
a p p  
  
Solving Eqs. (12.1.1) and (12.1.2) gives the following results for region 4:
1
0 0 0
1
1 1
pu p
a p p
 
    
 

154. ONE-DIMENSIONAL FLOWS
Page 12-2
Problem 12.2
(a) In general, the line separating regions 2 and 5 will have a different slope from the line that
separates regions 3 and 4 because the fluid temperatures are different. Noting that the time
taken for the reflected wave to travel the distance L is the same as that taken for the
transmitted wave to travel the distance (1 )L  , we have:
01 02
02
01
(1 )
1
L L
a a
a
a
 






Hence
2
02
2
01
(1 )T
T




(b) In regions 1 and 2, the velocity will be zero and the pressure will be 0p . Also, from Eqs.
(12.6a) and (12.6b), the velocity and the pressure in region 3 will be defined as follows:
3 3
01 01 0 01
1
u pU U
a a p a
  
In order to determine the velocity and pressure in regions 4 and 5, we consider a point ( , )P x t
that lies on the interface between regions 4 and 5. Then, by considering the two
characteristics that pass through this point, we get:

155. ONE-DIMENSIONAL FLOWS
Page 12-3
01 0 01
02 0
1 1
2
1 1
u p U
a p a
u p
a p
 
 
  
  
In the foregoing, the Riemann invariants have been evaluated from regions 3 and 2,
respectively. Solving these two equations for the velocity and the pressure that exist in
regions 4 and 5 gives:
4,5 01
01 01 02
4,5 01
0 01 02
2 /
(1 / )
2 /
1
(1 / )
u U a
a a a
p U a
p a a



 

(c) Using the foregoing expression for the pressure, the pressure differential across the
transmitted and reflected waves may be evaluated by subtracting the pressures in regions 2
and 3, respectively. This produces the following result:
01
0 02 01
02 01
0 01 02 01
2 /
( / 1)
( / 1)
2
( / 1)
t
r
p U a
p a a
p a aU
p a a a





 
 

Dividing the last two equations and simplifying gives the following result for the ratio of the
pressure differentials across the reflected and transmitted waves:
02
01
1
1
2
r
t
p a
p a
 
      
From part (a), this result may be expressed in terms of  only to give:
(1 2 )
2
r
t
p
p


 
 

Problem 12.3
Following the procedure employed in section 12.6 we may relate the problem to a stationary
shock wave by employing a Galilean transformation of magnitude 2nu to give:
1
2 1 2 2
2
( ) 1
n
n n n
n
u
u u u u
u
 
     
 

156. ONE-DIMENSIONAL FLOWS
Page 12-4
2
1
2 2 2
1 2
1 1
1
1
i.e.
1
1 1
2
n
p
p
u a M
p
p



  
   
            
In the foregoing equation, Eq. (11.4) has been used to evaluate the ratio of the gas velocities
across a normal shock wave, and the resulting expression has been simplified. Next, we use Eqs.
(11.8a) and (11.8c) to evaluate the Mach number in terms of the pressure ratio across the shock
wave.
21
1
2
2
2 1
1 1
1
1
2
1
2
n
n
n
M
M
M








and
2 1 2
1
1 1
1
1 1
2
n
p
M
p


 
    
 
1/2 1/2
1 2 2
2 2
1 1 1
1
1 1
2
n
p p
M a
p p



    
              

Substituting this last expression into the equation that was established for 2u gives:
2
1/2 1/2
1 11 2 2
2 2
1 1 1 1 2
1 1
1
1
1
1 1
2 1
1 1
2
p
pp p
u a
p p p
p

 


  
                                    
That is, the Mach number of the flow behind the shock wave will be described by the equation:
1/2
2 1 2 2
2
1 1 1 1 1
11
1 1 1
2
p p p
M
p p p

 

      
                  
Problem 12.4
From the definition of the Mach number, we introduce its variation, dM as follows:
2
2
1
2
u
M
RT
dM du dT
M u T


 
The temperature variation may be eliminated using Eq. (12.8c) to yield the following equation:
21 1
1
2 p
dM du q
M
M u C T
 

 
   
 

157. ONE-DIMENSIONAL FLOWS
Page 12-5
Next, we eliminate the velocity u from this equation by using Eq. (12.9a), in which dA and f
are taken to be zero. This gives the following result:
2
2
1
2( 1) p
dM M q
M M C T
  
   
The heat added, q , may be eliminated from the foregoing result using the relations given
involving the pressure variation and the heat added. This produces the following result:
2
2
1
2
dM M dp
M M p



 
Separating variables in the foregoing result and integrating gives:
2
2
log(1 ) log constant
(1 ) constant
M p
M p


   
 
Then the relationship between p and M at any two locations will be as follows:
2
2 1
2
1 2
1
1
p M
p M





Problem 12.5
From the definitions of the Mach number and the speed of sound we have the result:
1/2 1/2
1 1 2 2 2 2 1
2 2 1 1 1 1 2
M u a T p T
M u a T p T


   
        
   
In the foregoing, the velocity ratio has been eliminated using the continuity equation, and the
density ratio has been eliminated using the ideal gas law. Solving this equation for the
temperature ratio and using the result of Prob. 12.4 to evaluate the pressure ratio, yields the
result:
22 2
2 2 2
2
1 1 1
1
1
T M M
T M M


   
         
To obtain an expression for the density ratio we use the ideal gas law as follows:
2 2 1
1 1 2
p T
p T




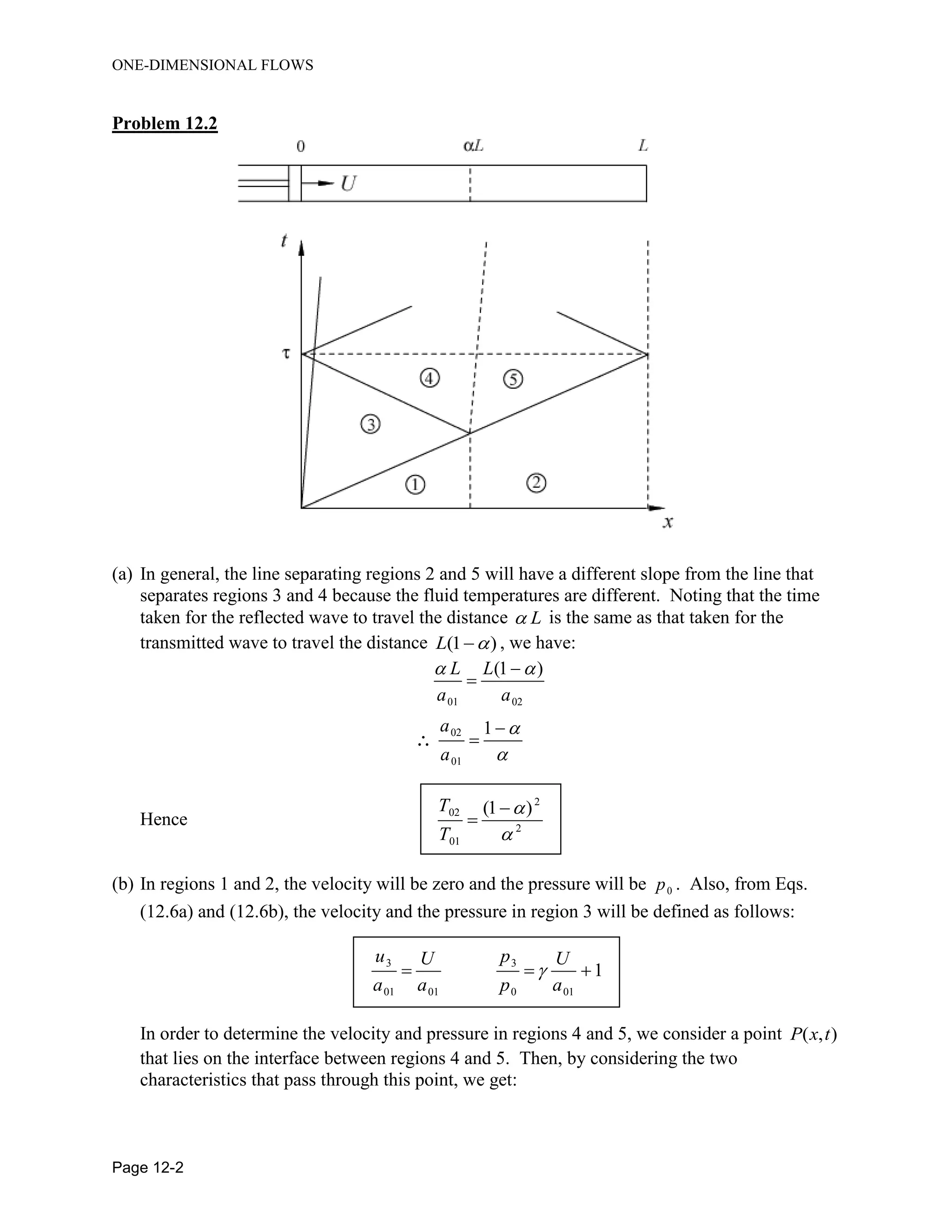
158. ONE-DIMENSIONAL FLOWS
Page 12-6
Using the result of Prob. 12.4, and the result obtained above, yields the following expression:
32 2
2 1 1
2
1 2 2
1
1
M M
M M
 
 
   
         
Problem 12.6
Starting with the ideal gas law and employing the given expression for h , we get:
p
R
p RT h
C
  
Substituting this result into the given expression for the entropy rise produces the result:
1 1 1
1
1 1
log log
v p
s s p R h
C p p C
 

 
  
     
             
In order to eliminate  , we use the energy equation and the continuity equation as follows:
2
0
2
0
1/2
0
2
1
2
1
[2( )]
u
h h
m
h h
A
A
h h
m


 
 
  
 
 
Substituting this result into our expression for the entropy change yields the result:
1
2 2
1 1
02
1
2
log ( )
v p
s s R A
h h h
C p C m




 
   
   
  
 
Separating the variable and the constant components of the last equation gives the result:
1
1 2 2
1 12
0 2
1
2
log ( ) log
v p
s s R A
h h h
C p C m




  
     
       
    
 
The maximum value of the entropy s will occur when the derivative of the right side of the last
equation, with respect to h , is zero. This requires the following:
1 3
2 2
0 01
2
0
1 1
( ) ( ) 0
2
( )
h h h h h
h h h
 

 

 
    
 
Simplifying this expression shows that it follows that:

159. ONE-DIMENSIONAL FLOWS
Page 12-7
0 0
1 1
or
2 2
h h T T
  
 
i.e. 21 1
1
2 2
T M T
   
  
 
In the last equality, the stagnation temperature has been evaluated using Eq. (12.10a). Then:
maximum 1s M  
Problem 12.7
As in Prob. 12.6, we rewrite the expression for the entropy change as follows:
1 1
1
1
1 1
1
1
log
i.e. log log (12.7.1)
v p
v p
s s R h
C p C
s s h R
C p C










 
  
 
 
   
         
But from the momentum equation we get:
2
0
2
02
p
u p p
m R
h p
A C



 
 
i.e.
2
0
2 2
1
(12.7.2)
p pC p m C
h
R A R 
  
      
   
In order to obtain Eq. (12.7.2), the velocity has been eliminated through use of the continuity
equation and the pressure has been eliminated through use of the ideal gas law. In principle Eq.
(12.7.2) can be solved for the density  and the result substituted into Eq. (12.7.1) to give an
explicit expression for the entropy change in terms of the enthalpy h . However, the solution is
more compact if it is kept in the form of the two parametric equations of the form ( )s s  and
( )h h  . Then, by substituting Eq. (12.7.2) into Eq. (12.7.1), we get the following result:
2
0 1
0 2
1
2
0 2
1 1
log log
1 1
v
p
s s m
p
C A p
C m
h p
R A



 
 
      
               
    
     
    
For brevity we introduce the following notation:

160. ONE-DIMENSIONAL FLOWS
Page 12-8
1 p
v
s s Cm
S Q G
C A R

   
Then the equations that define the Rayleigh line become:
2
1
0
1
2
0
1
log log
Q
S p
p
G Q
h p



 
 
    
              
 
  
 
The derivatives of the entropy change and the enthalpy, with respect to the density, are:
2
0
2
0
2
02
( 1)
( )
2
Q
p
d S
d Q
p
dh G Q
p
d
 




  
 
  
   
 
 
 
 
   
 
Then, eliminating d from these two equations and noting that 2
0( )p Q p  from the
momentum equation, we get the following expression for the derivative of the entropy with
respect to the enthalpy:
2
2
( )
(12.7.3)
Q
p
d S
dh Q
G p p



 
 
  
 
 
 
The entropy reaches a maximum when the numerator of Eq. (12.7.3) is zero; that is, when:
2
Q
p


Then, since 2 2 2
/Q u  and 2
/a p  , this result reduces to the following condition:
maximum 1S M  
The enthalpy will reach a maximum when the denominator of Eq. (12.7.3) is zero; then:
2
Q
p


Then, since 2 2 2
/Q u  and 2
/a p  , this result reduces to the following condition:
maximum 1/h M   

161. 13
MULTI-DIMENSIONAL FLOWS

163. MULTI-DIMENSIONAL FLOWS
Page 13-1
Problem 13.1
The differential equation governing three-dimensional, unsteady, irrotational flow is given by
Eq. (13.1). For steady two-dimensional flow this equation reduces to the following form:
2 2
2 2 2
2
2 2 2 2
2 2 2
2 2 2
2 2
2 2 2
1
( )
1
1
1
2
x y
x y
x y a
u v
a x y x y
u v v u
a x x y y x y
u u v v
a x x y y
u u
u e e
u e e
Thus the differential equation governing the velocity potential for this class of flows is:
2 2 2 2 2
2 2 2 2 2
1 2 1 0
u u v v
a x a x y a y
Problem 13.2
For two-dimensional, steady flow, the continuity equation is:
( ) ( ) 0u v
x y
Substituting the given expressions into the left hand side (LHS) of this equation shows that:
0 0LHS
0 ...as required
x y y x
( ) ( ) 0 ...for all ( , )u v x y
x y
From the condition of irrotationality we get:
0
v u
x y
Multiplying this equation by the density gives the result:
0
v u
x y
( ) ( ) 0v u v u
x y x y

164. MULTI-DIMENSIONAL FLOWS
Page 13-2
2 2
2 2
0 0
i.e. 0
v u
x y x y
In the last equation, use has been made of the definition of the stream function. The last two
terms in the last equation may be eliminated by use of the momentum equations in the form:
2
2
u u p
u v a
x y x
v v p
u v a
x y y
Using the last two equations to eliminate the derivatives of the density gives the result:
2 2 2 2
2 2 2 2 2 2
0 0 0 0
2 2 2 2 2 2 2
2 2 2 2 2 2 2
0
2 0
uv u v u u v uv v
x y a x a y a x a x
uv u v
x y a x y a x a y
In arriving at the last result, each of the four terms in the previous equation was treated in the
following manner:
2 2
0 0
2
02 2
0
1
( )
1
uv u uv
u u
a x a x x
u v
u
a x x
The second term inside each square bracket cancel each other, yielding the result:
2 2 2 2 2
2 2 2 2 2
1 2 1 0
u u v v
a x a x y a y
Problem 13.3
(a) Consider both the velocity potential and the stream function to be functions of andx y , and
consider infinitesimal changes in both andx y . Then the total change in the velocity
potential and the stream function will be given by the following expressions:
0 0
0 0
cos sin
sin cos
d dx dy u dx vdy
x y
q dx q dy
d dx dy vdx u dy
x y
q dx q dy
That is, the total changes in the velocity potential and the stream function are:

165. MULTI-DIMENSIONAL FLOWS
Page 13-3
0
(cos sin )
( sin cos )
d q dx dy
d q dx dy
From the foregoing two equations, the following identities are obtained:
2
0 0 0
2
0 0
cos cos sin cos
sin sin sin cos
d q dx q dy
d q dx q dy
Subtracting these two equations yields an expression for dx . A similar procedure leads to an
analogous expression for dy . The resulting expressions are:
0
0
cos sin
sin cos
dx d d
q q
dy d d
q q
(b) Since both the velocity potential and the stream function are considered to be functions of
andq , we have the equations:
d d
d dq d
dq d
d d
d dq d
dq d
Substituting these expressions into the equations obtained above gives the following
equations for the variation in andx y with respect to andq :
0 0
0 0
cos sin cos sin
sin cos sin cos
dx dq d
q q q q q q
dy dq d
q q q q q q
(c) We now consider andx y to be functions of andq . Then from differential calculus:
x x
dx dq
q
y y
dy dq
q
Then, equating the coefficients of anddq d in the expressions above with those obtained in
(b), leads to the following equalities:

166. MULTI-DIMENSIONAL FLOWS
Page 13-4
0
0
0
0
cos sin
cos sin
sin cos
sin cos
x
q q q q q
x
q q
y
q q q q q
y
q q
(d) Using the first two results obtained above, we form the second mixed derivative of x , then
the last two results are used to form the second mixed derivative of y . This produces the
following expressions:
2
0
0 0
2 2
2
0
0 0
2 2
sin cos
cos sin sin
cos sin
sin cos cos
x
q q q q q
d
q q dq q
y
q q q q q
d
q q dq q
We next add the two mixed second derivatives as follows:
2 2
0 0
2
0
1
sin cos
1 1
1
x y
q q q q
d
q q dq
d
dq q
Equating the first and third equalities on the right side of the foregoing equations gives:
01d
q
q dq q
Adding the same two equations again, but in a different manner, yields the result:
2 2
0
2
1 1
cos sin
x y
q q q q q
Equating the last two equalities in the foregoing equations produces the result:

167. MULTI-DIMENSIONAL FLOWS
Page 13-5
0
q
q
(e) Bernoulli’s equation for the case under consideration is:
21
contant
2
dp
q
0
so that
dp
q dq
dp
q
dq
The following identity is now obtained:
0 0 0
2 2
d d d dp
dq dq dp dq
We now use the definition of the speed of sound and the last two equations to give:
0 0
2
d q
dq a
From part (d) we have the following result:
0
0 0
1
1
d
q
q dq q
d
dq q
Using the expression for the derivative of the density ratio in the last equation produces the
following result:
0 21
(1 )M
q q
Differentiating the last result with respect to yields:
2 2
0 2
2
1
(1 )M
q q
Another expression for the same quantity may be obtained from a result obtained in (d) as
follows:
0
q
q
2 2
0 0 0
2
q q
q q q q q

168. MULTI-DIMENSIONAL FLOWS
Page 13-6
2 2
0 0 02
2
i.e. M q
q q q q
In the last identity, the result obtained above for the derivative of the density ratio with
respect to the velocity q has been used. Equating the two expressions for the second mixed
derivative of the velocity potential , then simplifying, produces our final result:
2 2
2 2 2
2 2
(1 ) (1 ) 0q q M M
q q
Problem 13.4
From section 13.2 of the text, the general form of the Janzen-Rayleigh expansion equation is as
follows:
22 2
2 2 2 2 2
2
n n n nn n n n
n n n ni i i j i j
a
M M M M M
x x a x x x x
2
2
2 2
2
2
2 20 0 1
1
where 1 1
2
1
1 1 ( 1)
2
n
n i
i i i
a
M M
xa
M M
x x x
The ratio of the two speeds of sound has to be inverted prior to substitution into the governing
equation. This may be done by considering the required ratio to be of the following form:
2
1 2
2
(1 ) 1
a
a
Hence the required form of the ratio of the speeds of sound is found to be:
22 22
2 40 0 0 1
2
1 1
1 1 ( 1) 1 4
2 4i i i i
a
M M
a x x x x
Also, the product of the three round-bracketed terms in the governing equation is:
2 4 2 40 1 2 0 1 2
2 2 2
2 40 1 2
i i i j j j
i j i j i j
M M M M
x x x x x x
M M
x x x x x x
That is:

169. MULTI-DIMENSIONAL FLOWS
Page 13-7
2 2 2 2
0 0 0 1 0 0 0 1 0 0 0 1 2
2 2 2
1 1 0 1 0 1 0 1 1
2
i j i j i j i j i j i j i j i j
i j i j i j i j i j i j
M
x x x x x x x x x x x x x x x x
x x x x x x x x x x x x
x
2 2 2
40 0 0 2 0 0 0 2
i j i j i j i j i j i j
M
x x x x x x x x x x x
The right side of the governing equation is evaluated by multiplying the two expansions obtained
above with the square of the Mach number at infinity. This gives the following result for 3 :
22
2 2
3 0 0 1 0 0 0
2
2 2 2
0 1 0 0 0 1 0 0 0 1
1
( 1) 1 4
4
1
1
2
i i i i i i j i j
i i j i j i j i j i j i j
x x x x x x x x x
x x x x x x x x x x x x x
2 2 2
1 1 0 1 0 1 0 1 1
2 2 2
2 0 0 0 2 0 0 0 2
i j i j i j i j i j i j
i j i j i j i j i j i j
x x x x x x x x x x x x
x x x x x x x x x x x x
Problem 13.5
The exact version of the pressure coefficient is given by Eq. (13.4a), which is:
/( 1)
2
2 2
2 1
1 ( ) 1
2
pC U
M a
u u
where 2 2 2 2
2 ( ) ( ) ( )U U u u v wu u
/( 1)
2 2 2
2 2
2 1
1 (2 ( ) ( ) ( ) 1
2
pC U u u v w
M a
The quantity inside the square brackets is of the following form:
2( 1)
(1 ) 1
2!
n n n
where 2
( 1)
so that
1 2! 2( 1)
n n
n

170. MULTI-DIMENSIONAL FLOWS
Page 13-8
2 2 2 2 2
2 2 2
2
(2 ( ) ( ) ( ) [4 ( ) ]
2 8
pC U u u v w U u
M a a
Simplifying this expression yields the following equation which is valid to the second order in
the primed (i.e. small) quantities:
2 2
2
( ) ( )
2p
u u v
C
U U
Problem 13.6
The drag force that acts on one wave-length of wall is defined by the following integral:
0
0
( ,0)
2 2
( ,0)cos
D
dy
F p x dx
dx
x
p x dx
In the foregoing equation, ( ,0)p x is the pressure difference across the wavy wall, and the
sinusoidal variation of the wall height has been employed. It will be assumed that the pressure
below the wall surface is the same as the reference pressure far from the wall. For subsonic flow
the pressure coefficient is given by Eq. (13.6b). Hence the required pressure distribution will be
defined as follows:
22
1
2
4 / 2
( , ) sin
1
M y
p
x
C x y e
M
2
2
2 / 2
( ,0) sin
1
U x
p x
M
Thus for subsonic flow the drag force per unit wavelength of wall will be:
2 2
2 0
2 2 2
sin cos
1
D
U x x
F dx
M
i.e. 0 for 1DF M
For supersonic flow the pressure coefficient is defined by Eq. (13.7b). Hence the required
pressure distribution will be defined as follows:
2
2
4 / 2
( , ) cos 1
1
p
x
C x y x M y
M
2
2
2 / 2
( ,0) cos
1
U x
p x
M
Thus for supersonic flow the drag force per unit wavelength of wall will be:

171. MULTI-DIMENSIONAL FLOWS
Page 13-9
2 2 2
2
2 0
2 2
cos
1
D
U x
F dx
M
2 2 2
2
2
i.e. 1
1
D
U
F for M
M
Problem 13.7
Considering the boundary condition at r a , the solution for the velocity potential will be of the
following separable form:
2
( , ) ( )cos
x
x r R r
Substituting this expression into the differential equation gives:
22
22 2
2
2
(1 ) 0
d R dR
r r M r R
dr dr
This is the modified Bessel equation of order zero whose solution is:
2
0
2
( ) 1
r
R r AI M
In the foregoing, 0I is the modified Bessel function of the first kind of order zero. The second
solution has been suppressed because it contains a logarithmic term – which is physically
unacceptable. Then the solution for the velocity potential becomes:
2
0
2 2
( , ) 1 cos
r x
x r AI M
Imposing the boundary condition at r a and using the result 0 1( ) ( )I x I x gives:
2 2
1
1
21 1
U
A
aM I M
Then the velocity potential for the flow field will be:
2
0
2 2
1
2
1
2
( , ) cos
21 1
r
I M
U x
x r
aM I M
Using this result, and Eq. (13.4b), the following expression is obtained for the surface pressure
coefficient on the cylinder:

172. MULTI-DIMENSIONAL FLOWS
Page 13-10
2
0
cylinder 2 2
1
2
1
4 / 2
sin
21 1
p
a
I M
x
C
aM I M
For a plane wall, the pressure coefficient is given by Eq. (13.6b). Thus the surface pressure
coefficient will be given by the following expression:
plane 2
4 / 2
sin
1
p
x
C
M
Thus it follows that the ratio of the two surface pressure coefficients is:
2
0
cylinder
2
plane 1
2
1
2
1
p
p
a
I MC
aC I M
For large values of the argument x , the following asymptotic expansions apply:
0
1
0
1
1
( ) 1
82
3
( ) 1
82
( ) 1 3
1 1
( ) 8 8
1
1
4
x
x
e
I x
xx
e
I x
xx
I x
I x x x
x
Then the ratio of the surface pressure coefficients for large values of the cylinder-radius/surface-
wavelength ratio becomes:
cylinder
2
plane
1
1
81
p
p
C
aC M
This result shows the initial effect of surface curvature on the surface pressure coefficient.
___________________________________________________________________________
Problem 13.8
The drag coefficient, according to Ackeret's linear theory, is given by Eq. (13.9b). Then for zero
angle of attack, and for no camber, the drag coefficient will be given by the following
expression:

173. MULTI-DIMENSIONAL FLOWS
Page 13-11
2
2
2 0
4
( )
1
c
D
c
C dx
M
For the wing section shown, the half-thickness function is defined as follows:
for 0 / 2
( )
1 for / 2
x
x c
c
x
x
c x c
c
Then the drag coefficient will have the following value:
2
/ 2
2 2
2 0 / 2
4
(1/ ) ( 1/ )
1
c c
D
c
c
C c dx c dx
M
2
2
4
1
DC
M
___________________________________________________________________________
Problem 13.9
Dividing the given equation for the upper surface of the airfoil by 2
a we get:
22 2
2
1
1 1
2 2
c c
x
a a a
2
2
1
1 2 1
2
c c
x
a a a
In the foregoing, the radius a has been taken to be large compared with both the half-thickness
of the wing and the chord. This linearization is required since Ackeret's theory is a linear theory,
and consistency requires that the equation of the surface be linearized. Solving the last equation
for the half-thickness produces the result:
2
1
2 2 2
c c
x
a
The radius a may now be eliminated from this result by noting that 0 when 0x . This
produces the following identity, which may be used to eliminate a :
2
0
2 8
2
2 2
c c
a
c c
x
c
Thus the half-thickness function will be defined by the following expression:

174. MULTI-DIMENSIONAL FLOWS
Page 13-12
2
2
1 2
( )
2 2
c
x x
c
2
4
( )
2
c
x x
c
Then, according to Ackeret's theory, the drag coefficient will be defined as follows:
22
42 0
4 16
21
c
D
c c
C x dx
cM
2
2
16
3 1
DC
M
Comparing this result with that obtained in Prob. 13.8 shows that the smooth-contour airfoil has
a larger drag than that of the sharp-edged airfoil in supersonic flow, and that the ratio of the two
drags is 4/3.
___________________________________________________________________________

175. 14
SOME USEFUL METHODS OF ANALYSIS

177. SOME USEFUL METHODS OF ANALYSIS
Page 14-1
Problem 14.1
The function is periodic in the range –L ≤ x ≤ L and it is odd in x. Hence we use Eqs. (14.4a) and
(14.4b):
1
( ) sinn
n
n x
f x b
L


 
0
2
where ( ) sin
L
n
n x
b f x dx
L L

 
But over the range 0 ≤ x ≤ L we have f (x) = H, so that;
0
2
sin
L
n
n x
b H dx
L L

 
0
2
cos
L
H L n x
L n L


 
   
 2
1 ( 1)nH
n
  
 
1
2
( ) 1 ( 1) sinn
n
n x
f x H
n L




  
_____________________________________________________________________________
Problem 14.2
The function is periodic in the range –L ≤ x ≤ L and it is even in x. Hence we use Eqs. (14.2a),
(14.2b) and (14.2c):
0
1
( ) cosn
n
n x
f x a a
L


  
0
0
1
where ( )
L
a f x dx
L
 
0
2
and ( ) cos
L
n
n x
a f x dx
L L

 
But over the range 0 ≤ x ≤ L we have f (x) = H x2
/L2
, so that;
2
0 20
2
3
L x H
a H dx
L L
 
and
0
2
cos
L
n
n x
a H dx
L L

 
2
3 3 0
2
cos
nH
d
n

  

 
2 2
4
( 1)nH
n 
 
2 2
1
4
( ) ( 1) cos
3
n
n
H n x
f x H
n L




  
_____________________________________________________________________________

178. SOME USEFUL METHODS OF ANALYSIS
Page 14-2
Problem 14.3
The function is periodic in the range –L ≤ x ≤ L and it is odd in x. Hence we use Eqs. (14.4a) and
(14.4b):
1
( ) sinn
n
n x
f x b
L



0
2
where ( ) sin
L
n
n x
b f x dx
L L

 
But over the range 0 ≤ x ≤ L we have f (x) = H x2
/L2
, so that;
2
20
2
sin
L
n
x n x
b H dx
L L L

 
2
3 3 0
2
sin
nH
d
n

  

 
1
3 3
2 4
( 1) 1 ( 1)n nH H
n n 

      
1
3 3
1
2 4
( ) ( 1) 1 ( 1) sinn n
n
n x
f x H
n n L

 



 
       
 

_____________________________________________________________________________
Problem 14.4
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
f(x)/H
x/L
10 Terms
20 Terms
30 Terms

179. SOME USEFUL METHODS OF ANALYSIS
Page 14-3
The graph shown above was drawn using EXCEL. Each curve on the graph was generated using
the number of terms specified, and for increments of 0.01 for x/L.
_____________________________________________________________________________
Problem 14.5
(a)
2 4
cos 1
2! 4!
z z
z     
Therefore 3 3
cos 1 1 1
2! 4!
z z
z z z
    
Hence 1
1
2
b   pole of order 3 at z = 0
(b)
2 4
cosh 1
2! 4!
z z
z     
Therefore 3 3
cosh 1 1 1
2! 4!
z z
z z z
    
Hence 1
1
2
b  pole of order 3 at z = 0
(c) Here the singularity is at z = α so that our expansion should be about the point z = α.
2 3
( ) ( )
{ } {1 ( ) }
2! 3!
z z z z
e e e e z    
  
       
Therefore 2 2
1 1 1 ( )
( ) ( ) ( ) 2! 3!
z
e z
e
z z z
 
  
 
      
   
Hence 1b e
 pole of order 2 at z = α.
__________________________________________________________________________
Problem 14.6
(a) There is a pole of order 3 at z = 0 here so that from Eq. (14.12b)
2
3
1 2 30
1 cos
lim
2!z
d z
b z
dz z
 
   
  
0
1
lim ( cos )
2z
z

 
  
 
Hence 1
1
2
b  
(b) There is a pole of order 3 at z = 0 here so that from Eq. (14.12b)

180. SOME USEFUL METHODS OF ANALYSIS
Page 14-4
2
3
1 2 30
1 cosh
lim
2!z
d z
b z
dz z
 
   
  
0
1
lim (cosh )
2z
z

 
  
 
Hence 1
1
2
b 
(c) There is a pole of order 2 at z = α here so that from Eq. (14.12b)
2
1 2
lim ( )
( )
z
z
d e
b z
dz z


 
   
  
 lim z
z
e


Hence 1b e

__________________________________________________________________________
Problem 14.7
(a) let cos and sinp z q z 
This function is singular at z = 0. Then from Eq. (14.12c);
1
0
( 0) cos
( 0) cos z
p z z
b
q' z z 

 

Hence 1 1b 
(b) let and sinh( )p z q z   
This function is singular at z = α. Then from Eq. (14.12c);
1
( )
( ) cosh( ) z
p z z
b
q' z z 

  

 
 
Hence 1b 
(c) ) let and ( )z
p e q z   
This function is singular at z = α. Then from Eq. (14.12c);
1
( )
( ) 1
z
z
p z e
b
q' z 

 

 

Hence 1b e

__________________________________________________________________________

181. SOME USEFUL METHODS OF ANALYSIS
Page 14-5
Problem 14.8
There are poles of order 2 at z = +α and at z = −α, as can be readily seen by rewriting the given
function as follows;
2 2
2 2 2 2 2
4 4
( )
( ) ( ) ( )
F z
z z z
 
  
 
  
Then we can use Eq. (14.12c) at both singularities using m = 2.
2 2
2 3
4 8
Residue lim lim
( ) ( )z z z
d
dz z z  
 
   
    
           
1
Residue z 

 
2 2
2 3
4 8
Residue lim lim
( ) ( )z z z
d
dz z z  
 
   
    
           
1
Residue z 


_____________________________________________________________________________
Problem 14.9
(a) Step 1: sin
x
A
L

Step 2:
sinh ( )
sinh
H y
L
H
L



Step 3:
sinh ( )
( , ) sin
sinh
H y
x LT x y A
HL
L





(b) Step 1: sin
x
B
L

Step 2:
sinh
sinh
y
L
H
L


Step 3:
sinh
( , ) sin
sinh
y
x LT x y B
HL
L




__________________________________________________________________________

182. SOME USEFUL METHODS OF ANALYSIS
Page 14-6
Problem 14.10
(a) Step 1: sin
y
C
H

Step 2:
sinh ( )
sinh
L x
H
L
H



Step 3:
sinh ( )
( , ) sin
sinh
L x
y HT x y C
LH
H





(b) Step 1: sin
y
D
H

Step 2:
sinh
sinh
x
H
L
H


Step 3:
sinh
( , ) sin
sinh
x
y HT x y D
LH
H




__________________________________________________________________________
Problem 14.11
Using the principle of superposition, we obtain the required solution by superimposing the
results of Probs. (14.9) and (14.10).
sinh ( ) sinh
( , ) sin sin
sinh sinh
sinh ( ) sinh
sin sin
sinh sinh
H y y
x xL LT x y A B
H HL L
L L
L x x
y yH HC D
L LH H
H H
 
 
 
 
 
 

 

 
If the boundary conditions on all four sides were different graphical functions, we would
represent each of them by their Fourier series and the solution would be the sum of four different
series.
_____________________________________________________________________________

183. SOME USEFUL METHODS OF ANALYSIS
Page 14-7
Problem 14.12
The y component of the solution will be;
sin
y
U
h

The t component of the solution will be exponential with the coefficient of t being the product of
υ with the square of the quantity π/h. That is, the t component of the solution will be;
2
( / )h t
e  
Thus the complete solution will be;
2
( / )
( , ) sin h ty
u y t U e
h
  

_____________________________________________________________________________
Problem 14.13
22
2
1 1
0
2
d F dF f dF
df F df F df

  
 
(a) Let F = aF * and f = bf *. Then the differential equation above becomes;
22
2 2 2
1 1
0
2
a d F a dF f dF
b d f b F d f F d f
   
    

  
 
If the equation is to be invariant, we must have;
2 2
2 2 2
1 1
a F f F F
b F f f f
 
 

    
 
That is 2
F
f
  is an invariant coordinate.
(b) Let ( ) n dF
G f
df
  be the new dependent variable
And 2
f F 
 be the new independent variable
We will choose n later so that f is eliminated from the differential equation.
The following derivatives are now obtained for substitution into the differential equation:
ndF
f G
df


2
( 1)
2
n nd F d dG
n f G f
df df d


   
   
 
(*)
But 2 3 2
( ) 2
d d dF
f F f F f
df df df
   
   
1 ( 2)
2 n
f f G  
  
In the above we have used the definitions of G and ξ to eliminate F in favor of ξ and f.
Substituting this result into Eq. (*) gives;

184. SOME USEFUL METHODS OF ANALYSIS
Page 14-8
 
2
( 1) 1 ( 2)
2
( 1) ( 1) 2( 1)
2
2
n n n
n n n
d F dG
n f G f f f G
df d
dG dG
n f G f f G
d d



 
     
     
    
   
Substituting the above derivatives into the differential equation yields the result;
2
( 1) ( 1) 2( 1) 2( 1) ( 1)1
2 0
2
n n n n ndG dG G G
n f G f f G f f
d d

   
          
      
 
We now note that this will be an ODE for ( )G  if we choose 1n   . Then the ODE is;
2
2 0
2
dG dG G G
G G
d d

   
    
That is
(2 2 1)
2 ( 2 )
dG G G
d G

  
 
 

Once this equation is solved for ( )G  , we can integrate the following equation to get ( )F f ;
dF
f G
df

Once the equation above is solved for ( )F f , we can integrate the following equation to get
( )f  ;
d f
F
d

That is, the problem has been reduced to a series of first order equations, for which many
analytical and numerical methods of solution exist.
_____________________________________________________________________________

186. K15081
9 781466 516960